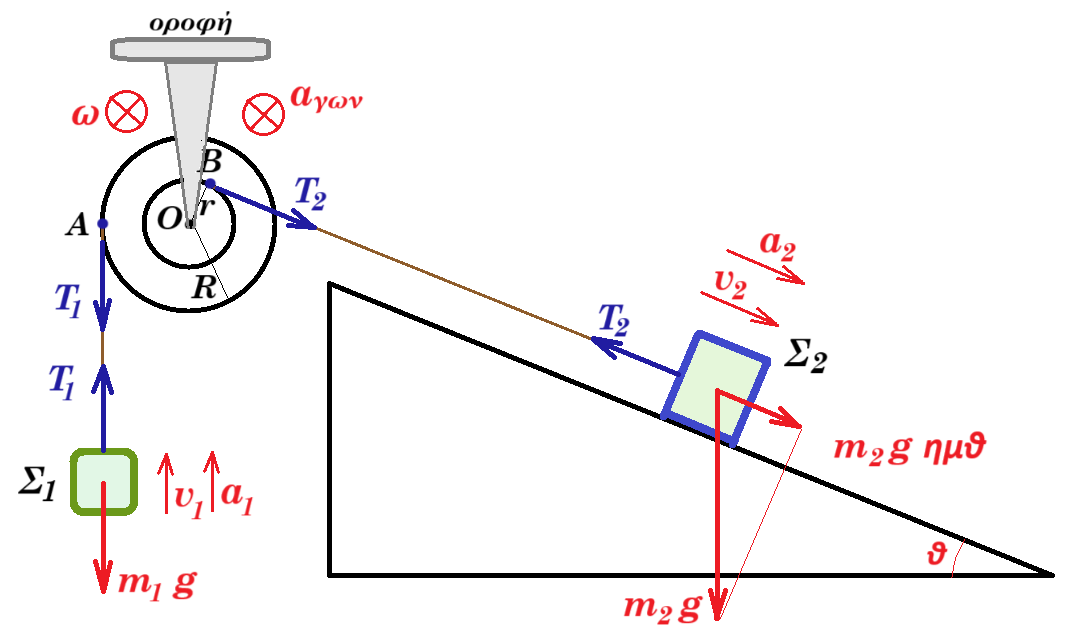

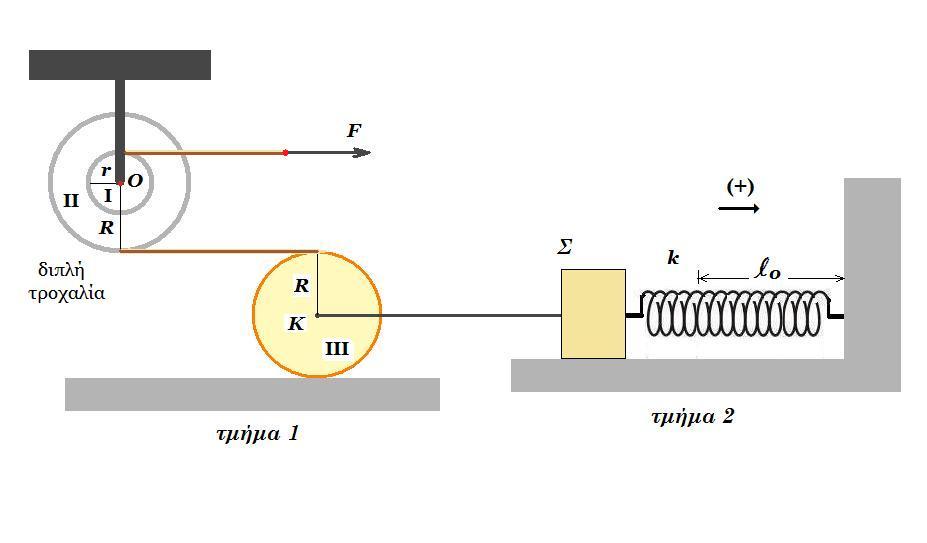
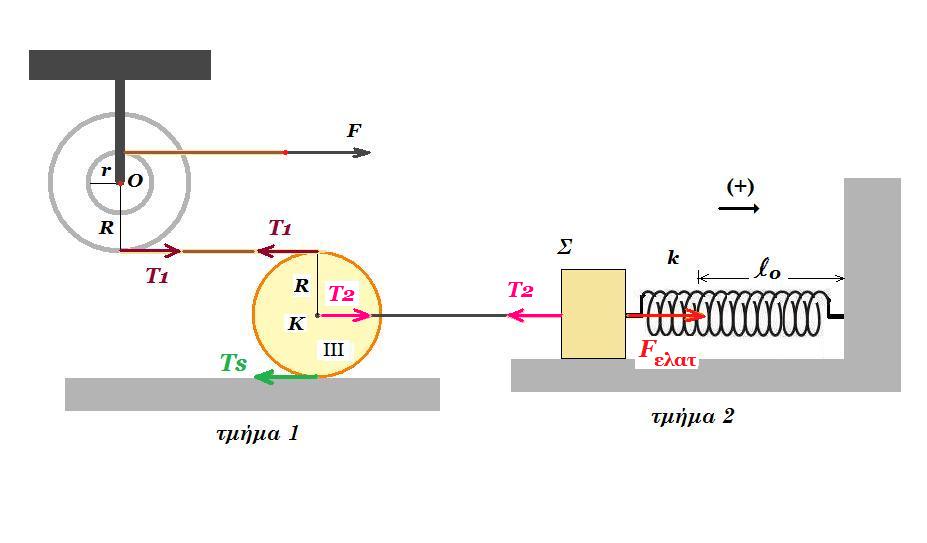
το Σ2 κατέρχεται πάνω στο λείο κεκλιμένο επίπεδο με επιτάχυνση α2 : m2 g ημθ - Τ2 = m2 a2 (1)
το Σ1 ανέρχεται κατακόρυφα με επιτάχυνση α1 : Τ1 - m1 g = m1 a1 (2)
η τροχαλία στρέφεται με γωνιακή επιτάχυνση αγων επειδή η μάζα της είναι αμελητέα έχουμε : Στ(Ο) = 0 => Τ2 r - T1 R = 0 => Τ2 r - T1 2r = 0 => T2 = 2T1 (3)
(1) + 2*(2) + (3) => m2 g ημθ - 2 m1 g = m2 a2 + m1 a1 (4)
για τις ταχύτητες έχουμε : v2 = vB = ω r = ω R/2 = vA / 2 = v1 / 2 => v2 = v1 / 2 => v1 = 2 v2 => a1 = 2 a2 (5)
(4) , (5) => m2 g ημθ - 2 m1 g = m2 a2 + m1 a1 => m2 g ημθ - 2 m1 g = m2 a2 + m1 2 a2 => ( m2 ημθ - 2m1 ) g = ( m2 + 2m1 ) a2 => a2 = g ( m2 ημθ - 2m1 ) / ( m2 + 2m1 )
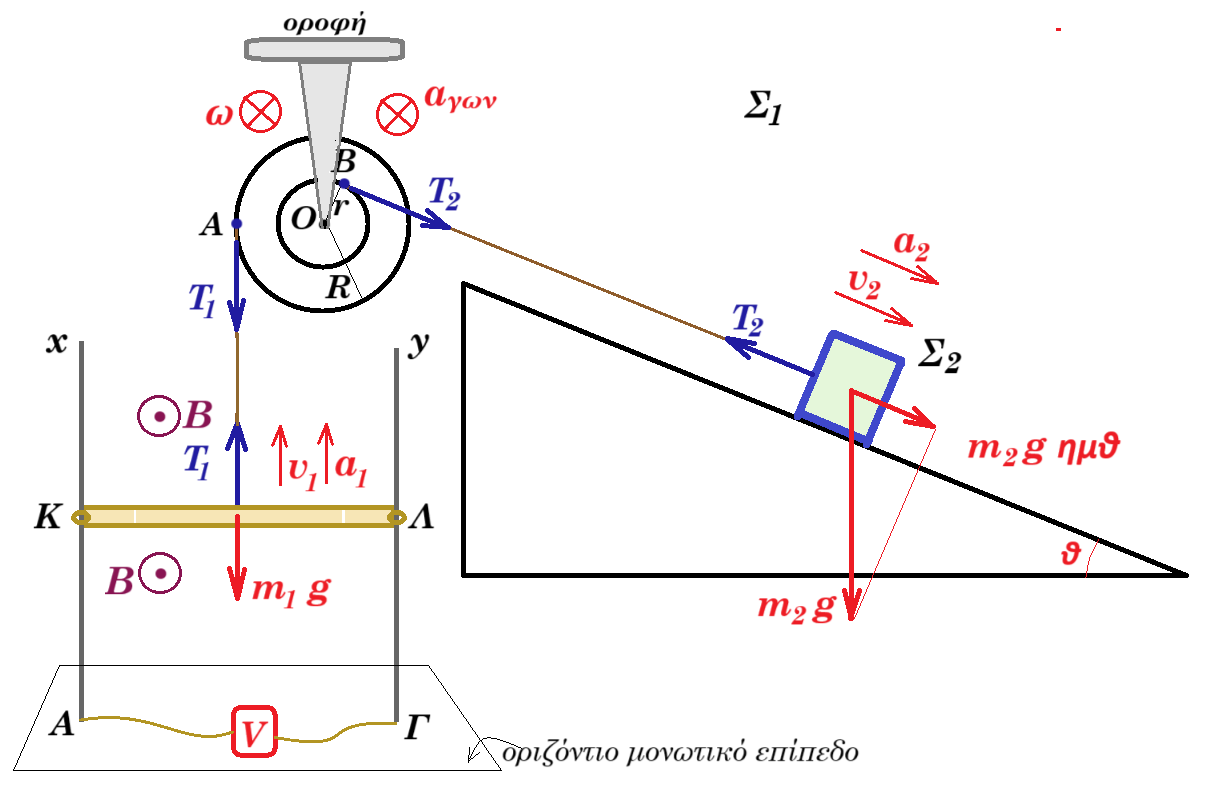
το Σ2 κατέρχεται πάνω στο λείο κεκλιμένο επίπεδο με επιτάχυνση α2 : m2 g ημθ - Τ2 = m2 a2 (1)
η ράβδος ΚΛ ανέρχεται κατακόρυφα με επιτάχυνση α1 : Τ1 - m1 g = m1 a1 (2)
η τροχαλία στρέφεται με γωνιακή επιτάχυνση αγων επειδή η μάζα της είναι αμελητέα έχουμε : Στ(Ο) = 0 => Τ2 r - T1 R = 0 => Τ2 r - T1 2r = 0 => T2 = 2T1 (3)
(1) + 2*(2) + (3) => m2 g ημθ - 2 m1 g = m2 a2 + m1 a1 (4)
για τις ταχύτητες έχουμε : v2 = vB = ω r = ω R/2 = vA / 2 = v1 / 2 => v2 = v1 / 2 => v1 = 2 v2 => a1 = 2 a2 (5)
(4) , (5) => m2 g ημθ - 2 m1 g = m2 a2 + m1 a1 => m2 g ημθ - 2 m1 g = m2 a2 + m1 2 a2 => ( m2 ημθ - 2m1 ) g = ( m2 + 2m1 ) a2 => a2 = g ( m2 ημθ - 2m1 ) / ( m2 + 2m1 )
a1 = 2 g ( m2 ημθ - 2m1 ) / ( m2 + 2m1 )
v1 = a1 t = 2gt ( m2 ημθ - 2m1 ) / ( m2 + 2m1 )
στα άκρα της ράβδου ΚΛ επάγεται τάση Εεπαγ = Β v1 (ΚΛ) η οποία είναι η ένδειξη του ιδανικού βολτομέτρου
αΖ = 3 m/s2 R = 0,1 m
vO = ω 2R aO = aγων 2R => aO = aγων 2R = 2 m/s2 επιτάχυνση στερεού
vB = ω 3R aB = aγων 3R => 3 = aγων 3R => aγων R = 1 m/s2
θ = 0,5 aγων t2 l = R θ = R 0,5 aγων t2 => 6 m = 0,5 1 m/s2 t2 => 12 s2 = t2
xO = 0,5 aO t2 = 0,5 2 m/s2 12 s2 = 12 m
ω = αγων t = 1/0,1 rad/s2 √12 = 10 2√3 = 20√3 rad/s γωνιακή ταχύτητα
vE = ω 4R = 20√3 rad/s 4 0,1 m = 8√3 m/s
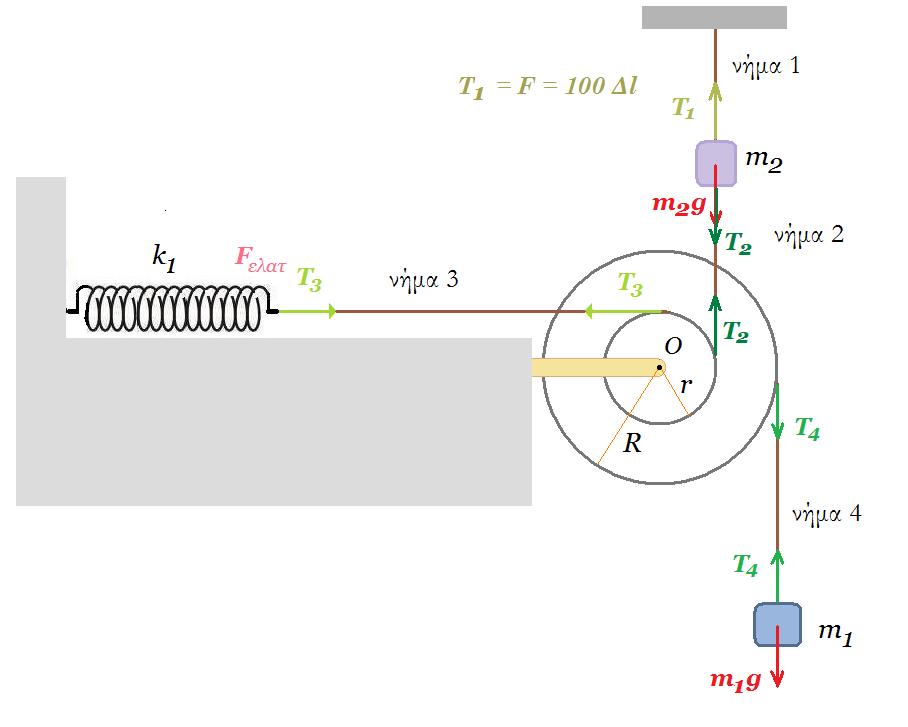
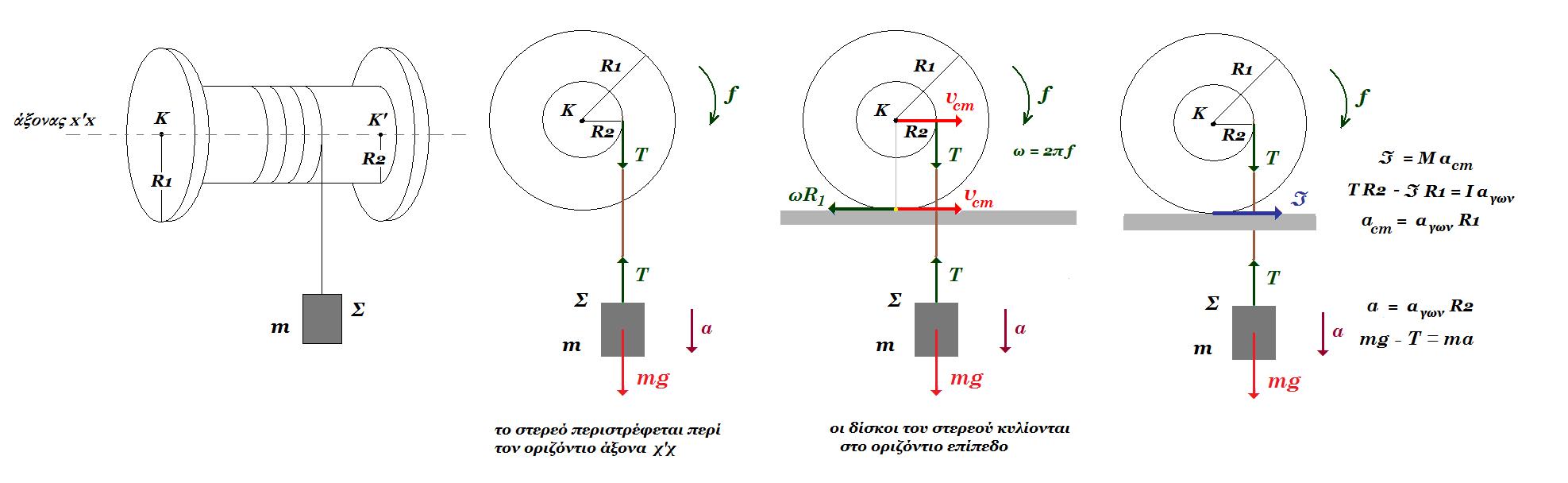
Ομογενής τροχαλία μάζας Μ και αμελητέου πάχους αποτελείται από δύο συγκολλημένους δίσκους με ακτίνες r και R, όπου R =2r. Ο μικρότερος δίσκος ακτίνας r φέρει ένα αυλάκι στην περιφέρειά του γύρω από το οποίο είναι τυλιγμένο πολλές φορές λεπτό, αβαρές και μη εκτατό νήμα, στο ελεύθερο άκρο του οποίου είναι δεμένο βαρύδι μάζας m. Η τροχαλία ακουμπά στην επιφάνεια κεκλιμένου επιπέδου γωνίας κλίσης θ, όπου ημθ=1/10.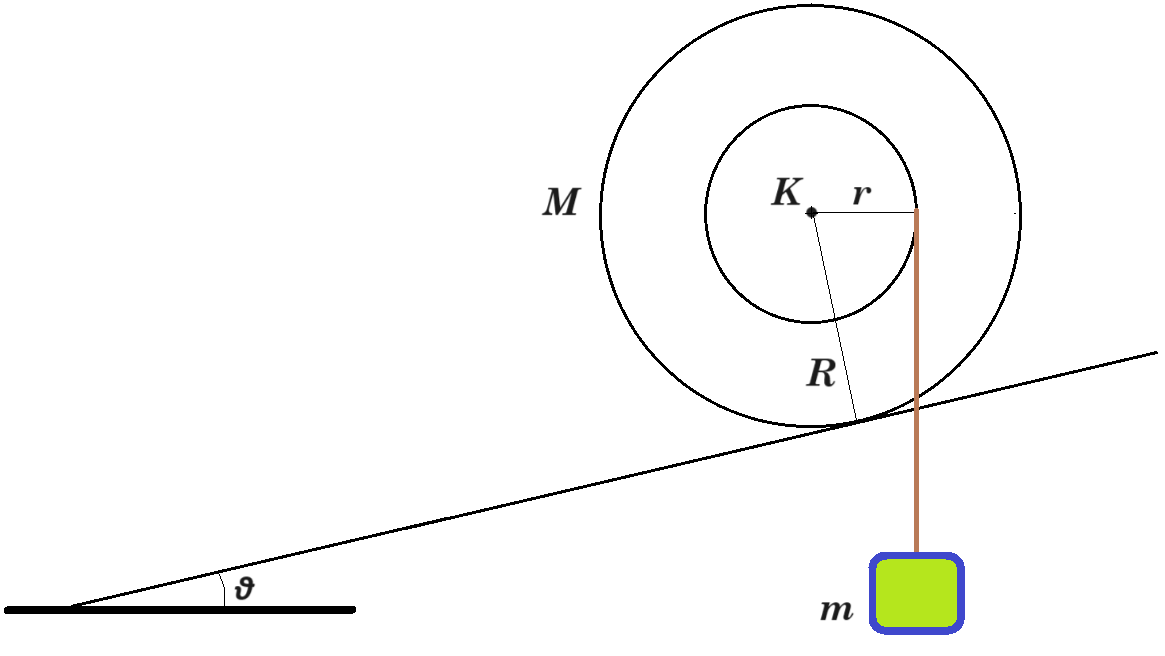 Αν όλη η διάταξη ισορροπεί στατικά και οριακά μέσα σε βαρυτικό πεδίο έντασης μέτρου g, στο οποίο η αντίσταση του αέρα είναι αμελητέα, τότε
Αν όλη η διάταξη ισορροπεί στατικά και οριακά μέσα σε βαρυτικό πεδίο έντασης μέτρου g, στο οποίο η αντίσταση του αέρα είναι αμελητέα, τότε
1) ο συντελεστής της μέγιστης στατικής (οριακής) τριβής μσ μεταξύ τροχαλίας και επιπέδου είναι ίσος με:
i) σφθ ii) εφθ iii) συνθ
2) ο λόγος των μαζών του βαρυδίου προς της τροχαλίας m/M ισούται με
i) 1/6 ii) 1/4 iii) 1/2
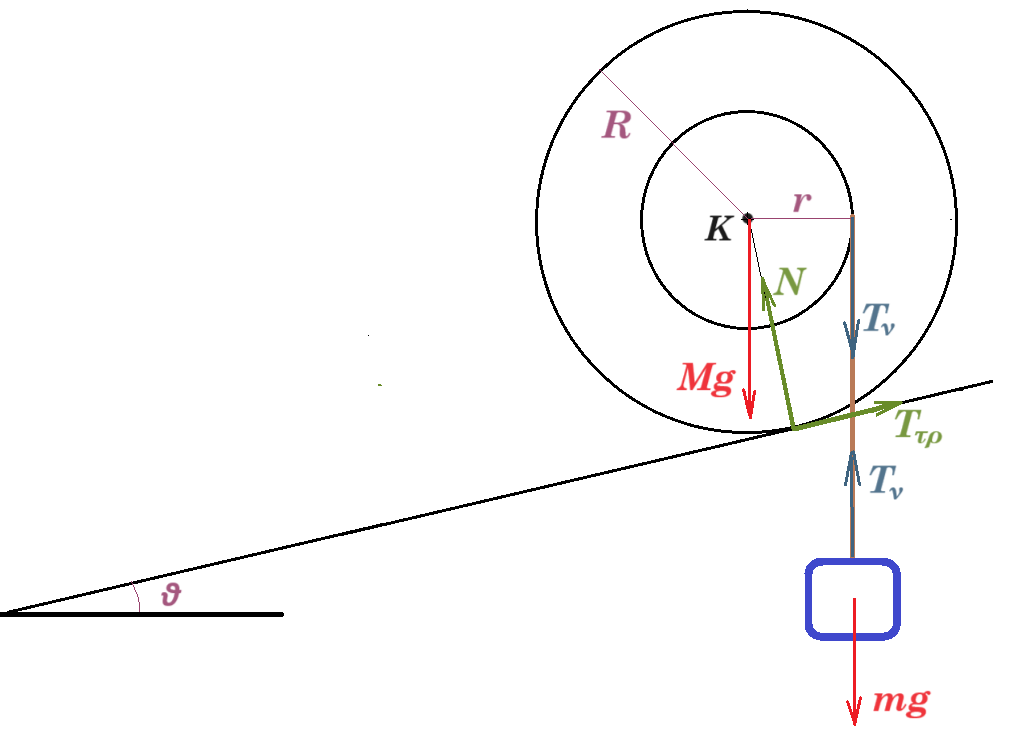 ισορροπία σώματος : mg = Tν
ισορροπία σώματος : mg = Tν
ισορροπία τροχού : Στ(Κ) = 0 => Ττρ R = Τν r => Ττρ R = Τν R/2 => Ττρ = Τν / 2 = mg / 2
ΣFx = 0 => Ττρ - Mg ημθ - Τν ημθ = 0 => mg / 2 - Mg 1/10 - mg 1/10 = 0 => M = 4m
ΣFy = 0 => N - Mg συνθ - Τν συνθ = 0 => N - 4mg συνθ - mg συνθ = 0 => N = 5mg συνθ
μσ = Ττρ / Ν = 1/2 mg / 5 mg συνθ = 1 / 10συνθ = 1/10 / συνθ = ημθ / συνθ => μσ = εφθ
Η δοκός του σχήματος, μήκους l=4m, περιστρέφεται γύρω από κατακόρυφο άξονα ο οποίος διέρχεται από το μέσον της Ο, διαγράφοντας οριζόντιο επίπεδο (το σχήμα σε κάτοψη). Στο ένα άκρο της δοκού έχει προσκολληθεί μια μικρή σφαίρα Σ μάζας 0,1kg, δημιουργώντας έτσι ένα στερεό s. Στο διάγραμμα δίνεται η γωνιακή ταχύτητα του στερεού σε συνάρτηση με το χρόνο, όπου η αρχική γωνιακή ταχύτητα έχει την κατεύθυνση που έχει σημειωθεί, ενώ η θέση της δοκού είναι αυτή του σχήματος με τη σφαίρα στη θέση Α.
t1=0,5s ω = 4 rad/s αγων = 0 v = ω r = ω l/2 L = m v r = m ω (l/2)2 = 0,1kg 4r/s 22m2 = 1,6 kgm2/s dL/dt = Στ(Ο) = m dω/dt (l/2)2 = m αγων (l/2)2 = 0
t2=2s θ = εμβαδόν τραπεζίου = (1s + 2s) 4r/s / 2 = 6 rad αγων = Δω/Δt = (0 - 4r/s) / (2s - 1s) = - 4 r/s2
a = αγων l/2 = - 4 r/s2 2 m = - 8 m/s2 F = m a = 0,1 kg (- 8 m/s2) = - 0,8 N
dL/dt = Στ(Ο) = m dω/dt (l/2)2 = m αγων (l/2)2 = 0,1 kg (- 4 r/s2) 22m2 = - 1,6 kgm2/s
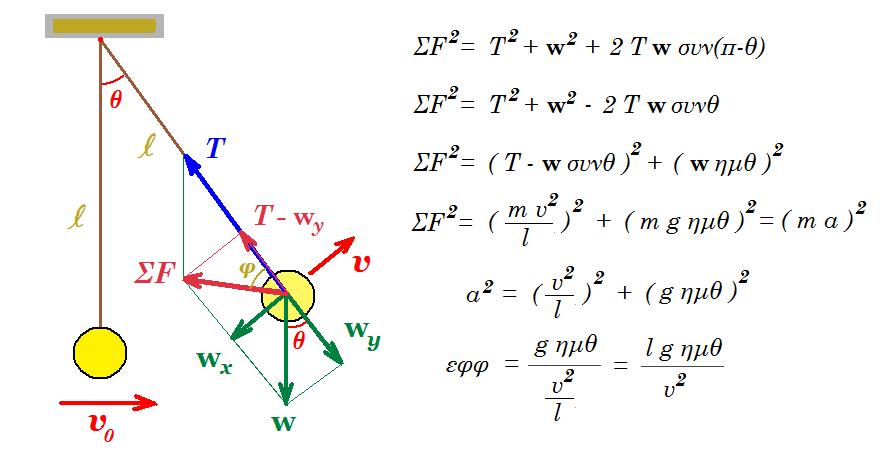
Το σώμα μάζας m=1Kg συνδέεται με το κάτω άκρο αβαρούς, μη ελαστικού νήματος μήκους l = 1,6m. To πάνω άκρο του νήματος συνδέεται σε σταθερό σημείο Α. Το σώμα είναι ακίνητο με το νήμα στην κατακόρυφη διεύθυνση. Δίνουμε στο σώμα οριζόντια ταχύτητα μέτρου υ0 =4√2 m/s προς τα δεξιά. Όταν το νήμα σχηματίζει γωνία θ=600 με την κατακόρυφη διεύθυνση να βρεθούν:
α) Η γραμμική ταχύτητα του σώματος.
β) Η γωνιακή ταχύτητα του σώματος.
γ) Η κεντρομόλος δύναμη που ασκείται στο σώμα.
δ) Η τάση του νήματος
ε) Η δύναμη που ασκείται στο σώμα στη διεύθυνση της εφαπτομένης ( επιτρόχιος δύναμη )
ζ) Η κεντρομόλος επιτάχυνση του σώματος.
η) Ο ρυθμός μεταβολής του μέτρου της γραμμικής ταχύτητας του σώματος ( επιτρόχιος επιτάχυνση )
θ) Η γωνιακή επιτάχυνση του σώματος
h = l - l συν60° = 1,6 - 1,6 ½ = 0,8 m
διατήρηση ενέργειας : ½ m v02 = m g h + ½ m v2 => v02 = 2gh + v2 =>
=> 32 = 2 10 0,8 + v2 => v2 = 32 - 16 = 16 => v = 4 m/s
ω = v / l = 4 m/s / 1,6 m => ω = 2,5 rad/s
FK = m v2 / l = 1 kg (4 m/s)2 / 1,6 m => FK = 10 N
T - mg συν60° = FK => T - 10 Ν ½ = 10 Ν => Τ = 15 Ν
mg ημ60° = 10 Ν √3/2 = 5√3 Ν
ακ = v2 / l = 10 rad/s2
mg ημ60° = m αε => g ημ60° = αε => αε = 10 √3/2 => αε = 5√3 m/s2
αγων = αε / l = 5√3 / 1,6 => αγων = 25√3/8 rad/s2
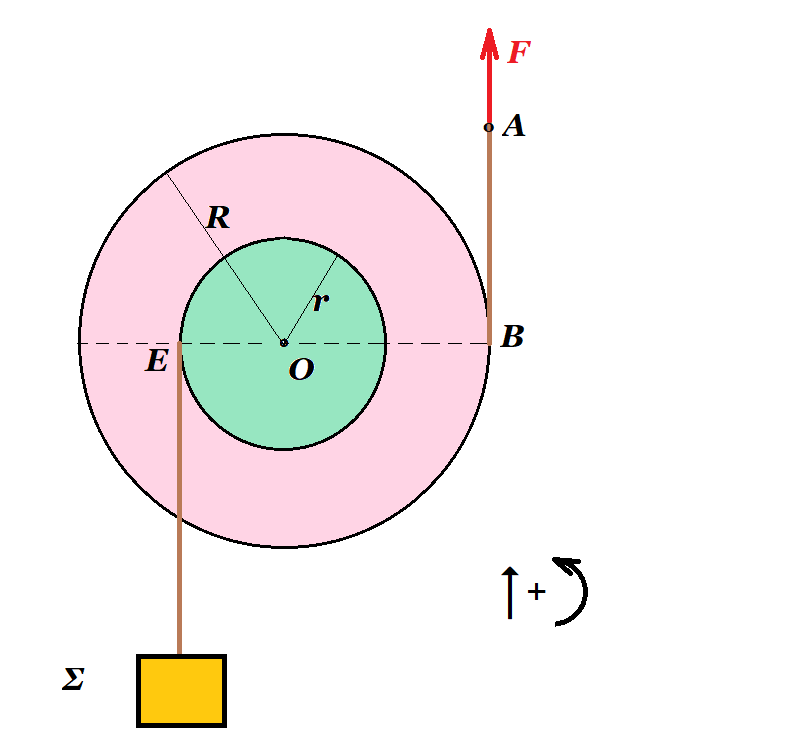
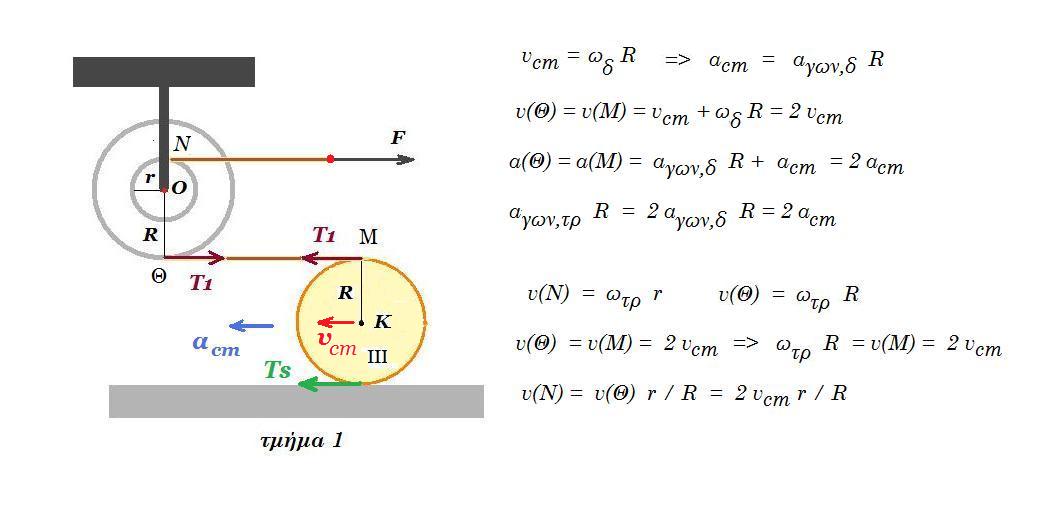
Η διπλή ομογενής τροχαλία του σχήματος, ακτίνας R=0,4m, κινείται κατακόρυφα με την επίδραση μιας κατάλληλης κατακόρυφης δύναμης F, η οποία ασκείται στο άκρο A νήματος, το οποίο έχουμε τυλίξει στο αυλάκι της. Η τροχαλία φέρει ομόκεντρη κυκλική προεξοχή ακτίνας r = 0,2m στην οποία έχουμε τυλίξει ένα δεύτερο νήμα, στο κάτω άκρο του οποίου έχουμε δέσει ένα σώμα Σ. Σε μια στιγμή t1, το άκρο Α του νήματος, στο οποίο ασκείται η δύναμη F, έχει ταχύτητα μέτρου υΑ=1,8m/s, με κατεύθυνση προς τα πάνω, ενώ το σώμα Σ ανεβαίνει επίσης κατακόρυφα, με ταχύτητα μέτρου υΣ=0,6m/s.
i) Να υπολογιστεί η ταχύτητα του κέντρου Ο της τροχαλίας, καθώς και η γωνιακή ταχύτητα περιστροφής της, γύρω από νοητό οριζόντιο άξονα, ο οποίος διέρχεται από το Ο.
Την παραπάνω στιγμή, το σημείο Α έχει κατακόρυφη επιτάχυνση μέτρου αΑ=3,4m/s2, με φορά προς τα πάνω, ενώ το σώμα Σ, κατακόρυφη επιτάχυνση με φορά προς τα κάτω, μέτρου αΣ=0,2m/s2.
ii) Να υπολογιστούν η επιτάχυνση του κέντρου Ο, καθώς και η γωνιακή επιτάχυνση της τροχαλίας.
iii) Να βρεθεί ένα σημείο Γ, της οριζόντιας διαμέτρου της τροχαλίας, το οποίο την στιγμή t1 έχει μηδενική κατακόρυφη επιτάχυνση. Στη συνέχεια να υπολογιστεί η ταχύτητα και η επιτάχυνση του σημείου Γ.
vA = vB = vO + ω R = 1,8 m/s (1) vΣ = vE = vO - ω r = 0,6 m/s (2)
(1) - (2) => ω ( R + r ) = 1,8 - 0,6 => ω ( 0,4 + 0,2 ) = 1,2 => ω = 1,2 / 0,6 = 2 rad/s
(1) => vO + ω R = 1,8 m/s => vO + 2 0,4 = 1,8 => vO = 1,8 - 0,8 = + 1 m/s
aA = aB = aO + αγων R = 3,4 m/s2 (3) αΣ = αE = αO - αγων r = - 0,2 m/s2 (4)
(3) - (4) => αγων ( R + r ) = 3,4 + 0,2 => αγων = 3,6 / 0,6 = 6 rad/s2
(3) => aO + αγων R = 3,4 => aO + 6 0,4 = 3,4 => αΟ = 3,4 - 2,4 = 1 m/s2
aΓ,y = aO + αγων x = 0 => 1 m/s2 + 6 rad/s2 x = 0 => x = - 1/6 m αριστερά του κέντρου Ο
aΓ2 = ( aO + αγων x )2 + ( ω2 x )2 = ( 1 + 6 (-1/6) )2 + ( 22 1/6 )2 = (2/3)2 = 4/9 => aΓ = 2/3 m/s2
vΓ = vO + ω x = 1 m/s + 2 rad/s ( - 1/6 m ) = 1 - 1/3 = 2/3 m/s
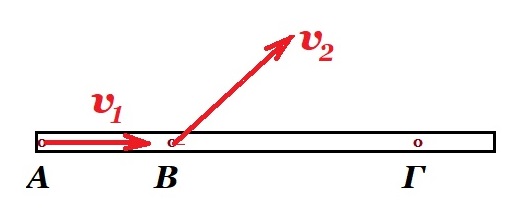
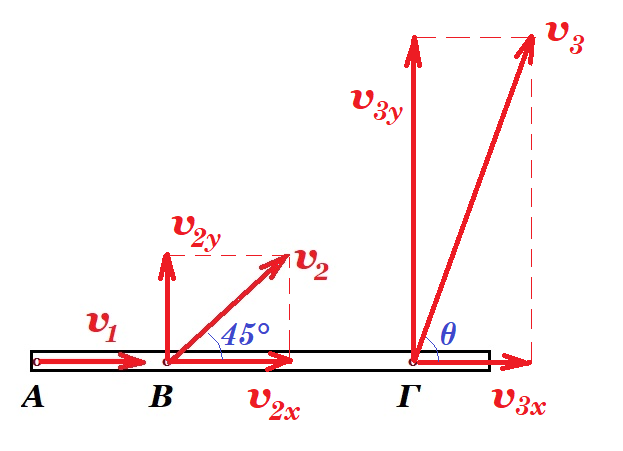
Μια ράβδος κινείται οριζόντια σε λείο οριζόντιο επίπεδο. Κάποια στιγµή το άκρο Α, έχει ταχύτητα µέτρου υ1=1m/s, όπως στο σχήµα. Την ίδια στιγµή το σηµείο Β, το οποίο απέχει από το Α κατά
(ΑΒ)=1m, έχει ταχύτητα υ2 η οποία σχηµατίζει γωνία 45° µε τον άξονα της ράβδου.
Να βρεθεί η ταχύτητα, τη στιγµή αυτή, του σηµείου Γ, αν (ΑΓ)=3m;
η ταχύτητα v2 του σημείου Β της ράβδου σχηματίζει με τον άξονά της γωνία 45° που αναλύεται σε μια συνιστώσα v2x κατά τον άξονα και μια συνιστώσα v2y κάθετη στον άξονα έχουμε v2x = v2y
συμπεραίνουμε ότι η ράβδο και μεταφέρεται και περιστρέφεται
το σημείο Α έχει ταχύτητα v1 κατά τον άξονα της ράβδου εκτελεί μεταφορική κίνηση
η ράβδος περιστρέφεται περί το άκρο της Α με γωνιακή ταχύτητα ω συνεπώς v2y = ω (ΑΒ) και v2x = v1 = 1 m/s άρα v2y = ω (ΑΒ) = v2x = v1 = 1 m/s οπότε v2 = √2 m/s
το σημείο Γ έχει συνιστώσα κατά τον άξονα v3x = v1 = 1 m/s και συνιστώσα κάθετη στον άξονα v3y = ω (ΑΓ) = ω 3 (ΑΒ) = 3 m/s συνεπώς v32 = v3x2 + v3y2 = 12 + 32 = 10 => v3 = √10 m/s εφθ = v3y / v3x = 3
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
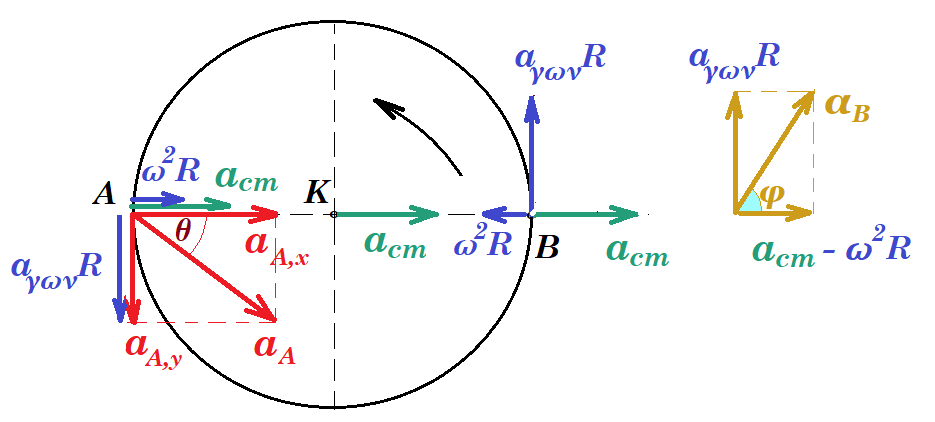
Ένας ομογενής οριζόντιος δίσκος ακτίνας R=1m, κινείται σε λείο οριζόντιο επίπεδο με την επίδραση κατάλληλης δύναμης F. Κάποια στιγμή που ο δίσκος έχει γωνιακή ταχύτητα ω=1rad/s και γωνιακή επιτάχυνση αγων=3rad/s2, διανύσματα κατακόρυφης διεύθυνσης με φορά προς τα πάνω, το σημείο Α στο άκρο μιας ακτίνας στη διεύθυνση x, έχει επιτάχυνση μέτρου αΑ=5m/s2 η οποία σχηματίζει γωνία θ (ημθ=0,6) με την ακτίνα, όπως στο σχήμα. Να υπολογιστούν:
1) η επιτάχυνση του κέντρου μάζας Κ του δίσκου
2) η επιτάχυνση του αντιδιαμετρικού σημείου Β του δίσκου.
η επιτάχυνση του σημείου Α αναλύεται σε μια συνιστώσα κατά το άξονα ΑΚ : aA,x = aA συνθ = 5 m/s2 0,8 = 4 m/s2 και μια συνιστώσα κάθετη στον άξονα ΑΚ : aA,y = aA ημθ = 5 m/s2 0,6 = 3 m/s2
ο δίσκος εκτελεί μεταφορική κίνηση και περιστροφική περί το κέντρο μάζας του Κ
το σημείο Α έχει επιτρόχια επιτάχυνση aA,y = 3 m/s2 κεντρομόλο επιτάχυνση ακ = ω2 R = (1 rad/s)1 1 m = 1 m/s1 και μεταφορική επιτάχυνση acm του κέντρου μάζας Κ του δίσκου η κεντρομόλος ακ και η μεταφορική acm του κέντρου μάζας είναι κατά τον άξονα ΑΚ ομόρροπες συνεπώς ακ + acm = aA,x => 1 m/s2 + acm = 4 m/s2 => acm = 3 m/s2 δηλαδή το κέντρο μάζας Κ του δίσκου έχει επιτάχυνση acm = 3 m/s2
το σημείο Β έχει επιτρόχια επιτάχυνση με μέτρο aΒ,y = 3 m/s2 κεντρομόλο επιτάχυνση ακ = ω2 R = (1 rad/s)1 1 m = 1 m/s1 και μεταφορική επιτάχυνση acm = 4 m/s2 του κέντρου μάζας Κ του δίσκου η κεντρομόλος ακ και η μεταφορική acm του κέντρου μάζας είναι κατά τον άξονα ΑΚ αλλά αντίρροπες συνεπώς aB,x = ακ + acm => - 1 m/s2 + 3 m/s2 => aB,x = 2 m/s2 aB2 = aB,x2 + aB,y2 = 22 + 32 = 13 => aB = √13 m/s2
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Τροχός έχει ακτίνα R και ηρεμεί με το επίπεδό του κατακόρυφο. Την χρονική στιγμή t0=0 ο τροχός αρχίζει να κυλίεται χωρίς να ολισθαίνει, προς τα δεξιά με σταθερή γωνιακή επιτάχυνση αγων. Κάποια χρονική στιγμή t1 η ολική επιτάχυνση του σημείου Α της περιφέρειας του τροχού, το οποίο απέχει από το έδαφος απόσταση ίση με την ακτίνα του τροχού, έχει διεύθυνση κατακόρυφη με φορά προς τα κάτω. Την στιγμή αυτή ο λόγος των μέτρων των ολικών επιταχύνσεων των σημείων Β, που είναι αντιδιαμετρικό του Α και του υψηλότερου σημείου Δ του τροχού έχει τιμή:
α) 1 β) √2 γ) 1/2
=
σημείο Γ στιγμιαία ακίνητο : υcm = ω R => αcm = αγων R
επειδή η συνολική επιτάχυνση του σημείου Α είναι κατακόρυφη προς τα κάτω άρα αcm = ακ = v2/R = ω2R
στο σημείο Β : αΒ2 = ( αcm + ακ )2 + ( αγων R )2 = ( αγων R + αγων R )2 + ( αγων R )2 = 5 ( αγων R )2
στο σημείο Δ : αΔ2 = ( αcm + αγων R )2 + ( ακ )2 = ( αγων R + αγων R )2 + ( αγων R )2 = 5 ( αγων R )2
συνεπώς : αΒ / αΔ = 1
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
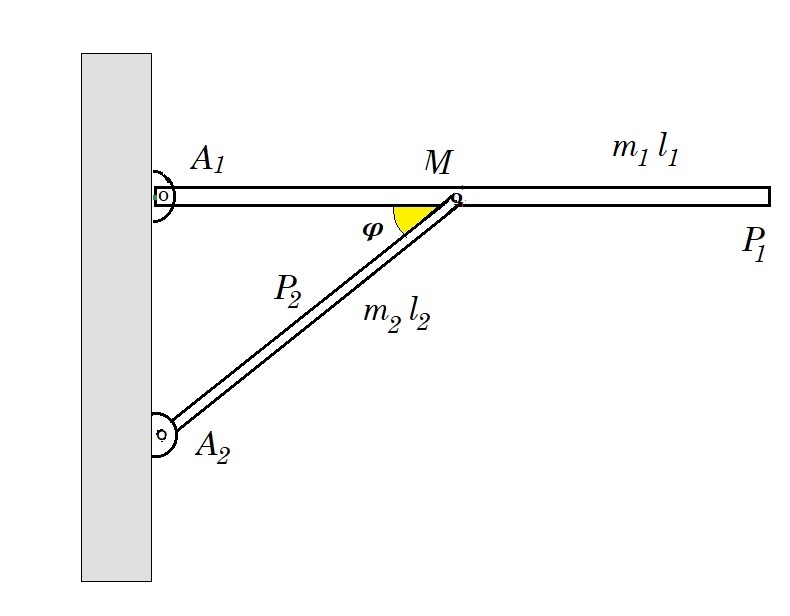
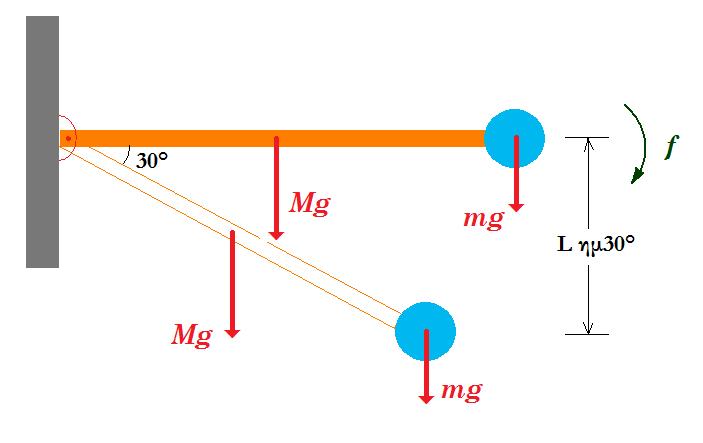
Η λεπτή ομογενής ράβδος Ρ1 μάζας m1=m και μήκους l1, ισορροπεί ακίνητη σε οριζόντια διεύθυνση, με τη βοήθεια μιας δεύτερης λεπτής και ομογενούς ράβδου Ρ2, από άλλο υλικό, μάζας m2=m και μήκους l2, με l1 = 1,6 l2 όπως φαίνεται στο παραπάνω σχήμα. Τα άκρα Α1 και Α2 των ράβδων είναι στερεωμένα σε αρθρώσεις στον ίδιο κατακόρυφο τοίχο ως προς τις οποίες μπορούν να περιστρέφονται χωρίς τριβές. Επιπλέον το άλλο άκρο της ράβδου Ρ2 είναι χαλαρά καρφωμένο στο μέσον Μ της ράβδου Ρ1 εξασφαλίζοντας με αυτόν τον τρόπο την ισορροπία του συστήματος. Στο σημείο σύνδεσης Μ των δύο ράβδων δεν αναπτύσσονται τριβές ενώ αν δεν είναι αρθρωμένες στον κατακόρυφο τοίχο επιτρέπεται η μεταξύ τους σχετική περιστροφή.
Να υπολογίσετε το πηλίκο των μέτρων των δυνάμεων FA2 / FA1 , όπου FA1 και FA2 , οι δυνάμεις που δέχονται αντίστοιχα οι ράβδοι από τις αρθρώσεις.
 l1 = 1,6 l2 άρα συνφ = l1/2 / l2 = 0,8 συνεπώς ημφ = 0,6
l1 = 1,6 l2 άρα συνφ = l1/2 / l2 = 0,8 συνεπώς ημφ = 0,6
ισορροπία ράβδου 1 : ροπές ως προς Α1 : Στ(Α1) = 0 => Ny (A1M) - m1 g (A1M) = 0 => Ny = m1 g = m g (1)
ΣFx = 0 => Nx - FA1 = 0 => Nx = FA1 (2)
ισορροπία ράβδου 2 : ροπές ως προς Α2 : Στ(Α2) = 0 => Nx l2 ημφ - Ny l2 συνφ - m2 g l2/2 συνφ = 0 =>
=> Nx 0,6 - Ny 0,8 - m2 g 1/2 0,8 = 0 =>(1) Nx 0,6 - mg 0,8 - m g 1/2 0,8 = 0 => Nx 0,6 = mg 1,2 =>
=> Nx = 2 mg (3)
ΣFx = 0 => FA2,x - Nx = 0 =>(3) FA2,x = Nx = 2 mg
ΣFy = 0 => FA2,y - Ny - m2 g = 0 =>(1) FA2,y = mg + mg = 2mg
FA22 = FA2,x2 + FA2,y 2 = 4 m2g2 + 4m2g2 => FA2 = 2√2 mg
(2) , (3) => FA1 = Nx = 2 mg FA1 / FA2 = 1/√2
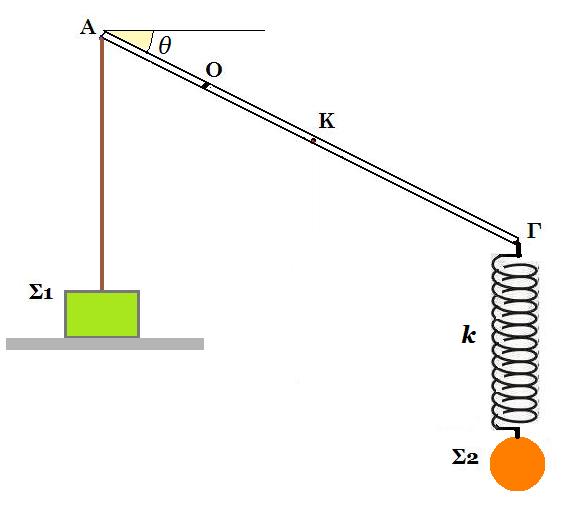 Λεπτή ομογενής ράβδος (ΑΓ) μάζας Μ = 3 kg και μήκους L μπορεί να περιστρέφεται χωρίς τριβές γύρω από οριζόντιο άξονα που διέρχεται από σημείο Ο για το οποίο ισχύει (ΑΟ) = L/4. Στο άκρο της Α είναι δεμένο αβαρές και μη εκτατό νήμα το άλλο άκρο του οποίου είναι ακλόνητα στερεωμένο σε σώμα Σ1 μάζας m1 που ισορροπεί πάνω σε λείο οριζόντιο δάπεδο. Στο άλλο άκρο της ράβδου είναι συνδεδεμένο το πάνω άκρο ιδανικού κατακόρυφου ελατηρίου σταθεράς k = 100N/m που στο κάτω μέρος του ισορροπεί σώμα Σ2 μάζας m2 = 1 kg. Δίνεται g = 10 m/s2.
Λεπτή ομογενής ράβδος (ΑΓ) μάζας Μ = 3 kg και μήκους L μπορεί να περιστρέφεται χωρίς τριβές γύρω από οριζόντιο άξονα που διέρχεται από σημείο Ο για το οποίο ισχύει (ΑΟ) = L/4. Στο άκρο της Α είναι δεμένο αβαρές και μη εκτατό νήμα το άλλο άκρο του οποίου είναι ακλόνητα στερεωμένο σε σώμα Σ1 μάζας m1 που ισορροπεί πάνω σε λείο οριζόντιο δάπεδο. Στο άλλο άκρο της ράβδου είναι συνδεδεμένο το πάνω άκρο ιδανικού κατακόρυφου ελατηρίου σταθεράς k = 100N/m που στο κάτω μέρος του ισορροπεί σώμα Σ2 μάζας m2 = 1 kg. Δίνεται g = 10 m/s2.
1) Να υπολογίσετε την ελάχιστη τιμή της μάζας m1 ώστε το σύστημα των σωμάτων να ισορροπεί.
Στη συνέχεια αντικαθιστούμε το σώμα Σ1 με σώμα Σ3 μάζας m3 = 1,5m1. Προκαλούμε στο ελατήριο επιπλέον επιμήκυνση d και την χρονική στιγμή t0 = 0 το αφήνουμε ελεύθερο.
Να υπολογίσετε :
2) τη μέγιστη τιμή του d ώστε η ράβδος να ισορροπεί σε όλη τη διάρκεια της ταλάντωσης του Σ2.
3) τη συνάρτηση του μέτρου της δύναμης που δέχεται το Σ3 από το οριζόντιο επίπεδο με την απομάκρυνση της ταλάντωσης του Σ2 θεωρώντας ότι d = dmax από το προηγούμενο ερώτημα και τη θετική φορά προς τα κάτω.
4) το μέγιστο μέτρο της δύναμης που ασκεί ο άξονας στη ράβδο στη διάρκεια της ταλάντωσης του Σ2.
Απαντήσεις : 1) m1 = 6 kg, 2) d = 0,1 m, 3) Ν = 30 - 300x S.I.
4) F = 140 N
θετική κατεύθυνση : κατακόρυφη προς τα κάτω
ισορροπία Σ2 : m2 g = Fελατ = k x0 => Fελατ = 10 N & x0 = 10/100 = 0,1 m |F'ελατ| = |Fελατ| = 10 N
ισορροπία ράβδου :
ροπές ως προς Ο : Στ(Ο) = 0 => Τ l/4 συνθ - Mg l/4 συνθ - F'ελατ 3l/4 συνθ = 0 => Τ = Mg + 3F'ελατ = 30 + 30 => T = 60 N
ισορροπία Σ1 : m1 g = T + N => m1 10 = 60 + 0 => m1 = 6 kg η ελάχιστη μάζα όταν η αντίδραση από το δάπεδο είναι μηδέν Ν = 0
Α Α Τ σώματος Σ2 k = m2 ω2 => ω2 = k / m2 = 100/1 => ω = 10 rad/s
x(t) = d ημ(10t + π/2) v(t) = d 10 συν(10t + π/2) α(t) = - d 100 ημ(10t + π/2)
ΣF = m2 a => Fελατ + m2 g = m2 α => Fελατ = - 1 10 - 1 d 100 ημ(10t + π/2) => Fελατ = - 10 - d 100 ημ(10t + π/2) F'ελατ = 10 + d 100 ημ(10t + π/2)
ισορροπία Σ3 : m3 g = T + N => T = m3 g - N = 90 - N m3 = 1,5m1 = 1,5 . 6 kg = 9 kg
ισορροπία ράβδου :
ροπές ως προς Ο : Στ(Ο) = 0 => Τ l/4 συνθ - Mg l/4 συνθ - F'ελατ 3l/4 συνθ = 0 =>
=> 90 - N = 30 + 3 [ 10 + d 100 ημ(10t + π/2) ] => 90 - N = 30 + 30 + 3d 100 ημ(10t + π/2) =>
=> N = 30 - 3d 100 ημ(10t + π/2) => N = 30 - d 300 ημ(10t + π/2) ή Ν = 30 - 300 x
ημ(10t + π/2) = 1 => N = 30 - 3d όταν N = 0 τότε d = 0,1 m μέγιστη τιμή για να μην χαθεί η επαφή του Σ3 με το δάπεδο
ημ(10t + π/2) = -1 => N = 30 + d 300 > 0
ΣFy = 0 => F(O) - T - Mg - F'ελατ = 0 => F(O) = 90 - N + Mg + F'ελατ =>
=> F(O) = 90 - [ 30 - d 300 ημ(10t + π/2) ] + 30 + [ 10 + d 100 ημ(10t + π/2) ] =
=> F(O) = 100 + d 400 ημ(10t + π/2)
ημ(10t + π/2) = 1 d = 0,1 m F(O) = 100 + 0,1 400 = 140 N μέγιστη δύναμη που δέχεται η ράβδος στο στήριγμα Ο 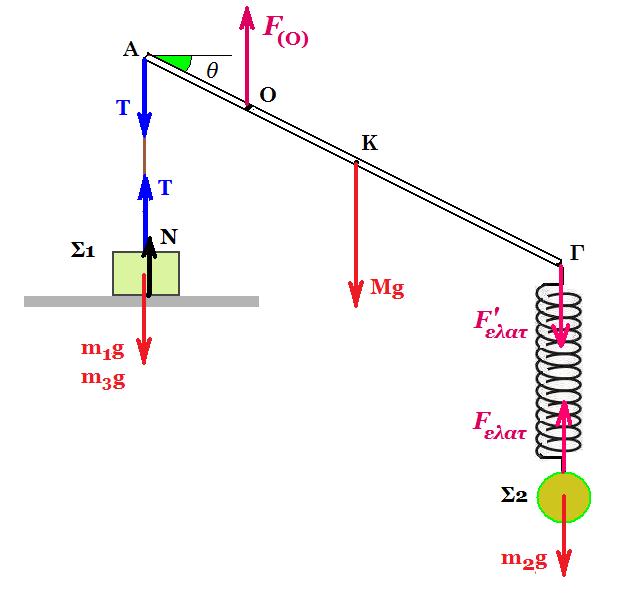
μηχανική στερεού σώματος

Αβαρής ράβδος μήκους 3d (d=1m) μπορεί να στρέφεται σε κατακόρυφο επίπεδο γύρω από οριζόντιο άξονα, που είναι κάθετος σε αυτήν και διέρχεται από το Ο. Στο άκρο Α που βρίσκεται σε απόσταση 2d από το Ο υπάρχει σημειακή μάζα mΑ και στο σημείο Γ, που βρίσκεται σε απόσταση d από το Ο υπάρχει επίσης σημειακή μάζα mΓ = 6 kg. Στο άλλο άκρο της ράβδου, στο σημείο Β, είναι αναρτημένη μέσω αβαρούς μη εκτατού νήματος, τροχαλία μάζας Μ = 4 kg από την οποία κρέμονται οι μάζες m1 και m2 = m3 =1 kg. Η τροχαλία μπορεί να περιστρέφεται γύρω από οριζόντιο άξονα Ο΄. Το σύστημα ισορροπεί με όλα τα μέλη του ακίνητα και τη ράβδο στην οριζόντια θέση.
A1. Να σχεδιάσετε τις δυνάμεις που ασκούνται στις μάζες m1 , m2 , m3 καθώς και στην τροχαλία. Να υπολογίσετε την τιμή της μάζας m1.
Α2. Να υπολογίσετε την τιμή της μάζας mΑ
Κάποια στιγμή κόβουμε το νήμα που συνδέει τις μάζες m2 , m3. Η ράβδος συνεχίζει να ισορροπεί σε οριζόντια θέση υπό την επίδραση κατάλληλης ροπής ζεύγους δυνάμεων. Η m1 κατέρχεται με σταθερή επιτάχυνση μέτρου a1=2m/s2 ενώ η μάζα m2 ανέρχεται. Το νήμα δεν ολισθαίνει στο αυλάκι της τροχαλίας.
Α3. Να υπολογίσετε τη ροπή του ζεύγους δυνάμεων που ασκείται στη ράβδο, ώστε αυτή να ισορροπεί σε οριζόντια θέση.
Μετά από λίγο κόβουμε το νήμα Ο΄Β, που συνδέει την τροχαλία με τη ράβδο. Η ράβδος αρχίζει να περιστρέφεται σε κατακόρυφο επίπεδο, γύρω από τον οριζόντιο άξονα που διέρχεται από το Ο.
Με δεδομένο ότι δεν εμφανίζεται τριβή στον άξονα κατά την περιστροφή της ράβδου, η μηχανική ενέργεια του συστήματος των μαζών mΑ και mΓ διατηρείται σταθερή.
Α4. Να υπολογίσετε τη γωνιακή ταχύτητα της ράβδου τη στιγμή που διέρχεται από την κατακόρυφη θέση καθώς και την επιτάχυνση της μάζας mΓ την ίδια στιγμή.
Όταν η σημειακή μάζα mΑ φτάνει στο κατώτατο σημείο, δηλαδή τη στιγμή που η ράβδος είναι κατακόρυφη, συγκρούεται πλαστικά με ακίνητη σημειακή μάζα m4 = 5kg.
Α5. Να υπολογίσετε τη γραμμική ταχύτητα της σημειακής μάζα mΑ αμέσως μετά την κρούση καθώς και την απώλεια μηχανικής ενέργειας κατά την κρούση.
Α6. Να υπολογίσετε το συνφ της γωνίας φ που σχηματίζει η ράβδος με την κατακόρυφη τη στιγμή που μηδενίζεται η γωνιακή της ταχύτητα.
Δίνεται: g=10 m/s2.
Α1. ισορροπία Σ3 : m3 g = T2,3 = 10 N ισορροπία Σ2 : m2 g + T2,3 = T2,τρ = 10 + 10 = 20 N
ισορροπία Σ1 : m1 g = T1,τρ
ισορροπία τροχαλίας : Στ(Ο') = 0 => T1,τρ R = T2,τρ R => T1,τρ = T2,τρ = 20 N => m1 = 2 kg
ΣFy = 0 => Tτρ,ραβ = Μτρ g + 2 T1,τρ = 40 + 2 20 => Tτρ,ραβ = 80 N
ισορροπία ράβδου : Στ(Ο) = 0 => mΑ g (ΟΑ) + mΓ g (ΟΓ) = Tτρ,ραβ (ΟΒ) => mΑ g 2m + 60N 1m = 80N 1m => mA = 1 kg
Α3. m1 g - T1,τρ = m1 a1 => 20 - T1,τρ = 4 => T1,τρ = 16 N
a1 = R αγων Στ(Ο') = T1,τρ R - T2,τρ R = ½ M R2 αγων => T1,τρ - T2,τρ = ½ M α1 =>
=> 16 - T2,τρ = ½ 4 2 => T2,τρ = 12 Ν
T2,τρ - m2 g = m2 a2 => 12 - 10 = 1 a2 => a2 = 2 m/s2 το σώμα (2) ανέρχεται με επιτάχυνση a2 = 2 m/s2
ΣFy = 0 => Tτρ,ραβ = Μτρ g + T1,τρ + T2,τρ = 40 + 16 + 12 => Tτρ,ραβ = 68 N
ισορροπία ράβδου : Στ(Ο) = mΑ g (ΟΑ) + mΓ g (ΟΓ) - Tτρ,ραβ (ΟΒ) = 10 2 + 60 1 - 68 1 = 12 Nm αριστερόστροφη ροπή
για να ισορροπεί οριζόντια η ράβδος πρέπει να ασκηθεί δεξιόστροφη ροπή με μέτρο 12 Nm
Α4. mA g 2d + mΓ g d = ½ mA vA2 + ½ mΓ vΓ2 =>
=> mA g 2d + mΓ g d = ½ mA ω2 4d2 + ½ mΓ ω2 d2 =>
=> 10 2 + 60 = ½ 1 ω2 4 + ½ 6 ω2 =>
=> 20 + 60 = 2 ω2 + 3 ω2 => ω2 = 80 / 5 = 16 => ω = 4 rad/s
η μάζα mΓ έχει κεντρομόλο επιτάχυνση ακ(Γ) = υΓ2 / d = ω2 d = 16 1 = 16 m/s2
Α5. διατήρηση στροφορμής : mA vA 2d + mΓ v d = mA ω 4d2 + mΓ ω d2 = ( mA + m4 ) ω' 4d2 + mΓ ω' d2 =>
=> 1 4 4 + 6 4 1 = ( 1 + 5 ) ω' 4 + 6 ω' 1 => 16 + 24 = 30 ω' => ω' = 4/3 rad/s
ΔK = Κτελ - Καρχ = ½ ( mA + m4 ) ω'2 4d2 + ½ mΓ ω'2 d2 - ( ½ mA ω2 4d2 + ½ mΓ ω2 d2 ) = ½ 6 16/9 4 + ½ 6 16/9 - ( ½ 1 16 4 + ½ 6 16 ) = 240/9 - 80 = - 480/9 Joule = - 160/3 Joule
Α6. διατήρηση ενέργειας : ½ ( mA + m4 ) ω'2 4d2 + ½ mΓ ω'2 d2 = ( mA + m4 ) g 2d (1 - συνφ) + mΓ g d (1 - συνφ) =>
=> ½ 6 16/9 4 + ½ 6 16/9 = 60 2 (1 - συνφ) + 60 1 (1 - συνφ) =>
=> 64/3 + 16/3 = 120 (1 - συνφ) + 60 (1 - συνφ) =>
=> 80/3 = 180 - 180 συνφ => 180 συνφ = 180 - 80/3 = 460/3 => συνφ = 460/540 = 46/54 = 23/27
01. Το στερεό του σχήματος αποτελείται από δίσκο (Ι) μάζας Μ και ακτίνας R και από μικρότερο δίσκο (ΙΙ) μάζας m και ακτίνας r , καρφωμένο στο σημείο Ο της περιφέρειας του δίσκου (Ι). Το σύστημα είναι σε κατακόρυφη θέση σε ισορροπία, μπορεί να περιστρέφεται χωρίς τριβές γύρω από οριζόντιο άξονα που διέρχεται από σημείο Α της περιφέρειας του δίσκου (Ι). Στρέφουμε το σύστημα των δίσκων περί το σημείο Α κατά πολύ μικρή γωνία θ (θ < 5°) και αφήνουμε το σύστημα ελεύθερο να κινηθεί. Δείξτε ότι θα εκτελέσει Α.Α.Τ. και βρείτε την συχνότητα ταλάντωσης.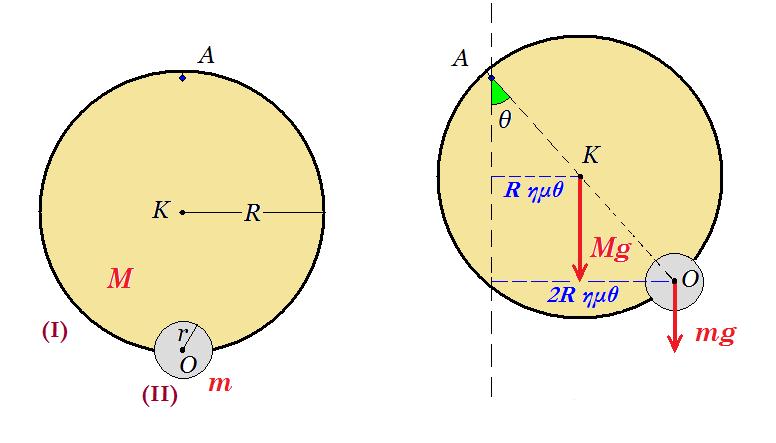
ροπές ως προς Α : Στ(Α) = Ι(Α) αγων =>
=> - Mg Rημθ - mg 2Rημθ = { ½ M R2 + M R2 + ½ m r2 + m (2R)2 } αγων =>
=> - (M + 2m) g Rημθ = { 3/2 M R2 + ½ m r2 + m 4R2 } αγων =>
=> - (M + 2m) g Rημθ = { 3MR2 + 8mR2 + m r2 } αγων => ημθ » θ πολύ μικρή γωνία θ < 5°
Στ(Α) = - (M + 2m) g R θ = { 3MR2 + 8mR2 + m r2 } αγων =>
=> - (M + 2m)gR / { 3MR2 + 8mR2 + m r2 } θ = αγων => - ω2 θ = αγων
το στερεό θα εκτελέσει Α.Α.Τ. με σταθερά : D = (M + 2m)gR διότι Στ(Α) = - (M + 2m) g R θ η συνισταμένη ροπή είναι ανάλογη της γωνίας θ
ω2 = (M + 2m)gR / { 3MR2 + 8mR2 + m r2 } Τ = 2π/ω f = 1/T
- D x = a D = m ω2 [D] = N/m = kg m/s2 / m = kg / s2 = [D]
02. Δίσκος ακτίνας R = 0,2 m κυλίεται χωρίς να ολισθαίνει και η γωνιακή του ταχύτητα μεταβάλλεται με το χρόνο όπως φαίνεται στο διάγραμμα. Το διάστημα που έχει διανύσει ο δίσκος μέχρι την χρονική στιγμή t = 2 s είναι
α) s = 2 m β) s = 4 m γ) s = 50 m 
υ = ω R aγων = Δω / Δt = 10 rad/s / 2 s = 5 rad/s2 θ = ½ αγων t2 = ½ 5 22 = 10 rad s = θ . R = 10 rad . 0,2 m = 2 m
03. Μία οριζόντια ράβδος ΑΒ μήκους L εκτελεί στροφική κίνηση με σταθερή γωνιακή ταχύτητα ίση με ω γύρω από σταθερό κατακόρυφο άξονα περιστροφής που διέρχεται από το άκρο της Α. Το μέσο Μ της ράβδου έχει κεντρομόλο επιτάχυνση ίση με
α) ακ = ω2 L β) ακ = ω2 L/2 γ) ακ = ω2 L/4 δ) ακ = ω L2 /4
ακ2 = υ2 / r = ω2 r = ω2 L/2
04. Ένας τροχός κυλάει σε οριζόντιο έδαφος και η ταχύτητα του ανώτερου σημείου του είναι κάποια στιγμή τριπλάσια απο την ταχύτητα του άξονα περιστροφής του. Η ταχύτητα του κατώτερου σημείου του θα είναι:
α) Ίση με την ταχύτητα του άξονα περιστροφής
β) Αντίθετη της ταχύτητας του άξονα περιστροφής
γ) Διπλάσια της ταχύτητας του άξονα περιστροφής
δ) Η μισή της ταχύτητας του άξονα περιστροφής.
05. Τροχός ακτίνας R κυλίεται χωρίς να ολισθαίνει σε οριζόντιο επίπεδο. Κάποια χρονική στιγμή το κέντρο μάζας του τροχού έχει ταχύτητα μέτρου υcm . Έστω Α το ανώτερο σημείο της περιφέρειας του τροχού και Γ ένα σημείο του τροχού που βρίσκεται στην οριζόντια
διάμετρο και απέχει απόσταση ΓΚ = R/2 από το κέντρο Κ του τροχού, όπως φαίνεται στο σχήμα. Ο λόγος υΓ /υΑ των μέτρων των ταχυτήτων των σημείων Γ και Α είναι ίσος με
α) √3/4 β) √5/4 γ) 1/4
υΚ = υcm υA = υcm + ωR = 2 υcm = 2 ωR
υΓ2 = υcm 2 + (ωR/2) 2 = υcm 2 + (ωR)2 / 4 = υcm 2 + υcm 2 / 4 = 5/4 υcm 2 => υΓ = √5/2 υcm συνεπώς υΓ / υΑ = √5/4 
06. Η τετράγωνη πλάκα ΚΛΜΝ πλευράς α, του σχήματος μπορεί να περιστρέφεται γύρω από ακλόνητο άξονα που διέρχεται από το κέντρο της Ο και είναι κάθετος σε αυτή. Στην πλάκα ασκούνται οι δυνάμεις F1 και F2 με μέτρα F1 = F2 = F. Η δύναμη που πρέπει να ασκηθεί στο στερεό για να ισορροπεί είναι:
α) η δύναμη FΑ , μέτρου F.
β) η δύναμη FΒ , μέτρου 2F.
γ) η δύναμη FΓ , μέτρου 2F.
07. Στη ράβδο του σχήματος που έχει μήκος L, ενεργεί η σταθερού μέτρου δύναμη F. Να γίνει γραφική παράσταση της αλγεβρικής τιμής της ροπής της δύναμης ώς προς το άκρο Α της ράβδου, συναρτήσει της γωνίας φ που σχηματίζει η δύναμη με την ράβδο. 
τ = F . ημφ . 2L/3 = 2.F.L/3 . ημφ
08. Η ράβδος ΑΒ ισορροπεί στηριζόμενη στο υποστήριγμα που διέρχεται από το μέσο της Κ. Σε απόσταση d από το Κ προς τα δεξιά υπάρχει σώμα μάζας m = 2 kg που είναι τοποθετημένο πάνω στη ράβδο. Σε απόσταση 2d προς τα αριστερά από το Κ υπάρχει ελατήριο σταθεράς k = 100 N/m το οποίο συγκρατεί την ράβδο σε οριζόντια θέση. Αν g = 10 m/s2 το ελατήριο
α) είναι στο φυσικό του μήκος
β) έχει συπείρωση Δℓ = 0,2 m
γ) έχει συπείρωση Δℓ = 0,1 m
δ) έχει επιμήκυνση Δℓ = 0,2 m
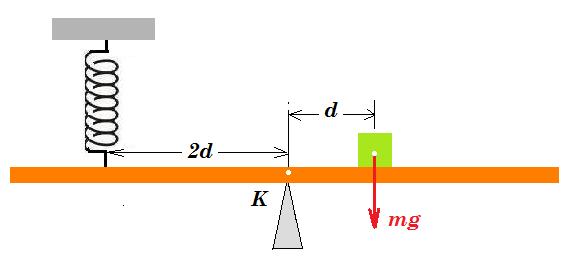
20 d = 2 d 100 x => x = 0,1 m συσπείρωση διότι η δύναμη ελατηρίου είναι κατακόρυφη προς τα κάτω
09. Ο τροχός ακτίνας R του σχήματος διαθέτει μικρό αυλάκι ακτίνας r γύρω απο το οποίο είναι τυλιγμένο λεπτό νήμα. Αν τραβήξουμε το νήμα ώστε ο τροχός να κυλίσει χωρις ολίσθηση τότε όταν το μήκος του οριζόντιου τμήματος του νήματος αυξηθεί κατά L, ο τροχός θα έχει μετατοπισθεί κατά :
α) L β) RL/r γ) rL/R δ) (R+r)L/r
το άκρο Α του νήματος θα έχει μετατοπιστεί κατά :
α) L β) RL/r γ) rL/R δ) (R+r)L/r
L = r θ θ = ω Δτ xΚ = υΚ Δt = ω R Δt = θ R = R L / r
υΑ = υΚ + ωr = ω R + ω r xA = υA Δt = ( ω R + ω r ) Δt = θ ( R + r ) = L ( R + r ) /r
vK = ω R => αK = αγων R L = r θ θ = ½ αγων t2 ω = αγων t
xK = ½ αK t2 = ½ αγων R t2 = R θ => xK = L R / r
vA = vK + ω r = ω (R + r) = vK (R + r) / R
xA = xK (R + r) / R => xA = L R / r (R + r) / R => xA = L (R + r) / r
10. Η τροχαλία του σχήματος έχει τυλιγμένο στο αυλάκι της αβαρές και μη εκτατό νήμα του οποίου το άλλο άκρο είναι σταθερά δεμένο στην οροφή. Αφήνουμε το δίσκο ελεύθερο και αυτός κατέρχεται με σταθερή επιτάχυνση, ενώ το νήμα ξετυλίγεται χωρίς να γλυστρά στο αυλάκι του. Ο λόγος υΑ /υΓ των μέτρων των
ταχυτήτων των σημείων Α και Γ που βρίσκονται στη κατακόρυφη διάμετρο του δίσκου είναι
α) 1/2 β) 1 γ) 2
11. Ένα στερεό αποτελείται από δύο ομοαξονικούς κυλίνδρους κολλημένους μεταξύ τους που έχουν ακτίνες R και 2R. Το στερεό μπορεί να περιστρέφεται γύρω από τον κοινό οριζόντιο άξονα των δύο κυλίνδρων σαν ένα σώμα. Στην περιφέρεια του κυλίνδρου ακτίνας R έχουμε τυλίξει αβαρές μη εκτατό νήμα. Τραβάμε το νήμα οριζόντια με επιτάχυνση α = 3 m/s2 ώστε το νήμα να ξετυλίγεται και το στερεό να κυλίεται χωρίς να ολισθαίνει. Nα βρείτε:
α) Την επιτάχυνση του κέντρου μάζας του στερεού.
β) Όταν έχει ξετυλιχθεί μήκος νήματος ℓ = 5 m, πόσο έχει μετακινηθεί το κέντρο μάζας του στερεού.
γ) Πόση είναι η γωνιακή ταχύτητα του στερεού εκείνη τη στιγμή (αν δίνεται ότι η ακτίνα του μικρού κυλίνδρου είναι R = 0,1 m).
δ) Να βρεθεί η ταχύτητα του υψηλότερου σημείου του στερεού εκείνη τη στιγμή.
[ α) 2 m/s2 β) 10 m γ) 10√10 rad/s δ) 4√10 m/s ] 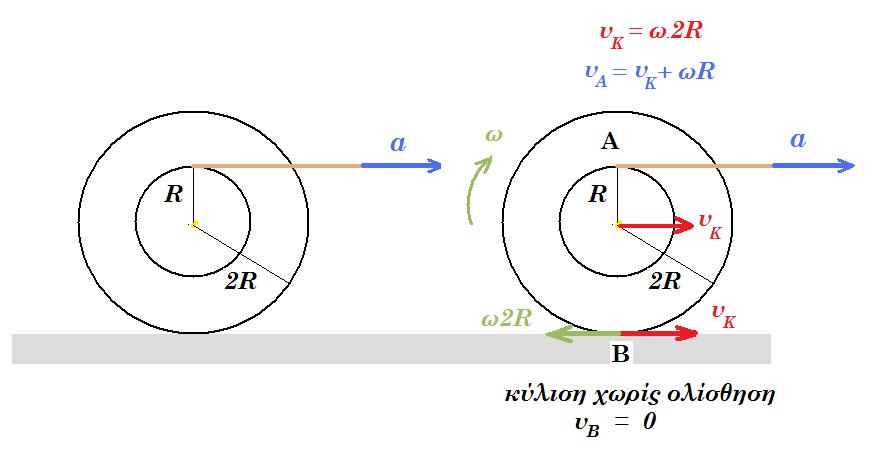
(Α) αΚ = αγων . 2R & α = αΚ + αγων . R => α = αγων . 2R + αγων . R =>
=> 3 m/s2 = 3 R αγων => αγων .R = 1 m/s2 τότε αΚ = 2 m/s2
(Β) l = N 2πR θ = Ν 2π l = ½ . αγων R . t2 &
xK = ½ . αΚ . t2 => xK / l = αΚ / αγων R = 2 => xK / l = 2 => xK = 10 m
(Γ) l = ½ . αγων R . t2 => 5 = ½ . 1 . t2 => t = √10 s
ω = αγων . t = αΚ / 2R . t = 2 m/s2 / 0,2 m . √10 sec => ω = 10√10 rad/sec
(Δ) υΚ = αΚ . t = 2 m/s2 . 10½ sec = 2√10 m/sec
υ = ω . 2R + υΚ = 10 . 10½ . 2 . 0,1 + 2 . 10½ = 4√10 m/s
12.
13. Η ομογενής ράβδος του σχήματος έχει βάρος w = 10 N και μήκος ℓ = 4 m. Το ένα της άκρο αρθρώνεται σε κατακόρυφο τοίχο και το άλλο της άκρο κρέμεται από κατακόρυφο σχοινί με αποτέλεσμα να ισορροπεί οριζόντια.
α) Να βρεθεί η τάση του νήματος.
β) Να βρεθεί η δύναμη που δέχεται η ράβδος από την άρθρωση.
Tη χρονική στιγμή t = 0, από το άκρο Α ξεκινάει να κυλίεται χωρίς να ολισθαίνει πάνω στη ράβδο ένας κύλινδρος βάρους w1 = 10 N με επιτάχυνση αcm = 1 m/s2 . Να υπολογίσετε :
γ) Την τάση του νήματος τη χρονική στιγμή t = √3 s.
δ) Τη γωνιακή ταχύτητα και τη θέση του κυλίνδρου, όταν η τάση του νήματος γίνει 10 Ν. (Δίνεται η ακτίνα του κυλίνδρου R = 0,1 m).
(ε) Εκφράστε την τάση του νήματος και την δύναμη που δέχεται η ράβδος από την άρθρωση συναρτήσει του χρόνου. [ α) 5N β) 5N γ) 8,75N δ) 20rad/s ] (α) ροπές ως προς Α : Στ = 0 => w . L/2 - T . L = 0 => T = w/2 = 5 N
(α) ροπές ως προς Α : Στ = 0 => w . L/2 - T . L = 0 => T = w/2 = 5 N
(β) ΣF = 0 => FA + T - w = 0 => FA + 5 - 10 = 0 => FA = 5 N
(γ) κίνηση κυλίνδρου : x = 0,5 . a . t2 = 0,5 . 1 . 3 = 1,5 m < 2 m = L/2
ροπές ως προς Α : Στ = 0 => w.L/2 + w1 .x - T.L = 0 => 10 . 2 + 10 . 1,5 - T . 4 = 0 => T = 35/4 N
(δ) T = 10 N ροπές ως προς Α : Στ = 0 => w . L/2 + w1 . x - T . L = 0 =>
=> 10 . 2 + 10 . x - 10 . 4 = 0 => x = 2 m ο κύλινδρος βρίσκεται στο μέσον της ράβδου
x = 0,5 . a . t2 => 2 = 0,5 . 1 . t2 => t = 2 sec υ = α t = 1 . 2 = 2 m/s
υ = ω R => ω = υ / R = 2 / 0,1 = 20 rad/s
(ε) ροπές ως προς Α : Στ = 0 => w . L/2 + w1 . x - T . L = 0 =>
=> T . L = w . L/2 + w1 . 0,5 . a . t2 => T . 4 = 10 . 2 + 10 . 0,5 . 1 . t2 => T = 5 + 5/4. t2
ΣF = 0 => FA + T - w - w1 = 0 => FA = w + w1 - T = 10 + 10 - ( 5 + 5/4. t2 ) => FA = 15 - 5/4. t2
για x = L => 0,5 . a . t2 = L => 0,5 . 1. t2 = 4 => t2 = 8 => t = 2√2 sec
T = 5 + 5/4. t2 FA = 15 - 5/4. t2 0 < t < 2√2 sec
14. Ο τροχός του σχήματος, βάρους w = 100 N, ισορροπεί πάνω σε κεκλιμένο επίπεδο γωνία κλίσης θ = 60° με τη βοήθεια του οριζόντιου νήματος ΒΓ.
α) Να αποδείξετε ότι το κεκλιμένο επίπεδο δεν είναι λείο.
β) Να υπολογίσετε τις δυνάμεις που ασκούνται στον τροχό. [ 100 √3/3 Ν, 100 Ν ]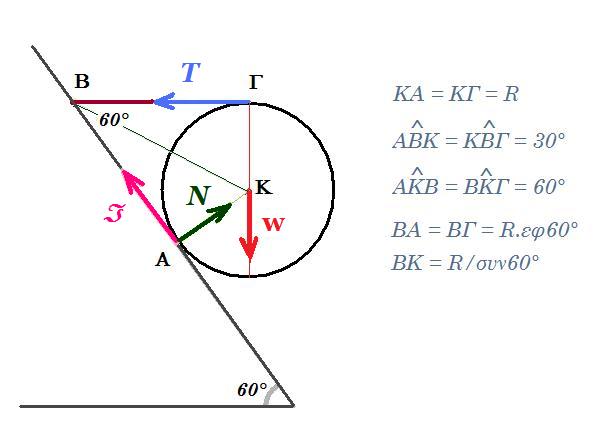
ροπές ως προς Α: w R ημ60° = Τ .(R + R συν60°) => 100 √3/2 = Τ (1 + 0,5) => Τ = 100√3/3 Ν
ροπές ως προς Β : w . (ΒΓ) = Ν . (ΒΑ) => Ν = w = 100 N
ροπές ως προς Κ : Τ . (ΚΓ) = T(A) . (ΚΑ) => δύναμη τριβής : T(A) = T = 100√3/3 Ν
15. Η διπλή τροχαλία του σχήματος αποτελείται από δύο ομογενείς ομόκεντρους δίσκους με ακτίνες R και 2R, που είναι συγκολλημένοι μεταξύ τους ώστε να περιστρέφονται ως ένα στερεό σώμα με μάζα Μ. Η τροχαλία μπορεί να περιστρέφεται χωρίς τριβές γύρω από σταθερό οριζόντιο άξονα κάθετο στο επίπεδο των δίσκων, ο οποίος διέρχεται από το κέντρο τους Ο. Στα αυλάκια των δίσκων έχουμε τυλίξει πολλές φορές αβαρή και μη εκτατα νήματα, στα ελεύθερα άκρα των οποίων κρέμονται σώματα Σ1 και Σ2 με μάζες m1 και m2 ( m2 > 2m1 ) αντίστοιχα. Αρχικά το σύστημα << τροχαλία - σώματα >> συγκρατείται ακίνητο με τα κέντρα μάζας των δύο σωμάτων να απέχουν κατακόρυφη απόσταση h. 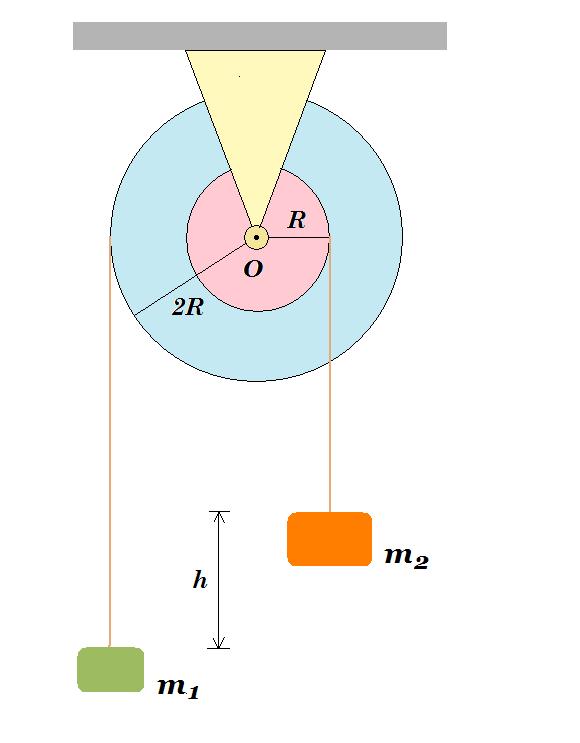 Κάποια στιγμή αφήνουμε το σύστημα ελεύθερο να κινηθεί, οπότε η τροχαλία αρχίζει να περιστρέφεται χωρίς τα νήματα να ολισθαίνουν στα αυλάκια των δίσκων. Η μετατόπιση του σώματος Σ2 μέχρι να φθάσει στο ίδιο οριζόντιο επίπεδο με το Σ1 ισούται με :
Κάποια στιγμή αφήνουμε το σύστημα ελεύθερο να κινηθεί, οπότε η τροχαλία αρχίζει να περιστρέφεται χωρίς τα νήματα να ολισθαίνουν στα αυλάκια των δίσκων. Η μετατόπιση του σώματος Σ2 μέχρι να φθάσει στο ίδιο οριζόντιο επίπεδο με το Σ1 ισούται με :
(α) h/2 (β) h/3 (γ) 2 h/3
Υπολογίστε την γωνιακή επιτάχυνση της τροχαλίας αν η ροπή αδράνειας ως προς το κέντρο της Ο είναι Ι = Μ.R2 .
m2 . g - T2 = m2 . a2 α2 = αγων . R m2 . g - T2 = m2 . αγων . R (1)
T1 - m1 . g = m1 . a1 α1 = αγων . 2R 2.T1 - 2.m1 .g = 2 . m1 . αγων . 2R (2)
T2 . R - T1 . 2R = I . aγων T2 - 2.T1 = I/R . aγων (3)
m2 . g - T2 + 2.T1 - 2.m1 .g + T2 - 2.T1 = m2 . αγων . R + 2 . m1 . αγων . 2R + I/R . aγων =>
(1) + (2) + (3) => m2 . g - 2.m1 .g = ( m2 . R + 4 . m1 . R + I/R ) . aγων =>
=> aγων = ( m2 - 2.m1 ) . g / ( m2 .R + 4 .m1 .R + I/R ) I = M.R2
=> aγων = ( m2 - 2.m1 ).g / ( m2 + 4 .m1 + M ).R
y1 = ½ . α1 . t2
y2 = ½ . α2 . t2 y1 / y2 = a1 / a2 = 2
h = y1 + y2 = 2 . y2 + y2 = 3 . y2 => y2 = h/3
16. Το στερεό σώμα κυκλικής διατομής έχει εξωτερική ακτίνα R = 0,2 m & μάζα m = 4 kg. Η ροπή αδράνειας του στερεού ως προς άξονα που διέρχεται από το κέντρο μάζας του είναι Ιcm = ½ m R2. Στο σώμα υπάρχει εσωτερικό αυλάκι με ακτίνα r = 0,1 m. Το στερεό βρίσκεται πάνω σε κεκλιμένο επίπεδο γωνίας κλίσης φ = 30°. Λεπτό αβαρές νήμα είναι τυλιγμένο στο εσωτερικό αυλάκι και δεν ολισθαίνει σε όλη τη διάρκεια του φαινομένου που ακολουθεί. Στην άκρη του νήματος που παραμένει συνεχώς παράλληλο με το κεκλιμένο επίπεδο ασκείται σταθερή δύναμη παράλληλη με το κεκλιμένο επίπεδο μέσω της οποίας ελέγχουμε την κίνηση του σώματος. 
Δ1. Υπολογίστε το μέτρο της δύναμης F ώστε το στερεό να ισορροπεί ακίνητο πάνω στο κεκλιμένο επίπεδο.
Δ2. Αυξάνουμε το μέτρο της δύναμης F κατά 30% και το στερεό αρχίζει να κυλίεται χωρίς να ολισθαίνει. Υπολογίστε το μέτρο της επιτάχυνσης του κέντρου μάζας του στερεού και το μέτρο του ρυθμού μεταβολής της στροφορμής του.
Δ3. Τη στιγμή t όπου το στερεό έχει μετατοπιστεί κατά Δx = 2 m από την αρχική του θέση υπολογίστε το μέτρο της ταχύτητας του κέντρου μάζας του.
Δ4. Πόση είναι η κινητική ενέργεια του στερεού λόγω περιστροφής και ποιος είναι ο ρυθμός μεταβολής της στροφικής κινητικής ενέργειας του τη στιγμή t ;
Δ5. Υπολογίστε το έργο που παράγεται από την δύναμη F από την αρχή της διαδικασίας έως την στιγμή t.
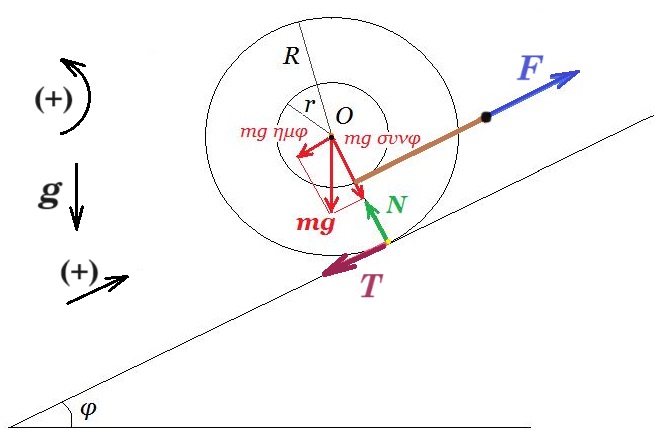
Δ1.
ΣF = 0 => F - T - m g ημφ = 0 (1) ημφ = ημ30° = 0,5
Στ(Ο) = 0 => F r = T R => T = F r / R => T = F 0,1 / 0,2 = F / 2 (2)
(1), (2) => F - F/2 = m g ημφ => F/2 = 4 10 0,5 => F = 40 N
Δ2.
ΣF = m a => F - T - m g ημφ = m a (3) ημφ = ημ30° = 0,5
Στ(Ο) = I(Ο) aγων => T R - F r = ½ m R2 aγων aγων = a / R
=> T R - F r = ½ m R a => T = F r/R + ½ m a = 52 0,1/0,2 + 0,5 4 a => T = 26 + 2 a (4)
(3) , (4) => 52 - ( 26 + 2 a ) - 4 10 0,5 = 4 a => 52 - 26 - 2 a - 20 = 4 a => a = 1 m/s2
ΔL /Δt = I aγων = ½ m R2 aγων = ½ m R a = ½ 4 0,2 1 = 0,4 Nm
Δ3.
x = ½ a t2 => 2m = 0,5 1m/s2 t2 => t = 2 sec
vcm = a t = 1m/s2 2s = 2 m/s
ω = vcm / R = 2 / 0,2 = 10 rad/s
aγων = a / R = 1 / 0,2 = 5 rad/s2 θ = ½ αγων t2 = ½ 5 22 = 10 rad
l = θ r = 10 rad 0,1 m = 1 m
Δ4.
Kπεριστροφής = ½ I(O) ω2 = ½ ½ m R2 (aγων t) 2 = ½ ½ 4 0,22 (5 2)2 = 4 Joule
dK / dt = I(O) ω aγων = ½ m R2 ω aγων = ½ 4 0,22 10 5 = 4 J/s
Δ5.
Kμεταφοράς = ½ m v2 = ½ 4 22 = 8 J Kολική = 4 J + 8 J = 12 J
U = m g h = m g x ημ30° = 4 10 2 ½ = 40 J WF = F θ r = 52 J 10 rad 0,1 m = 52 J
WF = Kολική + U = 4 J + 8 J + 40 J = 52 J
17. Oμογενής και συμπαγής δίσκος ακτίνας R και μάζας Μ συνδέεται από το κέντρο μάζας του με αβαρές ελατήριο σταθεράς k έτσι ώστε να μπορεί να κυλίεται χωρίς να ολισθαίνει γύρω από άξονα που διέρχεται από το κέντρο μάζας του και είναι κάθετος στο επίπεδο του. Η ροπή αδράνειας του δίσκου ως προς άξονα που διέρχεται από το κέντρο μάζας του είναι Ιcm = ½ m R2. Το σύστημα αφήνεται χωρίς αρχική ταχύτητα από μια θέση όπου το ελατήριο έχει επιμηκυνθεί κατά Α. Τη χρονική στιγμή που το ελατήριο έχει το φυσικό του μήκος το κέντρο μάζας έχει ταχύτητα μέτρου :
(α) Α ( 2k/3Μ )½ (β) Α ( k/Μ )½ (γ) Α ( 3k/2Μ )½ 
κύλιση χωρίς ολίσθηση : v = R ω => a = R αγων
Στ(Ο) = Ι(O) αγων => Τ R = ½ m R2 αγων => Τ = ½ m R αγων = ½ m α
ΣFx = m a => Fελατ - Τ = m a => k x - ½ m R α = m a => k x = 3/2 m α => α = 2k/3m x
ω2 = 2k/3m x(t) = A ημ(ωt + 3π/2) υ(t) = ω A συν(ωt + 3π/2) α(t) = - ω2 A ημ(ωt + 3π/2)
εφαρμογή : A = 0,1 m k = 300 N/m m = 2 kg R = 0,5 m
ω2 = 2k/3m = (2 300) / (3 2) = 100 => ω = 10 rad/s
x(t) = A ημ(ωt + 3π/2) => x(t) = 0,1 ημ(10t + 3π/2)
v(t) = 1 συν(10t + 3π/2) α(t) = - 10 ημ(10t + 3π/2) F(t) = m a = - 20 ημ(10t + 3π/2)
ΣF = m a = Fελατ - Τ => Fελατ = m a + ½ m a = 3/2 m a =>
=> Fελατ (t) = 3/2 ( - 20 ημ(10t + 3π/2) ) = - 30 ημ(10t + 3π/2)
18. ΟΕΦΕ 2012 Δ Διπλή τροχαλία αποτελείται από δύο ομογενείς δίσκους με ακτίνες r = 0,1 m και R = 0,2 m και μάζες m = 2 kg και Μ = 4 kg αντίστοιχα. Οι δύο δίσκοι συνδέονται μεταξύ τους έτσι ώστε να περιστρέφονται ως ένα σώμα χωρίς τριβές γύρω από σταθερό άξονα που διέρχεται από το κέντρο τους και είναι κάθετος στο επίπεδό τους. 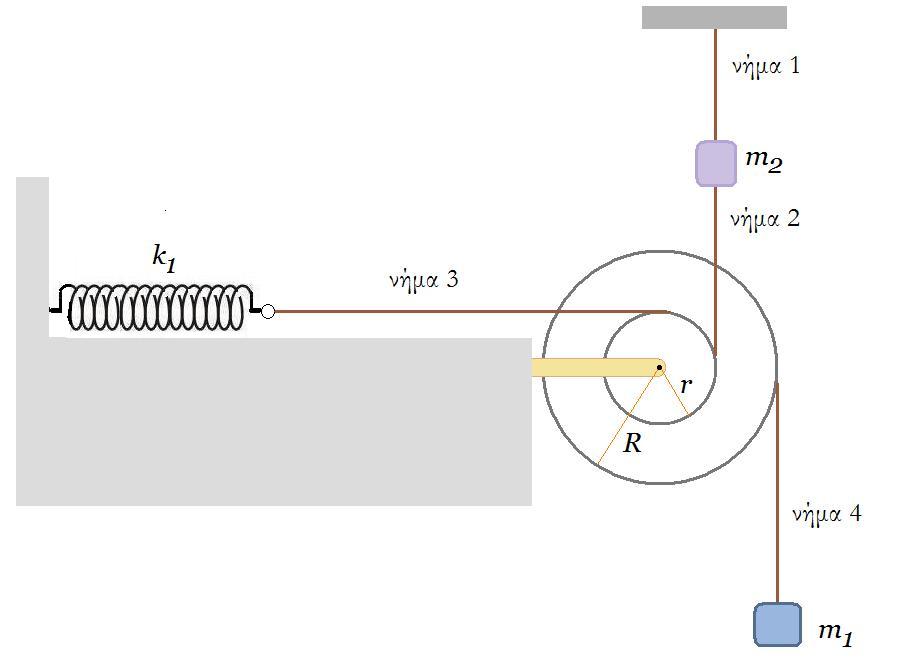
Στο αυλάκι του μεγάλου δίσκου της τροχαλίας έχουμε τυλίξει αβαρές και μη εκτατό νήμα (4) στο ελεύθερο άκρο του οποίου έχουμε δέσει σώμα μάζας m1 = 1 kg. Στο αυλάκι του μικρού δίσκου της τροχαλίας έχουμε τυλίξει δύο αβαρή και μη εκτατά νήματα (3) και (2). Στο ελεύθερο άκρο του οριζοντίου νήματος (3) έχουμε δέσει το ένα άκρο οριζόντιου ιδανικού ελατηρίου σταθεράς k = 200 N/m του οποίου το άλλο άκρο είναι δεμένο σε σταθερό σημείο. Στο ελεύθερο άκρο του κατακόρυφου νήματος (2) έχουμε δέσει σώμα μάζας m2 = 0,5 kg το οποίο είναι δεμένο και με αβαρές ελαστικό κατακόρυφο νήμα (1) από σταθερό σημείο της οροφής. Το μέτρο της δύναμης στο νήμα (1) είναι ανάλογο της επιμήκυνσης σύμφωνα με τη σχέση : F = 100 Δl. Το σύστημα ισορροπεί με το νήμα (1) να είναι επιμηκυμένο κατά Δl = 0,2 m.
Δ1. Βρείτε την παραμόρφωση του ελατηρίου.
Κάποια στιγμή κόβουμε το νήμα (2). Υπολογίστε :
Δ2. τη γωνιακή επιτάχυνση της τροχαλίας αμέσως μετά το κόψιμο του νήματος (2)
Δ3. τη μέγιστη τιμή της κινητικής ενέργειας του συστήματος ( τροχαλία - μάζα m1 )
Δ4. το διάστημα που θα διανύσει το σώμα μάζας m1 μέχρι να μηδενισθεί η ταχύτητά του για πρώτη φορά μετά το κόψιμο του νήματος (2)
Δ5. το διάστημα που θα διανύσει το σώμα μάζας m2 μέχρι να μηδενισθεί η ταχύτητά του για πρώτη φορά μετά το κόψιμο του νήματος (2).
Δ1. ισορροπία Σ1 : m1 g = T4 => T4 = 10 N
ισορροπία Σ2 : m2 g + T2 = T1 = F = 100 Δl => 0,5 10 + T2 = 100 0,2 => T2 = 15 N
ισορροπία τροχαλίας : ( Τ3 + Τ2 ) r = T4 R => ( Τ3 + 15 ) 0,1 = 10 0,2 => T3 = 5 N
ελατήριο σε επιμήκυνση : Τ3 = Fελατ = k x0 => x0 = 5 / 200 = 0,025 m
Δ2.
ροπή αδράνειας της τροχαλίας ως προς το κέντρο της Ο : Ι(Ο) = ½ m r2 + ½ M R2 =
= ½ 2 0,12 + ½ 4 0,22 = 0,01 + 2 0,04 => Ι(Ο) = 0,09 kg m2
ΣF(1) = m1 α1 => m1 g - T4 = m1 α = m1 αγων R α = αγων R
m1 g - T4 = m1 αγων R => 10 - T4 = 1 0,2 αγων (1)
όταν κόβεται το νήμα (2) η δύναμη ελατηρίου είναι 5 Ν = Τ3
Στ(Ο) = Ι(Ο) αγων => T4 R - Τ3 r = Ι(Ο) αγων => T4 0,2 - 5 0,1 = 0,09 αγων =>
T4 - 2,5 = 0,45 αγων (2)
(1) + (2) => 10 - 2,5 = 0,65 αγων => αγων = 7,5 / 0,65 = 750/65 = 150/13 rad/s2
Δ3. καθώς κατέρχεται το σώμα Σ1 :
m1 g - T4 = m1 α => 10 - T4 = α (3)
T4 R - Τ3 r = Ι(Ο) αγων => T4 R - k x r = Ι(Ο) α / R => T4 0,2 - 200 x 0,1 = 0,09 α / 0,2 => T4 - 100 x = 0,45 α (4)
(3) + (4) => 10 - 100 x = 1,45 a καθώς κατέρχεται το σώμα Σ1 το ελατήριο επιμηκύνεται οπότε η επιτάχυνση α μειώνεται μέχρι να μηδενισθεί, τότε έχουμε μέγιστη ταχύτητα διότι α = 0 => dv/dt = 0 => v(t)' = 0 => v = max ακρότατο αυτό γίνεται όταν 10 - 100 x1 = 0 => x1 = 0,1 m τότε η δυναμική ενέργεια του ελατηρίου θα είναι : U = ½ k x12 = ½ 200 0,12 = 1 J η αρχική δυναμική ενέργεια του ελατηρίου : Uαρχ = ½ k x02 = ½ 200 0,0252 = 0,0625 J
η μετατόπιση του άκρου του ελατηρίου είναι : x1 - x0 = 0,1 m - 0,025 m = 0,075 m
το νήμα (3) τυλίγεται κατά 0,075 m, η τροχαλία στρέφεται κατά γωνία θ = (x1 - x0) / r = 0,075 / 0,1 = 0,75 rad, το νήμα (4) ξετυλίγεται κατά s = θ R = 0,75 rad 0,2 m = 0,15 m τότε το σώμα Σ1 μετατοπίζεται κατά : h = s = 0,015 m
½ k x02 + m1 g h = ½ k x12 + ½ m1 v2 + ½ Ι(Ο) ω2 a = 0 => aγων = 0 => ω = 0
0,0625 J + 1 10 0,15 = 1 + ½ m1 v2
0,0625 J + 1,5 = 1 + ½ m1 v2
0,5625 J = ½ m1 v2
Δ4.
½ k x02 + m1 g h = ½ k x2 + ½ m1 v2 + ½ Ι(Ο) ω2
½ k x02 + m1 g 2 ( x - x0 ) = ½ k x2
0,0625 + 10 2 ( x - 0,025 ) = ½ 200 x2
0,0625 + 20 x - 0,5 = 100 x2
100 x2 - 20 x + 0,4375 = 0 Δ = 400 - 4 100 0,4375 = 225 = 152
x1,2 = ( - β ± Δ½ ) / 2α = ( 20 ± 15 ) / 200 = 0,175 m ή 0,025 m αρχική επιμήκυνση ελατηρίου
το σώμα Σ1 μετατοπίστηκε : h = 2 ( x - 0,025 ) = 2 ( 0,175 - 0,025 ) = 0,3 m
Δ5. ½ 100 Δl2 = m2 g h => ½ 100 0,22 = 0,5 10 h => 4 = 10 h => h = 0,4 m
Δ3. άλλος τρόπος
½ k x02 + m1 g h = ½ k x2 + ½ m1 v2 + ½ Ι(Ο) ω2 ω = v/R h = 2 ( x - x0 )
½ k x02 + m1 g 2 ( x - x0 ) = ½ k x2 + ½ m1 v2 + ½ Ι(Ο) (v/R)2
200 0,000625 + 40 ( x - 0,025 ) = 200 x2 + v2 + 0,09 v2 / 0,04
0,125 + 40 x - 1 = 200 x2 + v2 + 2,25 v2
- 0,875 + 40 x = 200 x2 + 3,25 v2
200 x2 - 40 x + 3,25 v2 + 0,875 = 0
Δ = 1600 - 4 200 ( 3,25 v2 + 0,875 ) = 1600 - 2600 v2 - 700 = 900 - 2600 v2
Δ > 0 => 900 - 2600 v2 > 0 => 900 / 2600 > v2 vmax2 = 9/26
Κ = ½ m1 v2 + ½ Ι(Ο) (v/R)2 = ½ 1 9/26 + ½ 0,09 9/26 / 0,04 =
= 9/26 ( 0,5 + 1,125 ) = 0,5625 J μέγιστη κινητική ενέργεια του συστήματος ( τροχαλία - μάζα m1 )
3,25 v2 + 0,875 = 3,25 9/26 + 0,875 = 1,125 + 0,875 = 2
200 x2 - 40 x + 2 = 0 => 100 x2 - 20 x + 1 = 0 Δ = 400 - 400 = 0
x = 20 / 200 = 0,1 m επιμήκυνση ελατηρίου
ισορροπία σώματος Σ2 : Δl = 0,3 m m2 = 1 kg
m2 g = F = 100 x0 => x0 = m2 g / 100 = 1 10 / 100 => x0 = 0,1 m
διατήρηση ενέργειας στη θέση ισορροπίας (Β) :
½ 100 Δl2 = ½ 100 x0 2 + ½ m2 υ2 + m2 g ( Δl - x0 )
½ 100 0,32 = ½ 100 0,12 + ½ 1 υ2 + 1 10 ( 0,3 - 0,1 )
½ 9 = ½ 1 + ½ 1 υ2 + 10 0,2
9 = 1 + υ2 + 4
υ2 = 4 => υ = 2 m/s
όταν διέρχεται τοσώμα Σ2 από τη θέση ισορροπίας του (Β) έχει ταχύτητα υ = 2 m/s
διατήρηση ενέργειας από την κατώτατη θέση (Α) έως την ανώτατη θέση (Δ) :
½ 100 Δl2 = m2 g h => 100 0,32 = 2 1 10 h => 9 = 20 h => h = 0,45 m
το σώμα από την κατώτατη θέση φθάνει σε ύψος h = 0,45 m
όταν διέρχεται από τη θέση (Γ) όπου το ελαστικό νήμα (1) έχει το φυσικό του μήκος :
½ 100 Δl2 = m2 g Δl + ½ m2 u2
½ 100 0,32 = 1 10 0,3 + ½ 1 u2
½ 9 = 3 + ½ u2 => 9 = 6 + u2 => u = 3½ m/s
μετά το Σ2 θα κάνει κατακόρυφη βολή προς τα πάνω :
v = u - g t => 0 = u - g t => t = u / g = 3½ / 10 s
h' = ½ g t2 = ½ 10 3/100 => h' = 0,15 m
ταλάντωση του Σ2 : πλάτος Α = Δl - x0 = 0,3 - 0,1 => A = 0,2 m
ω2 = 100 / m2 = 100 / 1 = 100 => ω = 10 rad/s
T = 2π/ω = 2π / 10 => Τ = π / 5 s => T/4 = π / 20 s
½ 100 Α2 = ½ m2 υ2 => 100 0,22 = 1 υ2 => υ2 = 4 => υ = 2 m/s
x = A ημ(ωt + π/2) => x(t) = 0,2 ημ(10 t + π/2) υ(t) = 2 συν(10 t + π/2)
α(t) = - 20 ημ(10 t + π/2) F(t) = m2 a(t) = - 20 ημ(10 t + π/2)
ΣF(t) = m2 a(t) => m2 g + Fελατ = - 20 ημ(10 t + π/2) => Fελατ = - m2 g - 20 ημ(10 t + π/2)
=> Fελατ(t) = - 10 - 20 ημ(10 t + π/2)
x = 0,2 ημ(10 t + π/2) => - 0,1 = 0,2 ημ(10 t + π/2) =>
=> ημ(10 t + π/2) = - ½ = ημ(π+π/6) = ημ(2π-π/6) => 10 t + π/2 = 2Ν π + π+π/6 ή 10 t + π/2 = 2Ν π + 2π-π/6
10 t + π/2 = 2Ν π + π+π/6 => 10 t = 2Ν π + π/2 + π/6
Ν = 0 10 t = 2π/3 => t = π/15 s
10 t + π/2 = 2Ν π + 2π-π/6 => 10 t = 2Ν π + 3π/2 - π/6
N = 0 10 t = 3π/2 - π/6 = 4π/3 => t = 2π/15 s
x(π/15) = 0,2 ημ(10 π/15 + π/2) = 0,2 ημ(2π/3 + π/2) = 0,2 ημ(7π/6) = 0,2 ημ(π + π/6) = 0,2 (-½) = - 0,1 m θέση (Γ) το ελατήριο έχει το φυσικό του μήκος
Fελατ(π/15) = - 10 - 20 ημ(10 π/15 + π/2) = - 10 - 20 ημ(2π/3 + π/2) = - 10 - 20 ημ(7π/6) = 0
υ(π/15) = 2 συν(10 π/15 + π/2) = 2 συν(2π/3 + π/2) = 2 συν(π + π/6) = 2 (- 3½/2) = - 3½ m/s το σώμα ανέρχεται
x(2π/15) = 0,2 ημ(10 2π/15 + π/2) = 0,2 ημ(4π/3 + π/2) = 0,2 ημ(11π/6) = 0,2 (-½) = - 0,1 m θέση (Γ) το ελατήριο έχει το φυσικό του μήκος
Fελατ(2π/15) = - 10 - 20 ημ(10 2π/15 + π/2) = - 10 - 20 ημ(4π/3 + π/2) = - 10 - 20 ημ(11π/6) = 0
υ(2π/15) = 2 συν(10 2π/15 + π/2) = 2 συν(4π/3 + π/2) = 2 συν(11π/6) = 2 (+3½/2) = +3½ m/s το σώμα κατέρχεται
από την κατώτατη θέση (Α) σε χρόνο T/4 = π / 20 s διέρχεται από τη θέση ισορροπίας (Β) με ταχύτητα υ(π/20) = 2 συν(10 π/20 + π/2) = 2 συν(π/2 + π/2) = 2 συν(π) => υ = - 2 m/s ( (-) διότι ανέρχεται ), μετά διέρχεται από τη θέση (Γ) με ταχύτητα u = - 3½ m/s σε χρόνο π/15 s
και φθάνει στην ανώτατη θέση (Δ) μετά από 3½/10 s
19. Ομογενής δίσκος μάζας Μ = 3,6 kg και ακτίνας R = 0,2 m μπορεί να περιστρέφεται χωρίς τριβές γύρω από σταθερό οριζόντιο άξονα που περνά από το κέντρο μάζας του και είναι κάθετος στο επίπεδό του. Αρχικά ο δίσκος είναι ακίνητος. Σφαίρα αμελητέων διαστάσεων μάζας m = 0,2 kg κινείται οριζόντια στο επίπεδο του δίσκου με ταχύτητα υ0 και ενσωματώνεται ακαριαία στο ανώτερο σημείο του δίσκου. Η γωνιακή ταχύτητα του συστήματος αμέσως μετά την κρούση είναι ω = 20 rad/s. 
Υπολογίστε :
(α) την ροπή αδράνειας του συστήματος μετά την κρούση
(β) το μέτρο της ταχύτητας υ0 της σφαίρας
(γ) για πόσο χρόνο θα πρέπει σταθερή εφαπτομενική δύναμη F = 8 Ν να ασκείται στην περιφέρεια του δίσκου ώστε το σύστημα των δύο σωμάτων να ακινητοποιηθεί
(δ) την κινητική ενέργεια του συστήματος και τον ρυθμό μεταβολής της τη στιγμή t1 = 0,5s λόγω της επιδράσεως της δύναμης F.
ροπή αδράνειας του δίσκου ως προς τον άξονα περιστροφής : Ι = ½ Μ R2.
Iολ = ½ M R2 + m R2 = ½ 3,6 0,22 + 0,2 0,22 = 2 0,04 = 0,08 kg m2
Lπριν = Lμετά => m υ0 R = Ιολ ω => 0,2 υ0 0,2 = 0,08 20 => υ0 = 40 m/s
Στ(Ο) = Ιολ αγων = ΔL/Δt => F R = ΔL/Δt => Δt = ΔL / (F R) =>
=> Δt = ( Ιολ ω - 0 ) / (F R) => Δt = ( 0,08 20 ) / (8 0,2) = 1 s
αγων = Δω / Δt = (20 - 0) / 1 = 20 rad/s2
ω1 = ω0 - αγων t = 20 - 20 0,5 = 10 rad/s
Κ = ½ Ιολ ω12 = ½ 0,08 102 = 4 J
dK/dt = Ιολ ω1 αγων = 0,08 10 20 = 16 J/s
20. ΟΕΦΕ 2004 H τροχαλία του σχήματος είναι ομογενής μάζας Μ = 4 kg και ακτίνας R = 0,2 m. Τα σώματα Σ1 και Σ2 έχουν μάζες m1 = 4 kg και m2 = 2 kg και το σχοινί που τα συγκρατεί έχει αμελητέα μάζα. Το σώμα Σ2 είναι κολλημένο με άλλο σώμα Σ3 μάζας m3 = 1 kg. Το σώμα Σ3 είναι στερεωμένο στο άκρο κατακόρυφου ελατηρίου σταθεράς k = 100 N/m το άλλο άκρο του οποίου είναι στερεωμένο στο έδαφος. Το σύστημα αρχικά ισορροπεί ακίνητο. Τη στιγμή t = 0 τα σώματα Σ1 και Σ2 αποκολλούνται.
(α) Γράψτε την εξίσωση της απομάκρυσης της ταλάντωσης που θα εκτελέσει το σώμα Σ3 .
(β) Υπολογίστε την γωνιακή ταχύτητα της τροχαλίας τη στιγμή που το σώμα Σ3 διέρχεται από τη θέση ισορροπίας του για πρώτη φορά.
(γ) Υπολογίστε την στροφορμή του συστήματος της τροχαλίας και των σωμάτων Σ1 και Σ2 τη στιγμή t = 2 s.
H τριβή ανάμεσα στην τροαλία και το σχοινί είναι αρκετά μεγάλη ώστε δεν παρατηρείται ολίσθηση. Τα σώματα Σ1 , Σ2 και Σ3 είναι μικρών διαστάσεων.
(α) ισορροπία Σ1 : m1 g = T => 4 10 = T => T = 40 N
ισορροπία Σ2,3 : ( m2 + m3 ) g + Fελατ = T => ( 2 + 1 ) 10 + Fελατ = 40 => Fελατ = 10 Ν => Fελατ = k Δl => Δl = 10 / 100 = 0,1 m επιμήκυνση
τα σώματα Σ2 και Σ3 αποκολλούνται :
ισορροπία Σ3 : m3 g = k x3 => x3 = m3 g / k = 1 10 / 100 => x3 = 0,1 m συσπείρωση
πλάτος ταλάντωσης Σ3 : Α = Δl + x3 = 0,1 m + 0,1 m = 0,2 m
ω2 = k / m3 = 100 / 1 => ω = 10 rad/s x(t) = 0,2 ημ(10t + π/2)
υ(t) = 2 συν(10t + π/2) α(t) = - 20 ημ(10t + π/2) F(t) = m3 a(t) = - 20 ημ(10t + π/2)
(β) t = T/4 = 2π / 40 s = π/20 s επειδή m1 > m2 το Σ1 κατέρχεται το Σ2 ανέρχεται και η τροχαλία στρέφεται δεξιόστροφα
m1 g - T1 = m1 α => 4 10 - T1 = 4 α => 40 - T1 = 4 α (1)
T2 - m2 g = m2 α => T2 - 2 10 = 2 α => T2 - 20 = 2 α (2)
Στ(Ο) = Ι(Ο) αγων => ( T1 - T2 ) R = ½ Μ R2 αγων => T1 - T2 = ½ 4 α (3) α = αγων R
(1)+(2)+(3) => 40 - 20 = 4α + 2α + 2α => α = 2,5 m/s2 aγων = α / R = 2,5 / 0,2 = 12,5 rad/s2
ω = aγων t = 12,5 rad/s2 π/20 s => ω = 5π/8 rad/s
(γ) L = I ω = ( m1 R2 + m2 R2 + ½ Μ R2 ) aγων t = ( 4 0,22 + 2 0,22 + ½ 4 0.22 ) 12,5 2 = 8 0,04 25 => L = 8 kg m2 / s
21. ΟΕΦΕ 2006 H ομογενής ράβδος ΟΑ του σχήματος έχει μήκος L = 1 m μάζα m = 3 kg και μπορεί να περιστρέφεται σε κατακόρυφο επίπεδο χωρίς τριβές γύρω από οριζόντιο ακλόνητο άξονα που περνά από το άκρο της Ο και είναι κάθετος σε αυτή.
Α. Η ράβδος ισορροπεί σε οριζόντια θέση με τη βοήθεια δύναμης F1 που ασκείται στο άκρο Α κάθετα στη ράβδο.
Να υπολογίσετε το μέτρο της F1 και το μέτρο της δύναμης που δέχεται η ράβδος από τον άξονα περιστροφής.
Β. Ασκώντας στο άκρο Α αντί της δύναμης F1 μια δύναμη F2 σταθερού μέτρου και διαρκώς κάθετη στη ράβδο η ράβδος ανέρχεται και περνά από την ανώτερη θέση της με γωνιακή ταχύτητα ω0 = 30½ rad/s. Τη στιγμή αυτή η F2 παύει να ασκείται στη ράβδο. Υπολογίστε το μέτρο της δύναμης F2.
Γ. Τη στιγμή κατά την οποία η ράβδος διέρχεται από την οριζόντια θέση δτη διάρκεια της καθόδου της να υπολογίσετε :
(α) το ρυθμό μεταβολής της στροφορμής της ράβδου ως προς τον άξονα περιστροφής της.
(β) το ρυθμό μεταβολής της κινητικής ενέργειας της ράβδου.
Δ. Σημειακή μάζα m1 = 0,1 kg κινούμενη οριζόντια με ταχύτητα μέτρου υ1 = 100 m/s συγκρούεται πλαστικά με την ράβδο τη στιγμή που διέρχεται από το κατώτερο σημείο της τροχιάς της. Πόσο πρέπει να απέχει το σημείο σύγκρουσης από τον άξονα περιστροφής της ράβδου ώστε αυτή να ακινητοποιηθεί μετά την σύγκρουση;
ροπές ως προς Ο : m g L/2 = F1 L => F1 = m g /2 = 3 10 / 2 = 15 N
ΣF = 0 => m g - F1 + F(O) = 0 => 30 - 15 + F(O) = 0 => F(O) = - 15 N
κατεύθυνση κατακόρυφη προς τα πάνω με μέτρο 15 Ν
WF2 = ½ I(Ο) ω2 + m g L/2 => F2 s = ½ 1/3 m L2 ω0 2 + m g L/2
=> F2 π/2 L = ½ 1/3 m L2 ω0 2 + m g L/2 => F2 π/2 = ½ 1/3 m L ω02 + m g 1/2
=> F2 π/2 = ½ 1/3 3 1 30 + 30 1/2 = 30 => F2 = 60/π N
Στ(Ο) = Ι(Ο) αγων => m g L/2 = 1/3 m L2 αγων => 15 rad/s2 = αγων
½ I(Ο) ω0 2 + m g L/2 = ½ I(Ο) ω1 2 => ½ 1/3 m L2 ω0 2 + m g L/2 = ½ 1/3 m L2 ω1 2 => ω1 2 = ω0 2 + 3g/L = 30 + 30 = 60 => ω1 = 60½ rad/s
dK/dt = I(Ο) ω1 αγων = 1/3 m L2 ω1 αγων = 1/3 3 12 60½ 15 = 15 60½ J/s
½ I(Ο) ω1 2 + m g L/2 = ½ I(Ο) ω2 2 => ½ 1/3 m L2 ω1 2 + m g L/2 = ½ 1/3 m L2 ω2 2 => ω2 2 = ω1 2 + 3g/L = 60 + 30 = 90 => ω2 = 90½ rad/s
m1 v1 r - I(Ο) ω2 = 0 => 0,1 100 r - 1 90½ = 0 => r = 90½ /10 m
22. ΟΕΦΕ 2007 Σώμα Σ1 μάζας m1 = 2 kg μπορεί να κινείται κατακόρυφα προς τα κάτω έτσι ώστε μέσω της τροχαλίας μάζας m = 2 kg να ξετυλίγεται το σχοινί που είναι τυλιγμένο γύρω από τον κύλινδρο ακτίνας R = 0,2 m που μπορεί να περιστρέφεται με τον άξονα του κατακόρυφο. Κατακόρυφη αβαρής ράβδος αμελητέας ακτίνας διέρχεται από τον άξονα του κυλίνδρου και στο επάνω άκρο της στερεώνεται από το μέσο της δεύτερη οριζόντια αβαρής ράβδος μήκους l = 1 m. Δύο μικροί δακτύλιοι Σ2 και Σ3 με αμελητέες διαστάσεις και ίσες μάζες m2 = m3 = 0,025 kg βρίσκονται στα άκρα της οριζόντιας ράβδου και συνδέονται μεταξύ τους μέσω αβαρούς νήματος με όριο θραύσης Τθρ = 25 Ν. Το όλο σύστημα μπορεί να στρέφεται χωρίς τριβές σαν ενιαίο σώμα γύρω από άξονα που έχει τη διεύθυνση της κατακόρυφης ράβδου. Το νήμα που συνδέει τους δακτυλίους και το σχοινί που συνδέει το σώμα Σ1 με τον κύλινδρο παραμένουν διαρκώς τεντωμένα. Η τριβή ανάμεσα στη τροχαλία και το σχοινί είναι αρκετά μεγάλη ώστε να μην παρατηρείται ολίσθηση.
Να βρεθούν :
(α) η τάση του νήματος που ασκείται στο σώμα Σ1 αν η επιτάχυνση του είναι α = 4 m/s2
(β) η συχνότητα περιστροφής των δακτυλίων Σ2 και Σ3 μετά από χρονικό διάστημα 1,5π s από την έναρξή της περιστροφής τους
(γ) η ροπή αδράνειας του κυλίνδρου ως προς τον άξονα περιστροφής του συστήματος
(δ) η γωνία περιστροφής του κυλίνδρου από την έναρξη της περιστροφής του συστήματος μέχρι τη στιγμή που το νήμα που συνδέει τους δακτυλίους είναι έτοιμο να κοπεί.

m1 g - T1 = m1 a => 20 - T1 = 2 a (1) a = 4 m/s2 τότε T1 = 12 N
( T1 - T2 ) R1 = I(τροχ) aγων,1 => ( T1 - T2 ) R1 = ½ m R12 aγων,1 => T1 - T2 = ½ 2 R1 aγων,1
=> T1 - T2 = R1 aγων,1 = a (2) τότε Τ2 = Τ1 - α = 12 - 4 = 8 Ν
a = R1 aγων,1 = R aγων,2 => aγων,2 = α / R = 4 / 0,2 = 20 rad/s2 γωνιακή επιτάχυνση κυλίνδρου
τότε ωκυλίνδρου = aγων,2 t = 20 1,5 π => ωκυλίνδρου = 30 π rad/s f = ωκυλίνδρου / 2π = 15 Ηz
T2 R = I aγων,2 => T2 0,2 = [ m2 (L/2)2 + m3 (L/2)2 + Ι(Κ) ] aγων,2 =>
=> T2 0,2 = [ 2 0,025 0,52 + Ι(Κ) ] 20 => 8 = [ 0,0125 + Ι(Κ) ] 100 => 8 = 1,25 + Ι(Κ) 100 => Ι(Κ) = 0,0675 kg m2
Tθραύσεως = Fκεντρομόλος = m2 ω2 L/2 => 25 = 0,025 ω2 1/2 => ω2 = 2000 = ( 20 t )2 => t2 = 2000 / 400 = 5 => t = 5½ s τότε θ = ½ aγων,2 t2 = ½ 20 5 => θ = 50 rad
23. ΟΕΦΕ 2008 O αρχικά ακίνητος τροχός του σχήματος που βρίσκεται στη βάση κεκλιμένου επιπέδου ( θέση Α ) γωνίας κλίσεως 30° αποτελείται από ένα λεπτό ομογενή δακτύλιο μάζας 6 kg και ακτίνας 1 m και δύο λεπτές ομογενής ράβδους μήκους 2 m και μάζας 3 kg η κάθε μία που είναι τοποθετημένες κάθετα μεταξύ τους.
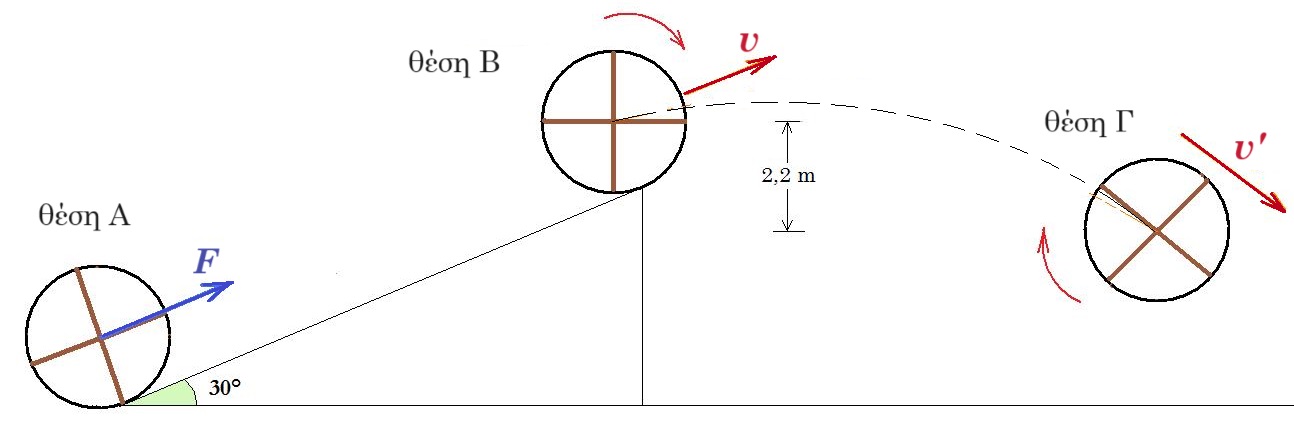 Τη στιγμή t =0 ασκούμε στο κέντρο μάζας Ο του τροχού σταθερή δύναμη F = 100 Ν παράλληλη στο κεκλιμένο επίπεδο και ο τροχός αρχίζει να κυλίεται χωρίς να ολισθαίνει ανερχόμενος στο κεκλιμένο επίπεδο. Όταν ο τροχός φθάσει στην κορυφή του κεκλιμένου επιπέδου ( θέση Β ) έχει εκτελέσει 12,5/π περιστροφές. Στη θέση Β καταργούμε την δύναμη F και ο τροχός στη συνέχεια εγκαταλείπει το κεκλιμένο επίπεδο διαγράφοντας καμπύλη τροχιά. Να υπολογίσετε :
Τη στιγμή t =0 ασκούμε στο κέντρο μάζας Ο του τροχού σταθερή δύναμη F = 100 Ν παράλληλη στο κεκλιμένο επίπεδο και ο τροχός αρχίζει να κυλίεται χωρίς να ολισθαίνει ανερχόμενος στο κεκλιμένο επίπεδο. Όταν ο τροχός φθάσει στην κορυφή του κεκλιμένου επιπέδου ( θέση Β ) έχει εκτελέσει 12,5/π περιστροφές. Στη θέση Β καταργούμε την δύναμη F και ο τροχός στη συνέχεια εγκαταλείπει το κεκλιμένο επίπεδο διαγράφοντας καμπύλη τροχιά. Να υπολογίσετε :
(α) Τη ροπή αδράνειας του τροχού ως προς τον άξονα που διέρχεται από το κέντρο μάζας Ο΄ και είναι κάθετος στο επίπεδο που ορίζει ο τροχός.
(β) Το μέτρο της στατικής τριβής που δέχεται που δέχεται ο τροχός από το κεκλιμένο επίπεδο.
(γ) Το ρυθμό μεταβολής της κινητικής ενέργειας του τροχού λόγω περιστροφικής κίνησης ακριβώς πριν αυτός χάσει την επαφή του με το κεκλιμένο επίπεδο ( θέση Β ).
(δ) Την ταχύτητα του κέντρου μάζας του τροχού τη στιγμή που διέρχεται από τη θέση Γ αν η κατακόρυφη μετατόπιση του κέντρου μάζας του τροχού από τη θέση Β μέχρι τη θέση Γ είναι 2,2 m προς τα κάτω.
R = L/2 = 1 m aγων = α / R = α / 1m
Ι(Ο) = Μ R2 + 2 1/12 m L2 = 6kg 1m2 + 2 1/12 3kg (2m)2 = 6 + 2 => Ι(Ο) = 8 kg m2
F - Mολική g ημ30° - Τ = Mολική α => 100 - 12 10 0,5 - Τ = 12 α => 40 - Τ = 12 α (1)
Τ R = I(O) aγων => Τ 1 = 8 α => Τ = 8 α (2)
(1) + (2) => 40 = 20 α => α = 2 m/s2 τότε T = 8 2 = 16 N
θ = Ν 2π => θ = 12,5/π 2π = 25 rad s = θ R = 25 m h = s ημ30° = 25 0,5 =12,5 m
F s = Mολική g h + ½ Mολική υ2 + ½ I(O) ω2
F s = Mολική g h + ½ Mολική ω2 R2 + ½ I(O) ω2
100 25 = 12 10 12,5 + ½ 12 ω2 12 + ½ 8 ω2
2500 = 1500 + 6 ω2 + 4 ω2
1000 = 10 ω2 => ω = 10 rad/s v = ω R = 10 1 = 10 m/s
ω = αγων t θ = ½ αγων t2 => θ = ½ ω t => t = 2 θ / ω = 2 25 / 10 = 5 s
αγων = ω / t = 10 / 5 = 2 rad/s2
K = 0,5 I(O) ω2 dK/dt = I(O) ω αγων = 8 10 2 = 160 J/s
το στερεό στον αέρα δεν δέχεται δύναμη που να δημιουργεί ροπή συνεπώς η γωνιακή ταχύτητά του είναι σταθερή ω = 10 rad/s
διατήρηση ενέργειας Mολική g h + ½ Mολική υ2 + ½ I(O) ω2 = ½ Mολική υ'2 + ½ I(O) ω2
=> 10 2,2 + ½ 102 = ½ υ'2
=> 22 + 50 = ½ υ'2 => v'2 = 144 => v' = 12 m/s
πλάγια βολή : υ0,x = v0 συν30° = 10 3½/2 = 5 3½ m/s ,
υ0,y = v0 ημ30° = 10 0,5 = 5 m/s
x = υ0,x t = v0 συν30° t
y = h = v0 ημ30° t - ½ g t2 => - 2,2 = 10 ½ t - ½ 10 t2 => 5 t2 - 5 t - 2,2 = 0
Δ = 25 + 44 = 69 = 8,32 t = (5 ± 8,3) / 10 = 1,33 sec ή - 0,33 sec
vy = v0,y - g t = v0 ημ30° - g t = 10 ½ - 10 1,33 = 5 - 13,3 => vy = - 8,3 m/s
v2 = vx2 + vy2 = v0,x2 + vy2 = (5 3½)2 + (- 8,3)2 = 75 + 69 = 144 => v = 12 m/s
24. ΟΕΦΕ 20011 Δ
25. ΟΕΦΕ 2010
Σώμα Σ μικρών διαστάσεων με μάζα m=1kg ισορροπεί πάνω σε λείο οριζόντιο επίπεδο δεμένο στο άκρο οριζόντιου ελατηρίου σταθεράς k=100N/m και στο άκρο μη εκτατού νήματος αμελητέας μάζας. Το άλλο άκρο του οριζόντιου ελατηρίου είναι ακλόνητα στερεωμένο σε κατακόρυφο τοίχο. Ταυτόχρονα το νήμα είναι στερεωμένο στο άκρο Α ομογενούς και ισοπαχούς ράβδου ΟΑ μάζας M=0,4kg και μήκους l=0,5m. Η ράβδος μπορεί να περιστρέφεται χωρίς τριβές σε κατακόρυφο επίπεδο γύρω από σταθερό οριζόντιο άξονα που είναι κάθετος σε αυτήν και διέρχεται από το άκρο της Ο. Η ράβδος ισορροπεί σχηματίζοντας με την κατακόρυφο γωνία θ με ημθ=0,8 και συνθ=0,6 ενώ το ελατήριο στην παραπάνω θέση έχει δυναμική ενέργεια U=0,32J. 
Τη χρονική στιγμή t = 0 κόβουμε το νήμα και το σύστημα ελατήριο - σώμα Σ αρχίζει να εκτελεί απλή αρμονική ταλάντωση με σταθερά D = k ενώ η ράβδος αρχίζει να περιστρέφεται. Θεωρώντας ως δεδομένο ότι πριν κόψουμε το νήμα όλα τα σώματα της διάταξης βρίσκονται στο ίδιο κατακόρυφο επίπεδο και ότι το σώμα Σ διατηρεί συνεχώς επαφή με το οριζόντιο επίπεδο να :
(α) υπολογίσετε το μέτρο της τάσης του νήματος πριν κόψουμε το νήμα καθώς και τη δύναμη που ασκείται στη ράβδο ΟΑ στο σημείο Ο
(β) γράψετε τη σχέση απομάκρυνσης του σώματος Σ συναρτήσει του χρόνου θεωρώντας ως θετική φορά προς τα δεξιά
(γ) υπολογίσετε το μέτρο της ταχύτητας του ελεύθερου άκρου Α της ράβδου όταν διέρχεται από την κατακόρυφη θέση
(δ) βρεθεί ο ρυθμός μεταβολής της ορμής του σώματος Σ τη στιγμή που η κινητική και η δυναμική ενέργεια της ταλάντωσης θα γίνουν ίσες για πρώτη φορά
(A)
U = 0,32 J => U = ½ k Δl2 => ½ 100 Δl2 = 0,32 => Δl2 = 0,0064 => Δl = 0,08 m
ισορροπία σώματος : Τx,Σ - Fελατ = 0 => Τx,Σ - k Δl = 0 => Τx,Σ =100 0,08 m =>Τx,Σ = 8 N κατεύθυνση οριζόντια προς τα δεξιά
ισορροπία νήματος : Τx,Σ = Τx,Α = 8 N Τx,Α = 8 N κατεύθυνση οριζόντια προς τα αριστερά
Τy,Σ = Τy,Α =>
ισορροπία ράβδου :
ροπές ως προς Ο : Στ(Ο) = 0 => M g l/2 ημθ - Τx,Α l συνθ + Τy,A l ημθ = 0 => 0,4 10 /2 0,8 - 8 0,6 + Τy,A 0,8 = 0 => 1,6 - 4,8 + Τy,A 0,8 = 0 => - 3,2 + Τy,A 0,8 = 0 => Τy,A = 4 Ν κατεύθυνση κατακόρυφη προς τα κάτω
άρα Τy,Σ = 4 Ν κατεύθυνση κατακόρυφη προς τα πάνω
ΣFy = 0 => Μ g + Τy,A + Fy,O = 0 => 0,4 10 + 4 + Fy,O = 0
=> Fy,O = - 8 Ν κατεύθυνση κατακόρυφη προς τα πάνω
ΣFx = 0 => Τx,A + Fx,O = 0 => Fx,O = - 8 N κατεύθυνση οριζόντια προς τα δεξιά
ΤΣ 2 = Τx,Σ 2 + Τy,Σ 2 = 82 + 42 = 64 + 16 = 80 => ΤΣ = 80½ Ν = 4 5½ Ν
FO 2 = Fx,O 2 + Fy,O 2 = 82 + 82 = 64 + 64 = 2 64 => FO = 8 2½ Ν
(Β) , (Δ)
U = 0,32 J => U = ½ k Δl2 => ½ 100 Δl2 = 0,32 => Δl2 = 0,0064 => Δl = 0,08 m
ω2 = k / m = 100 / 1 => ω = 10 rad/s f = 10/2π = 5/π Hz T = π/5 s
x(t) = 0,08 ημ(10 t + π/2) υ(t) = 0,8 συν(10 t + π/2) α(t) = - 8 ημ(10 t + π/2) F(t) = m a(t) = - 8 ημ(10 t + π/2)
Κ = U = E/2 => x = ± Α / 2½ = ± 0,08 / 2½ = 0,08 ημ(10 t + π/2) => ημ(10 t + π/2) = ± 2½ / 2 για πρώτη φορά : ημ(10 t + π/2) = 2½ / 2
dp/dt = F(t) = m a(t) = - 8 ημ(10 t + π/2) = - 8 2½ / 2 = - 4 2½ N
(Γ)
h = l/2 - l/2 συνθ = 0,25 ( 1 - 0,6 ) = 0,1 m
M g h = ½ Ι(Ο) ω2 => M g h = ½ 1/3 M l2 ω2 => 0,4 10 0,1 = ½ 1/3 0,4 0,52 ω2 => 1 = 1/6 1/4 ω2 => ω2 = 24 => ω = 2 6½ rad/s
υΑ = ω l = 2 6½ 0,5 = 6½ m/s

26. ΟΕΦΕ 2009
Ο δίσκος τροχαλίας είναι ομογενής έχει μάζα Μ = 2 kg ακτίνα R = 0,2 m και ροπή αδράνειας ως προς τον άξονα περιστροφής που περνάει από το κέντρο του Κ και είναι κάθετος στο επίπεδό του Ι(Κ) = ½ Μ R2. Ο άξονας περιστροφής Κ είναι το άκρο αβαρούς ράβδου ΚΑ της οποίας το άλλο άκρο Α είναι στερεωμένο με αρθρωση στην οροφή. Το σύστημα ράβδος - τροχαλία μπορεί να στραφεί περί την άρθρωση Α στο ίδιο κατακόρυφο επίπεδο του δίσκου της τροχαλίας. Τριβές στον άξονα περιστροφής και στην άρθρωση δεν υπάρχουν.
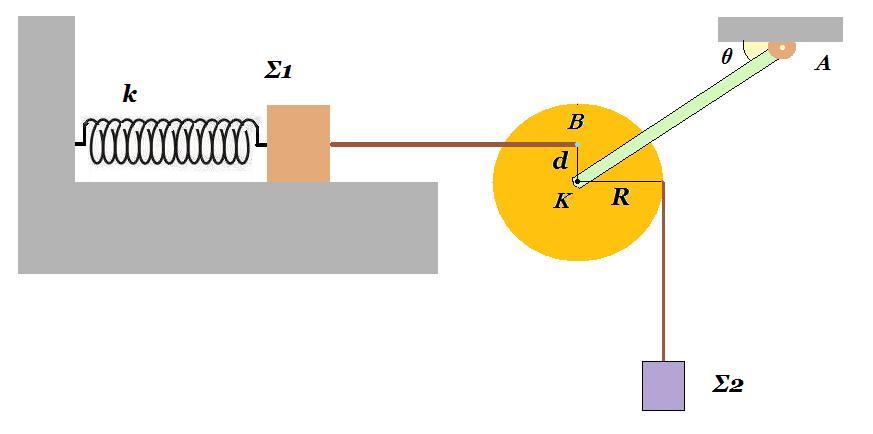
Σώμα Σ1 μάζας m1 = 4 kg είναι προσδεμένο στο ελεύθερο άκρο ιδανικού ελατηρίου σταθεράς k = 100 N/m το άλλο άκρο του οποίου είναι στερεωμένοσε ακλόνητο σημείο. Το σύστημα [ σώμα Σ1 - ελατήριο ] είναι πάνω σε λείο οριζόντιο επίπεδο και στο ίδιο κατακόρυφο επίπεδο που βρίσκεται ο δίσκος της τροχαλίας. Η διάταξη είναι σεισορροπία. Το νήμα που είναι δεμένο το σώμα Σ1 με τον δίσκο της τροχαλίας είναι οριζόντιο. Το σημείο πρόσδεσης Β στον δίσκο της τροχαλίας είναι στην ίδια κατακόρυφο με το Κ και σε απόσταση ΚΒ = d = 0,1 m ενώ η ράβδος ΑΚ σχηματίζει γωνία θ με την οριζόντια οροφή. Το σώμα Σ2 μάζας m2 = 2 kg είναι δεμένο σε νήμα το οποίο έχει τυλιχθεί αρκετές φορές στο αυλάκι του δίσκου της τροχαλίας. Τα νήματα θεωρούνται αβαρή λεπτά και μη εκτατά.
Α. Υπολογίστε το μέτρο της δύναμης που ασκεί η αβαρής ράβδος ΑΚ στον άξονα Κ της τροχαλίας.
Προσδιορίστε την γωνία θ.
Συγκολλούμε την άρθρωση Α ώστε η αβαρής ράβδος να παραμένει ακλόνητη στη θέση που προσδιορίστηκε προηγουμένως και τη στιγμή t = 0 κόβουμε το οριζόντιο νήμα. Τότε το σώμα Σ1 εκτελεί απλή αρμόνική ταλάντωση με D = k και θετική φορά προς τα δεξιά ενώ το σώμα Σ2 κινείται προς τα κάτω. Το κατακόρυφο νήμα στο οποίο είναι δεμένο ξετυλίγεται χωρίς να ολισθαίνει στο αυλάκι του δίσκου της τροχαλίας μένοντας κατακόρυφο.
B. Γράψτε την εξίσωση της απομάκρυνσης της ταλάντωσης του σώματος Σ1 υναρτήσει του χρόνου.
Γ. Τη στιγμή που το σώμα Σ1 περνά από τη θέση ισορροπίας του για δεύτερη φορά να υπολογίσετε τον ρυθμό μεταβολής της κινητικής ενέργειας του σώματος Σ2 και την στροφορμή του δίσκου της τροχαλίας.
A.
ισορροπία Σ1 : Fελατ = Τ1 => k Δl = Τ1
ισορροπία Σ2 : m2 g = Τ2 => 2 10 = Τ2 = 20 N
ισορροπία τροχαλίας :
ροπές ως προς Κ : Στ(Κ) = 0 => Τ2 R = T1 d => Τ2 0,2 = T1 0,1 => 2 Τ2 = T1 => Τ1 = 40 N
τότε Δl = Τ1 / k = 40 / 100 => Δl = 0,4 m
ΣFx = 0 => T1 = Fx,K => Fx,K = 40 N
ΣFy = 0 => Μ g + T2 = Fy,K => Fy,K = 2 10 + 20 = 40 N
FK 2 = Fx,K 2 + Fy,K 2 = 40 2 + 40 2 => FK = 40 2½ Ν
ισορροπία ράβδου ΑΚ :
ΣFx = 0 => Fx,K = Fx,A => Fx,A = 40 N
ΣFy = 0 => Fy,K = Fy,A => Fy,A = 40 N
FK 2 = Fx,K 2 + Fy,K 2 = 40 2 + 40 2 => FK = 40 2½ Ν
εφθ = Fy,A / Fx,A = 40 / 40 =1 => θ = 45°
Β.
ω2 = k / m1 = 100 / 4 = 25 => ω = 5 rad/s T = 2π/ω = 2π/5 s
x(t) = 0,4 ημ(5 t + π/2) v(t) = 2 συν(5 t + π/2) α(t) = - 10 ημ(5 t + π/2)
F(t) = m1 a = - 40 ημ(5 t + π/2)
ΣF = m1 a => Fελατ (t) = - 40 ημ(5 t + π/2) Fελατ (0) = - 40 ημ(π/2) = - 40 N
Γ.
t = 3T/4 = 3/4 2π/5 = 3π/10 s
T R = I(K) aγων => T R = ½ Μ R2 aγων => T = ½ Μ R aγων = ½ Μ α (1)
m2 g - T = m2 a (2)
(1) , (2) => m2 g - ½ Μ α = m2 a => m2 g = ½ Μ α + m2 a => m2 g / ( ½ Μ + m2 ) = a
=> α = 2 10 / ( ½ 2 + 2 ) => a = 20/3 m/s2
αγων = α / R = 20/3 / 0,2 = 100/3 rad/s2
dK/dt = m2 a v = m2 a a t = 2 20/3 20/3 3π/10 = 80π/3 J/s
L = I(K) ω = ½ Μ R2 aγων t = ½ 2 0,22 100/3 3π/10 = 0,04 10π = 0,4 π kg m2 /s
27. Συµπαγής οµογενής σφαίρα µάζας m = 10 kg και ακτίνας R = 0,1 m κυλίεται ευθύγραµµα χωρίς ολίσθηση ανερχόµενη κατά µήκος κεκλιµένου επιπέδου γωνίας φ µε ηµφ = 0,56. Τη χρονική στιγµή t=0 το κέντρο µάζας της σφαίρας έχει ταχύτητα µε µέτρο υ0 = 8 m/s. Να υπολογίσετε για τη σφαίρα:
α. το µέτρο της γωνιακής ταχύτητας περιστροφής της τη χρονική στιγµή t=0.
β. το µέτρο της επιτάχυνσης του κέντρου µάζας της.
γ. το µέτρο του ρυθµού µεταβολής της στροφορµής κατά τη διάρκεια της κίνησής της.
δ. το µέτρο της ταχύτητας του κέντρου µάζας της καθώς ανεβαίνει, τη στιγµή που έχει διαγράψει 30/π περιστροφές.
∆ίνονται η ροπή αδράνειας της σφαίρας περί άξονα διερχόµενο από το κέντρο της Ι = 2/5 m R2 και η επιτάχυνση της βαρύτητας: g = 10 m/s2.
(α) υ0 = ω0 R => ω0 = υ0 / R = 8 / 0,1 => ω0 = 80 rad/s
(β) T R = I aγων => T R = 2/5 m R2 aγων => T = 2/5 m R aγων = 2/5 m a
- T - m g ημφ = m a => - 2/5 m a - m g ημφ = m a => - 2/5 a - a = g ημφ =>
=> - 7/5 a = g ημφ => a = - 5/7 10 0,56 => α = - 4 m/s2
τότε aγων = α / R = 4 / 0,1 => aγων = 40 rad/s2
και T = 2/5 m a = 2/5 10 4 => Τ = 16 Ν
(γ) dL/dt = Στ(Ο) = T R = 2/5 m R2 aγων = 2/5 10 0,01 40 => dL/dt = 8/5 Nm
(δ) Ν = 30/π περιστροφές θ = 2π Ν = 2π 30/π => θ = 60 rad
θ = ω0 t - ½ aγων t2 => 60 = 80 t - ½ 40 t2 => t2 - 4 t + 3 = 0 => t = 1 s , t = 3 s
t = 1 s τότε θ = ω0 t - ½ aγων t2 = 80 1 - ½ 40 12 = 60 rad το σώμα ανέρχεται
και ω = ω0 - aγων t = 80 - 40 1 => ω = 40 rad/s υ = υ0 - α t = 8 - 4 1 => υ = 4 m/s
t = 3 s τότε θ = ω0 t - ½ aγων t2 = 80 3 - ½ 40 32 = 240 - 180 = 60 rad το σώμα κατέρχεται
και ω = ω0 - aγων t = 80 - 40 3 => ω = - 40 rad/s υ = υ0 - α t = 8 - 4 3 => υ = - 4 m/s 
28. H διπλή τροχαλία του σχήματος αποτελείται από δύο ομοαξονικούς κυλίνδρους (1) και (2) που έχουν μάζες Μ1 = 2 kg και Μ2 = 4 kg και ακτίνες R1 = 2 m και R2 = 1 m αντίστοιχα. Η τροχαλία μπορεί να περιστρέφεται γύρω από ακλόνητοοριζόντιο άξονα χ'χ που ταυτίζεται με τον άξονα συμμετρίας των δύο κυλίνδρων. Στην περιφέρεια του κυλίνδρου (1) έχουμε τυλίξει πολλές φορές ένα αβαρές και μη εκτατό νήμα, στο ελεύθερο άκρο του οποίου έχουμε δέσει σώμα Σ1 μάζας m1 = 2 kg. Γύρω από τον κύλινδρο (2) έχουμε τυλίξει άλλο αβαρές και μη εκτατό νήμα , στο ελεύθερο άκρο του οποίου έχουμε δέσει σώμα Σ2 μάζας m2. Η ράβδος ΑΓ μάζας Μ = 2 kg, μήκους L = 1,2 m ισορροπεί οριζόντια. Το ένα άκρο Α της ράβδου συνδέεται με άρθρωση σε κατακόρυφο τοίχο, ενώ το άλλο άκρο της Γ συνδέεται με το σώμα Σ1 μέσω αβαρούς κατακόρυφου νήματος.
Δ1. Υπολογίστε τις δυνάμεις που δέχεται η ράβδος στα άκρα της Α και Γ.
Δ2. Υπολογίστε τη δύναμη που ασκείται στο κέντρο Κ της τροχαλίας και δείξτε ότι η μάζα του σώματος Σ2 είναι m2 = 6 kg.
Στο άκρο Γ της ράβδου στερεώνουμε πολύ μικρό σώμα μάζας m = 1 kg και τη στιγμή t = 0 κόβουμε το νήμα που συνδέει τη ράβδο με το σώμα Σ1 οπότε η ράβδος αρχίζει να περιστρέφεται χωρίς τριβές γύρω από την άρθρωσή της Α και η διπλή τροχαλία αρχίζει να περιστρέφεται χωρίς τριβές γύρω από τον άξονα χ'χ.
Δ3. Υπολογίστε το μέτρο της γωνιακής επιτάχυνσης της τροχαλίας.
Δ4. Υπολογίστε την ολική κινητική ενέργεια του συστήματος < τροχαλίας - σώμα Σ1 - σώμα Σ2 > τη στιγμή t = 2 s και πόσο απέχουν τα σώματα Σ1 - Σ2 εκείνη τη στιγμή;
Δ5. Υπολογίστε την γωνιακή επιτάχυνση του συστήματος << ράβδος - μάζα m >> τη στιγμή t = 0 καθώς και την στρoφορμή της ράβδου ως προς τον άξονα περιστροφής της την στιγμή κατά την οποία σχηματίζει γωνία 30° με την οριζόντιο.
Δ1. ροπές ως προς Α : M g L/2 = TΓ L => 2 10 0,6 = TΓ 1,2 => TΓ = 10 Ν
ροπές ως προς Γ : M g L/2 = FΑ L => 2 10 0,6 = FΑ 1,2 => FΑ = 10 Ν
Δ2. ισορροπία Σ1 : ΤΓ + m1 g = T1 => T1 = 10 + 2 10 => T1 = 30 N
ισορροπία τροχαλίας : ροπές ως προς Κ : T1 R1 = T2 R2 => T2 1 = 30 2 => T2 = 60 N
ΣFy = 0 => FK - Mτροχ g - T1 - T2 = 0 => FK = (2+4) 10 + 30 + 60 => FK = 150 N
ισορροπία Σ2 : m2 g = T2 => m2 10 = 60 => m2 = 6 kg
Δ3. α2 = αγων R2 = αγων α1 = αγων R1 = αγων 2 => α1 = 2 α2 = 2 αγων
m2 g - T2 = m2 α2 => 60 - T2 = 6 αγων (1)
I(K) = ½ Μ1 R12 + ½ Μ2 R22 = ½ 2 22 + ½ 4 12 = 4 + 2 = 6 kg m2
T2 R2 - T1 R1 = I(K) αγων => T2 1 - T1 2 = 6 αγων => T2 - 2 T1 = 6 αγων (2)
T1 - m1 g = m1 α1 => T1 - 20 = 2 αγων 2 => 2 T1 - 40 = 8 αγων (3)
(1) + (2) + (3) => 60 - 40 = 20 αγων => αγων = 1 rad/s2 α1 = 2 m/s2 α2 = 1 m/s2
Δ4. υ1 = α1 t = 2 m/s2 2 s = 4 m/s υ2 = α2 t = 1 m/s2 2 s = 2 m/s ω = αγων t = 1 2 = 2 rad/s
Kολ = ½ m1 v12 + ½ m2 v22 + ½ I(K) ω2 = ½ 2 42 + ½ 6 22 + ½ 6 22 = 16 + 12 + 12 = 40 J
h1 = ½ α1 t2 = ½ 2 22 = 4 m ανέρχεται h2 = ½ α2 t2 = ½ 1 22 = 2 m κατέρχεται
Δh = 4 m + 2 m = 6 m κατακόρυφη απόσταση σωμάτων Σ1 και Σ2 όταν t = 2 s
Δ5. Στ(Α) = Ι αγων => M g L/2 + m g L = ( 1/3 M L2 + m L2 ) αγων =>
=> 2 10 0,6 + 1 10 1,2 = ( 1/3 2 1,22 + 1 1,22 ) αγων =>
=> 12 + 12 = ( 0,96 + 1,44 ) αγων => 24 = 2,4 ω => αγων = 10 rad/s2 αρχική γωνιακή επιτάχυνση
διατήρηση ενέργειας : M g L/2 ημ30° + m g L ημ30° = ½ ( 1/3 M L2 + m L2 ) ω2
=> 2 10 0,6 ½ + 1 10 1,2 ½ = ½ 2,4 ω2 => 6 + 6 = 1,2 ω2 => ω2 = 10 => ω = 10½ rad/s
Lράβδου = Ιρ ω = 0,96 10½ kg m2/s
29. Tο στερεό αποτελείται από δύο όμοιους δίσκους μάζας Μ1 = 1 kg και ακτίνας R1 = 0,4 m ο καθένας και εσωτερικό κύλινδρο μάζας Μ2 = 2 kg και ακτίνας R2 = 0,2 m. Υπολογίστε την ροπή αδράνειας του στερεού ως προς τον άξονα χ'χ που συμπίπτει με τον άξονα συμμετρίας του κυλίνδρου και διέρχεται από τα κέντρα Κ και Κ' των δύο δίσκων.
Στερεώνουμε το στερεό σώμα ώστε να μπορεί να περιστρέφεται χωρίς τριβές γύρω από τον άξονα χ'χ. Γύρω από τον κύλινδρο στην περιφέρειά του τυλίγουμε πολλές φορές αβαρές νήμα μη εκτατό και στο ελεύθερο άκρο του δένουμε σώμα Σ μάζας m = 5 kg. Αρχικά το σύστημα είναι ακίνητο και το νήμα τεντωμένο. Τη χρονική στιγμή t = 0 αφήνουμε το σύστημα ελεύθερο να κινηθεί οπότε το στερεό περιστρέφεται περί τον άξονα χ'χ και το σώμα Σ κινείται κατακόρυφα προς τα κάτω. Το νήμα δεν ολισθαίνει στην περιφέρεια του κυλίνδρου.
Δ1. Υπολογίστε την επιτάχυνση με την οποία κινείται το σώμα Σ.
Δ2. Υπολογίστε την στροφορμή του συστήματος << στερεό σώμα - σώμα Σ >> ως προς τον άξονα χ'χ την στιγμή που το στερεό έχει εκτελέσει κατά Ν = 25/π περιστροφές.
Τοποθετούμε το σύστημα των σωμάτων πάνω σε δύο οριζόντιες σανίδες ώστε οι δύο δίσκοι του στερεού να βρίσκονται συνεχώς σε επαφή με τις σανίδες και το σώμα Σ κρέμεται δεμένο στο νήμα. Αρχικά το σύστημα είναι ακίνητο και το νήμα τεντωμένο. Τη χρονική στιγμή t = 0 αφήνουμε το σύστημα ελεύθερο να κινηθεί οπότε οι δίσκοι του στερεού κυλίονται χωρίς να ολισθαίνουν πάνω στις σανίδες και το σώμα Σ κινείται κατακόρυφα προς τα κάτω. Το νήμα δεν ολισθαίνει στην περιφέρεια του κυλίνδρου.
Δ3. Υπολογίστε την γωνιακή επιτάχυνση του στερεού.
Δ4. Υπολογίστε την γωνιακή ταχύτητα του στερεού τη στιγμή που το σώμα Σ έχει μετατοπισθεί κατακόρυφα Η = 162,5 m.
Ι = 2 ½ Μ1 R12 + ½ Μ2 R22 = 2 ½ 1 0,42 + ½ 2 0,22 = 0,16 + 0,04 = 0,2 kg m2
Δ1.
Στ(χ'χ) = Ι αγων => Τ R2 = I αγων => Τ = I αγων /R2 αγων = a / R2
mg - T = ma => mg - I αγων / R2 = m αγων R2 => 50 = 0,2 αγων / 0,2 + 5 αγων 0,2 =>
=> 50 = αγων + αγων => αγων = 25 rad/s2 a = 25 0,2 = 5 m/s2
Δ2.
θ = ½ αγων t2 => 2πΝ = ½ αγων t2 => 2π 25/π = ½ 25 t2 => t = 2 sec ω = αγων t = 50 rad/s
L = ( I + m R2 2 ) ω = ( 0,2 + 5 0,22 ) 50 = 0,4 50 => L = 20 kg m2/s
Δ3.
vcm = ω R1 => acm = αγων R1
ΣF = ( 2 M1 + M2 ) acm => Α = ( 2 M1 + M2 ) acm => Α = ( 2 1 + 2 ) acm = 4 acm = 1,6 αγων
Στ(χ'χ) = Ι αγων => Τ R2 - Α R1 = I αγων => Τ 0,2 - 1,6 αγων 0,4 = 0,2 αγων =>
=> Τ - 3,2 aγων = αγων => Τ = 4,2 αγων
mg - T = ma => mg - 4,2 αγων = m αγων R2 => 50 = 4,2 αγων + 5 αγων 0,2 =>
=> 50 = 5,2 αγων => αγων = 50/5,2 = 125/13 rad/s2
a = 125/13 0,2 = 25/13 m/s2 acm = 125/13 0,4 = 50/13 m/s2
Δ4.
H = ½ α t2 => 162,5 = ½ 25/13 t2 => t = 13 sec
ω = αγων t = 125/13 13 => ω = 125 rad/s
Κπεριστροφ + Κμεταφορ + Κ(Σ) =
= ½ 0,2 1252 + ½ 4 502 + ½ 5 252 = 1.562,5 J + 5.000 J + 1.562,5 J =
= 6.562,5 J + 1.562,5 J = 8.125 J = 5kg 10m/s2 162,5m = m g H
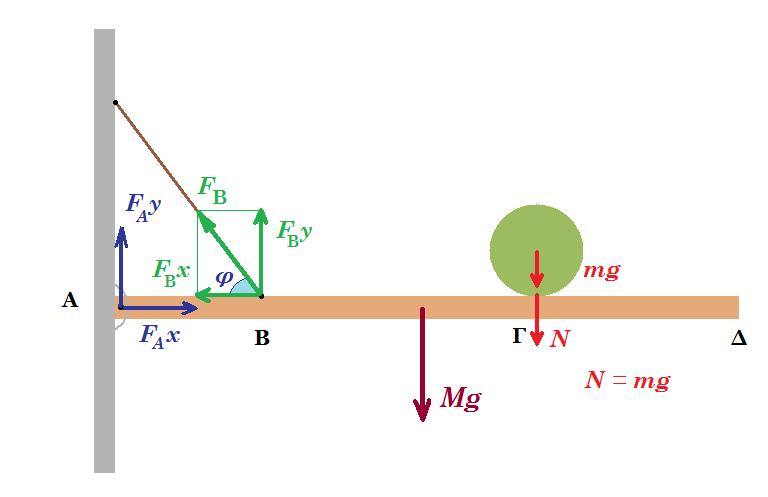
30. Λεπτή ομογενής ράβδου ΑΔ έχει μήκος L=6m και μάζα Μ=4Κg. Η ράβδος είναι αρθρωμένη στο άκρο της Α και ηρεμεί σε οριζόντια θέση με τη βοήθεια αβαρούς μη εκτατού νήματος που το ένα άκρο του είναι προσδεμένο στο σημείο Β της ράβδου, ενώ το άλλο του άκρο στερεωμένο στον κατακόρυφο τοίχο. Το νήμα σχηματίζει γωνία φ με τη ράβδο (ημφ=0,8 και συνφ=0,6) ενώ η απόσταση (ΑΒ)=L/4.
Στο σημείο Γ της ράβδου ισορροπεί ομογενής σφαίρα μάζας m=3Kg και ακτίνας r=0,1m ενώ η απόσταση του κέντρου μάζας της από το άκρο Δ της ράβδου είναι (ΓΔ)=L/3.
Δ1. Να υπολογίσετε το μέτρο της δύναμης που ασκείται στη ράβδο από την άρθρωση.
Τη χρονική στιγμή t=0 ασκείται στο ανώτερο σημείο της σφαίρας σταθερή οριζόντια δύναμη μέτρου F=2,1N, με φορά προς τα δεξιά. Η σφαίρα αρχίζει να κυλίεται χωρίς να ολισθαίνει πάνω στη ράβδο.
Δ2. Να υπολογίσετε το μέτρο της γωνιακής επιτάχυνσης της σφαίρας.
Η ροπή αδράνειας της σφαίρας ως προς άξονα που διέρχεται από το κέντρο μάζας της υπολογίζεται από τη σχέση: I = 2/5 m r2
Δ3. Να υπολογίσετε το μέτρο της γωνιακής ταχύτητας της σφαίρας τη στιγμή t1 κατά την οποία εγκαταλείπει τη ράβδο.
Δ4. Να υπολογίσετε τον αριθμό των περιστροφών που εκτελεί η σφαίρα σε χρονικό διάστημα Δt=1s από τη στιγμή που εγκατέλειψε τη ράβδο , καθώς και την ταχύτητα που έχει αποκτήσει το κέντρο μάζας της σε αυτό το χρονικό διάστημα.
Δίνεται η επιτάχυνση της βαρύτητας g=10m/s2.
ροπές ως προς Α : Μg L/2 + mg 2L/3 - FBy L/4 = 0 => 40 3 + 30 4 = FBy 1,5 =>
=> FBy = 160 N
FBx = FBy / εφφ => FBx = 160 N / (4/3) = 120 N
FAx = FBx = 120 N
ΣFy = 0 => FAy + FBy = Mg + N => FAy + 160 = 40 + 30 => FAy = - 90 N κατακόρυφη προς τα κάτω
FA2 = FAx2 + FAy2 => FA2 = 1202 + 902 = 14400 + 8100 = 22500 => FA = 150 N
έστω η τριβή αντίρροπη της F : ΣF = m a => F - T = m α (1)
Στ(Κ) = Ι αγων => ( F + T ) r = 2/5 m r2 αγων => F + T = 2/5 m r αγων =>
=> F + T = 2/5 m α (2)
(1) + (2) => 2 F = 7/5 m a => a = 10F / 7m = 21/21 = 1 m/s2 αγων = a / r = 10 rad/s2
(2) - (1) => 2 T = - 3/5 m a => T = - 3/10 m a T , F ομόρροπες
x = ½ a t2 => L/3 = 6/3 = ½ 1 t2 => t2 = 4 => t = 2 s v0 = a t = 1 2 = 2 m/s
ω = αγων t = 10 2 = 20 rad/s
η γωνιακή ταχύτητα της σφαίρας παραμένει σταθερή διότι η μόνη δύναμη που ασκείται σ'αυτήν είναι το βάρος της που η ροπή της ως προς το κέντρο της είναι μηδέν έτσι θ = ω t = 20 1 = 20 rad και Ν = 20 / 2π = 10 / π περιστροφές
υ2 = υ0 2 + (g t) 2 = 22 + 102 = 104 => v = 104½ m/s
M g h + ½ M υ2 + ½ I(Κ) ω2 = ½ M υ'2 + ½ I(Κ) ω2
3 10 h + ½ 3 22 = ½ 3 104 => 20 h = 104 - 4 = 100 => h = 5 m = ½ 10 12 = ½ g t2
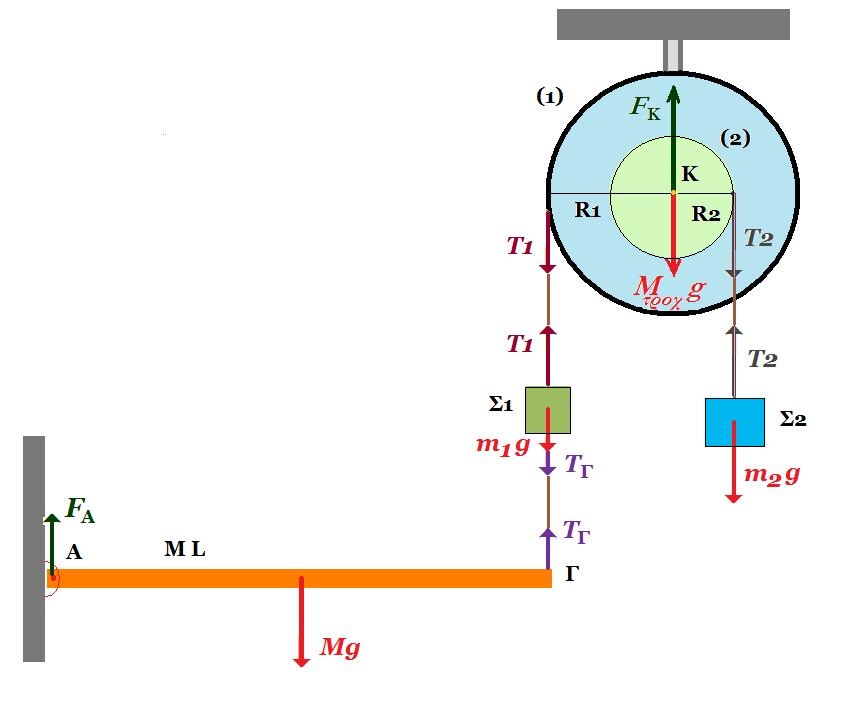
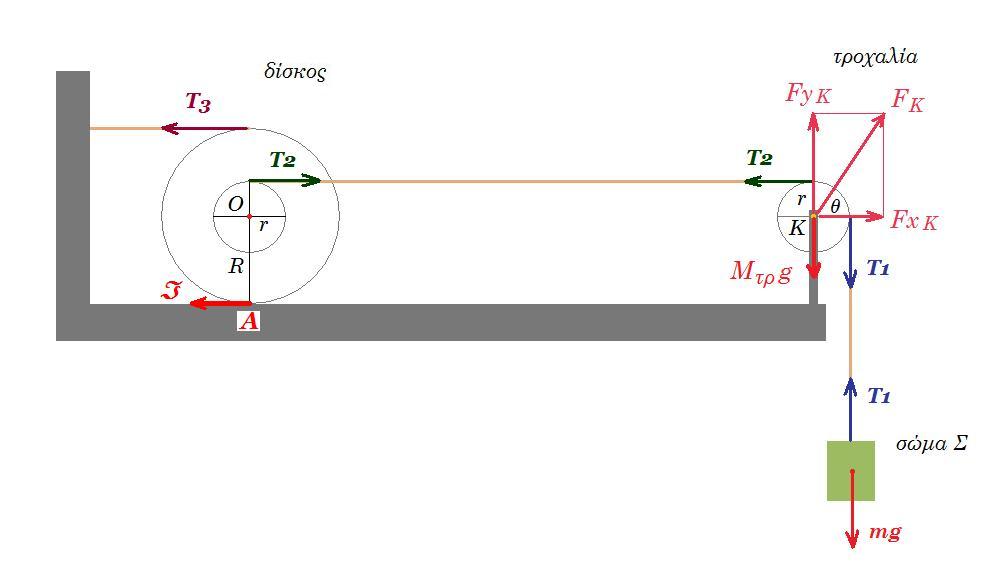
31. Η διπλή τροχαλία αποτελείται από δύο ομογενείς δίσκους με ακτίνες r και R = 1 m αντίστοιχα, που συγκολούνται μεταξύ τους έχοντας κοινό κέντρο Ο. Η διπλή τροχαλία μπορεί να περιστρέφεται χωρίς τριβές γύρω από ακλόνητο οριζόντιο άξονα που διέρχεται από το κοινό κέντρο των δύο δίσκων και είναι κάθετος στο επίπεδο τους. Η ροπή αδράνειας της τροχαλίας ως προς τον άξονα περιστροφής της είναι Ιτρ = 0,5 kg m2. Στην περιφέρεια του δίσκου (Ι) έχουμε τυλίξει πολλές φορές αβαρές και μη εκτατό νήμα, στο ελεύθερο άκρο του οποίου ασκούμε σταθερή οριζόντια δύναμη F = 10 N. Στην περιφέρεια του δίσκου (ΙΙ) έχουμε τυλίξει πολλές φορές δεύτερο αβαρές και μη εκτατό νήμα, που είναι επίσης τυλιγμένο πολλές φορές στην περιφέρεια κατακόρυφου δίσκου (ΙΙΙ) μάζας Μ = 4 kg και ακτίνας R = 1 m. Το κέντρο Κ του δίσκου (ΙΙΙ) συνδέεται μέσω άλλου αβαρούς και μη εκτατού νήματος με σώμα Σ, μάζας m = 1 kg που είναι στερεωμένο μόνιμα στο ελεύθερο άκρο ιδανικού οριζόντιου ελατηρίου σταθεράς k = 100 N/m. Το άλλο άκρο του ελατηρίου είναι στερεωμένο σε ακλόνητο σημείο κατακόρυφου τοιχώματος. Το σύστημα διπλή τροχαλία - δίσκος (ΙΙΙ) - σώμα Σ - ελατήριο - νήματα ισσρροπεί ακίνητο με το ελατήριο επιμηκυμένο έχοντας δυναμική ενέργεια Uελ = 0,5 J.
Δ1. Υπολογίστε το μέτρο της στατικής τριβής που ασκείται στον δίσκο (ΙΙΙ) από το τμήμα 1 του οριζόντιου δαπέδου και την ακτίνα του δίσκου (Ι) της διπλής τροχαλίας.
Τη χρονική στιγμή t0 = 0 κόβουμε το νήμα που συνδέει τον δίσκο (ΙΙΙ) με το σώμα Σ οπότε ο μεν δίσκος αρχίζει να κυλίεται χωρίς να ολισθένει επάνω στο τμήμα 1 του οριζόντιου δαπέδου και το σώμα Σ αρχίζει να εκτελεί Α.Α.Τ. επάνω στο λείο τμήμα 2 του οριζόντιου δαπέδου.
Δ2. Βρείτε ποιές χρονικές στιγμές η επιτάχυνση του σώματος Σ ισούται με το ήμισυ της μέγιστης τιμής της. Ποιά είναι η θέση του σώματος Σ όταν συμβαίνει για πρώτη φορά;
Δ3. Υπολογίστε το μέτρο της επιτάχυνσης acm του κέντρου μάζας του δίσκου (ΙΙΙ).
Τη χρονική στιγμή t3 το μέτρο της γωνιακής ταχύτητας περιστροφής της διπλής τροχαλίας είναι ωτρ = 1 rad/s.
Δ4. Υπολογίστε την κινητική ενέργεια του δίσκου (ΙΙΙ) και την κινητική ενέργεια της τροχαλίας τη στιγμή t3, καθώς και το ποσοστό του έργου που παράγει η δύναμη F από τη στιγμή t0 = 0 έως τη στιγμή t3.
(Δ1) F r = T1 R (1)
T1 R = Ts R => T1 = Ts (2)
T2 = T1 + Ts (3)
Uελατ = ½ k x02 => 0,5 = ½ 100 x02 => x02 = 0,01 => x0 = 0,1 m
Fελατ = k x0 = 100 0,1 = 10 N (4)
Fελατ = T2 = 10 N (5)
(2), (3), (5) => T1 = Ts = 5 N (6)
(1) , (6) => F r = T1 R => 10 r = 5 1 => r = 0,5 m
(Δ2) το ελατήριο αρχικά είναι επιμηκυμένο κατά 0,1 m που είναι το πλάτος της ταλάντωσης του σώματος ω2 = k / m 100 / 1 => ω = 10 rad/s x(t) = 0,1 ημ(10t + 3π/2)
v(t) = 1 συν(10t + 3π/2) α(t) = - 10 ημ(10t + 3π/2) ΣF(t) = m a(t) = - 10 ημ(10t + 3π/2)
ημ(10t + 3π/2) = ± ½ = ημπ/6 ή ημ5π/6 ή ημ7π/6 ή ημ11π/6
10t + 3π/2 = 2Νπ + π/6 => 10t = 2Νπ + π/6 - 3π/2 => 10t = 2Νπ - 4π/3 Ν = 1,2,3, ... Ν = 1 : t = π/15 s
x(π/15) = 0,1 ημ(10 π/15 + 3π/2) = 0,1 ημ(2π/3 + 3π/2) = 0,1 ημ(13π/6) = 0,1 (+½) = + 0,05 m
ή 10t + 3π/2 = 2Νπ + 5π/6 => 10t = 2Νπ + 5π/6 - 3π/2 => 10t = 2Νπ - 2π/3 Ν = 1,2,3, ...
Ν = 1 : t = 2π/15 s
x(2π/15) = 0,1 ημ(10 2π/15 + 3π/2) = 0,1 ημ(4π/3 + 3π/2) = 0,1 ημ(17π/6) = 0,1 (+½) = + 0,05 m
ή 10t + 3π/2 = 2Νπ + 7π/6 => 10t = 2Νπ + 7π/6 - 3π/2 => 10t = 2Νπ - π/3 Ν = 1,2,3, ...
Ν = 1 : t = π/6 s
x(π/6) = 0,1 ημ(10 π/6 + 3π/2) = 0,1 ημ(5π/3 + 3π/2) = 0,1 ημ(19π/6) = 0,1 (-½) = - 0,05 m
ή 10t + 3π/2 = 2Νπ + 11π/6 => 10t = 2Νπ + 11π/6 - 3π/2 => 10t = 2Νπ + π/3 Ν = 0,1,2, ...
Ν = 0 : t = π/30 s
x(π/30) = 0,1 ημ(10 π/30 + 3π/2) = 0,1 ημ(π/3 + 3π/2) = 0,1 ημ(11π/6) = 0,1 (-½) = - 0,05 m
(Δ3) v(Θ) = v(Μ) = vcm + ωδ R = 2 vcm => α(Θ) = α(Μ) = aγων,δ R + αcm = 2 αcm =>
=> aγων,τρ R = 2 aγων,δ R = 2 αcm
T1 + Ts = M acm (7)
T1 R - Ts R = Iδ aγων,δ => T1 R - Ts R = ½ Μ R2 aγων,δ => T1 - Ts = ½ Μ R aγων,δ => T1 - Ts = ½ Μ acm (8)
(7) + (8) => 2 Τ1 = 3/2 Μ acm (9)
F r - T1 R = Iτρ aγων,τρ => 10 0,5 - T1 1 = 0,5 aγων,τρ => 10 - 2T1 = aγων,τρ = 2 αcm (10)
(9) + (10) => 10 = (3/2 4 + 2) αcm => 10 / (6 + 2) = αcm = 5/4 m/s2
aγων,τρ R = 2 aγων,δ R = 2 αcm => aγων,τρ = 5/2 rad/s2 & aγων,δ = 5/4 rad/s2
vN = ωτρ r vΘ = ωτρ R
vΘ = vM = 2 vcm => ωτρ R = vM = 2 vcm => 1 rad/s 1 m = 2 vcm => vcm = 0,5 m/s
vN = vΘ r / R = 2 vcm r / R = 2 0,5m/s 0,5m / 1m = 0,5 m/s
ωτρ = αγων,τρ t => 1 rad/s = 5/2 rad/s2 t => t = 0,4 s
ωδ = αγων,δ t = 5/4 rad/s2 0,4 s = 0,5 rad/s
Kδ = ½ Ιδ ωδ2 + ½ Μ υcm2 = ½ ½ Μ R2 ωδ2 + ½ Μ υcm2 = ½ ½ Μ υcm2 + ½ Μ υcm2 = 3/4 Μ υcm2 = 3/4 4 0,52 => Κδ = 3/4 J
WF = F s = F r θ = τ θ = F r ½ αγων,τρ t2 = 10 0,5 ½ 5/2 0,42 => WF = 1 J
Kδ / WF = 3/4 => 75%
Kτρ = ½ Ιτρ ωτρ2 = ½ 0,5 12 => Κτρ = 1/4 J
συμπέρασμα : WF = Kδ + Kτρ
32. Η διάταξη του σχήματος είναι σε ισορροπία. Δείξτε ότι ο δίσκος δέχεται δύναμη στατικής τριβής μέτρου 10 Ν και υπολογίστε την δύναμη που ασκείται στην τροχαλία στο κέντρο της Κ.
Την χρονική στιγμή t0 = 0 κόβουμε το νήμα που συνδέει τον δίσκο με το τοίχωμα, οπότε ο δίσκος κυλίεται χωρίς να ολισθαίνει, η τροχαλία στρέφεται περί το κέντρο της Κ και το σώμα Σ κινείται κατακόρυφα προς τα κάτω με επιτάχυνση α. Υπολογίστε την γωνιακή επιτάχυνση του δίσκου.
Αν το σώμα Σ κατέρχεται διανύοντας απόσταση y = 24 m πόση είναι η διανυόμενη απόσταση xcm του κέντρου μάζας του δίσκου; Πόση είναι η κινητική ενέργεια και ο ρυθμός μεταβολής της κινητικής ενέργειας του δίσκου εκείνη την χρονική στιγμή;
r = 0,4 m, R = 0,8 m, m = 4 kg, Μτρ = 8 kg, Μδ = 8 kg

ισορροπία σώματος Σ : Τ1 = m g = 4 kg 10 m/s2 => T1 = 40 N
τροχαλία Στ(Κ) = 0 => Τ1 r = T2 r => T2 = T1 = 40 N
δίσκος Στ(Α) = 0 => Τ2 (R + r) = T3 2R => 40N (0,8m + 0,4m) = T3 2 0,8m => T3 = 30 N
ΣFx = 0 => T2 - T3 - Α = 0 => Α = T2 - T3 = 40N - 30N => Α = 10 N
τροχαλία ΣFx = 0 => FxK - T2 = 0 => FxK = T2 = 40 N
ΣFy = 0 => FyK - Mτρ g - T1 = 0 => FyK = 8 10 + 40 => FyK = 120 N
εφθ = FyK / FxK = 120N / 40Ν => εφθ = 3
FK 2 = FxK2 + FyK2 = 402 + 1202 = 10 402 => FK = 40 Φ10 N
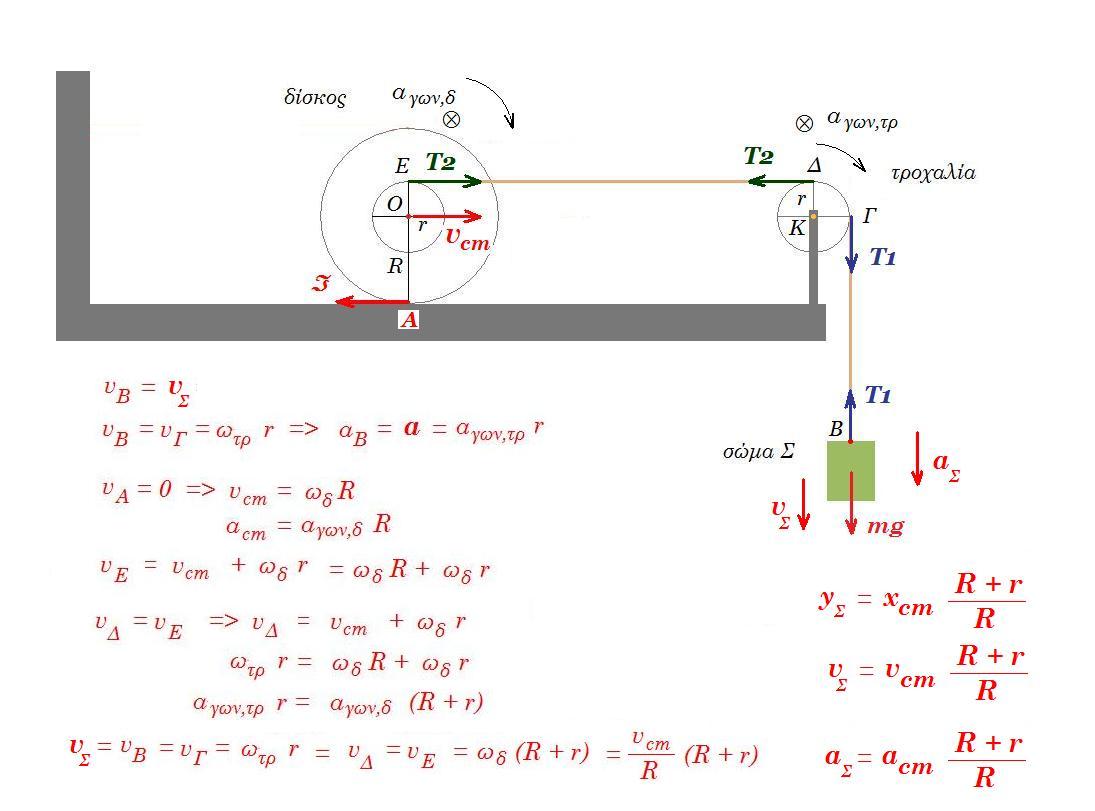
α = r αγων,τρ
αγων,τρ r = αγων,δ (R + r)
acm = αγων,δ R
a = acm (R + r) / R => a = acm (0,8 + 0,4) / 0,8 => a = 3/2 acm
σώμα Σ : ΣF = m a => m g - Τ1 = m a
τροχαλία : Στ(Κ) = Iτρ(Κ) αγων,τρ => Τ1 r - T2 r = Iτρ(Κ) αγων,τρ =>
=> Τ1 r - T2 r = ½ Μτρ r2 αγων,τρ => Τ1 - T2 = ½ Μτρ r αγων,τρ = ½ Μτρ α
δίσκος : ΣF = Mδ acm => Τ2 - Α = Mδ acm
Στ(Ο) = Iδ(Ο) αγων,δ => Τ2 r + Α R = ½ Μδ R2 αγων,δ => Τ2 r/R + Α = ½ Μδ acm => Τ2 / 2 + Α = ½ Μδ acm
m g - Τ1 = m a (1)
Τ1 - T2 = ½ Μτρ α (2)
Τ2 - Α = Mδ acm (3)
Τ2 / 2 + Α = ½ Μδ acm (4) (3) + (4) => 3/2 T2 = 3/2 Μδ acm => T2 = Μδ acm (5)
(1) + (2) + (5) => m g - Τ1 + Τ1 - T2 + T2 = m a + ½ Μτρ α + Μδ acm
=> m g = m 3/2 acm + ½ Μτρ 3/2 αcm + Μδ acm
=> m g = ( 3/2 m + 3/4 Μτρ + Μδ ) acm
=> 4 10 = ( 3/2 4 + 3/4 8 + 8 ) acm
=> 4 10 = ( 6 + 6 + 8 ) acm => acm = 2 m/s2 α = 3/2 2 = 3 m/s2
α = r αγων,τρ => αγων,τρ = α / r = 3 m/s2 / 0,4 m => αγων,τρ = 15/2 rad/s2
acm = αγων,δ R => αγων,δ = acm / R = 2 m/s2 / 0,8 m => αγων,δ = 5/2 rad/s2
m g - Τ1 = m a => 40 - Τ1 = 4 3 => Τ1 = 28 Ν
Τ1 - T2 = ½ Μτρ α => 28 - T2 = ½ 8 3 => T2 = 16 Ν
Τ2 - Α = Mδ acm => 16 - Α = 8 2 => Α = 0
y = ½ α t2 => 24 m = ½ 3 t2 => t = 4 s
xcm = ½ αcm t2 = ½ 2 42 = 16 m
y / xcm = v / vcm = a / acm = 3/2 => y / xcm = 3/2 => 24 m / xcm = 3/2 => xcm = 16 m
ωδ = αγων,δ t = 5/2 4 = 10 rad/s ωτρ = αγων,τρ t = 15/2 4 = 30 rad/s
Kδ = ½ I(O) ωδ2 + ½ Mδ υcm2 = ½ ½ Μδ R2 ωδ2 + ½ Mδ υcm2 =
= 3/4 Μδ R2 ωδ2 = 3/4 8 0,82 102 = 384 J κινητική ενέργεια δίσκου
dKδ /dt = 3/2 Μδ R2 ωδ αγων,δ = 3/2 8 0,82 10 5/2 = 192 J/s
Kτρ = ½ I(Κ) ωτρ2 = ½ ½ Μτρ r2 ωτρ2 = 1/4 8 0,42 302 = 288 J κινητική ενέργεια τροχαλίας
dKτρ /dt = I(Κ) ωτρ αγων,τρ = ½ Μτρ r2 ωτρ αγων,τρ = ½ 8 0,42 30 15/2 = 144 J/s
m g y = 4 10 24 = 960 J δυναμική ενέργεια σώματος Σ
½ m v2 = ½ 4 122 = 288 J κινητική ενέργεια σώματος Σ
960 J = 288 J + 384 J + 288 J 480 J/s = 144 J/s + 192 J/s + 144 J/s
m g y = ½ m v2 + Kδ + Kτρ m g v = m v a + dKδ /dt + dKτρ /dt
33. Ένα ακίνητο στερεό αποτελείται από δύο κατακόρυφους ομοαξονικούς κυλίνδρους κολλημένους μεταξύ τους, ακτίνων R και 3R. Το στερεό μπορεί να περιστρέφεται γύρω από τον κοινό οριζόντιο άξονα των δύο κυλίνδρων ως ένα σώμα. Στην περιφέρεια του κυλίνδρου ακτίνας R έχουμε τυλίξει ένα λεπτό νήμα. Τραβάμε το νήμα οριζόντια από το άκρο του Α με επιτάχυνση μέτρου αΑ = 4 m/s2 ξετυλίγοντάς το χωρίς το νήμα να ολισθαίνει στην επιφάνεια του κυλίνδρου. Τη χρονική στιγμή t0 = 0 το στερεό αρχίζει να κυλίεται στο οριζόντιο έδαφος χωρίς να ολισθαίνει με σταθερή γωνιακή επιτάχυνση.
Δ1. Να βρείτε την επιτάχυνση του κέντρου μάζας του στερεού και την εφαπτομενική επιτάχυνση του σημείου Ε.
Δ2. Αν R = 0,1 m, να βρείτε τη γωνιακή επιτάχυνση του στερεού.
Όταν έχει ξετυλιχτεί νήμα μήκους l = 8 m, να βρείτε:
Δ3. πόσο έχει μετακινηθεί το κέντρο μάζας του στερεού και πόσο το άκρο Α του νήματος.
Δ4. πόση είναι η γωνιακή ταχύτητα του στερεού.
Δ5. πόση είναι η ταχύτητα του ανώτερου σημείου κάθε κυλίνδρου.
Δ1. F R + Τ 3R = I αγων F - Τ = m acm acm = αγων 3R
aA = acm + αγων R = αγων 3R + αγων R => aA = αγων 4R => 4 m/s2 = αγων 4R => 1 m/s2 = αγων R
acm = αγων 3R = 3 m/s2 και αΕ = acm + αγων 3R = αγων 3R + αγων 3R = 6 m/s2
Δ2. 1 m/s2 = αγων R => 1 m/s2 = αγων 0,1 m => αγων = 10 rad/s2
Δ3. l = R θ => 8 m = 0,1 m θ => θ = 80 rad
θ = ½ αγων t2 => 80 = ½ 10 t2 => t2 = 16 => t = 4 s
xcm = ½ αcm t2 = ½ 3 m/s2 16 s2 = 24 m
xA = ½ αA t2 = ½ 4 m/s2 16 s2 = 32 m
Δ4. ω = αγων t = 10 rad/s2 4 s = 40 rad/s υcm = ω 3R = 40 rad/s 0,3 m = 12 m/s
Δ5. υΔ = υcm + ω R = 12 m/s + 40 rad/s 0,1 m = 16 m/s
υE = υcm + ω 3R = 12 m/s + 40 rad/s 0,3 m = 24 m/s
34. Ομογενής και ισοπαχής ράβδος ΑΓ μάζας M = 8 kg και μήκους L = 12,5 m είναι αρθρωμένη σε κατακόρυφο τοίχο. Η δοκός ισορροπεί ακίνητη με την βοήθεια κατακόρυφου αβαρούς και μη εκτατού νήματος το οποίο έχει όριο θραύσης Τθρ=80Ν. Το ένα άκρο του νήματος είναι δεμένο στο άκρο Γ της ράβδου ενώ το άλλο άκρο του είναι στερεωμένο ακλόνητα σε σημείο της οροφής. Η ράβδος σχηματίζει με την οριζόντια διεύθυνση γωνία φ (ημφ = 0,8).
Δ1. Να υπολογίσετε το μέτρο της δύναμης που δέχεται η ράβδος από την άρθρωση.
Στο άκρο Α της ράβδου συγκρατούμε ακίνητο λεπτό τροχό ο οποίος αποτελείται από ομογενή στεφάνη μάζας m1 = 2 kg και ακτίνας R = 0,5 m και δύο ομογενείς ράβδους μήκους l = 2R και μάζας m2 = 1,5 kg η καθεμία.
Δ2. Να υπολογίσετε τη ροπή αδράνειας του τροχού ως προς τον άξονα που διέρχεται από το κέντρο μάζας του και είναι κάθετος στο επίπεδό του.
Αφήνουμε ελεύθερο τον τροχό να κινηθεί, χωρίς να του προσδώσουμε αρχική ταχύτητα. Ο τροχός κυλίεται πάνω στην ράβδο ΑΓ χωρίς να ολισθαίνει και όταν έχει μετατοπιστεί κατά d από την αρχική του θέση, το νήμα κόβεται.
Δ3. Να υπολογίσετε την απόσταση d και το χρόνο που θα χρειαστεί για να κοπεί το νήμα, αν δίνεται ότι η επιτάχυνση του κέντρου μάζας του τροχού κατά την κάθοδό του είναι αcm=5m/s2. Επιπλέον, να γραφεί η σχέση που δίνει την τάση του νήματος σε συνάρτηση με το χρόνο T=f(t), μέχρι τη στιγμή που κόβεται το νήμα.
Δ4. Να γραφεί η σχέση που δίνει τον αριθμό των περιστροφών του τροχού σε συνάρτηση με το χρόνο Ν=f(t) και να γίνει η αντίστοιχη γραφική παράσταση.
35. Δίνεται συμπαγής, ομογενής κύλινδρος μάζας Μ και ακτίνας R. Αφήνουμε τον κύλινδρο να κυλίσει χωρίς ολίσθηση, υπό την επίδραση της βαρύτητας (με επιτάχυνση της βαρύτητας g), πάνω σε κεκλιμένο επίπεδο γωνίας φ, όπως φαίνεται στο σχήμα που ακολουθεί:
Δ1. Να υπολογίσετε την επιτάχυνση του κέντρου μάζας του κυλίνδρου.
Ο άξονας του κυλίνδρου διατηρείται οριζόντιος.
Δ2. Από το εσωτερικό αυτού του κυλίνδρου, που έχει ύψος h, αφαιρούμε πλήρως ένα ομοαξονικό κύλινδρο ακτίνας r, όπου r < R, όπως απεικονίζεται στο σχήμα. Να αποδείξετε ότι η ροπή αδράνειας του κοίλου κυλίνδρου, ως προς τον άξονα του, που προκύπτει μετά την αφαίρεση του εσωτερικού κυλινδρικού τμήματος, είναι : Iκοίλου κυλίνδρου = ½ M R2 ( 1 - r4/R4 )
Στη συνέχεια λιπαίνουμε το κυλινδρικό τμήμα που αφαιρέσαμε και το επανατοποθετούμε στη θέση του, ούτως ώστε να εφαρμόζει απόλυτα με τον κοίλο κύλινδρο χωρίς τριβές. Το νέο σύστημα που προκύπτει αφήνεται να κυλίσει χωρίς ολίσθηση, υπό την επίδραση της βαρύτητας (με επιτάχυνση της βαρύτητας g), στο ίδιο κεκλιμένο επίπεδο, όπως φαίνεται στο σχήμα.
Δ3. Να υπολογίσετε την επιτάχυνση του κέντρου μάζας του συστήματος.
Δ4. Όταν r = R/2, να υπολογίσετε, σε κάθε χρονική στιγμή της κύλισης στο κεκλιμένο επίπεδο, το λόγο της μεταφορικής προς την περιστροφική κινητική ενέργεια του συστήματος.
Ο άξονας του συστήματος διατηρείται πάντα οριζόντιος.
Δίνονται : Η ροπή αδράνειας Ι συμπαγούς και ομογενούς κυλίνδρου μάζας Μ και ακτίνας R, ως προς τον άξονα γύρω από τον οποίο στρέφεται: Ι = 1/2 M R2
Ο όγκος V ενός συμπαγούς κυλίνδρου ακτίνας R και ύψους h: V = π R2 h
 Στ(Κ) = Ι(Κ) αγων => Τ R = ½ Μ R2 αγων => Τ = ½ Μ R αγων = ½ Μ α
Στ(Κ) = Ι(Κ) αγων => Τ R = ½ Μ R2 αγων => Τ = ½ Μ R αγων = ½ Μ α
ΣF = M a => Μ g ημφ - Τ = Μ α => Μ g ημφ - ½ Μ α = Μ α => Μ g ημφ = 3/2 Μ α => α = 2/3 g ημφ
Μ = ρ V = ρ π R2 h m = ρ V' = ρ π r2 h m / M = ( r / R )2
Iκοίλου κυλίνδρου = ½ M R2 - ½ m r2 = ½ M R2 - ½ M ( r / R )2 r2 = ½ M R2 [ 1 - (r / R)4 ]
το κυλινδρικό τμήμα που επανατοποθετούμε δεν μπορεί να περιστραφεί διότι δεν υπάρχει τριβή ούτε ροπή για να το περιστρέψει συνεπώς θα εκτελέσει μόνο μεταφορική κίνηση, το κοίλο τμήμα του κυλίνδρου θα εκτελέσει και μεταφορική και περιστροφική κίνηση
Στ(Κ) = Iκοίλου κυλίνδρου αγων => Τ R = ½ M R2 [ 1 - (r / R)4 ] αγων =>
=> Τ = ½ Μ R [ 1 - (r / R)4 ] αγων = ½ Μ α [ 1 - (r / R)4 ]
ΣF = M a => Μ g ημφ - Τ = Μ α => Μ g ημφ - ½ Μ α [ 1 - (r / R)4 ] = Μ α =>
=> Μ g ημφ = [ 3/2 - (r / R)4 ] Μ α => α = g ημφ / [ 3/2 - (r / R)4 ]
για r = R/2 έχουμε:
Iκοίλου κυλίνδρου = ½ M R2 - ½ m r2 = ½ M R2 - ½ M ( r / R )2 r2 = ½ M R2 [ 1 - (r / R)4 ] =
= ½ M R2 [ 1 - (1/2)4 ] = ½ M R2 [ 1 - 1/16 ] = ½ M R2 15/16
α = g ημφ / [ 3/2 - (r / R)4 ] = g ημφ / [ 3/2 - (1/2)4 ] = g ημφ / [ 3/2 - 1/16 ] = 16/23 g ημφ
υ = α t = 16/23 g ημφ t ω = υ/R = 16/23 g/R ημφ t
Κμεταφορική = ½ Μ υ2 = ½ Μ ( 16/23 g ημφ t )2
Κπεριστροφική = ½ Iκοίλου κυλίνδρου ω2 = ½ ½ Μ R2 15/16 ( υ/R )2 = 1/4 Μ 15/16 υ2
Κμεταφορική / Κπεριστροφική = 32/15
36. Θέλουμε να μετρήσουμε πειραματικά την άγνωστη ροπή αδράνειας δίσκου μάζας Μ = 3 kg και ακτίνας R = 1 m. Για το σκοπό αυτό αφήνουμε τον δίσκο να κυλίσει χωρίς ολίσθηση σε κεκλιμένο επίπεδο γωνίας κλίσεως φ = 30° ξεκινώντας από την ηρεμία. Διαπιστώνουμε ότι ο δίσκος διανύει την απόσταση x = 2 m σε χρόνο t = 1 s.
Δ1. Να υπολογίσετε την ροπή αδράνειας του δίσκου ως προς τον άξονα περιστροφής που διέρχεται από το κέντρο μάζας του και είναι κάθετος στο επίπεδό του.
Δ2. Από την κορυφή του κεκλιμένου επιπέδου αφήνονται να κυλίσουν ταυτόχρονα δίσκος και δακτύλιος ίδιας μάζας Μ και ίδιας ακτίνας R. Η ροπή αδράνειας του δίσκου είναι Ι1 = ½ Μ R2 και του δακτυλίου Ι2 = Μ R2 ως προς τους άξονες που διέρχονται από τα κέντρα μάζας τους και είναι κάθετοι στα επίπεδά τους. Βρείτε ποιό από τα σώματα κινείται με την μεγαλύτερη επιτάχυνση.
Συνδέουμε με κατάλληλο τρόπο τα κέντρα μάζας των δύο στερεών με ράβδο αμελητέας μάζας η οποία δεν εμποδίζει την περιστροφή τους και δεν ασκεί τριβές. Το σύστημα κυλίεται στο κεκλιμένο επίπεδο χωρίς να ολισθαίνει.
Δ3. Υπολογίστε τον λόγο των κινητικών ενεργειών Κ1 / Κ2 όπου Κ1 η κινητική ενέργεια του δίσκου και Κ2 η κινητική ενέργεια του δακτυλίου.
Δ4. Αν η μάζα κάθε στερεού είναι Μ = 1,4 kg υπολογίστε τις δυνάμεις που ασκεί η ράβδος σε κάθε σώμα.
ΑΣΚΗΣΗ 1
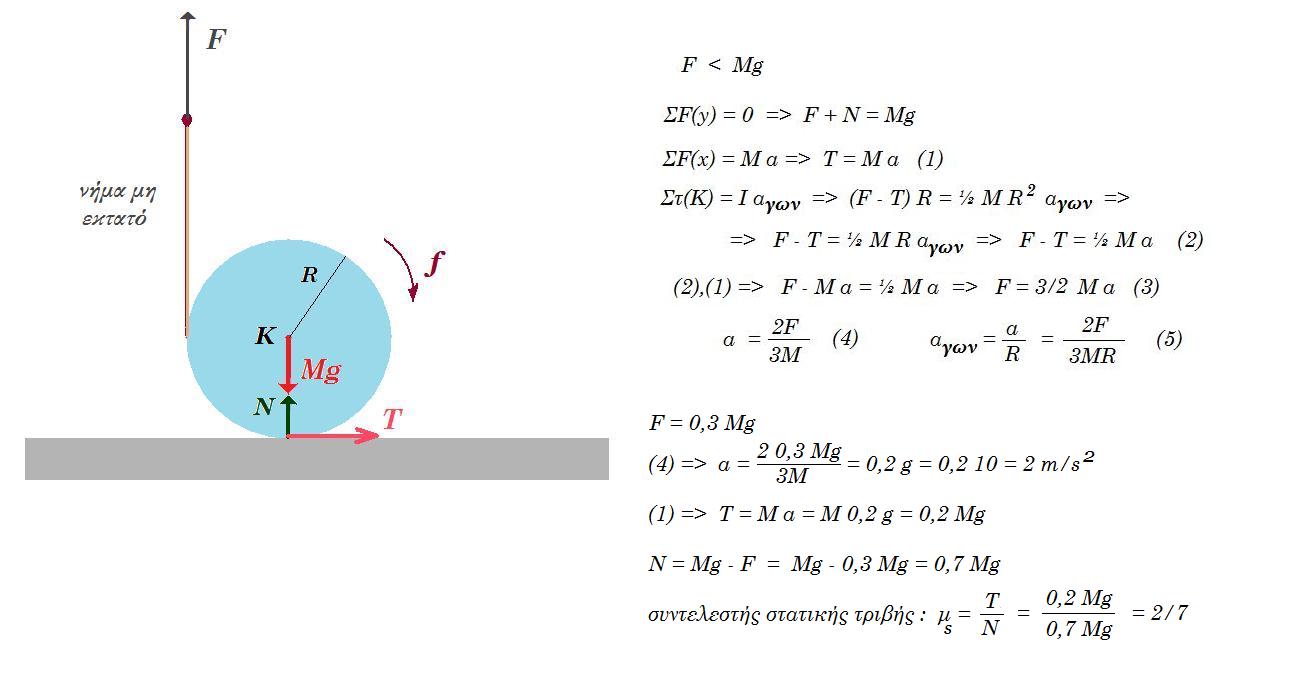
ΑΣΚΗΣΗ 2
Το στερεό του σχήματος αποτελείται από δύο ομοαξονικούς κυλίνδρους, με ακτίνες R1 = 4 cm και R2 = 3 cm, που στέφονται γύρω από σταθερό άξονα x’x. 
Ο άξονας x’x συμπίπτει με τον άξονα συμμετρίας των κυλίνδρων. Εξ αιτίας των βαρών που κρέμονται από τους δύο κυλίνδρους, τα σκοινιά ασκούν στους κυλίνδρους δυνάμεις F1 = 6 Ν και F2 = 10 Ν.
Να υπολογίσετε την ολική ροπή που δέχεται το στερεό.
Στ = F1 . R1 - F2 . R2 = 6 N . 0,04 m - 10 N . 0,03 m = 0,24 N.m - 0,3 N.m = - 0,06 N.m το σύστημα των κυλίνδρων δεν ισορροπεί, θα στραφεί κατά την φορά της F2
ΑΣΚΗΣΗ 3
Στην περιφέρεια μιας ακίνητης τροχαλίας, ακτίνας R = 20 cm, είναι τυλιγμένο σκοινί. Ασκώντας στο σκοινί οριζόντια δύναμη F = 20π Ν περιστρέφουμε την τροχαλία. Βρέθηκε ότι όταν η τροχαλία έχει κάνει τέσσερις περιστροφές έχει γωνιακή ταχύτητα ω = 8π rad/s.  Να υπολογιστεί η μάζα της. Δίνεται ότι η ροπή αδράνειας της τροχαλίας ως προς τον άξονα περιστροφής της είναι I=1/2·m·R2.
Να υπολογιστεί η μάζα της. Δίνεται ότι η ροπή αδράνειας της τροχαλίας ως προς τον άξονα περιστροφής της είναι I=1/2·m·R2.
ΛΥΣΗ
θ = 4 . 2π = 8π rad ω = αγων . t = 8π rad/s
θ = 0,5 . αγων . t2 => θ = 0,5 . αγων . t . t => 8π rad = 0,5 . 8π rad/s . t => t = 2 sec
άρα aγων = ω/t = 4π rad/s2
τ = I . aγων => F . R = 0,5 . M . R2 . aγων => F = 0,5 . M . R . aγων =>
=> 20π Ν = 0,5 . M . 0,2 m . 4π rad/s2 => M = 50 kg

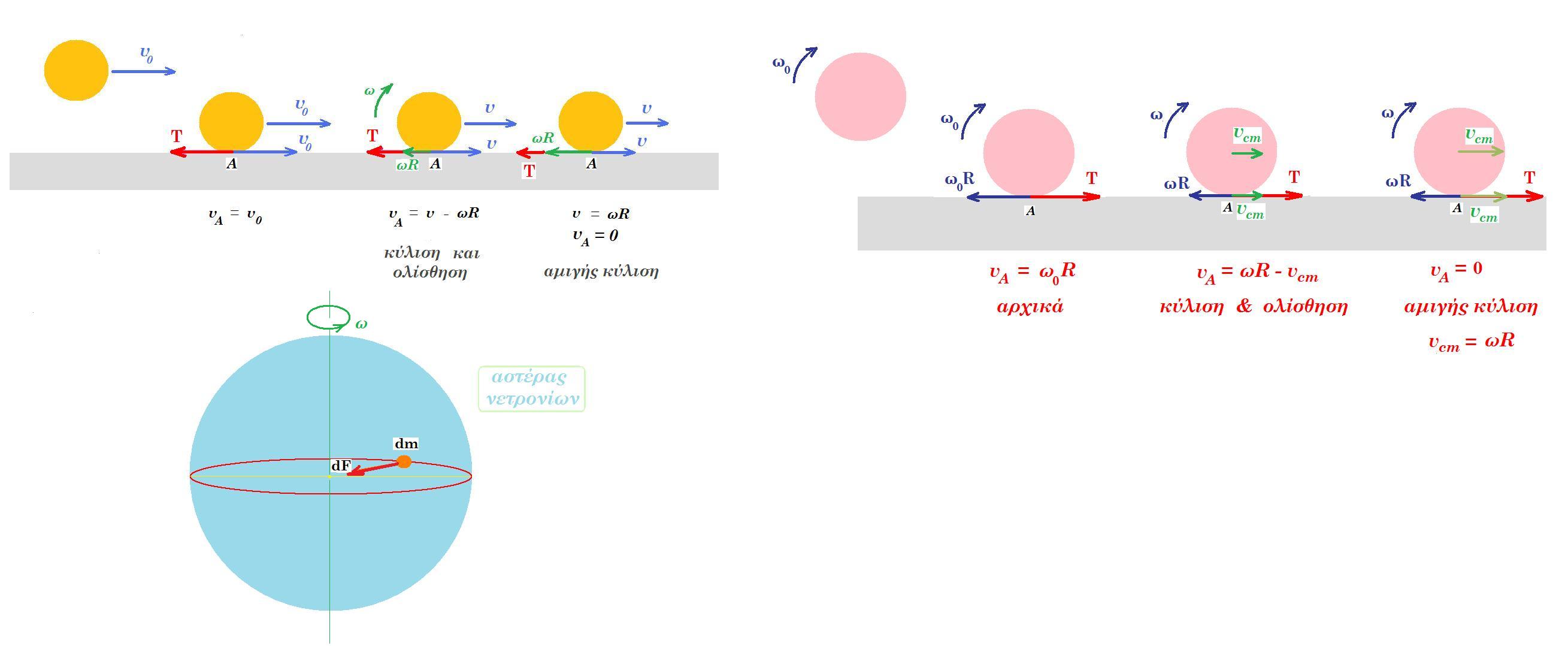
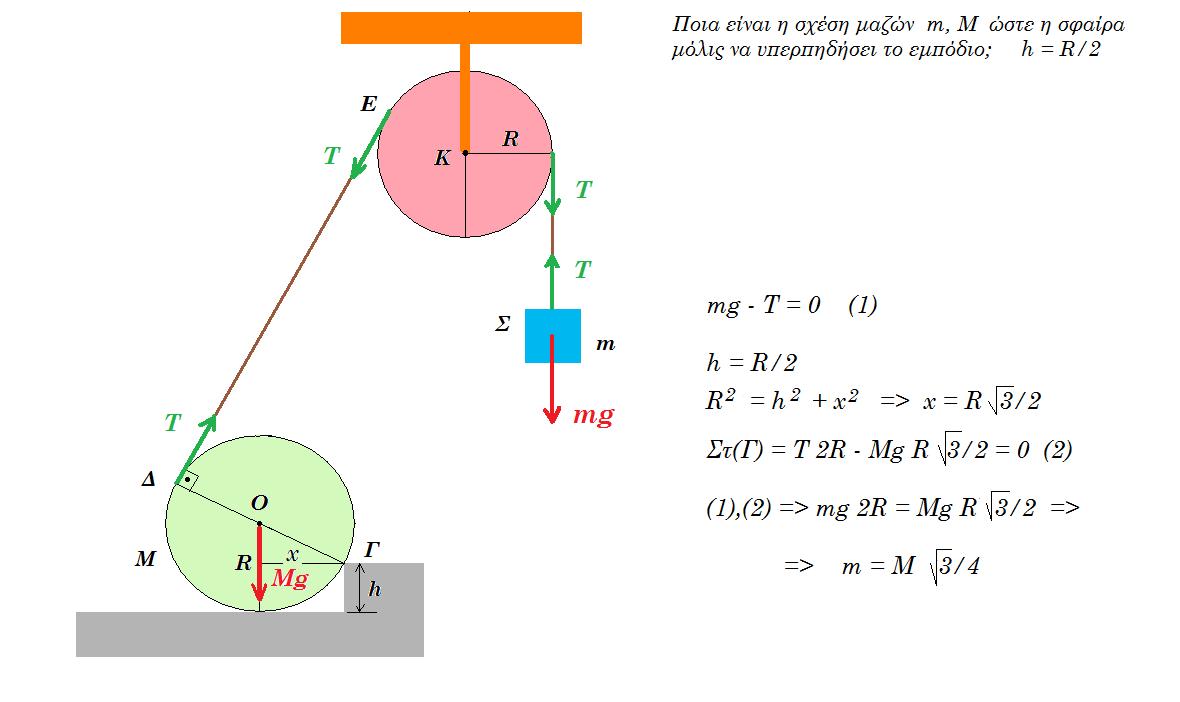
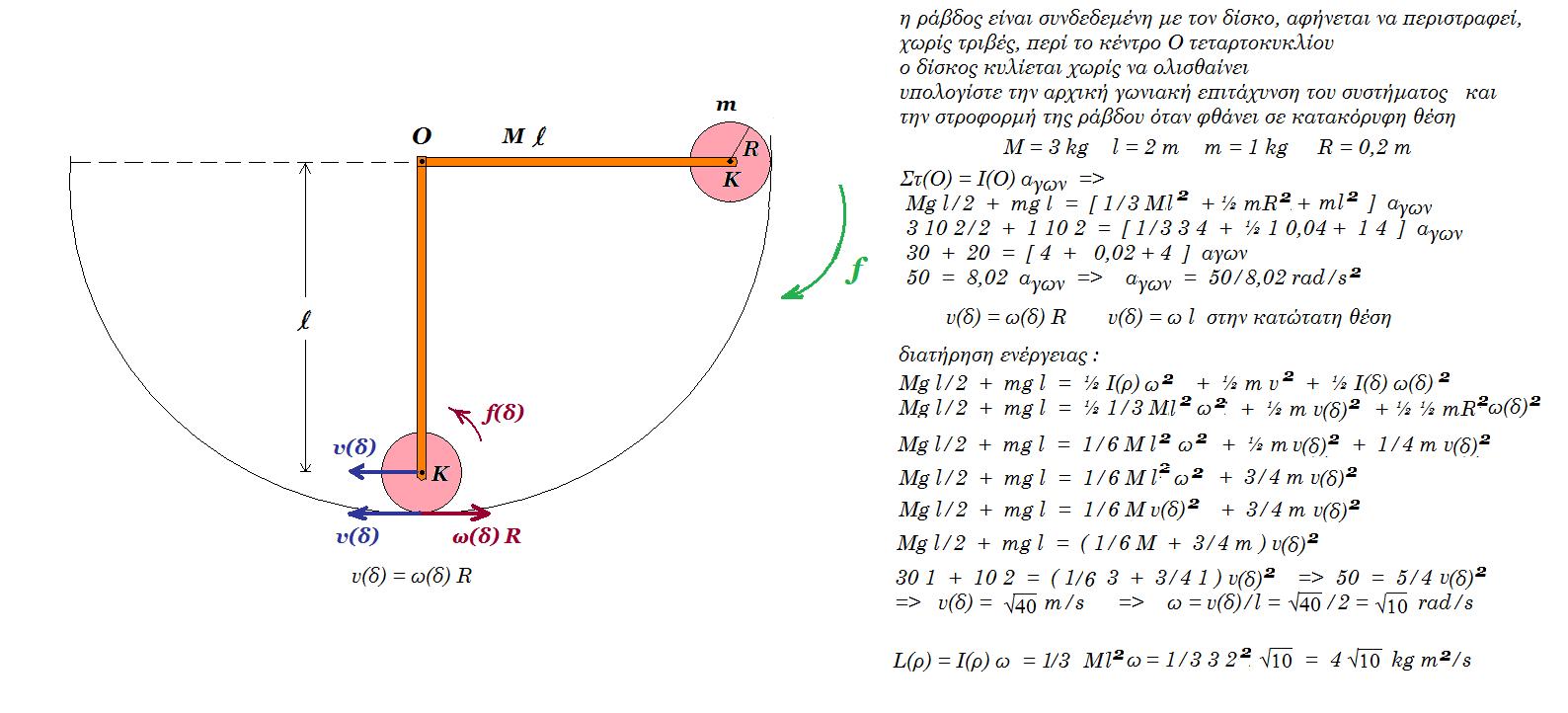


Ομογενής σφαίρα μάζας m και ακτίνας r ισορροπεί στο άνω άκρο σφαίρας μάζας Μ και ακτίνας R. Κάποια στιγμή η σφαίρα κυλίεται χωρίς να ολισθαίνει πάνω στην σφαιρική επιφάνεια. Βρείτε την γωνία θ που σχηματίζει η διάκεντρος των σφαιρών την στιγμή που η μικρή σφαίρα χάνει την επαφή της με την μεγάλη σφαίρα.
ΣFr = Fκ => mg συνθ - Ν = m v2 / (r + R)
όταν η σφαίρα m χάνει την επαφή με την σφαιρική επιφάνεια ισχύει Ν = 0 οπότε
mg συνθ = m v2 / (r + R) => v2 = g (r + R) συνθ
διατήρηση ενέργειας :
m g { r + R - (r + R) συνθ } = ½ m v2 + ½ I ω2
m g (r + R) (1 - συνθ) = ½ m v2 + ½ 2/5 m r2 ω2
m g (r + R) (1 - συνθ) = 1/2 m v2 + 1/5 m v2
m g (r + R) (1 - συνθ) = 7/10 m v2
g (r + R) (1 - συνθ) = 7/10 v2
g (r + R) (1 - συνθ) = 7/10 g (r + R) συνθ
(r + R) (1 - συνθ) = 7/10 (r + R) συνθ
1 - συνθ = 7/10 συνθ
1 = 7/10 συνθ + συνθ
συνθ = 10/17
ΑΣΚΗΣΗ 14
Ομογενής σφαίρα μάζας m και ακτίνας r αφήνεται να κυλίσει από σημείο Α κεκλιμένου επιπέδου γωνίας κλίσεως θ. Όταν φθάνει στη βάση Β του κεκλιμένου ακολουθεί ημικυκλική επιφάνεια ακίνας R. Από ποιό ύψος h πρέπει να αφεθεί η σφαίρα έτσι ώστε μόλις να διέλθει από την ανώτερη θέση Δ; Πόση δύναμη δέχεται η σφαίρα όταν διέρχεται από τις θέσεις Β και Γ από την ημικυκλική επιφάνεια; 
διατήρηση ενέργειας :
m g ( h + r συνθ ) = ½ m vΔ2 + ½ I ω2 + m g ( 2R - r )
m g ( h + r συνθ ) = ½ m vΔ2 + ½ 2/5 m r2 ω2 + m g ( 2R - r )
g ( h + r συνθ ) = 1/2 vΔ2 + 1/5 vΔ2 + g ( 2R - r )
g ( h + r συνθ ) - g ( 2R - r ) = 7/10 vΔ2
g ( h + r + r συνθ - 2R ) = 7/10 vΔ2 (1)
όταν η σφαίρα διέρχεται από την ανώτερη θέση Δ : ΣFy = Fκ => mg + Ν = m vΔ2 / (R - r)
μόλις διέρχεται ισχύει Ν = 0 οπότε mg = m vΔ2 / (R - r) => vΔ2 = g (R - r) (2)
(1) , (2) => g ( h + r + r συνθ - 2R ) = 7/10 g (R - r) =>
=> 10 ( h + r + r συνθ - 2R ) = 7 (R - r) =>
=> 10 h = 7 (R - r) - 10 (r + r συνθ) + 20 R =>
=> 10 h = 27 R - 17 r - 10 r συνθ =>
=> h = 2,7 R - (1,7 + συνθ) r (3) h + r συνθ = 2,7 R - 1,7 r
όταν η σφαίρα διέρχεται από την κατώτερη θέση Β : ΣFy = Fκ => Ν(Β) - mg = m vΒ2/ (R - r) (4)
διατήρηση ενέργειας :
m g ( h + r συνθ ) = ½ m vΒ2 + ½ I ω2 + m g r
m g ( h + r συνθ ) = ½ m vΒ2 + ½ 2/5 m r2 ω2 + m g r
m g ( h + r συνθ ) = 7/10 m vΒ2 + m g r από (3) έχουμε
g ( 2,7 R - 1,7 r - r ) = 7/10 vΒ2
g { 2,7 R - 2,7 r } = 7/10 vΒ2 => 27/7 g(R - r) = vΒ2 (5)
(4) , (5) => Ν(Β) = mg + 27/7 mg => Ν(Β) = 34/7 mg
όταν η σφαίρα διέρχεται από την θέση Γ : ΣFx = Fκ => Ν(Γ) = m vΓ2/ (R - r) (4)
διατήρηση ενέργειας :
m g ( h + r συνθ ) = ½ m vΓ2 + ½ I ω2 + m g R
m g ( h + r συνθ ) = ½ m vΓ2 + ½ 2/5 m r2 ω2 + m g R
m g ( h + r συνθ ) = 7/10 m vΓ2 + m g R από (3) έχουμε
g ( 2,7 R - 1,7 r - R ) = 7/10 vΓ2
g { 1,7 R - 1,7 r } = 7/10 vΓ2 => 17/7 g(R - r) = vΓ2 (5)
(4) , (5) => Ν(Γ) = 17/7 mg => Ν(Γ) = 17/7 mg

h = 2,7 R - (1,7 + συνθ) r = 2,7 1 - (1,7 + 0,8) 0,1 = 2,7 - 0,25 = 2,45 m
αν R = 1 m m = 3 kg r = 0,1 m υΔ2 = g (R - r) = 10 (1 - 0,1) = 9 => υΔ = 3 m/s
η σφαίρα στον αέρα δεν δέχεται δύναμη που να δημιουργεί ροπή συνεπώς η γωνιακή ταχύτητά του είναι σταθερή ω = υΔ / r = 3 m/s / 0,1 m = 30 rad/s
το κέντρο μάζας της σφαίρας εκτελεί οριζόντια βολή
x = υ0 t = vΔ t = 3 m/s 0,2 s = 0,6 m
y = h = ½ g t2 = ½ 10 0,22 = 0,2 m
αν θεωρήσουμε ως αρχή των αξόνων Ο(0,0) την θέση Δ την χρονική στιγμή t = 0, το κέντρο μάζας της σφαίρας την χρονική στιγμή t = 0,2 s βρίσκεται αριστερά και κάτω από την θέση Δ, στην θέση με συντεταγμένες : (x , y) = ( - 0,6 m , - 0,2 m )
η ταχύτητά του είναι :
vy = g t = 10 0,2 => vy = 2 m/s
v2 = vx2 + vy2 = 32 + 22 = 9 + 4 = 13 => v = Φ13 m/s
η στροφορμή της σφαίρας είναι L = Icm ω = 2/5 m r2 ω = 2/5 3 0,12 30 = 0,36 kg m2/s
ο ρυθμός μεταβολής της στροφορμής είναι : dL/dt = Στcm = 0
η γωνιακή επιτάχυνση της σφαίρας είναι : Icm αγων = Στcm = 0 => αγων = 0
ο ρυθμός μεταβολής κινητική ενέργειας λόγω περιστροφής : dΚ/dt = Icm αγων ω = 0
διατήρηση ενέργειας M g h + ½ M υΔ2 + ½ I(O) ω2 = ½ M υ2 + ½ I(O) ω2
Μ g h + ½ M υΔ2 = ½ M υ2
g h + ½ υΔ2 = ½ υ2 => 10 0,2 + ½ 32 = ½ υ2 => υ2 = 13
όταν η σφαίρα διέρχεται από την θέση Ζ : ΣFx = Fκ => Ν(Ζ) = m vΖ2/ (R - r) (4)
διατήρηση ενέργειας :
m g ( h + r συνθ ) = ½ m vΖ2 + ½ I ω2 + m g R
m g ( h + r συνθ ) = ½ m vΖ2 + ½ 2/5 m r2 ω2 + m g R
m g ( h + r συνθ ) = 7/10 m vΖ2 + m g R από (3) έχουμε
g ( 2,7 R - 1,7 r - R ) = 7/10 vΖ2
g { 1,7 R - 1,7 r } = 7/10 vΖ2 => 17/7 g(R - r) = vΖ2 (5)
(4) , (5) => Ν(Ζ) = 17/7 mg => Ν(Ζ) = 17/7 mg
κεντρομόλος επιτάχυνση : ακ = vΖ2/ (R - r) = 17/7 g
στην θέση Ζ η σφαίρα δέχεται την δύναμη βαρύτητας και την δύναμη Ν(Ζ) από το ημικύκλιο που είναι μεταξύ τους κάθετες
συνολικά : ΣF2 = (mg)2 + Ν(Ζ)2 = (mg)2 + (17/7 mg)2 = [ 1 + (17/7)2 ] (mg)2 =>
=> ΣF = [ 1 + (17/7)2 ]½ mg = m α => a = g [ 1 + (17/7)2 ]½ η επιτάχυνση της σφαίρας όταν διέρχεται από την θέση Ζ
Βπην = 4π 10-7 i n => 4π 10-3 = 4π 10-7 i 1000 => i = 10 A
FL = B i l => 1 = B 10 1 => B = 0,1 Tesla με φορά προς τα έξω
ΘΈΜΑ Δ.
Θεωρούμε την διάταξη του σχήματος, σε κατάσταση ισορροπίας, σε κατακόρυφο επίπεδο. Στη θέση Α του κεκλιμένου επιπέδου ισορροπεί σφαίρα μάζας m = 3 kg , ακτίνας r = 0,1 m και ροπής αδράνειας Icm = 2/5 m r2. Το κεκλιμένο επίπεδο γωνίας κλίσεως θ, όπου ημθ = 0,6 και συνθ = 0,8 στην βάση του συνδέεται με κατακόρυφο ημικύκλιο ακτίνας R = 1 m. Η σφαίρα στο άνω της άκρο συνδέεται με οριζόντιο, αβαρές, μη εκτατό νήμα 1 (σταθερού μήκους), με τροχαλία μάζας Μ = 5 kg εσωτερικής ακτίνας rτροχ = 0,2 m , εξωτερικής ακτίνας Rτροχ = 0,5 m και ροπής αδράνειας Ιcm = ½ M Rτροχ2 . Γύρω από την τροχαλία έχουμε τυλίξει αρκετές φορές αβαρές μη εκτατό νήμα 2 το οποίο συνδέεται με την μεταλλική ράβδο ΚΛ στο μέσον αυτής. Η μεταλλική ράβδος ισορροπεί σε οριζόντια θέση, έχει μήκος l = 1 m και μάζα m = 0,5 kg, είναι σε επαφή με κατακόρυφους αγωγούς Mx, Ny. Το πηνίο φέρει 1000 σπείρες / m, διαρρέεται από συνεχές ρεύμα εντάσεως Ι, στο κέντρο του το μέτρο της εντάσεως του μαγνητικού πεδίου είναι Βπην = 4π 10-3 Tesla. Στον γραμμοσκιασμένο χώρο abcd υπάρχει οριζόντιο ομογενές μαγνητικό πεδίο εντάσεως Β.
Δ1. Βρείτε την ένταση Β του ομογενούς μαγνητικού πεδίου Β. 5
Κάποια στιγμή κόβουμε το νήμα 1 και ταυτόχρονα ανοίγουμε τον διακόπτη δ, οπότε η σφαίρα κατέρχεται του κεκλιμένου επιπέδου κυλιόμενη ( μη ολισθαίνουσα ) ενώ η ράβδος κινείται κατακόρυφα προς τα κάτω ενώ είναι συνεχώς σε επαφή με τους αγωγούς Mx, Ny.
Δ2. Εξηγείστε γιατί φορτίζεται η ράβδος ΚΛ κατερχόμενη. Εκφράστε την τάση στα άκρα της συναρτήσει του χρόνου. 5
Δ3. Η σφαιρα κυλίεται ( δεν ολισθαίνει ) κινούμενη στο κεκλιμένο επίπεδο, διέρχεται από την θέση Γ, ανέρχεται κυλιόμενη στο ημικύκλιο και μόλις διέρχεται από την ανώτατη Δ του ημικυκλίου. 5
Δ3 (α) Βρείτε το ύψος h έτσι ώστε η σφαίρα μόλις διέρχεται από την ανώτατη Δ του ημικυκλίου. 5
Δ3 (β) Θεωρώντας ως αρχή των αξόνων Ο(0,0) την θάση Δ την χρονική στιγμή t = 0 βρείτε τις συντεταγμένες του κέντρου μάζας της σφαίρας την χρονική στιγμή t = 0,2 s, την στροφορμή της και τον ρυθμό μεταβολής της κινητικής της ενέργειας λόγω περιστροφής. 4 + 3 + 3
Δ3 (γ) Βρείτε την επιτάχυνση της σφαίρας όταν διέρχεται από την θέση Ζ του σχήματος. 5
ΑΣΚΗΣΗ 16
Λεπτή, άκαμπτη και ομογενής ράβδος ΑΓ μήκους l = 1,2 m και μάζας M = 1 kg μπορεί να περιστρέφεται σε κατακόρυφο επίπεδο, χωρίς τριβές, γύρω από σταθερό οριζόντιο άξονα κάθετο στη ράβδο, ο οποίος διέρχεται από το σημείο Ο σε απόσταση l/3 από το άκρο Α της ράβδου. Το άκρο Γ της ράβδου συνδέεται με αβαρές νήμα που σχηματίζει γωνία φ = 30° με τη ράβδο, το άλλο άκρο του οποίου είναι ακλόνητα συνδεδεμένο σε σταθερό σημείο Δ όπως στο σχήμα.
Το σύστημα αρχικά ισορροπεί σε οριζόντια θέση. Κάποια στιγμή το νήμα κόβεται.
Γ1. Να υπολογίσετε το μέτρο της δύναμης που ασκεί το νήμα στη ράβδο και το μέτρο της δύναμης που δέχεται η ράβδος από τον άξονα περιστροφής Ο, πριν κοπεί το νήμα.
Γ2. Να υπολογίσετε
α) τη ροπή αδράνειας της ράβδου ως προς τον άξονα περιστροφής της
β) τη γωνιακή επιτάχυνση της ράβδου τη χρονική στιγμή κατά την οποία κόβεται το νήμα.
Γ3. Να υπολογίσετε την ταχύτητα του άκρου Γ της ράβδου τη χρονική στιγμή κατά την οποία η ράβδος διέρχεται για πρώτη φορά από την κατακόρυφη θέση.
Γ4. Να υπολογίσετε το μέτρο του ρυθμού μεταβολής της στροφορμής της ράβδου τη χρονική στιγμή που σχηματίζει γωνία 30° με την κατακόρυφο, μετά τη διέλευσή της για πρώτη φορά από την κατακόρυφη θέση.
ροπές ως προς Ο : M g (l/2 - l/3) - Τ ημ30° 2l/3 = 0 => M g l/6 = Τ ½ 2l/3 => 1 10 l/2 = Τ => Τ = 5 Ν Tx = Τ συν30° = Φ3/2 Χ 5 N = 2,5ΧΦ3 N
ΣFx = 0 => Fx = Tx = 2,5ΧΦ3 N
ΣFy = 0 => M g - Ty - Fy = 0 => M g - T ημ30° = Fy => 10 - 5 ½ = Fy => Fy = 7,5Ν
ροπή αδράνειας της ράβδου ως προς τον άξονα περιστροφής της που διέρχεται από το σημείο Ο : Ι(Ο) = 1/12 Μ l2 + M (l/2 - l/3)2 = 1/12 Μ l2 + M (l/6)2 = 1/9 Μ l2 = 1/9 1 1,22 =0,16 kg m2
Στ(Ο) = Ι(Ο) αγων => M g (l/2 - l/3) = Ι(Ο) αγων => M g l/6 = Ι(Ο) αγων => 10 1,2/6 = 0,16 αγων => αγων = 2/0,16 = 12,5 rad/s2
διατήρηση ενέργειας : M g l/6 = ½ Ι(Ο) ω2 => 10 1,2/6 = ½ 0,16 ω2 => 2 / 0,08 = ω2 => ω = 5 rad/s γωνιακή ταχύτητα ράβδου όταν διέρχεται από την κατώτατη θέση για 1η φορά
ταχύτητα του άκρου Γ : υ(Γ) = ω 2l/3 = 5 2 1,2 / 3 = 4 m/s
ρυθμός μεταβολής στροφορμής : dL/dt = Στ(Ο) = M g (l/2 - l/3) ημ30° = 10 1,2/6 ½ = 1 Nm = Ι(Ο) αγων = 0,16 αγων => αγων = 1/0,16 = 6,25 rad/s2 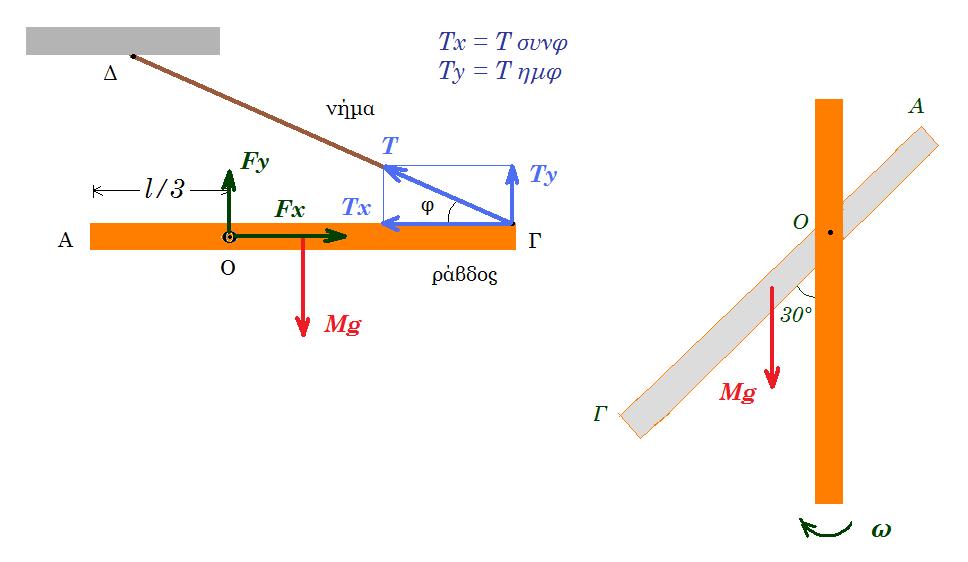
ΑΣΚΗΣΗ 17
ΑΣΚΗΣΗ 18
 m = 3 kg M = 6 kg r = R/2
m = 3 kg M = 6 kg r = R/2
r αγων = a2 a1 = R αγων + a2 = (R + r) αγων = 3r αγων = 3 a2 r = R/2
m g - T1 = m a1 (1) M g + T1 - T2 = M a2 (2)
T1 R + T2 r = ½ M R2 αγων => 2 T1 + T2 = M R αγων (3)
(2) + (3) => M g + 3 T1 = M a2 + M R αγων = 2 M a2 (4)
3*(1) + (4) => 3 m g + M g = 3 m a1 + 2 M a2
=> 3 m g + M g = 3 m 3 a2 + 2 M a2
=> 3 m g + M g = ( 9 m + 2 M ) a2
=> 3 3 10 + 6 10 = ( 9 3 + 2 6 ) a2 => a2 = 150/45 = 10/3 m/s2
οπότε a1 = 10 m/s2
(1) => T1 = m g - m a1 = 3 10 - 3 10 = 0
(2) => T2 = M g + T1 - M a2 = 6 10 + 0 - 6 10/3 = 40 Ν
Κτροχαλίας = ½ Μ υ2 + ½ ½ Μ R2 ω2 =
= ½ Μ α22 t2 + ½ ½ Μ R2 αγων2 t2 =
= ½ Μ α22 t2 + 1/4 Μ R2 α22 / r2 t2 =
= ½ Μ α22 t2 + 1/4 Μ 4 α22 t2 =
= 3/2 Μ α22 t2 = 3/2 6 100/9 9 = 900 Joule t = 3 sec