
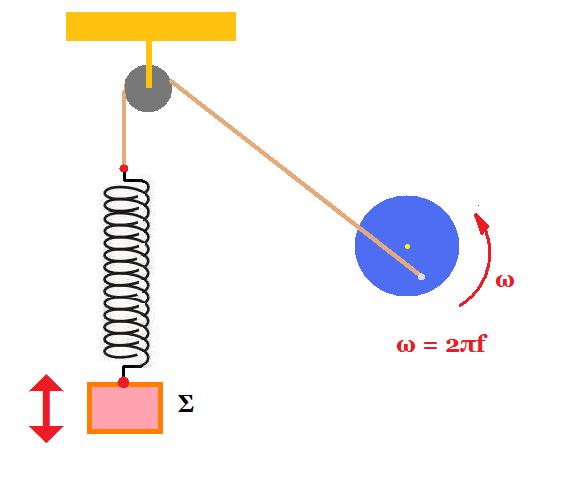
Απλός αρμονικός ταλαντωτής, ελατήριο σταθεράς K = 100 N/m και σώμα μάζας m = 1 kg εκτελεί εξαναγκασμένη ταλάντωση με συχνότητα διεγέρτη f = 8/π Ηz. Αν η συχνότητα του διεγέρτη αυξηθεί, τότε το πλάτος της ταλάντωσης
(α) μειώνεται (β) αυξάνεται (γ) μένει σταθερό
k = m . ω2 => 100 N/m = 1 kg . ω2 => ω = 10 rad/s => 2π.f0 = 10 rad/s => f0 = 5/π Hz ιδιοσυχνότητα του ταλαντωτή
η συχνότητα του διεγέρτη είναι μεγαλύτερη από την ιδιοσυχνότητα του ταλαντωτή,
αν η συχνότητα του διεγέρτη αυξηθεί, τότε το πλάτος της ταλάντωσης μειώνεται
Ελατήριο που εκτελεί εξαναγκασμένες ταλαντώσεις έχει σταθερά k = 162 Ν/m και το σώμα μάζα m=0,5kg. Το σώμα σε χρόνο t = 10π s διέρχεται 90 φορές από τη θέση ισορροπίας του. Τότε η κυκλική συχνότητα του διεγέρτη τροχού είναι:
(α) 9 rad/s (β) 18 rad/s, (γ) 17 rad/s
Για να συντονιστεί το σύστημα πρέπει η συχνότητα του διεγέρτη να
(α) αυξηθεί κατά 100%. (β) μειωθεί κατά 50%, (γ) μείνει σταθερή, (δ) αυξηθεί κατά 50%
k = m . ω2 => 162 N/m = 0,5 kg . ω2 => ω = Φ324 rad/s = 18 rad/s => 2π.f0 = 18 rad/s => f0 = 9/π Hz ιδιοσυχνότητα του ταλαντωτή
επειδή το σώμα σιέρχεται 90 φορές από τη θέση ισορροπίας του σημαίνει ότι εκτελεί 45 ταλαντώσεις (κύκλους) σε χρόνο 10.π s οπότε η συχνότητα του διεγέρτη είναι fδ = 45 / 10π = 9/2π Hz άρα η κυκλική συχνότητα του διεγέρτη είναι ωδ = 2π.f = 9 rad/s
για να συντονιστεί το σύστημα πρέπει fδ = f0 δηλαδή πρέπει να αυξηθεί η συχνότητα του διεγέρτη από 9/2π Hz σε 9/π Hz δηλαδή αύξηση 9/2π Hz άρα 100 %
** Σε μια εξαναγκασμένη ταλάντωση η συχνότητα του διεγέρτη είναι fδ και είναι ίση με fδ = 2 f0.
(Α) Ο λόγος της μέγιστης δυναμικής προς τη μέγιστη κινητική ενέργεια της ταλάντωσης είναι:
(α) Umax / Kmax = 1/4 (β) Umax / Kmax = 1/2 (γ) Umax / Kmax = 2
(Β) Για ποια τιμή της fδ ο προηγούμενος λόγος θα γίνει ίσος με 1;
(α) fδ = f0 / 2 (β) fδ = f0 / 4 (γ) fδ = f0
Umax = ½ D A2 = ½ m ω02 Α2 = ½ m 4π2 f02 Α2
Kmax = ½ m υ02 = ½ m ωδ2 Α2 = ½ m 4π2 fδ2 Α2 = 4 Umax
Umax = Κmax => f0 = fδ
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
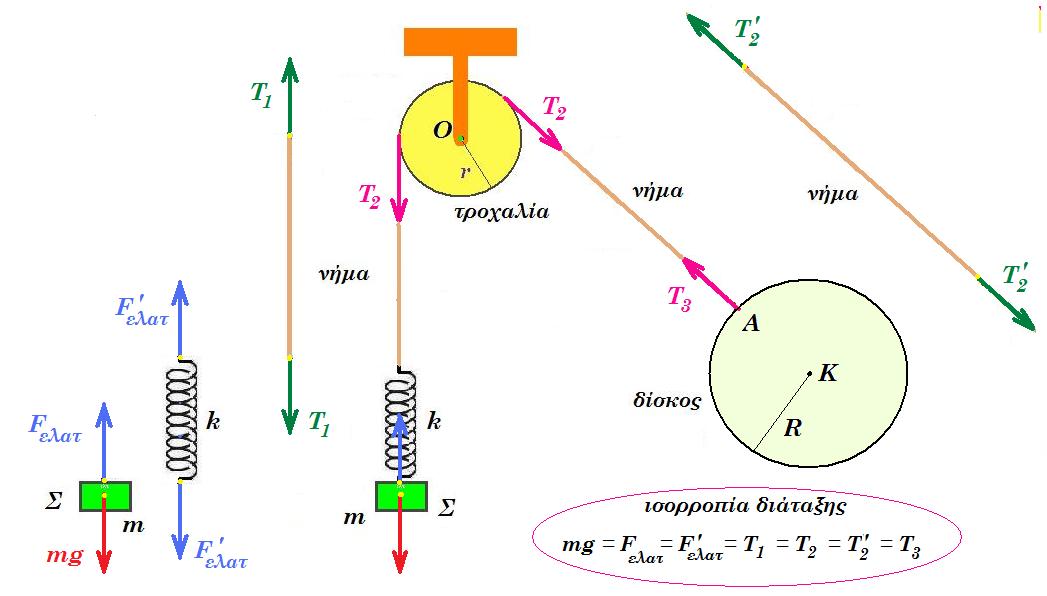
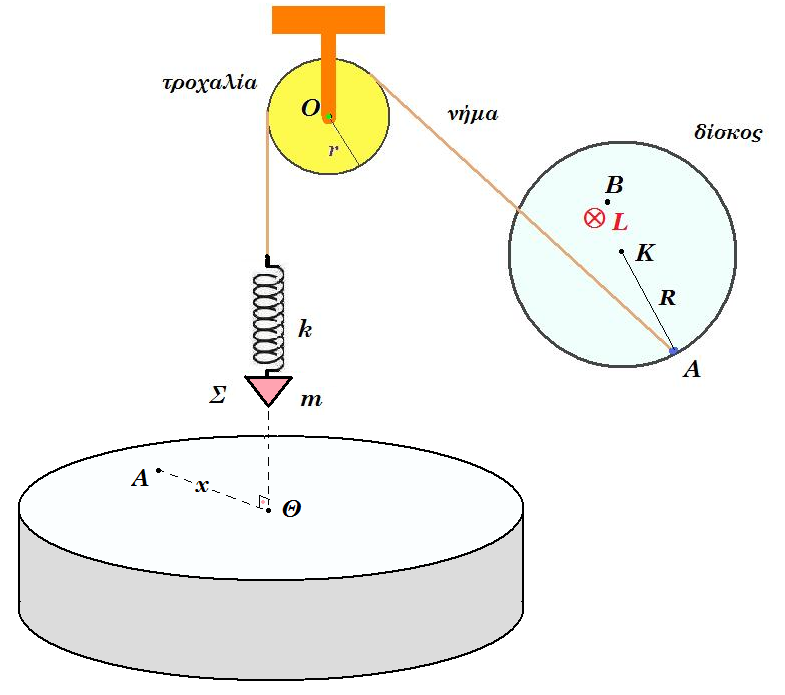
Στην κατακόρυφη διάταξη του σχήματος ο δίσκος ακτίνας R=0,5m περιστρέφεται γύρω από οριζόντιο άξονα χ'χ που διέρχεται από το κέντρο του Κ και είναι κάθετος στο επίπεδό του. Στοιχειώδης μάζα Δm του δίσκου που βρίσκεται στο σημείο Β (ΚΒ=0,2m) έχει κινητική ενέργεια 2.10-5J και στροφορμή μέτρου 4.10-6 kg m2/s. Το σώμα Σ μάζας m=1kg στο κάτω άκρο του ελατηρίου σταθεράς k=400N/m ταλαντώνεται εξ' αιτίας της περιστροφής του δίκου. Η τροχαλία έχει μηδαμινή μάζα, ακτίνα r=0,3m. Το νήμα μπορεί να ολισθαίνει στην περιφέρεια της τροχαλίας χωρίς τριβές.
(α) Βρείτε την επιτάχυνση του σημείου Α της περιφέρειας του δίσκου που συνδέεται μέσω αβαρούς νήματος με το σύστημα << ελατήριο - σώμα Σ >>.
(β) Για ποιά συχνότητα περιστροφής του δίσκου το σώμα ταλαντώνεται με μέγιστο πλάτος;
(γ) Βρείτε την εξίσωση της στροφορμής του σώματος Σ συναρτήσει του χρόνου.
(δ) Το κάτω άκρο του σώματος Σ, καθώς αυτό ταλαντώνεται, ακουμπά στο σημείο Θ της επιφάνειας υγρού με συνέπεια να δημιουργούνται εγκάρσια κύματα στην επιφάνεια του υγρού. Η ταχύτητα διάδοσης των κυμάτων στην επιφάνεια του υγρού είναι υ=2 m/s. Έστω σημείο Α της επιφάνειας του υγρού το οποίο απέχει απόσταση x=0,5m από το σημείο Θ.
(δ1) Βρείτε την εξίσωση της απομάκρυνσης του σημείου Α συναρτήσει του χρόνου.
(δ2) Βρείτε την διαφορά φάσης των ταλαντώσεων των σημείων Θ και Α.
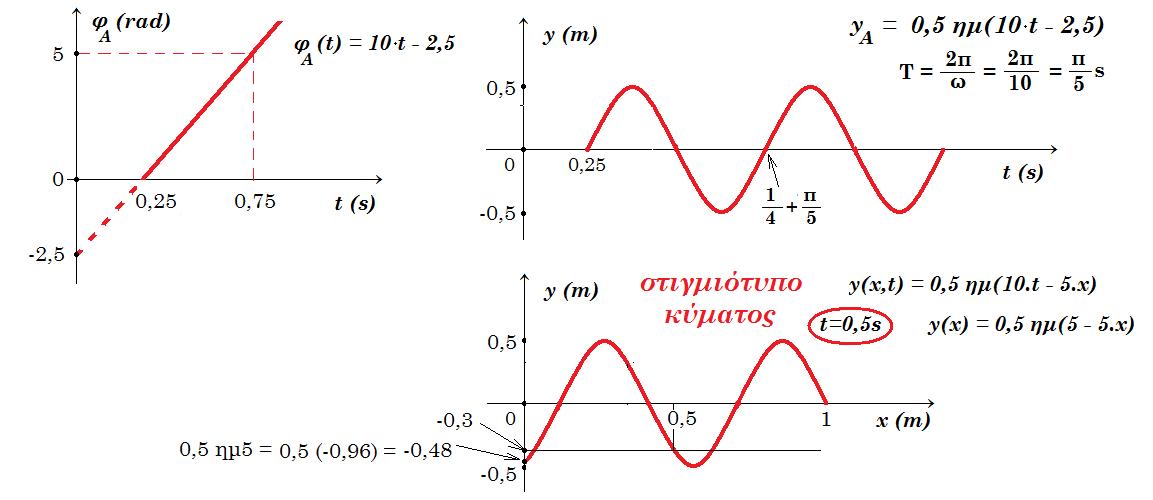
(δ3) Σχεδιάστε τη γραφική παράσταση της φάσης του σημείου Α συναρτήσει του χρόνου t.
(δ4) Σχεδιάστε τη γραφική παράσταση της απομάκρυνσης y συναρτήσει της απόστασης x τη στιγμή t=0,5s.
(A)
Κ = ½ Δm υ2 => 2 10-5 = ½ 10-5 υ2 => v2 = 4 => v = 2 m/s
L = Δm v (KB) = 10-5 2 0,2 = 4 10-6 kg m2/s
K / L = v / 2(KB) = ωδ / 2 => 2 10-5 / 4 10-6 = ωδ / 2 => ωδ = 10 rad/s συχνότητα διεγέρτη ( του δίσκου που περιστρέφεται )
v / 0,4 => v = 2 m/s Δm=10-5kg
ωδ = v / (KB) = 2 / 0,2 => ωδ = 10 rad/s
το σημείο Α στην περιφέρεια του δίσκου έχει κεντρομόλο επιτάχυνση λόγω περιστροφής ;
αΚ = ωδ2 (ΚΑ) = 100 rad2/s2 0,5 m = 50 m/s2
(B)
αμείωτη απλή αρμονική ταλάντωση ω02 = k/m = 400 / 1 => ω0 = 20 rad/s
για να έχουμε μέγιστο πλάτος ταλάντωσης του Σ ( συντονισμός ) πρέπει ωδ = ω0
(Γ)
ταλάντωση σώματος Σ : x(t) = 0,5 ημ(10 t + φ) v(t) = 5 συν(10 t + φ) α(t) = - 50 ημ(10 t + φ)
L = m r v = 1 kg 0,3 m 5 συν(10 t + φ) m/s = 1,5 συν(10 t + φ) kg.m2/s
(Δ)
yΘ = A ημ(2πt/T) => yΘ(t) = 0,5 ημ(10.t)
υ = λ / Τ = λ / (2π/ω) => λ = 2π υ / ω = 2π 2 m/s / 10 rad/s => λ = 0,4.π m
yΑ = A ημ(2πt/T - 2π.xA/λ) = 0,5 ημ(10.t - 2π.0,5/0,4.π) => yΑ(t) = 0,5 ημ(10.t - 2,5)
Δφ = φΘ - φΑ = 10.t - (10.t - 2,5) = 2,5 rad
η φάση του σημείου Α είναι εξίσωση ευθείας με κλίση α = 10 rad/s
y = A ημ(2πt/T - 2π.x/λ) = 0,5 ημ(10.t - 2π.x/0,4.π) => y(x,t) = 0,5 ημ(10.t - 5.x)
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Στην επιφάνεια ενός υγρού που ηρεμεί, βρίσκονται δύο σύγχρονες σημειακές πηγές Π1 και Π2, που δημιουργούν στην επιφάνεια του υγρού εγκάρσια αρμονικά κύματα ίσου πλάτους. Οι πηγές αρχίζουν να ταλαντώνονται τη χρονική στιγμή t0=0 ξεκινώντας από τη θέση ισορροπίας τους και κινούμενες προς την ίδια κατεύθυνση, την οποία θεωρούμε θετική. Η χρονική εξίσωση της ταλάντωσης ενός σημείου Μ, που βρίσκεται στη μεσοκάθετο του ευθύγραμμου τμήματος Π1Π2, μετά τη συμβολή των κυμάτων δίνεται στο SI από τη σχέση: yM = 0,2 ημ2π(5t-10).
Η ταχύτητα διάδοσης των κυμάτων στην επιφάνεια του υγρού είναι υ=2 m/s. Έστω Ο το μέσο του ευθύγραμμου τμήματος Π1Π2 και d=1m η απόσταση μεταξύ των πηγών.
Να βρείτε:
Γ1. Την απόσταση ΜΠ1.
Γ2. Τη διαφορά φάσης των ταλαντώσεων των σημείων Ο και Μ.
Γ3. Πόσα σημεία του ευθύγραμμου τμήματος Π1Π2 ταλαντώνονται με μέγιστο πλάτος.
Γ4. Να σχεδιάσετε τη γραφική παράσταση της απομάκρυνσης του σημείου Μ σε συνάρτηση με τον χρόνο t για 0 ≤ t ≤ 2,5s.
y1 = A ημ(2πt/T - 2πx1/λ) y2 = A ημ(2πt/T - 2πx2/λ)
yM = y1 + y2 = 2A συν(πx2/λ - πx1/λ) ημ( 2πt/T - 2π (x1 + x2) / 2λ )
yM = 0,2 ημ2π(5t-10) => 1/Τ = 5 => Τ = 0,2s λ = υ Τ = 2 0,2 = 0,4 m
(x1 + x2) / 2λ = 10 => (x1 + x2) = 20 λ = 20 v T = 20 2 0,2 = 8m
επειδή το Μ είναι στην μεσοκάθετο x1 = x2 = 4 m
2A = 0,2 m => A = 0,1 m
yO = y1 + y2 = 2A συν(πx2/λ - πx1/λ) ημ( 2πt/T - 2π (x1 + x2) / 2λ ) =
= 2 0,1 συν(0) ημ( 2πt/0,2 - 2π (x1 + x2) / 2λ ) = 0,2 ημ( 10πt - 2π 1 / 2 0,4 ) =
yO = 0,2 ημ2π(5t - 1,25)
φΟ - φΜ = 2π(5t - 1,25) - 2π(5t - 10) = 20π - 2,5π = 17,5π
συν(πx2/λ - πx1/λ) = 1 ή -1 => χ2 - χ1 = Ν λ
χ1 + χ2 = Π1Π2 = 1 m => 2 χ2 = Ν 0,4 + 1 => χ2 = 0,2 Ν + 0,5
πρέπει 0 < χ2 < 1 m =>
=> 0 < 0,2 Ν + 0,5 < 1 m => - 0,5 < 0,2 Ν < 0,5 => - 2,5 < Ν < 2,5 =>
Ν = -2, -1, 0, 1, 2
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
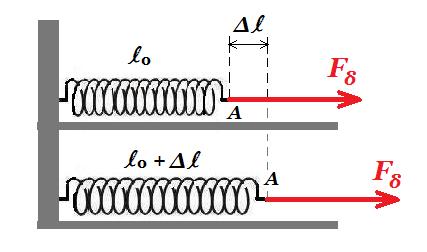 Σώμα μάζας 2kg ταλαντώνεται σε λείο οριζόντιο επίπεδο, δεμένο στο άκρο ιδανικού ελατηρίου σταθεράς k=40Ν/m, με την επίδραση εξωτερικής δύναμης της μορφής Fδ=F0∙ημ(5t+θ), με σταθερό πλάτος Α=0,5m, ενώ δέχεται δύναμη απόσβεσης της μορφής Fαπόσβ.=-b∙υ, .
Σώμα μάζας 2kg ταλαντώνεται σε λείο οριζόντιο επίπεδο, δεμένο στο άκρο ιδανικού ελατηρίου σταθεράς k=40Ν/m, με την επίδραση εξωτερικής δύναμης της μορφής Fδ=F0∙ημ(5t+θ), με σταθερό πλάτος Α=0,5m, ενώ δέχεται δύναμη απόσβεσης της μορφής Fαπόσβ.=-b∙υ, .
- Να βρεθεί η δύναμη του διεγέρτη τη στιγμή t0 που το σώμα βρίσκεται στην θέση x=+Α.
- Αν τη στιγμή t1 που το σώμα περνά από την θέση x=0 η δύναμη του διεγέρτη έχει μέτρο 1Ν, να υπολογιστεί η σταθερά απόσβεσης b.
- Σε μια άλλη στιγμή t2, το σώμα έχει ταχύτητα υ2=+2m/s. Να βρεθεί η ισχύς της δύναμης του διεγέρτη την στιγμή αυτή.
(1) αμείωτη απλή αρμονική ταλάντωση ω02 = k/m = 40 / 2 => ω0 = √20 rad/s
η συχνότητα του διεγέρτη είναι ωδ = 5 rad/s > ω0 = √20 rad/s δεν έχουμε συντονισμό
το σώμα ταλαντώνεται με την συχνότητα του διεγέρτη ωδ = 5 rad/s
στο σώμα ενεργούν στον άξονα χ'χ οι δυνάμεις : ελατηρίου, απόσβεσης, διεγέρτη
ΣF = m a => Fδ - b v - k x = m a => F0∙ημ(5t + θ) - b v - k x = m a (1)
όταν το σώμα είναι στη θέση x = +Α έχουμε α = - ω2 Α < 0 & η ταχύτητα είναι μηδέν
η (1) => Fδ - b v - k x = m a => Fδ - 0 - 40 N/m (+ 0,5 m) = 2 kg (- 52 rad2/s2 0,5 m ) => Fδ = - 5 N
F0∙ημ(5.t0 + θ) = - 5 N => F0 = 5 N και ημ(5.t0 + θ) = - 1 => 5.t0 + θ = 3π/2 + 2Νπ Ν = 0, 1, ... (1)
η απομάκρυνση x(t) = 0,5 ημ(5.t + φ)
τότε x(t0) = 0,5 ημ(5.t0 + φ) = + 0,5 => ημ(5.t0 + φ) = +1 => 5.t0 + φ = π/2 + 2Νπ Ν = 0, 1, ... (2)
από (1) - (2) => θ = π + φ
(2) όταν τη στιγμή t1 το σώμα περνά από τη θέση x = 0 έχουμε α = 0 η εξωτερική δύναμη έχει μέτρο 1 Ν και η ταχύτητα είναι μέγιστη υmax = ω Α = 5 rad/s 0,5 m = 2,5 m/s
η (1) => 1 N - b 2,5 m/s = 0 => b = 1/2,5 = 0,4 kg/s
x(t1) = 0,5 ημ(5.t1 + φ) = 0 => ημ(5.t1 + φ) = 0 => 5.t1 + φ = Νπ Ν = 0, 1, ...
τότε ημ(5.t1 + θ) = ημ(5.t1 + π + φ) = ημ(5.t1 + φ + π) = - ημ(5.t1 + φ) = 0 ;;;;;;;;
x(t) = 0,5 ημ(5.t + φ) v(t) = 2,5 συν(5.t + φ) α(t) = - 12,5 ημ(5.t + φ)
v(t2) = 2,5 συν(5.t2 + φ) = + 2 m/s => συν(5.t2 + φ) = +0,8 οπότε ημ(5.t2 + φ) = ± 0,6
F0∙ημ(5t + θ) - b v - k x = m a => F0/m ημ(5t + θ) = x'' + b/m x' + k/m x
5∙ημ(5t + θ) - 0,4 2,5 συν(5.t + φ) - 40 0,5 ημ(5.t + φ) = 2 [ - 12,5 ημ(5.t + φ) ]
5∙ημ(5t + θ) - συν(5.t + φ) - 20 ημ(5.t + φ) = - 25 ημ(5.t + φ)
5∙ημ(5t + θ) = συν(5.t + φ) - 5 ημ(5.t + φ)
 Σώμα μάζας 2kg ταλαντώνεται σε λείο οριζόντιο επίπεδο, δεμένο στο άκρο ιδανικού ελατηρίου σταθεράς k=40Ν/m, με την επίδραση εξωτερικής δύναμης της μορφής Fδ=F0∙ημ(5t+θ), με σταθερό πλάτος Α=0,5m, ενώ δέχεται δύναμη απόσβεσης της μορφής Fαπόσβ.=-b∙υ, .
Σώμα μάζας 2kg ταλαντώνεται σε λείο οριζόντιο επίπεδο, δεμένο στο άκρο ιδανικού ελατηρίου σταθεράς k=40Ν/m, με την επίδραση εξωτερικής δύναμης της μορφής Fδ=F0∙ημ(5t+θ), με σταθερό πλάτος Α=0,5m, ενώ δέχεται δύναμη απόσβεσης της μορφής Fαπόσβ.=-b∙υ, .



