σχήμα (α)

Στο σχήμα (α) φαίνεται μια ομογενής, λεπτή και ισοπαχής ράβδος μήκους ℓ = 1,2 m, μάζας Μ και βάρους 30 Ν.  Το άκρο Α της ράβδου είναι δεμένο σε αβαρές κατακόρυφο νήμα, το άλλο άκρο του οποίου είναι ακλόνητα στερεωμένο.  Η ράβδος βρίσκεται σε επαφή με στήριγμα στο σημείο Γ, το οποίο απέχει από το άκρο Α απόσταση 𝛢𝛤 = 2ℓ/3.  Η ράβδος ισορροπεί σε οριζόντια θέση.  Η ροπή αδράνειας της ράβδου ως προς κατακόρυφο άξονα, ο οποίος περνά από το σημείο Γ και είναι κάθετος στη ράβδο δίνεται από τη σχέση  𝐼 = 1/9 𝑀ℓ².  

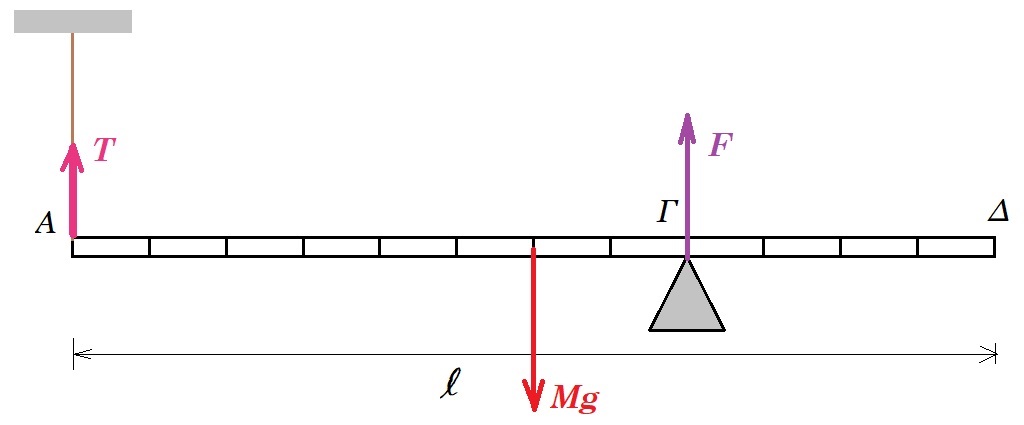
(α)  Να μεταφέρετε το σχήμα στο τετράδιο απαντήσεων και να σχεδιάσετε όλες τις δυνάμεις που ασκούνται στη ράβδο.
(β)  Να υπολογίσετε το μέτρο της τάσης που ασκεί το νήμα στη ράβδο.
(γ)  Να προσδιορίσετε το μέτρο και την κατεύθυνση της δύναμης που δέχεται το στήριγμα από τη ράβδο.
(δ)  Κόβουμε από τη ράβδο τμήμα μήκους ℓ/6 και το τοποθετούμε πάνω στη ράβδο, όπως φαίνεται στο σχήμα (β).  Να αναφέρετε αν θα αλλάξει η δύναμη που δέχεται το στήριγμα από τη ράβδο, που υπολογίσατε στο ερώτημα (β).

σχήμα (β)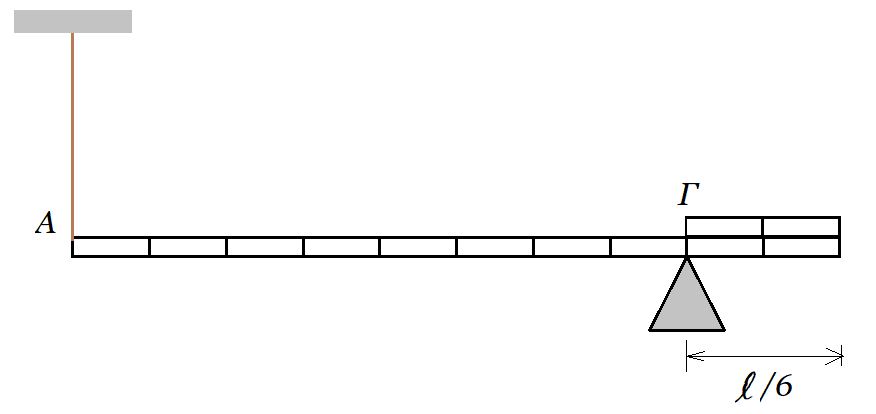

ισορροπία ράβδου :   ΣF_y = 0  =>  T  +  F  -  Mg  =  0     

                                Στ_(Α)  =  0  =>  F  2l/3  -  Mg  l/2  =  0  =>    F  2/3  =  30  1/2  =  0  =>   F  =  22,5 N 

                                Στ_(Γ)  =  0  =>   Mg  l/6   -  Τ  2l/3  =  0  =>    Τ  2/3  =  30  1/6  =  0  =>   Τ  =  7,5 N 

το στήριγμα στο σημείο Γ δέχεται από την ράβδο  δύναμη αντίθετη της  F 

ισορροπία ράβδου :   ΣF_y = 0  =>  T'  +  F'  -  (m₁ + m₂) g  =  0          m₁ = 8/12 M = 2M/3       m₂ = M/3

Στ_(Α)  =  0  =>  F'  2l/3  -  m₁ g 4l/12  -  m₁ g  9l/12 =  0  =>  F'  8/12  =  20  4/12  +  10  9/12 =  0  =>  F' = 170/8 N 

Στ_(Γ)  =  0  =>  -  Τ'  2l/3  +  m₁ g 4l/12  -  m₁ g  l/12 =  0  =>  Τ'  8/12  =  20  4/12  -  10  1/12 =  0  =>  Τ' = 70/8 N

~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~