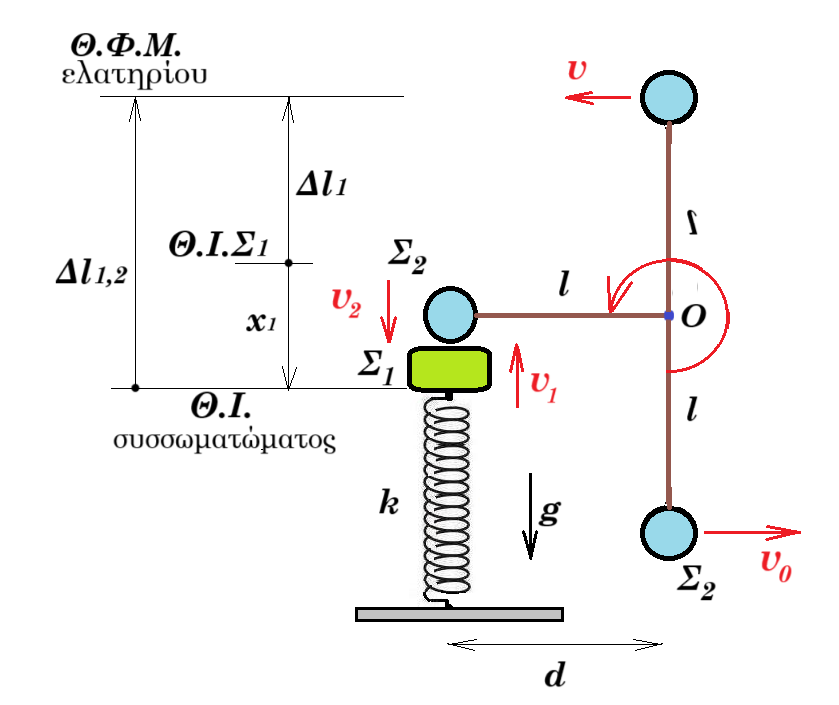
Σώμα Σ₁ μάζας m₁ = 1 kg εκτελεί απλή αρμονική ταλάντωση κατακόρυφης διεύθυνσης πλάτους Α και σταθεράς επαναφοράς D = k δεμένο στο πάνω άκρο κατακόρυφου ιδανικού ελατηρίου σταθεράς k το κάτω άκρο του οποίου είναι στερεωμένο σε σημείο οριζόντιου επιπέδου. Σώμα Σ₂ μάζας m₂ = 1 kg που ισορροπεί ακίνητο είναι δεμένο στο κάτω άκρο αβαρούς και μη εκτατού κατακόρυφου νήματος μήκους ℓ το άλλο άκρο του οποίου είναι ακλόνητα στερεωμένο σε σημείο Ο. Κάποια χρονική στιγμή προσδίδουμε οριζόντια ταχύτητα μέτρου υ₀ στο Σ₂ με φορά προς τα δεξιά με αποτέλεσμα το Σ₂ να εκτελέσει οριακά ανακύκλωση. Το υψηλότερο σημείο της τροχιάς του σώματος Σ₂ ανήκει στο ίδιο οριζόντιο επίπεδο με την θέση φυσικού μήκους του ελατηρίου. Η απόσταση του άξονα του ελατηρίου και του νήματος όταν το τελευταίο έχει κατακόρυφη διεύθυνση είναι d = 0,4 m. Τα δύο σώματα συγκρούονται πλαστικά με αποτέλεσμα το συσσωμάτωμα που δημιουργείται να παραμένει ακίνητο μετά την κρούση. Θεωρήστε τα σώματα σημειακά και τις αντιστάσεις από τον αέρα αμελητέες.
Δίνεται g = 10 m/s². Να υπολογίσετε :
1) το μήκος ℓ του νήματος.
2) το μέτρο της ταχύτητας υ₀ του σώματος Σ₂.
3) τη σταθερά k του ελατηρίου.
4) την ενέργεια της κατακόρυφης ταλάντωσης που εκτελούσε το σώμα Σ₁ πριν την κρούση με το σώμα Σ₂.

οριακά περνά από την ανώτερη θέση : η τάση του νήματος είναι μηδέν το βάρος είναι η κεντρομόλος δύναμη : mg = m v2 / l => v2 = g l
διατήρηση ενέργειας από τν κατώτερη θέση έως την ανώτερη θέση : ½ m v02 = ½ m v2 + mg 2l => v02 = gl + 4gl = 5gl
πλαστική κρούση : m1 v1 + m2 v2 = (m1 + m2) 0 = 0 v1 = - v2 για να παραμένει ακίνητο το συσσωμάτωμα πρέπει οι ταχύτητες πριν την κρούση να είναι αντίθετες διότι οι μάζες είναι ίσες και η κρούση γίνεται στη θέση ισορροπίας του συσσωματώματος αλλιώς θα έκανε ταλάντωση
αυτό σημαίνει ότι η ταχύτητα του Σ2 είναι κατακόρυφη προς τα κάτω
Δl1,2 = l = d = 0,4 m
θέση ισορροπίας Σ1 : m1 g = k Δl1 = 10 N
θέση ισορροπίας Σ1+Σ2 : (m1 + m2) g = k Δl1,2 => 20 N = k 0,4 m => k = 50 N/m
άρα Δl1 = 10 / 50 = 0,2 m κα x1 = Δl1,2 - Δl1 = 0,4 - 0,2 = 0,2 m
η κρούση γίνεται πάνω στην κατακόρυφο του άξονα του ελατηρίου όταν το νήμα γίνεται οριζόντιο συνεπως l = d = 0,4 m άρα v02 = 5 g l = 5 10 0,4 = 20 => v0 = 20½ m/s
½ m v02 = ½ m v22 + mg l => v02 = v22 + 2 g l =>
5gl = v22 + 2 g l => v22 = 3gl = 3 10 0,4 = 12 => v2 = 12½ m/s άρα v1 = 12½ m/s
E = 0,5 m v12 + 0,5 k x12 = 0,5 k A2 => E = ½ 1 12 + ½ 50 0,22 = 6 + 1 = 7 J
!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!
ισορροπία Γ : mg + mg = T1 ισορροπία Β : Τ1 + mg = k1 Δl 3mg = k1 Δl
ισορροπία Ε : mg + 3mg = T2 ισορροπία Δ : Τ2 + mg = k2 Δl 5mg = k2 Δl k1 / k2 = 3/5 = 0,6
ισορροπία Γ + Β : 2mg = k1 χ1 πλάτος Α1 = Δl - χ1 = (3mg - 2mg) / k1 = mg / k1
k1 = 2m ω2 = 2m 4π2/Τ12 => Τ12 = 4π2 2m/k1
ισορροπία Ε + Δ : 4mg = k2 χ2 πλάτος Α2 = Δl - χ2 = (5mg - 4mg) / k2 = mg / k2 A1 / A2 = 5/3
k2 = 2m ω2 = 4m 4π2/Τ22 => Τ22 = 4π2 4m/k2 T1/T2 = (5/6)½ < 1
Γ : T1 - mg = - m 4π2/Τ12 Α1 = - m k1/2m mg/k1 = - mg/2 => T1 = mg/2
ισορροπία Β : Τ1 + mg = k1 Δl

Στο σχήμα βλέπετε τέσσερα σώματα Β, Γ, Δ και Ε, τα οποία ηρεμούν στο κάτω άκρο δύο ιδανικών ελατηρίων με σταθερές k1 και k2, τα οποία έχουν το ίδιο φυσικό μήκος l0. Τα σώματα έχουν μάζες mΒ=mΓ=mΔ=m και mΕ=3m, ενώ με την άσκηση κατακόρυφης δύναμης μέτρου F=mg στα σώματα Γ και Ε, τα ελατήρια έχουν το ίδιο μήκος. Κάποια στιγμή καταργώντας την δύναμη F τα δυο συστήματα σωμάτων (Β-Γ και Δ-Ε) εκτελούν αατ.
i) Οι σταθερές των δύο ελατηρίων συνδέονται με την σχέση:
α) k1/k2=0,4, β) k1/k2=0,5, γ) k1/k2=0,6.
ii) Για τα πλάτη των δύο ταλαντώσεων ισχύει:
α) Α1 < Α2, β) Α1 = Α2, γ) Α1 > Α2.
iii) Για τις περιόδους των δύο ταλαντώσεων ισχύει:
α) Τ1 < Τ2, β) Τ1 = Τ2, γ) Τ1 > Τ2.
iv) Να εξετάσετε αν, κατά τη διάρκεια των ταλαντώσεων, κάποιο από τα νήματα που συνδέει τα σώματα Β-Γ και Δ-Ε χαλαρώσει.
Δύναμη Lorentz σε ταλάντωση
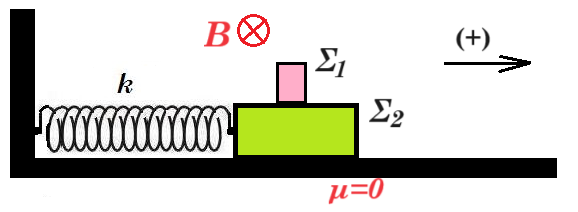
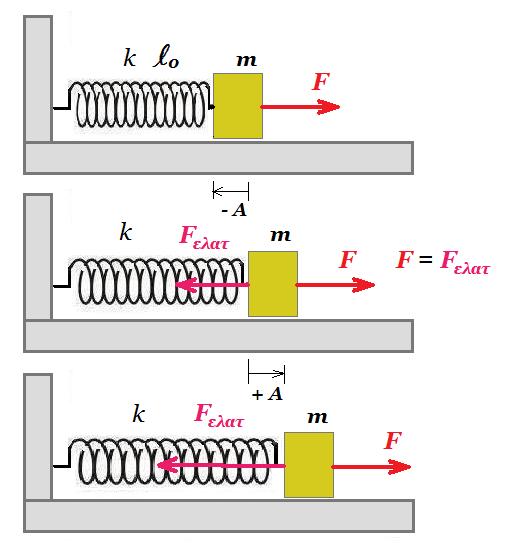
Το σύστημα των δύο σωμάτων Σ1 και Σ2 του σχήματος εκτελεί απλή αρμονική ταλάντωση χωρίς το σώμα Σ1 να ολισθαίνει πάνω στο Σ2 με εξίσωση x = 0,2ημ(ωt) (SI). Το οριζόντιο δάπεδο είναι λείο. Το ελατήριο είναι ιδανικό με σταθερά k = 8 N/m. Το σώμα Σ2 έχει μάζα Μ = 1,995 kg και είναι δεμένο στο δεξί άκρο του ελατηρίου. Το σώμα Σ1 είναι από μονωτικό υλικό έχει μάζα m = 5∙10–3 kg και φέρει φορτίο q = 0,1 C. Στο χώρο επικρατεί οριζόντιο μαγνητικό πεδίο έντασης Β = 1 Τ και φοράς από τον αναγνώστη προς τη σελίδα κάθετη στη διεύθυνση της ταλάντωσης. Δίνεται g = 10 m/s2 και ότι οι αντιστάσεις του αέρα είναι αμελητέες
α. της στιγμή που το σύστημα (Σ1 – Σ2) θα βρεθεί πρώτη φορά στη θέση x1 = 0,12 m:
i. Να βρεθεί η στατική τριβή που δέχεται το σώμα Σ1 από το σώμα Σ2
ii. Να βρεθεί η δύναμη που δέχεται το Σ1 από το μαγνητικό πεδίο
β. Να βρεθεί η μέγιστη τιμή της κάθετης συνιστώσας της δύναμης επαφής που δέχεται το σώμα Σ1 από το σώμα Σ2 και η χρονική στιγμή που πρώτη φορά επιτυγχάνεται.
Λ Υ Σ Η
k = (M+m) ω2 => 8 = 2 ω2 => ω = 2 rad/s Τ = 2π/ω = 2π/2 = π sec
x = 0,2 ημ(2t) (S.I.) υ = 0,4 συν(2t) α = - 0,8 ημ(2t) t = 0 x = 0 υ = 0,4 m/s α = 0
Σ1 , Σ2 : ΣF = (M+m) α => Fελατ = - k x = (M+m) α => - 8 0,2 ημ(2t) = 2 { - 0,8 ημ(2t) } ο.ε.δ.
Σ2 : ΣF = M α => Fελατ - T = - k x - Τ = Μ α
το Σ1 μετατοπίζεται δεξιά με ταχύτητα προς τα δεξιά τότε η δύναμη τριβής Τ είναι προς τα αριστερά και η δύναμη Lorentz είναι προς τα πάνω :
ΣFx = m α => τριβή T = m α = 0,005 { - 0,8 ημ(2t) } = - 0,004 ημ(2t)
ΣFy = 0 => FL + N - mg = 0 => N = mg - qυΒ => N = 0,05 - 0,1 0,4 συν(2t) => N = 0,05 - 0,04 συν(2t)
Nmax = 0,09 N όταν συν(2t) = -1 = συν(π) => 2t = (2κ+1)π κ = 0, 1, 2, 3, ... => t = (2κ+1)π/2 sec
x = 0,12 m = 0,2 ημ(2t) => ημ(2t) = 0,6 τότε συν(2t) = 0,8 τότε υ = 0,4 συν(2t) = 0,4 0,8 = 0,32 m/s τότε FL = qυΒ = 0,1 0,32 1 = 0,032 N και Ν = 0,05 - 0,04 0,8 = 0,018 Ν και |Τ| = 0,004 0,6 = 0,0024 Ν
ρυθμός μεταβολής Κ για το Σ1 :
dK/dt = m υ α = 0,005 0,4 συν(2t) { - 0,8 ημ(2t) } = - 0,0016 ημ(2t) συν(2t) = - 0,0008 ημ(4t)
ρυθμός μεταβολής Κ για το Σ2 :
dK/dt = Μ υ α = 1,995 0,4 συν(2t) { - 0,8 ημ(2t) } = - 0,6384 ημ(2t) συν(2t) = - 0,3192 ημ(4t)
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
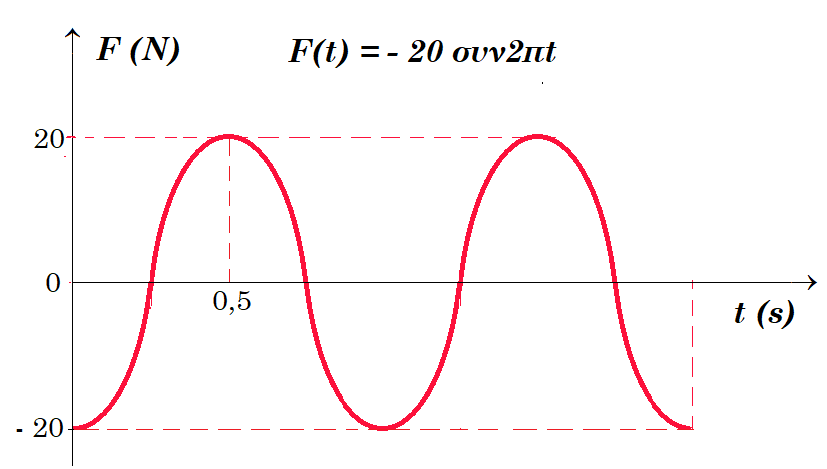
Ένα σώμα μάζας 1kg εκτελεί απλή αρμονική ταλάντωση, με την επίδραση δύναμης επαναφοράς, η οποία μεταβάλλεται με το χρόνο, όπως στο διπλανό σχήμα. Να βρεθούν:
α. Το πλάτος και η ορμή του σώματος την στιγμή t1=0,25s.
β. Η εξίσωση της απομάκρυνσης σε συνάρτηση με το χρόνο (x=f(t)).
γ. Το έργο της δύναμης επαναφοράς από τη στιγμή t1=0,25s έως την στιγμή t2=0,5s.
δ. Να γίνει η γραφική παράσταση της δυναμι
κής ενέργειας ταλάντωσης σε συνάρτηση με το χρόνο και να υπολογισθεί ο ρυθμός μεταβολής της (της δυναμικής ενέργειας) την στιγμή t2.
Δίνεται π2 ≈10
Τ = 1 s , f = 1 Hz , ω = 2π / Τ = 2π rad/s , F(t) = - 20 συν2πt a = F / m = - 20 συν2πt
v = - 20/2π ημ2πt = - 10/π ημ2πt = - π ημ2πt x = π/2π συν2πt = 0,5 συν2πt = 0,5 ημ(2πt + π/2)
t = 0,25 s v = - π ημ(2π 0,25) = - π ημ(π/2) = - π m/s A = 0,5 m
t = 0,5 s v = - π ημ(2π 0,5) = - π ημ(π) = 0
K0,5s - K0,25s = 0 - 0,5 1 kg (- π m/s)2 = - 0,5 π2 = - 5 J = WF
PF = F v = - 20 συν2πt ( - π ημ2πt ) = 20π ημ2πt συν2πt = 10π ημ4πt
WF = W0 - 10π/4π συν4πt => WF(t) = W0 - 2,5 συν4πt
W(0) = 0 => W0 - 2,5 συν4πt = 0 => W0 = 2,5 J άρα WF(t) = 2,5 - 2,5 συν4πt
WF = 2,5 - 2,5 συν(4π 0,5) - [ 2,5 - 2,5 συν(4π 0,25) ] = - 2,5 συν2π + 2,5 συνπ = - 2,5 + 2,5 (-1) = - 5 J
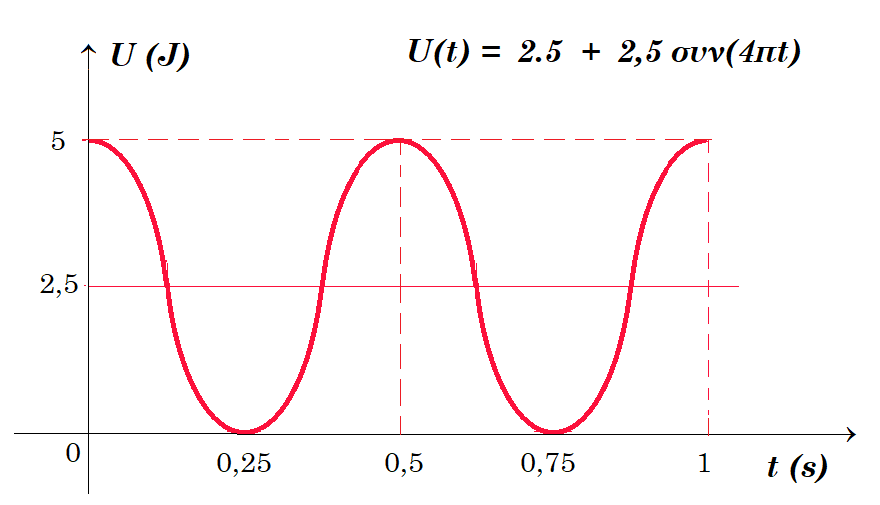
U = 0,5 D x2 = 0,5 m ω2 x2 = 0,5 1 4π2 0,25 συν22πt => U(t) = 5 συν2(2πt)
U(t) = 5 συν2(2πt) = 5 ( 1 + συν(4πt) ) / 2 = 2.5 + 2,5 συν(4πt)
dU/dt = 10 συν(2πt) 2π ( - ημ(2πt) ) = - 20π ημ2πt συν2πt = - 10π ημ4πt
t = 0,5 s dU/dt = - 10π ημ(4π 0,5) = 0
ΑΣΚΗΣΗ 1
| Σώμα μάζας m = 3 kg εκτελεί ΑΑΤ, στο σχήμα φαίνεται το διάγραμμα υ(t) της ταχύτητας συναρτήσει του χρόνου, εκφράστε τις εξισώσεις x(t), υ(t), a(t) : απομάκρυνσης, ταχύτητας και επιτάχυνσης συναρτήσει το χρόνου, καθώς και της δυναμικής U(t) και κινητικής K(t) ενέργειας ως προς τον χρόνο |
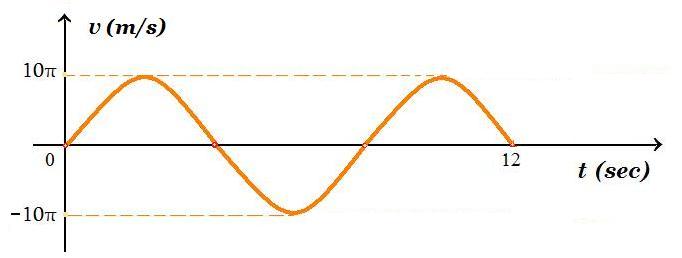 |
12 sec = 3Τ/2 => Τ = 8 sec τότε ω = 2π/Τ = 2π/8 => ω = π/4 rad/s κυκλική συχνότητα ταλάντωσης
η εξίσωση της ταχύτητας συναρτήσει του χρόνου : υ = 10π ημ(π/4.t)
υmax = ω . Α => 10π = π/4 . Α => Α = 40 m το πλάτος της Απλής Αρμονικής Ταλάντωσης
η εξίσωση της επιτάχυνσης συναρτήσει του χρόνου : α = dυ/dt = 10π.π/4 συν(π/4.t) => a = 5π2/2 συν(π/4.t)
επειδή α = - ω2.x τότε η εξίσωση της απομάκρυνσης συναρτήσει του χρόνου : x = - 40 συν(π/4.t)
x = 40 ημ(π/4.t + 3π/2) υ = dx/dt = 10π συν(π/4.t + 3π/2) α = dυ/dt = - 5π2/2 ημ(π/4.t + 3π/2)
δυναμική ενέργεια : U = ½ D x2 = ½ m ω2 x2 = ½ 3 (π/4)2 402 ημ2(π/4.t + 3π/2) => U(t) = 150 π2 ημ2(π/4.t + 3π/2)
κινητική ενέργεια : K = ½ m υ2 = ½ 3 100 π2 συν2(π/4.t + 3π/2) => K(t) = 150 π2 συν2(π/4.t + 3π/2)

ΑΣΚΗΣΗ 2
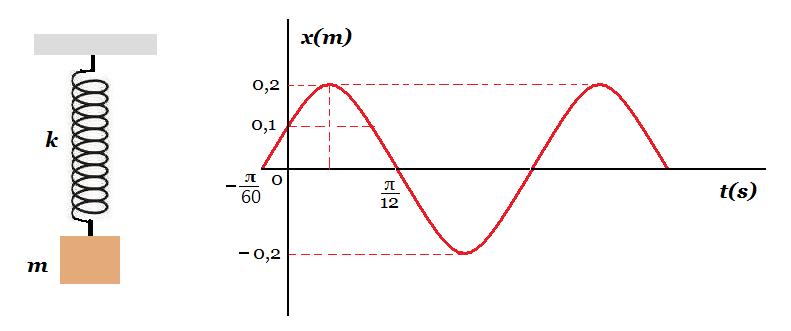
Σώμα μάζας m = 2 kg είναι δεμένο στο κάτω άκρο κατακόρυφου ελατηρίου και ισορροπεί όπως στο σχήμα. Απομακρύνουμε το σώμα από τη θέση ισορροπίας κατά x1 = 0,1 m κατακόρυφα προς τα πάνω, δίνουμε ταχύτητα υ0 στο σώμα και το αφήνουμε να ταλαντωθεί. Η γραφική παράσταση της απομάκρυνσης συναρτήσει του χρόνου φαίνεται στο σχήμα. Θεωρούμε θετική φορά προς τα πάνω.
(A) Να βρεθεί η ταχύτητα υ0 , η συχνότητα της ταλάντωσης και η επιμήκυνση του ελατηρίου στην ισορροπία του σώματος.
(B) Ποιες χρονικές στιγμές η απομάκρυνση είναι : (α) + 0,1 m (β) + 0,2 m (γ) - 0,1 m;
(Γ) Ποια είναι η ταχύτητα του σώματος τη στιγμή που η δύναμη επαναφοράς έχει μέτρο 24 Ν;
(Α) το πλάτος της ταλάντωσης, από το σχήμα, είναι Α = 0,2 m και για t = 0 x = + 0,1 m έχουμε :
0 < x < 0,1 => 0 < 0,2 ημ2πt/Τ < 0,1 => 0 < ημ2πt/Τ < ½ => ημ0 < ημ2πt/Τ < ημπ/6 => 0 < 2πt/Τ < π/6 =>
=> 0 < t < Τ/12 Δt1 = T/12
0,1 < x < 0,2 => 0,1 < 0,2 ημ2πt/Τ < 0,2 => ½ < ημ2πt/Τ < 1 => ημπ/6 < ημ2πt/Τ < ημπ/2 => π/6 < 2πt/Τ < π/2
=> Τ/12 < t < Τ/4 Δt2 = T/4 - T/12 = T/6 = 2.Δt1
π/12 = Τ/6 + Τ/6 + Τ/12 = 5Τ/12 => Τ = π/5 sec η περίοδος της ταλάντωσης του σώματος
τότε f = 1/T = 5/π Hz συχνότητα της ταλάντωσης του σώματος
ω = 2π/Τ = 2π f = 2π.5/π => ω = 10 rad/sec κυκλική συχνότητα της ταλάντωσης του σώματος
από τη θεωρία x = A ημ(ωt + θ) => 0,1 = 0,2 ημθ => ημθ = ½ => θ = π/6 ή 5π/6 επειδή όμως το σώμα απομακρύνεται η ταχύτητα υ0 είναι θετική άρα θ = π/6 διότι συν(5π/6) = - 0,866 = - √3/2 < 0
άρα απομάκρυνση x(t) = 0,2.ημ(10t + π/6) (1) ταχύτητα υ(t) = 2.συν(10t + π/6) (2)
επιτάχυνση α(t) = - 20.ημ(10t + π/6) (3) δύναμη επαναφοράς F(t) = m.a(t) = - 40.ημ(10t + π/6) (4)
k = m . ω2 = 2 . 102 = 200 N/m σταθερά ελατηρίου
ΣF = m.a => Fελατ - m.g = m.a => Fελατ = m.g + ( - m.ω2.x ) => Fελατηρίου (t) = k.[ Δl - x(t) ]
δύναμη ελατηρίου Fελατηρίου (t) = k.[ Δl - x(t) ] = 200.[ 0,1 - 0,2.ημ(10t + π/6) ] = 20 - 40.ημ(10t + π/6) ] (5) για τη δύναμη ελατηρίου μετράμε από το φυσικό του μήκος
στην ισορροπία έχουμε : m g = k Δl => 2 . 10 = 200 . Δl => Δl = 0,1 m επιμήκυνση του ελατηρίου στην ισορροπία συνεπώς όταν απομακρύνουμε το σώμα από τη Θ.Ι. κατά 0,1 m και του δίνουμε ταχύτητα υ0 το ελατήριο έχει το φυσικό του μήκος και το σώμα ξεκινά την ταλάντωση του
διατήρηση ενέργειας : ½.m.υ02 + ½.k.x12 = ½.k.A2 => 2 . υ02 + 200 . 0,12 = 200 . 0,22 => υ02= 100 . (0,04 - 0,01) = 3 => υ0 = +√3 m/s
άλλος τρόπος : η (2) => υ(t) = 2 συν(10.t + π/6) => υ(0) = 2 συν(π/6) = 2.(+√3/2) = +√3 m/s
(Β) x(t) = 0,2.ημ(10t + π/6) = +0,1 => ημ(10t + π/6) = +½ = ημ(π/6) = ημ(5π/6) =>
=> 10t + π/6 = 2Νπ + π/6 ή 10t + π/6 = 2Νπ + 5π/6
10t + π/6 = 2Νπ + π/6 => 10t = 2Νπ => t = Νπ/5 Ν = 0, 1, 2, 3, ... t = 0, π/5 s, 2π/5 s, 3π/5 s, ...
ή 10t + π/6 = 2Νπ + 5π/6 => 10t = 2Νπ + 4.π/6 = 2Νπ + 2π/3 => t = Ν.π/5 + π/15
Ν = 0, 1, 2, 3, ... t = π/15 s, (π/5 + π/15) s, (2π/5 + π/15) s
x(t) = 0,2.ημ(10t + π/6) = +0,2 => ημ(10t + π/6) = +1 = ημ(π/2) => 10t + π/6 = 2Νπ + π/2 =>
=> 10t = 2Νπ + π/2 - π/6 = 2Νπ + π/3 => t = Νπ/5 + π/30
Ν = 0, 1, 2, 3, ... t = π/30 s, t = π/5 + π/30 s, t = 2.π/5 + π/30 s
x(t) = 0,2 ημ(10t + π/6) = - 0,1 => ημ(10t + π/6) = - ½ = ημ( 11π/6 ) =>
=> 10t + π/6 = 2Νπ + 7π/6 ή 10t + π/6 = 2Νπ + 11π/6
10t + π/6 = 2Νπ + 7π/6 => 10t = 2Νπ + π => t = Νπ/5 + π/10
Ν = 0, 1, 2, ... t = π/10 , π/5 + π/10 , 2π/5 + π/10 , ....
ή 10t + π/6 = 2Νπ + 11π/6 => 10t = 2Νπ + 5π/3 => t = Νπ/5 + π/6
Ν = 0, 1, 2, .... t = π/6 , π/5 + π/6 , 2π/5 + π/6 , ...
(Γ) F(t) = - 40.ημ(10t + π/6) => 24 = - 40.ημ(10t + π/6) => ημ(10t + π/6) = - 0,6 => συν(10t + π/6) = ± 0,8 τότε ταχύτητα υ = 2.(±0,8) = ±1,6 m/s
ΑΣΚΗΣΗ 3
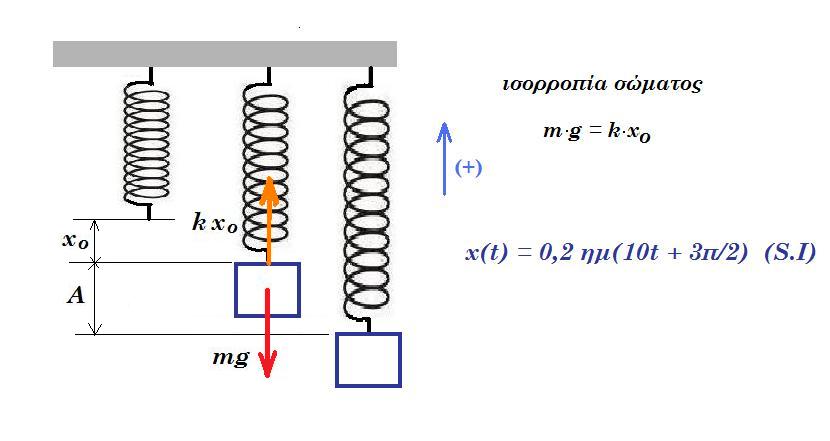
Tο σώμα του σχήματος μάζας m = 1 Kg είναι δεμένο στο κατακόρυφο ελατήριο σταθεράς Κ = 100 Ν/m και πραγματοποιεί απλή αρμονική ταλάντωση ενώ η απομάκρυνσή του από τη θέση ισορροπίας περιγράφεται από τη χρονική εξίσωση : x(t) = 0,2.ημ(10t + 3π/2) (S.I).
Εκφράστε την δυναμική ενέργεια του ελατηρίου σε συνάρτηση με το χρόνο t και σε συνάρτηση με την απομάκρυνση x από τη θέση ισορροπίας του σώματος.
Α = 0,2 m ω = 10 rad/s Τ = 2π/ω = 2π/10 = π/5 sec f = 5/π Hz x(t) = 0,2.ημ(10t + 3π/2)
υ(t) = 2.συν(10t + 3π/2) α(t) = -20.ημ(10t + 3π/2)
ισορροπία σώματος : m.g = k.x0 => x0 = 1.10 / 100 = 0,1 m
U(t) = ½.k.x(t)2 = ½. 100 . 0,22.ημ2(10t + 3π/2) = 2.ημ2(10t + 3π/2)
Umax = ½.k.A2 = ½. 100 . 0,22 = 2 Joule
U(x) = ½.k.x2 = 50.x2
ΣF = - D . x => - m.g + Fελατ = - k . x(t) => Fελατ = m.g - k . x(t) m.g = k.x0
Fελατ(t) = k. ( x0 - x(t) ) = k.x0 - k.x(t) = 10 - 20.ημ(10t + 3π/2) Fελατ(0) = 10 - (-20) = + 30 N
Uελατ(t) = ½.k. { x0 - x(t) }2 = 50. { 0,1 - 0,2.ημ(10t + 3π/2) }2 =
= 50. { 0,01 + 0,04.ημ2(10t + 3π/2) - 0,04.ημ(10t + 3π/2) } =
= 0,5 + 2.ημ2(10t + 3π/2) - 2.ημ(10t + 3π/2) = 0,5 + 1 - συν(20t + 3π) - 2.ημ(10t + 3π/2) =
= 1,5 - συν(20t + π) - 2.ημ(10t + 3π/2)
Uελατ(x) = ½.k. ( x0 - x )2 = 50. ( 0,1 - x )2 όπου - 0,2 m < x < + 0,2 m
όταν το σώμα βρίσκεται στην κατώτατη θέση ταλάντωσης ( x = - 0,2 m ) : Uελατ(-0,2) = 50. ( 0,1 - x )2 = 50. ( 0,1 - (-0,2) )2 = 50 . ( 0,3 )2 = 4,5 J το ελατήριο είναι επιμηκυμένο κατά το μέγιστο 0,3 m
όταν το σώμα βρίσκεται στην ανώτατη θέση ταλάντωσης ( x = + 0,2 m ) : Uελατ(+0,2) = 50. ( 0,1 - x )2 = 50. ( 0,1 - 0,2 )2 = 50 . ( - 0,1 )2 = 0,5 J το ελατήριο είναι συσπειρωμένο κατά το μέγιστο 0,1 m
όταν το σώμα περνά από τη θέση ισορροπίας x = 0 Uελατ(0) = 50. ( 0,1 - x )2 = 50. ( 0,1)2 = 0,5 J το ελατήριο είναι επιμηκυμένο 0,1 m
ΑΣΚΗΣΗ 4
Ένα κατακόρυφο ιδανικό ελατήριο σταθεράς k = 200 N/m έχει το πάνω άκρο του στερεωμένο σε μια οροφή. Στο κάτω άκρο του ελατηρίου έχει προσδεθεί σώμα μάζας m = 2 kg που ισορροπεί. Μετακινούμε το σώμα προς τα πάνω κατά Δl = 0,2 m και τη χρονική στιγμή t0 = 0 το αφήνουμε ελεύθερο. Το σώμα ξεκινά να εκτελεί απλή αρμονική ταλάντωση. Θεωρώντας θετική την κατακόρυφη προς τα κάτω φορά να βρείτε:
α) την αρχική φάση φ0 της ταλάντωσης.
β) τη μέγιστη ταχύτητα υmax του σώματος κατά τη διάρκεια της ταλάντωσης.
γ) την κινητική ενέργεια Κ του σώματος τις χρονικές στιγμές που η δυναμική ενέργεια ταλάντωσης είναι U=1J .
δ) το μέτρο της μέγιστης δύναμης Fελατ,max που ασκεί το ελατήριο στο σώμα κατά τη διάρκεια της ταλάντωσης.
Δίνεται: g = 10 m/s2.
(α) η θετική κατεύθυνση είναι κατακόρυφη προς τα κάτω, μετακινούμε το σώμα προς τα πάνω και το αφήνουμε ελεύθερο να ταλαντωθεί, άρα τη στιγμή 0 είναι σε απομάκρυνση x(0) = - A = - 0,2 m = - Δl, συνεπώς η αρχική φάση φ0 της ταλάντωσης είναι φ0 = 3π/2 x(t) = 0,2 . ημ(ωt + 3π/2)
(β) k = m . ω2 => 200 = 2 . ω2 => ω = 10 rad/s vmax = ω . A = 10 . 0,2 = 2 m/s
x(t) = 0,2 . ημ(ω.t + 3π/2) => x(t) = 0,2 . ημ(10.t + 3π/2) υ(t) = 2 . συν(10.t + 3π/2)
α(t) = - 20 . ημ(10.t + 3π/2) F(t) = - 40 . ημ(10.t + 3π/2)
(γ) U = ½ . k . x2 => 1 J = 1/2 . 200 N/m . x2 => x = ± 0,1 m
Ε = ½ . k . Α2 = ½ . 200 . 0,22 = ½ . 200 . 0,04 = 4 J E = K + U => K = E - U = 4 J - 1 J = 3 J
(δ) η θέση ισορροπίας του σώματος m . g = k . d => d = 2 . 10 / 200 = 0,1 m
τη στιγμή μηδέν που το σώμα ξεκινά την ταλάντωση το ελατήριο είναι συσπειρωμένο κατά
Α - d = 0,2 - 01 = 0,1 m = x0 αρχική συσπείρωση ελατηρίου
ΣF = - D . x => m.g + Fελατ = - k . x(t) => Fελατ = - m.g - k . x(t) m.g = k.d στην ισορροπία
η δύναμη που ασκεί το ελατήριο στο σώμα κατά τη διάρκεια της ταλάντωσης :
Fελατ(t) = k . { - d - x(t) } = 200 . { - 0,1 - 0,2 . ημ(10.t + 3π/2) } => Fελατ(t) = - 20 - 40 ημ(10.t + 3π/2)
t = 0 (στην άνω ακραία θέση) : Fελατ(0) = - 20 - 40 . ημ(3π/2) = - 20 - 40.(-1) = + 20 N συσπείρωση 0,1 m
Τ = 2π/ω = 2π/10 = π/5 sec
t = T/2 (στην κάτω ακραία θέση) : επιμήκυνση 0,3 m
Fελατ(T/2) = - 20 - 40 ημ(2π/Τ . Τ/2 + 3π/2) = - 20 - 40 ημ(π + 3π/2) = - 20 - 40.(+1) = - 60 N = Fελατ,max
t = T/4 (όταν διέρχεται από τη Θ.Ι.) : επιμήκυνση 0,1 m
Fελατ(T/4) = - 20 - 40 ημ(2π/Τ .Τ/4 + 3π/2) = - 20 - 40 ημ(π/2 + 3π/2) = - 20 - 40 ημ(2π) = - 20 - 40 . 0 = - 20 N

ΑΣΚΗΣΗ 5
Στο σχήμα φαίνεται το διάγραμμα επιτάχυνσης – χρόνου για ένα σώμα που εκτελεί απλή αρμονική ταλάντωση. Το μέτρο της μεταβολής της αλγεβρικής τιμής της ορμής ανάμεσα σε δύο διαδοχικές διελεύσεις του σώματος από τη θέση ισορροπίας είναι Δp = 2π kg.m/s . Να βρεθούν:
Α. η αρχική φάση της ταλάντωσης.
B. το πλάτος της ταλάντωσης.
Γ. η μάζα του σώματος.
Δ. ο ρυθμός μεταβολής της ορμής του σώματος τη χρονική στιγμή t1 που η επιτάχυνση είναι 25 m/s2. Δίνεται π2 = 10 
3.T/4 = 0,3 s => Τ = 0,4 sec => ω = 2π / Τ = 2π / 0,4 = 5π rad/s
α((t) = 50 . συν5.t = 50 . ημ(5.t + π/2) = - 50 . ημ(5π.t + 3π/2) = α((t)
υ((t) = 10/π . συν(5π.t + 3π/2) x((t) = 2/π2 . ημ(5π.t + 3π/2) = 0,2 . ημ(5π.t + 3π/2)
Δp = 2π kgm/s => 2 .m .vmax = 2.π => m .ω Α = π => m . 5.π . 0,2 = π => m = 1 kg
dp / dt = F = m . a = 1 . 25 = 25 kg.m/s2 = 25 Ν
ΑΣΚΗΣΗ 6
Ένα σώμα μάζας m = 2 kg ισορροπεί δεμένο στο πάνω άκρο κατακόρυφου ιδανικού ελατηρίου σταθεράς k = 50 N/m, του οποίου το κάτω άκρο είναι στερεωμένο στο δάπεδο. Εκτρέπουμε κατακόρυφα το σώμα προς τα πάνω μέχρι το φυσικό μήκος του ελατηρίου και το αφήνουμε ελεύθερο. Να βρεθούν:
(Α) το πλάτος της ταλάντωσης του σώματος.
(Β) η ενέργεια που δαπανήθηκε για να εκτρέψουμε το σώμα από τη θέση ισορροπίας του μέχρι τη θέση του φυσικού μήκους του ελατηρίου.
(Γ) η μέγιστη δυναμική ενέργεια της ταλάντωσης και η μέγιστη δυναμική ενέργεια του ελατηρίου κατά τη διάρκεια της ταλάντωσης.
(Δ) η χρονική στιγμή κατά την οποία το σώμα θα αποκτήσει ταχύτητα μέτρου υ = √3 m/s για δεύτερη φορά.
Θεωρείστε θετική φορά προς τα πάνω. Δίνεται : g = 10 m/s2.
k = m . ω2 => 50 = 2 . ω2 => ω = 5 rad/s Τ = 2π/ω = 2π/5 s f = 1/T = 5/2π Hz
(Α) στη θέση ισορροπίας το ελατήριο είναι συσπειρωμένο κατά d ισχύει :
m . g = k . d => d = m.g / k = 2 . 10 / 50 => d = 0,4 m
το πλάτος της ταλάντωσης είναι Α = d = 0,4 m
(Β) Uελατ + W = Uβαρυτ => ½.k.d2 + W = m.g.d => ½ . 50 . 0,42 + W = 2 .10 .0,4 => W = 8 - 4 = 4 J
(Γ) x((t) = 0,4 . ημ(5.t + π/2) υ((t) = 2 . συν(5.t + π/2) α((t) = - 10 . ημ(5.t + π/2)
F(t) = m . a(t) = - 20 . ημ(5.t + π/2)
U(t) = ½ . k . x(t)2 = ½ . 50 . 0,42 . ημ2(5.t + π/2) = 4 . ημ2(5.t + π/2) Umax = 4 J μέγιστη δυναμική ενέργεια της ταλάντωσης του σώματος
η δύναμη που ασκεί το ελατήριο στο σώμα κατά τη διάρκεια της ταλάντωσης :
ΣF = - D . x = m a => - m.g + Fελατ = - k . x(t) => Fελατ = m.g - k . x(t) = m g + m a =>
=> Fελατ = k . d - k . x(t) = k . { d - x(t) } => Fελατ (t) = 50 . { 0,4 - 0,4.ημ(5.t + π/2) } =>
=> Fελατ(t) = 20 - 20 ημ(5.t + π/2) Fελατ(0) = 20 - 20 ημ(π/2) = 0 ( άνω ακραία θέση )
t = T/2 (στην κάτω ακραία θέση) :
Fελατ(T/2) = 20 - 20 ημ(2π/Τ .Τ/2 + π/2) = 20 - 20 ημ(3π/2) = 20 - 20 . (-1) = + 40 N = Fελατ,max
t = T/4 (όταν διέρχεται από τη Θ.Ι.) :
Fελατ(T/4) = 20 - 20 ημ(2π/Τ .Τ/4 + π/2) = 20 - 20 ημ(π/2 + π/2) = 20 - 20 ημ(π) = + 20 N
η μέγιστη συσπείρωση του ελατηρίου είναι 2.Α = 0,8 m τότε Fελατ,max = k.2.Α = 50.0,8 = 40Ν
και η δυναμική ενέργεια του ελατηρίου : Uελατ,max = ½ . k . (2.A)2 = ½ . 50 . (0,8)2 = 16 J
Uελατ(t) = ½ . k . { d - x(t) }2 = ½ . 50 . { 0,4 - 0,4 . ημ(5.t + π/2) }2 = ½ . 50 .0,4 . { 1 - ημ(5.t + π/2) }2 =
= 10 + 10 ημ2(5.t + π/2) - 20 ημ(5.t + π/2) } = 10 + 5 - 5 συν(10.t + π) - 20 ημ(5.t + π/2) }
τελικά : Uελατ(t) = 15 - 5 συν(10.t + π) - 20 ημ(5.t + π/2) }
Uελατ(x) = ½ . k . { d - x }2 = ½ . 50 . { 0,4 - x }2 όπου - 0,4 m < x < + 0,4 m
(Δ) υ((t) = 2 . συν(5.t + π/2) => + √3 = 2 . συν(5.t + π/2) =>
=> συν(5.t + π/2) = + √3/2 = συν(π/6) = συν(11π/6) τότε
5.t + π/2 = Ν.2π + π/6 Ν = 1, 2, 3, ... τότε 5.t = Ν.2π + π/6 - π/2 = Ν.2π - π/3 => t = Ν.2π/5 - π/15
N = 1 t = 2π/5 - π/15 = 6π/5 - π/15 = 5π/15 s 4η φορά το σώμα ανεβαίνει υ = +√3 m/s
N = 2 t = 4π/5 - π/15 = 12π/5 - π/15 = 11π/15 s 8η φορά το σώμα ανεβαίνει υ = +√3 m/s
ή 5.t + π/2 = Ν.2π + 11π/6 N = 0, 1, 2, ... τότε 5.t = Ν.2π + 11π/6 - π/2 = N.2π + 4π/3 => t = Ν.2π/5 + 4π/15
Ν = 0 t = 4π/15 s 3η φορά το σώμα ανεβαίνει υ = +√3 m/s
N = 1 t = 2π/5 + 4π/15 = 10π/15 s 7η φορά το σώμα ανεβαίνει υ = +√3 m/s
υ((t) = 2 συν(5.t + π/2) => - √3 = 2 συν(5.t + π/2) => συν(5.t + π/2) = -√3/2 = συν(5π/6) = συν(7π/6) =>
5.t + π/2 = Ν.2π + 5π/6 Ν = 0, 1, 2, ... 5.t = Ν.2π + 5π/6 - π/2 = Ν.2π + π/3 => t = Ν.2π/5 + π/15
N = 0 t = π/15 s 1η φορά το σώμα κατεβαίνει υ = -√3 m/s
N = 1 t = 2π/5 + π/15 = 7π/15 s 5η φορά το σώμα κατεβαίνει υ = -√3 m/s
ή 5.t + π/2 = Ν.2π + 7π/6 N = 0, 1, 2, ... 5.t = Ν.2π + 7π/6 - π/2 = N.2π + 2π/3 => t = Ν.2π/5 + 2π/15
Ν = 0 t = 2π/15 s 2η φορά το σώμα κατεβαίνει υ = -√3 m/s
N = 1 t = 2π/5 + 2π/15 = 8π/15 s 6η φορά το σώμα κατεβαίνει υ = -√3 m/s
ΑΣΚΗΣΗ 7
Ένα σώμα μάζας m εκτελεί απλή αρμονική ταλάντωση πλάτους A. Η ενέργεια της ταλάντωσης είναι E = 0,8 J. Η γραφική παράσταση της ταχύτητας υ του σώματος σε συνάρτηση με το χρόνο t απεικονίζεται στο παρακάτω σχήμα: 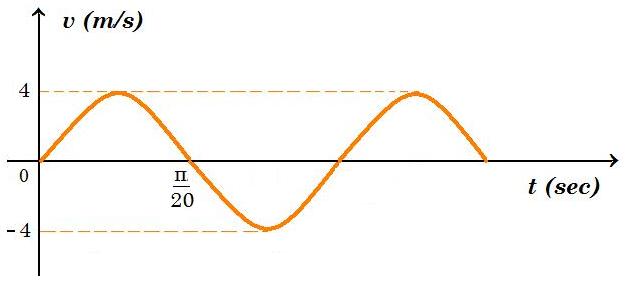 α) να βρείτε το πλάτος A της ταλάντωσης.
α) να βρείτε το πλάτος A της ταλάντωσης.
β) να υπολογίσετε τη σταθερά επαναφοράς D της ταλάντωσης.
γ) να παραστήσετε γραφικά τη φάση φ της ταλάντωσης συναρτήσει του χρόνου 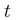 , στο χρονικό διάστημα από t0 = 0 ως t = T, αν γνωρίζουμε ότι η απομάκρυνση του σώματος μεταβάλλεται όπως το ημίτονο σε σχέση με το χρόνο.
, στο χρονικό διάστημα από t0 = 0 ως t = T, αν γνωρίζουμε ότι η απομάκρυνση του σώματος μεταβάλλεται όπως το ημίτονο σε σχέση με το χρόνο.
δ) να βρείτε το ρυθμό μεταβολής της ορμής του σώματος τη χρονική στιγμή t1 = π/40 s.
Τ = π/10 s ω = 2π/Τ = 20 rad/s από το διάγραμμα : υ(t) = 4 ημ20.t
η μέγιστη ταχύτητα 4 m/s E = Kmax = 1/2 m vmax2 => 0,8 J = 1/2 m (4 m/s)2 => m = 2 0,8 / 16 = 0,1 kg
x(t) = - 0,2 συν20.t = 0,2 ημ(20.t + 3π/2)
Α = 0,2 m D = m . ω2 υ(t) = 4 συν(20.t + 3π/2) α(t) = - 80 ημ(20.t + 3π/2)
από την ολική ενέργεια έχουμε E = 1/2 .D .A2 => 0,8 = 1/2 .D .0,22 => D = 40 N/m
m = D / ω2 = 40 / 400 = 0,1 kg
η φάση της ταλάντωσης : φ(t) = 20.t + 3π/2 t = 0 => φ(0) = 3π/2 rad
t = T = π/10 => φ(π/10) = 20. π/10 + 3π/2 = 2π + 3π/2 = 7π/2 rad
 Δp / Δt = F(t) = m . a(t) = 0,1 . [ - 80 . ημ(20.t + 3π/2) ] = - 8 . ημ(20.t + 3π/2)
Δp / Δt = F(t) = m . a(t) = 0,1 . [ - 80 . ημ(20.t + 3π/2) ] = - 8 . ημ(20.t + 3π/2)
F(π/40) = - 8 . ημ(20. π/40 + 3π/2) = - 0,8 . ημ(π/2+ 3π/2) = 0
πράγματι τη στιγμή π/40 s η ταχύτητα του σώματος είναι μέγιστη που σημαίνει ότι η ΣF = 0
ΑΣΚΗΣΗ 8
Κατακόρυφο ελατήριο σταθεράς k έχει το πάνω άκρο του στερεωμένο σε οροφή. Στο κάτω άκρο του ελατηρίου έχει προσδεθεί σώμα μάζας m που ισορροπεί. Στη θέση ισορροπίας το ελατήριο έχει επιμηκυνθεί κατά d = 0,1 m. Το σύστημα εκτελεί απλή αρμονική ταλάντωση με ενέργεια E = 2 J και η χρονική εξίσωση απομάκρυνσης είναι x(t) = 0,2 ημ(ωt + π) (SI). Θετική έχει θεωρηθεί η κατακόρυφη προς τα κάτω φορά. Να βρείτε:
(α) τη σταθερά k του ελατηρίου.
(β) τη μάζα m του σώματος.
(γ) τη γωνιακή συχνότητα ω της ταλάντωσης.
(δ) την ταχύτητα υ του σώματος, τη χρονική στιγμή t = π/30 s. Δίνεται : g = 10 m/s2.
(ε) να παραστήσετε γραφικά τη φάση φ της ταλάντωσης συναρτήσει του χρόνου t, στο χρονικό διάστημα από t0 = 0 ως t = T
ισορροπία σώματος m .g = k .d => k / m = g / d => ω2 = 10 / 0,1 = 100 => ω = 10 rad/s x(t) = 0,2. ημ(10.t + π) (SI)
Ε = ½.k.A2 => 2 = ½.k.0,22 => k = 4 / 0,04 = 100 N/m m = k / ω2 = 1kg
υ(t) = 2 συν(10.t + π) => υ(π/30) = 2 συν(10.π/30 + π) = 2 συν(π/3 + π) = 2.(-1/2) = -1 m/s
η φάση της ταλάντωσης : φ(t) = 10.t + π t = 0 => φ(0) = π rad
t = T = 2π/ω = 2π/10 s => φ(2π/10) = 10. 2π/10 + π = 2π + π = 3π rad
ΑΣΚΗΣΗ 9
Το σώμα Σ μάζας m = 1 kg του σχήματος είναι δεμένο στο ένα άκρο οριζοντίου ελατηρίου σταθεράς k = 400 N/m. Το άλλο άκρο του ελατηρίου είναι ακλόνητα στερεωμένο. Το σύστημα ελατήριο – σώμα Σ ισορροπεί σε λείο οριζόντιο επίπεδο. Τη χρονική στιγμή t0 = 0 ασκείται στο σώμα Σ σταθερή οριζόντια δύναμη μέτρου F με αποτέλεσμα το σύστημα να ξεκινήσει απλή αρμονική ταλάντωση πλάτους A = 0,4 m.
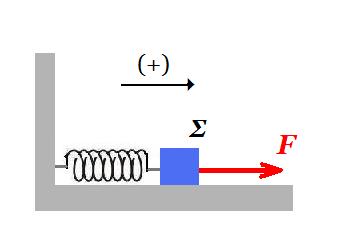 Να βρεθεί:α) το μέτρο F της δύναμης.β) η εξίσωση x = f(t) της απομάκρυνσης του σώματος από τη θέση ισορροπίας.γ) η εξίσωση Fελατ = f(t) της δύναμης που ασκεί το ελατήριο στο σώμα.δ) Το πλάτος Α' και η ολική ενέργεια Ε' της νέας ταλάντωσης που θα εκτελέσει το σώμα, αν κάποια στιγμή που το σώμα βρίσκεται στην ακραία θετική θέση ταλάντωσης, καταργηθεί η δύναμη F.
Να βρεθεί:α) το μέτρο F της δύναμης.β) η εξίσωση x = f(t) της απομάκρυνσης του σώματος από τη θέση ισορροπίας.γ) η εξίσωση Fελατ = f(t) της δύναμης που ασκεί το ελατήριο στο σώμα.δ) Το πλάτος Α' και η ολική ενέργεια Ε' της νέας ταλάντωσης που θα εκτελέσει το σώμα, αν κάποια στιγμή που το σώμα βρίσκεται στην ακραία θετική θέση ταλάντωσης, καταργηθεί η δύναμη F.
(Α) ω2 = k/m = 400 => ω = 20 rad/s
(Β) ΣF = F + Fελατ = F + k. Δx
στη Θέση Ισορροπίας της ταλάντωσης : ΣF = 0 => F - k.A = 0 => F = 400 . 0,4 = 160 N
τη στιγμή μηδέν το σώμα βρίσκεται στην θέση x = - A ως προς την ταλάντωση :
x(t) = Α . ημ(ωt + φ) = 0,4 . ημ(20.t + 3π/2) v(t) = 8 . συν(20.t + 3π/2)
(Γ) ΣF = - D . x => F + Fελατ = - k . x(t) =>
=> Fελατ = - F - k . x(t) => Fελατ = - 160 - 400 . 0,4 ημ(20.t + 3π/2) =>
=> Fελατ(t) = - 160 - 160 ημ(20.t + 3π/2)
(Δ) όταν F = 0 το σώμα βρίσκεται στην ακραία θετική θέση δηλαδή το ελατήριο έχει επιμήκυνση 0,8 m ενώ η νέα θέση ισορροπίας είναι η θέση φυσικού μήκους του ελατηρίου συνεπώς το νέο πλάτος ταλάντωσης του σώματος θα είναι : Α' = 0,8 m = 2.Α
Για τη νέα ολική ενέργεια της ταλάντωσης έχουμε : Ε' = ½ . k . (A')2 = ½ . 400 N/m . 0,82 m2 => E' = 128 J
WF = F A = 160 N 0,4 m = 64 J U = 0,5 k A2 = 0,5 400 0,42 = 200 0,16 = 32 J K = 0,5 m v2 = 0,5 1 82 = 32 J
WF = F 2A = 160 N 0,8 m = 128 J U = 0,5 k (2A)2 = 0,5 400 0,82 = 200 0,64 = 128 J K = 0 J
x(t) = +0,2m = 0,4 . ημ(20.t + 3π/2) => ημ(20.t + 3π/2) = +0,5 => συν2(20.t + 3π/2) = 3/4 v2 = 82 . συν2(20.t + 3π/2) = 64 3/4 = 48
WF = F = 160 N 0,6 m = 96 J U = 0,5 k x2 = 0,5 400 0,62 = 200 0,36 = 72 J K = 0,5 m v2 = 0,5 1 48 = 24 J
ΑΣΚΗΣΗ 10
|
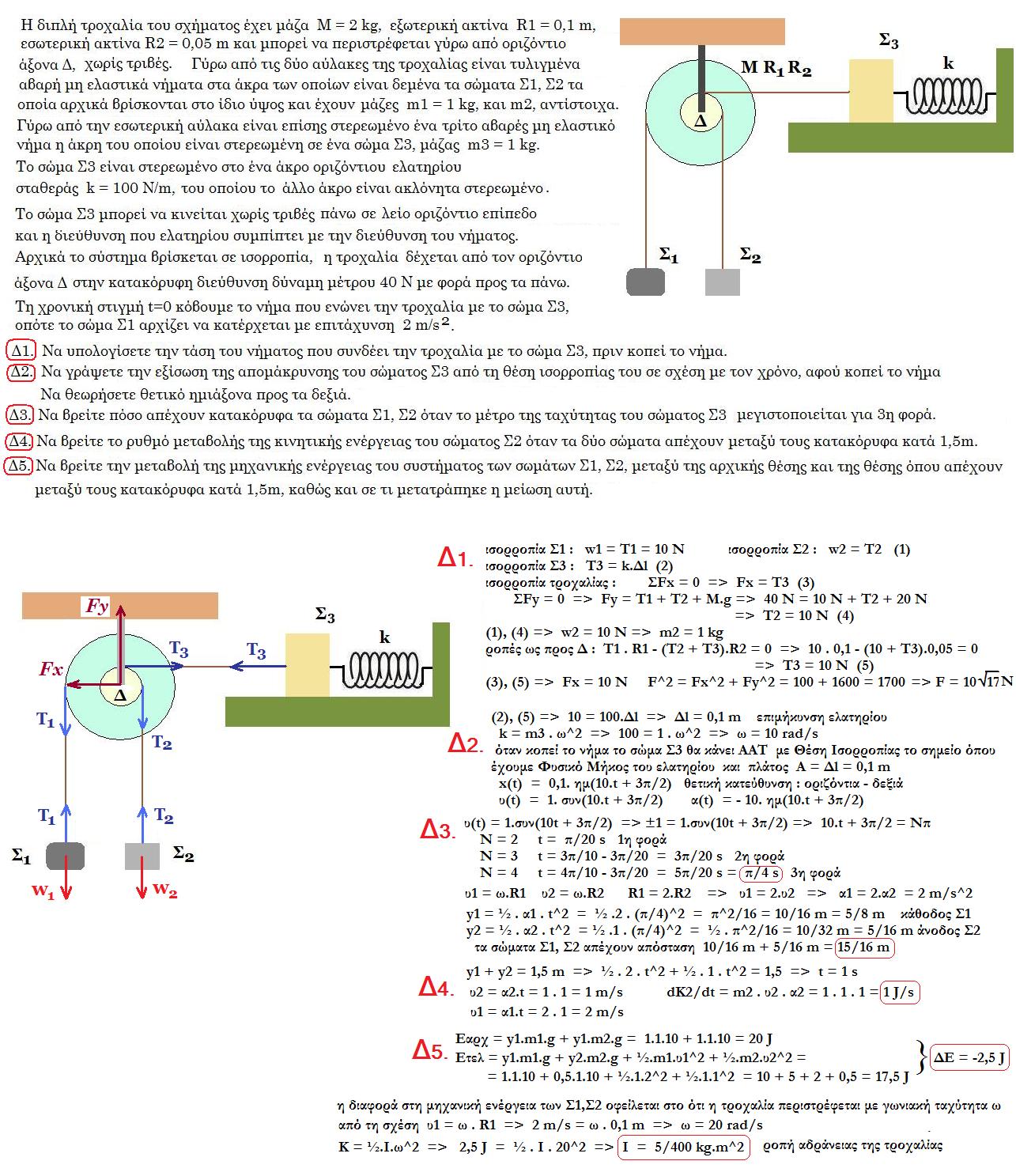
Στο σχήμα δείχνεται ένα κατακόρυφο ελατήριο σταθεράς k = 100 N/m στερεωμένο σε οροφή, στο κάτω άκρο του οποίου είναι στερεωμένο ένα σώμα Σ1, μάζας m1=1 kg. Από το σώμα Σ1 μέσω ενός μη εκτατού νήματος που έχει αμελητέα μάζα είναι κρεμασμένο ένα δεύτερο σώμα Σ2, μάζας m2 = 3 kg . Το σύστημα των σωμάτων αρχικά ισορροπεί.
Μετατοπίζουμε αργά το σώμα Σ2 προς τα κάτω κατά d = 0,4 m και το αφήνουμε ελεύθερο να κινηθεί τη χρονική στιγμή t0=0s. Το όλο σύστημα εκτελεί απλή αρμονική ταλάντωση με σταθερά επαναφοράς D=k χωρίς το νήμα να χαλαρώνει.
Γ1. Να υπολογίσετε την ενέργεια που δαπανήσαμε για να
θέσουμε το σύστημα σε ταλάντωση.
Γ2. Να γράψετε την εξίσωση της απομάκρυνσης του σώματος Σ2, γύρω από τη θέση ισορροπίας του, σε συνάρτηση του χρόνου.
Γ3. Να υπολογίσετε το ρυθμό μεταβολής της κινητικής ενέργειας του Σ2 τη χρονική στιγμή που η ταχύτητά του είναι υ1 = +1 m/s για δεύτερη φορά.
Γ4. Να υπολογίσετε το μέτρο της τάσης του νήματος τη χρονική στιγμή που η ταχύτητά του είναι υ1=+1m/s για δεύτερη φορά.
Γ5. Αν κόψουμε το νήμα τη χρονική στιγμή που το σώμα Σ2 βρίσκεται στην κατώτερη θέση της ταλάντωσής του, να βρείτε την μέγιστη ταχύτητα που αποκτά το σώμα Σ1.
Για την ταλάντωση θεωρούμε θετική την φορά προς τα πάνω. g = 10 m/s2
|
 |
ισορροπία σωμάτων ( m1 + m2 ) . g = k . x0 => ( 1 + 3 ) . 10 = 100 . x0 => x0 = 0,4 m αρχική επιμήκυνση του ελατηρίου
ΑΣΚΗΣΗ 11
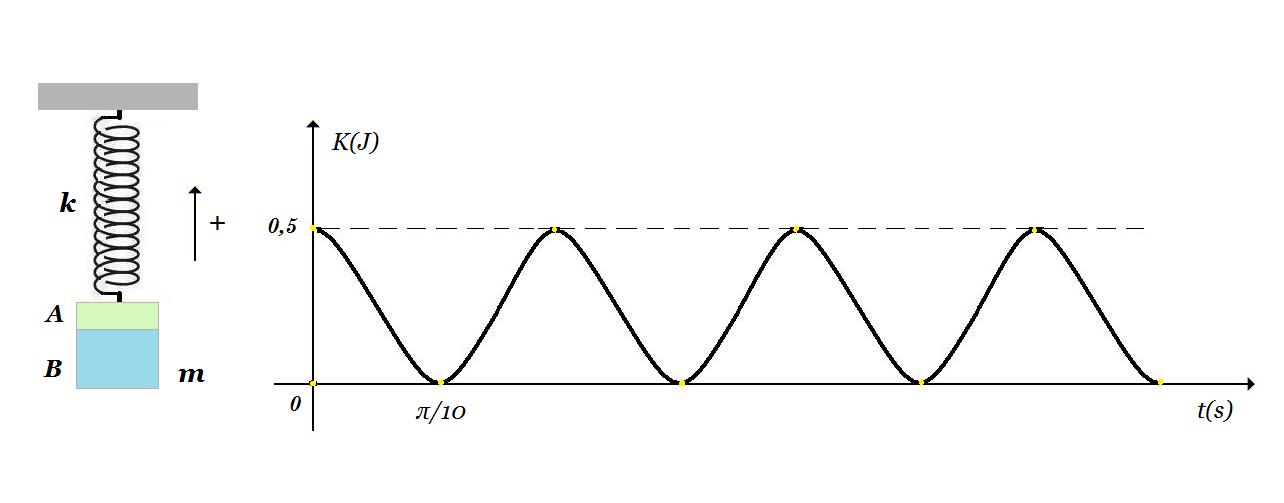
Σώμα Σ μάζας m = 4 kg προέκυψε από την συγκόλληση δύο σωμάτων Α και Β είναι δεμένο στο κάτω άκρο κατακόρυφου ιδανικού ελατηρίου σταθεράς k του οποίου το άλλο άκρο είναι ακλόνητα στερεωμένο στην οροφή. Το σώμα Σ εκτελεί απλή αρμονική ταλάντωση με σταθερά D=k. Στο σχήμα φαίνεται η γραφική παράστση της κινητικής ενέργειας του σώματος Σ συναρτήσει του χρόνου.
Γ1. Υπολογίστε το πλάτος και την περίοδο της ταλάντωσης του σώματος Σ.
Γ2. Γράψτε τη χρονική εξίσωση της απομάκρυνσης του σώματος Σ από τη θέση ισορροπίας αν είναι γνωστό ότι από τη στιγμή t = 0 έως τη στιγμή π/10 s η αλγεβρική τιμή της ταχύτητάς του είναι αρνητική.
Γ3. Βρείτε την αλγεβρική τιμή της ταχύτητας του σώματος Σ όταν η κινητική του ενέργεια ισούται με την δυναμική ενέργεια της ταλάντωσης για τρίτη φορά από τη στιγμή t = 0.
Γ4. Όταν το σώμα Σ βρίσκεται στην κατώτερη θέση της τροχιάς του το κομμάτι Β μάζας mΒ=3kg αποκολλάται ακαριαία και αρχίζει ελεύθερη πτώση. Το κομμάτι Α παραμένει δεμένο στο ελατήριο και συνεχίζει να εκτελεί απλή αρμονική ταλάντωση σταθεράς D = k. Υπολογίστε την τιμή του λόγου υmax / υ'max όπου υmax , υ'max οι μέγιστες τιμές της ταχύτητας των ταλαντώσεων του σώματων Σ και του κομματίου Α μετά την αποκόλληση, αντίστοιχα.
T/4 = π/10 s => Τ = 2π/5 s ω = 2π/Τ = 5 rad/s k = m ω2 = 4 52 = 100 N/m
Kmax = 0,5 k A2 => 0,5 J = 0,5 100 N/m A2 => A = 0,1 m
m g = k Δl => Δl = 4 10 / 100 = 0,4 m
x(t) = 0,1 ημ(5t + φ) v(t) = 0,5 συν(5t + φ) από 0 έως π/10 s η κινητική ενέργεια μειώνεται και η ταχύτητα είναι αρνητική συνεπώς το σώμα Σ οδεύει προς την ακραία θέση - Α = - 0,1 m δηλαδή φ = π rad
άρα x(t) = 0,1 ημ(5t + π) v(t) = 0,5 συν(5t + π) α(t) = - 2,5 ημ(5t + π)
F(t) = m a = 4 { - 2,5 ημ(5t + π) } => F(t) = - 10 ημ(5t + π) F(0) = - 10 ημ(π) = 0
ΣF = m a => Fελατ - m g = m a => Fελατ (t) = 40 - 10 ημ(5t + π) = 40 - 100 x(t)
Fελατ (0) = 40 - 10 ημ(π) = 40 - 100 x(0) = 40 Ν = m g = k Δl
Κ = U = E / 2 => 0,5 k x2 = 0,5 0,5 k A2 => x = ± A/√2 => 0,1 ημ(5t + π) = ± 0,1 / √2 =>
ημ(5t + π) = √2 / 2 = ημ(π/4) = ημ(3π/4)
5t + π = 2Νπ + π/4 => 5t = 2Νπ - 3π/4 => t = 2Νπ/5 - 3π/20 Ν = 1, 2, 3, ...
Ν = 1 t = 5π/20 s Ν = 2 t = 13π/20 s
ή 5t + π = 2Νπ + 3π/4 => 5t = 2Νπ - π/4 => t = 2Νπ/5 - π/20 Ν = 1, 2, 3, ...
Ν = 1 t = 7π/20 s Ν = 2 t = 15π/20 s
ημ(5t + π) = - √2 / 2 = ημ(5π/4) = ημ(7π/4)
5t + π = 2Νπ + 5π/4 => 5t = 2Νπ + π/4 => t = 2Νπ/5 + π/20 Ν = 0, 1, 2, ...
Ν = 0 t = π/20 s Ν = 1 t = 9π/20 s
ή 5t + π = 2Νπ + 7π/4 => 5t = 2Νπ + 3π/4 => t = 2Νπ/5 + 3π/20 Ν = 0, 1, 2, ...
Ν = 0 t = 3π/20 s Ν = 1 t = 11π/20 s
1η φορά Κ = U = E / 2 τη στιγμή t = π/20 s
2η φορά Κ = U = E / 2 τη στιγμή t = 3π/20 s
3η φορά Κ = U = E / 2 τη στιγμή t = 5π/20 s v(5π/20) = 0,5 συν(5 5π/20 + π) = 0,5 συν(π/4) = + 0,5 √2 / 2 = + √2 / 4 m/s
.............................................................................................................
όταν x = - A = - 0,1 m τότε υ = 0 το ελατήριο έχει επιμήκυνση 0,4 + 0,1 = 0,5 m , το κομμάτι Β αποκολλάται
Θ.Ι. για το Α : mA g = k xA => xA = 1 10 / 100 = 0,1 m
το Α θα κάνει Α.Α.Τ. με πλάτος 0,5 - 0,1 = 0,4 m ωΑ2 = k / mA = 100/1 = 100 => ωΑ=10rad/s
xA(t) = 0,4 ημ(10t + 3π/2) vA(t) = 4 συν(10t + 3π/2) αA(t) = - 40 ημ(10t + 3π/2)
υmax / υ'max = 0,5 / 4 = 1/8
ΑΣΚΗΣΗ 12
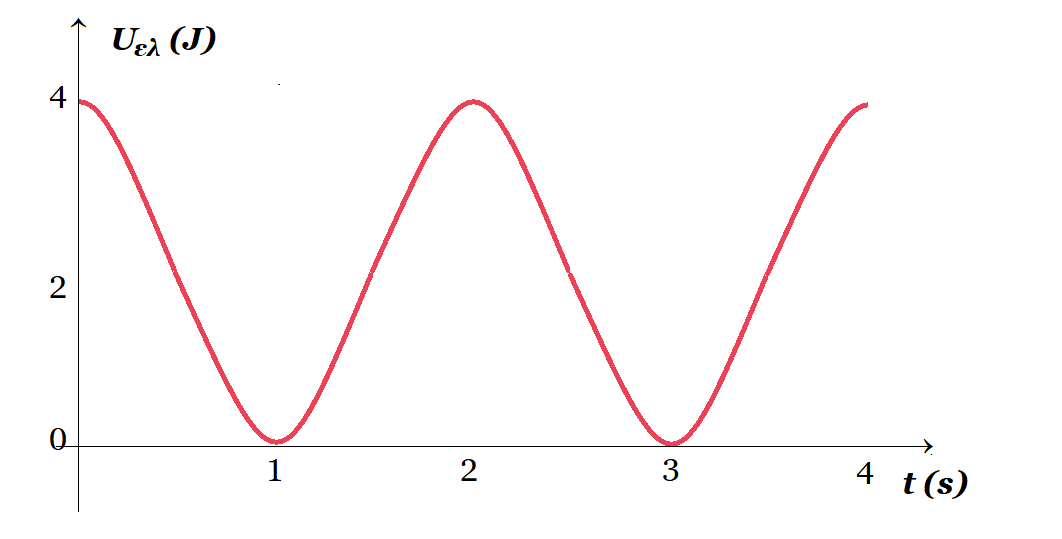
Το γράφημα παριστάνει την δυναμική ενέργεια ενός συστήματος οριζόντιου ελατηρίου και σώματος, μάζας m = 2 kg, που είναι δεμένο στο άκρο του ελατηρίου, σε συνάρτηση με τον χρόνο. Το σύστημα εκτελεί απλή αρμονική ταλάντωση. Χρησιμοποιώντας δεδομένα από τη γραφική παράσταση:
(α) Nα προσδιορίσετε τη μηχανική ενέργεια του συστήματος.
(β) Να προσδιορίσετε την περίοδο της ΑΑΤ του συστήματος.
(γ) Να εξηγήσετε αν οι πληροφορίες που δίνονται επαρκούν για τον προσδιορισμό της αρχικής φάσης της ΑΑΤ που εκτελεί το σύστημα.
(δ) Να υπολογίσετε το πλάτος της ΑΑΤ του συστήματος.
(ε) Να υπολογίσετε τη μεταβολή της κινητικής ενέργειας του συστήματος στο χρονικό διάστημα από 1,5 s μέχρι 2,0 s.
Uελ = ½ k x2 = ½ k Α2 ημ2(ωt + φ) = ½ k Α2 [ 1 - συν2(ωt + φ) ] / 2 =>
=> Uελ (t) = 1/4 k A2[ 1 - συν2(ωt + φ) ]
συν(2ωt) = συν2(ωt) - ημ2(ωt) = 1 - 2ημ2(ωt) => ημ2(ωt) = [ 1 - συν(2ωt) ] / 2
1/4 k Α2 = 2 J Τ = 2 s για την δυναμική ενέργεια Τ = 4 s για την ταλάντωση του σώματος
ω = 2π/Τ = 2π/4 = π/2 rad/s
k = m ω2 => k = 2 (π/2)2 => k = π2/2 N/m
1/4 k Α2 = 2 J => 1/4 π2/2 Α2 = 2 J => A2 = 16 / π2 => A = 4/π m
Uελ (0) = 1/4 k A2[ 1 - συν2φ ] => 4 J = 1/4 π2/2 16 / π2 [ 1 - συν2φ ] =>
=> 4 J = 2 [ 1 - συν2φ ] => 2 = 1 - συν2φ => συν2φ = -1 = συνπ => φ = π/2 rad
τη στιγμή t=0 το σώμα αρχίζει την ταλάντωσή του από ακραία θέση διότι έχει δυναμική ενέργεια 4 J
x(t) = 4/π ημ(π/2 t + π/2) v(t) = 2 συν(π/2 t + π/2) α(t) = - π ημ(π/2 t + π/2)
τη στιγμή t = 1,5 s η δυναμική ενέργεια ταλάντωσης του σώματος είναι 2 J οπότε η κινητική ενέργεια του σώματος θα είναι 4 J - 2 J = 2 J
τη στιγμή t = 2 s η δυναμική ενέργεια ταλάντωσης του σώματος είναι 4 J οπότε η κινητική ενέργεια του σώματος θα είναι 4 J - 4 J = 0 J
συνεπώς η μεταβολή της κινητικής ενέργειας του σώματος από τη στιγμή t = 1,5 s έως τη στιγμή t = 2 s θα είναι ΔΚ = 0 J - 2 J = - 2 J













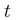 , στο χρονικό διάστημα από
, στο χρονικό διάστημα από