 |<--------------- d -------------->|
|<--------------- d -------------->|
 |<--------------- d -------------->|
|<--------------- d -------------->|
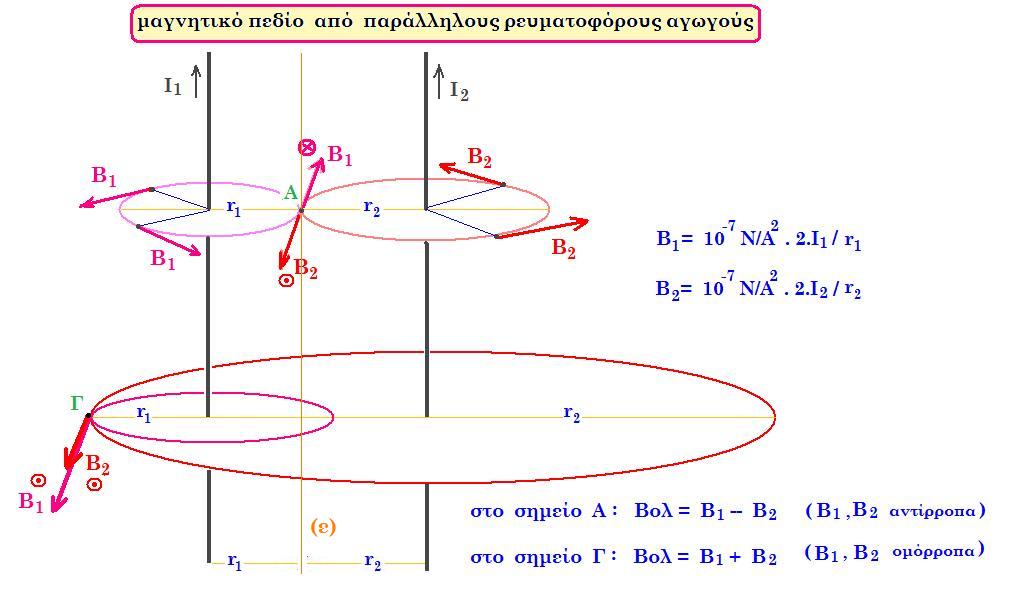
Θεωρούμε πάνω σε λείο οριζόντιο επίπεδο, δύο παράλληλους ευθύγραμμους αγωγούς οι οποίοι διαρρέονται από συνεχή ρεύματα Ι1 και Ι2 Να βρεθούν σημεία του επιπέδου των αγωγών όπου η ένταση του μαγνητικού πεδίου ισούται με μηδέν. Οι αγωγοί απέχουν απόσταση d.
Κάθε αγωγός δημιουργεί γύρω του στον χώρο μαγνητικό πεδίο. Σε σημεία μεταξύ των αγωγών οι εντάσεις Β1 και Β2 των πεδίων είναι αντίρροπες, ενω σε σημεία εκτός των αγωγών είναι ομόρροπες. Έστω σημείο Α μεταξύ των αγωγών που απέχει απόσταση r1 από τον αγωγό που διαρρέεται από το ρεύμα Ι1 και απόσταση r2 από τον αγωγό που διαρρέεται από το ρεύμα Ι2 , έχουμε τη σχέση : Βολ = 0 => Β1 - Β2 = 0 => Β1 = Β2 =>
10-7 Ν/Α2 . 2.Ι1 / r1 = 10-7 Ν/Α2 . 2.Ι2 / r2 =>
Ι1 / r1 = Ι2 / r2 (1) και r1 + r2 = d (2) όλα τα σημεία που ικανοποιούν τις σχέσεις (1) και (2) ανήκουν σε ευθεία (ε) παράλληλη προς τους αγωγούς (βλέπε σχήμα)
Θεωρούμε πάνω σε λείο οριζόντιο επίπεδο, δύο παράλληλους ευθύγραμμους αγωγούς οι οποίοι διαρρέονται από συνεχή ομόρροπα ρεύματα i1 και i2 Μεταξύ των αγωγών θεωρούμε μεταλλική ράβδο μήκους l η οποία είναι παράλληλη στους αγωγούς και διαρρέεται από συνεχές ρεύμα Ι αντίρροπο ως προς τα i1 και i2 Σε ποια απόσταση από τους αγωγούς πρέπει να τοποθετηθεί η ράβδος έτσι ώστε να ισορροπεί; Οι αγωγοί απέχουν απόσταση d.
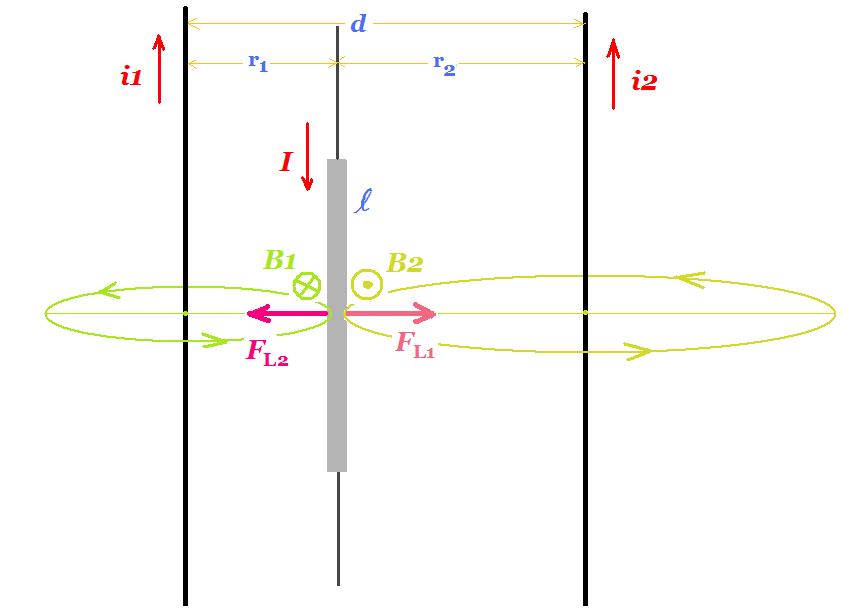
Κάθε αγωγός δημιουργεί γύρω του στον χώρο μαγνητικό πεδίο. Τοποθετούμε την ράβδο όπως στο σχήμα. Η ένταση του μαγνητικού πεδίου από τον αγωγό (1) είναι :
Β1 = 10-7 Ν/Α2.2.i1 / r1 η ράβδος που διαρρέεται από ρεύμα Ι δέχεται δύναμη Laplace : FL1 = B1 . I . l = 10-7 Ν/Α2 . 2.i1 / r1 . I . l = 10-7 Ν/Α2 . 2.I.i1 . l / r1
H ένταση του μαγνητικού πεδίου από τον αγωγό (2) είναι : Β2 = 10-7 Ν/Α2.2.i2 / r2 η ράβδος που διαρρέεται από ρεύμα Ι δέχεται δύναμη Laplace :
FL2 = B2 .I .l = 10-7 Ν/Α2 . 2.i2 / r2 . I . l = 10-7 Ν/Α2 . 2.I.i2 . l / r2
η συνισταμένη δύναμη είναι : ΣF = FL1 - FL2 διότι οι δυνάμεις είναι αντίρροπες.
Για να ισορροπεί η ράβδος πρέπει ΣF = 0 => FL1 = FL2 =>
=> 10-7 Ν/Α2 . 2.I.i1 . l / r1 = 10-7 Ν/Α2 . 2.I.i2 . l / r2 =>
i1 / r1 = i2 / r2 και r1 + r2 = d δηλαδή όπου η ένταση του μαγνητικού πεδίου που δημιουργείται από τους αγωγούς (1) , (2) ισούται με μηδέν
Μετακινούμε την ράβδο παράλληλα κατά x Δείξτε ότι θα κάνει ΑΑΤ με σταθερά επαναφοράς : D = 10-7 Ν/Α2 . 2.I .l .( i2 + i1 )/ r2 .r1

η ράβδος που διαρρέεται από ρεύμα Ι δέχεται δυνάμεις Laplace : F'L1 = 10-7 Ν/Α2 . 2.I .i1.l / (r1 + x) και
F'L2 = 10-7 Ν/Α2 . 2.I .i2 .l / (r2 - x) τότε η συνισταμένη δύναμη :
ΣF = F'L2 - F'L1 =
= 10-7 Ν/Α2 . 2.I .i2 .l / (r2 - x) - 10-7 Ν/Α2 . 2.I .i1 .l / (r1 + x) =
= 10-7 Ν/Α2 . 2.I .l . { i2 / (r2 - x) - i1 / (r1 + x) }
=> ΣF = 10-7 Ν/Α2 . 2.I .l . { (r1 + x). i2 - (r2 - x). i1 } / (r2 - x).(r1 + x) =>
ΣF = 10-7 Ν/Α2 . 2.I .l . { r1 .i2 + x.i2 - i1 .r2 + x. i1 } / (r2 - x).(r1 + x) =>
ΣF = 10-7 Ν/Α2 . 2.I .l .( i2 + i1 ) .x / r2 .r1 διότι x << r1 , x << r2
τελικά ΣF = 10-7 Ν/Α2 . 2.I .l .( i2 + i1 )/ r2 .r1 . x
η ράβδος θα εκτελέση ΑΑΤ με σταθερά :
D = 10-7 Ν/Α2 . 2.I .l .( i2 + i1 )/ r2 .r1