Ορμή - Κρούση ασκήσεις

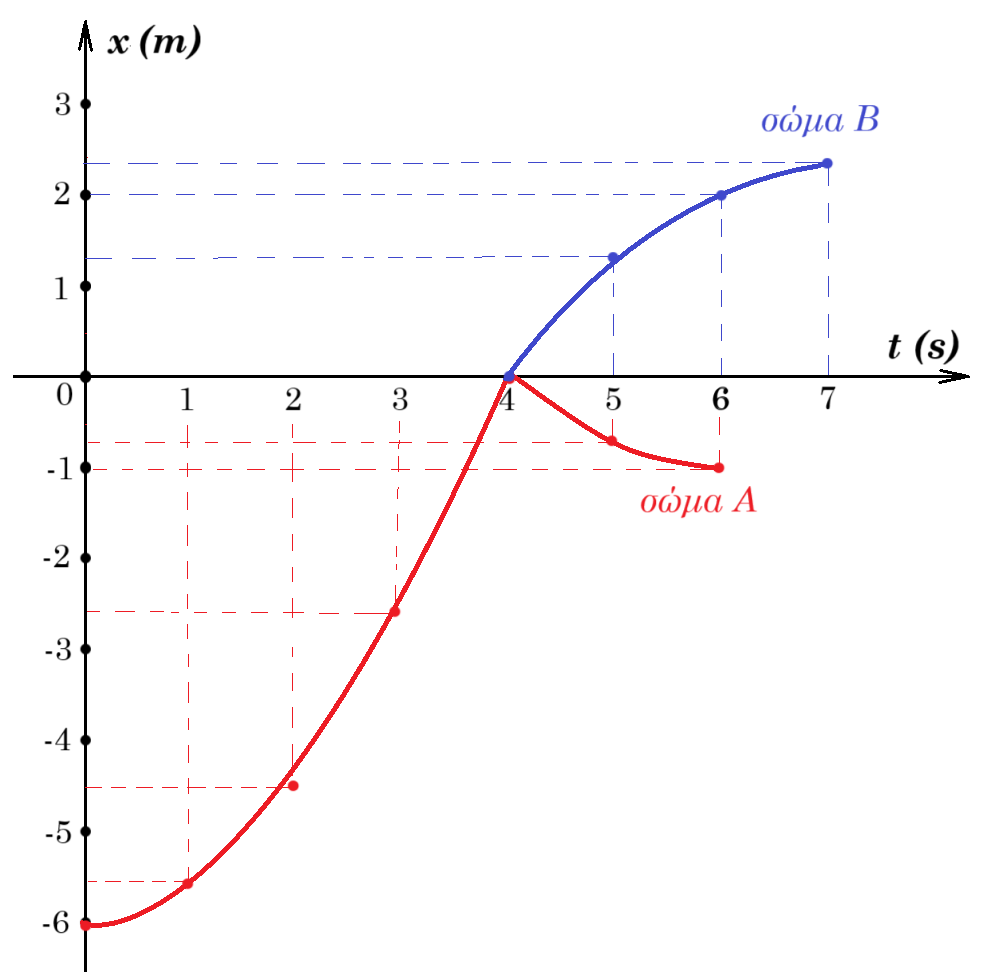
Σώμα Α μάζας m₁=2kg, ηρεμεί σε οριζόντιο επίπεδο. Σε μια στιγμή t₀=0, στο σώμα ασκείται μια σταθερή οριζόντια δύναμη μέτρου F=2,5Ν, μέχρι τη στιγμή t₁, όπου η δύναμη παύει να ασκείται και το σώμα συγκρούεται κεντρικά και ελαστικά με ακίνητο σώμα Β το οποίο βρίσκεται πάνω στον άξονα στη θέση x₀ = 0. Στο σχήμα δίνεται η αλγεβρική τιμή της ταχύτητας του σώματος Α σε συνάρτηση με το χρόνο, όπου η κρούση θεωρείται ακαριαία.

α) Να υπολογισθεί η μεταβολή της ορμής του σώματος Α, στη διάρκεια της κρούσης και η αντίστοιχη μεταβολή της κινητικής του ενέργειας.

β) Αφού εξηγήσετε (χωρίς μαθηματική απόδειξη), γιατί το σώμα Α παρουσιάζει τριβή με το επίπεδο, στη συνέχεια να υπολογίσετε το μέτρο της ασκούμενης τριβής.

γ) Nα βρείτε:

γ₁) Την ενέργεια που μεταφέρεται στο σώμα Α, μέσω του έργου της δύναμης F.

γ₂) Τη χρονική στιγμή t₁ που έγινε η κρούση.

δ) Υπολογίστε την μάζα του σώματος Β. Στη συνέχεια να κάνετε το διάγραμμα της ταχύτητάς του και της θέσης συναρτήσει του χρόνου, με δεδομένο ότι τα δυο σώματα παρουσιάζουν τον ίδιο συντελεστή τριβής με το επίπεδο.

ε) Να κάνετε το διάγραμμα της θέσης του σώματος Α από τη στιγμή t=0 έως τη στιγμή που σταματά να κινείται.

Δp_A = m₁ v₁' - m₁ v₁ = 2 (-1) - 2 3 = - 8 kg^.m/s

ΔΚ = ½ 2 (-1)² - ½ 2 3² = 1 - 9 = - 8 J

επειδή το σώμα Α σταματά να κινείται από τη στιγμή t₁ έως τη στιγμή t₁ + 2s μετά την κρούση χωρίς να δέχεται δύναμη F σημαίνει ότι υπάρχει δύναμη τριβής

σύμφωνα με το διάγραμμα από τη στιγμή t₁ έως τη στιγμή t₁ + 2s το σώμα Α διαανύει διάστημα s₁' = ½ 1m/s 2s => s₁' = 1m

x = 1m = 1m/s 2s - ½ a₁' (2s)² => 1 = 2 - 2 a₁' => a₁' = 0,5 m/s² επιβράδυνση

|Τ₁|= m₁ a₁' = 2 kg 0,5 m/s² => |Τ₁|= 1 N

|Τ₁| = μ m₁ g => 1N = μ 2kg 10m/s² => μ = 1/20 συντελεστής τριβής ολίσθήσεως

πριν την κρούση από τη στιγμή t=0 έως τη στιγμή t₁ ισχύουν :

F - |T₁| = m₁ a₁ => 2,5N - 1N = 2kg a₁ => a₁ = 0,75 m/s²

v₁ = a₁ t₁ => 3 m/s = 0,75 m/s² t₁ => t₁ = 4s x₁ = 0,5 a₁ t₁² = 0,5 0,75 4² => x₁ = 6m

W_F = F s₁' = 2,5N 6m => W_F = 15 J W_T1 = - T₁ s₁' = -1N 6m => W_T1 = -6 J

t = 0s x = - 6 m

t = 1s x = - 6 + 0,5 0,75 1 = - 5,625 m

t = 2s x = - 6 + 0,5 0,75 4 = - 4,5 m

t = 3s x = - 6 + 0,5 0,75 9 = - 2,625 m

t = 4s x = - 6 + 0,5 0,75 16 = 0 m

μετά την κρούση

t = 0s x = 0 m

t = 1s x = - 1 m/s 1 s + 0,5 0,5 1 = - 0,75 m

t = 2s x = - 1 m/s 2 s + 0,5 0,5 4 = - 1 m

ελαστική κρούση

v₁' = v₁ (m₁ - m₂) / (m₁ + m₂) => -1 = 3 (2 - m₂) / (2 + m₂) =>

=> - 2 - m₂ = 6 - 3m₂ => m₂ = 4 kg

v₂' = 2 m₁ v₁ / (m₁ + m₂) = 2 2 3 / (2 + 4) => v₂' = 1,5 m/s προς τα δεξιά

το σώμα Β μετά την κρούση κινείται προς ταα δεξιά επιβραδυνόμενο λόγω τριβών

Τ₂ = μ m₂ g = 1/20 4 10 = 2 N a₂ = μ g = 1/20 10 => a₂ = 0,5 m/s² epibr;adynsh

0 = 1,5 m/s - 0,5 m/s² t₂ => t₂ = 3s

x₂ = 1,5 m/s 3 s - 0,5 0,5 m/s² 9 s² => x₂ = 9/4 m διανύει το Β μέχρι να σταματήσει

t = 0s x = 0

t = 1s x = 1,5 1 - 0,5 0,5 1 = 1,25 m

t = 2s x = 1,5 2 - 0,5 0,5 4 = 2 m

t = 3s x = 1,5 3 - 0,5 0,5 9 = 9/4 m = 2,25 m

Σώμα Α μάζας m₁, ηρεμεί σε λείο οριζόντιο επίπεδο. Σε μια στιγμή t₀=0, στο σώμα ασκείται μια σταθερή οριζόντια δύναμη μέτρου F, με αποτέλεσμα να κινηθεί και μετά από λίγο, τη στιγμή t₁, το σώμα συγκρούεται κεντρικά και ελαστικά με ακίνητο σώμα Β μάζας m₂, ενώ η δύναμη F συνεχίζει να ασκείται στο σώμα Α και μετά την κρούση. Στο σχήμα δίνεται η αλγεβρική τιμή της ταχύτητας του σώματος Α σε συνάρτηση με το χρόνο.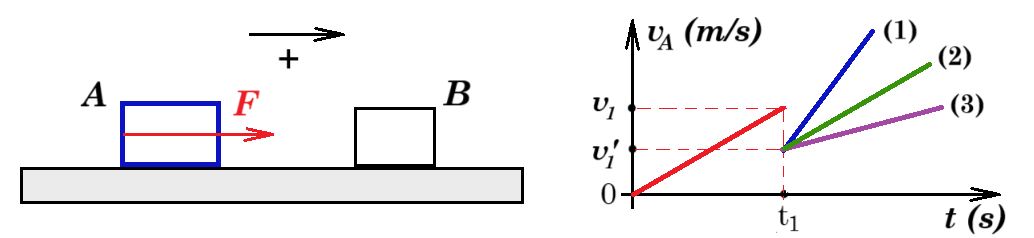

i) Για τις μάζες των δύο σωμάτων ισχύει: α) m₁ < m₂, β) m₁ = m₂, γ) m₁ > m₂.

ii) Η ταχύτητα του Α σώματος μετά την κρούση, ακολουθεί το διάγραμμα (1), (2) ή (3);

iii) Αν η ταχύτητα του σώματος Α αμέσως μετά την κρούση, είναι ίση με το μισό της ταχύτητάς του πριν την κρούση (υ΄₁= ½ υ₁) τότε για την ταχύτητα του σώματος Β μετά την κρούση έχουμε:

α) v₂' = 0,5 v₁ β) v₂' = 1,5 v₁ γ) v₂' = 2,5 v₁ δ) v₂' = 3 v₁

ελαστική κρούση

από το διάγραμμα v(t) έχουμε : v₁' > 0 => v₁' = v₁ (m₁ - m₂) / (m₁ + m₂) > 0 => m₁ > m₂

μετά την κρούση το σώμα Α συνεχίζει να δέχεται την δύναμη F συνεπώς η ειτάχυνση που έχει είναι η ίδια με πριν την κρούση συνεπώς η κλίση της ευθείας ταχύτητα - χρόνος είναι η ίδια με πριν συνεπώς σωστή η (2)

v₁' = v₁ (m₁ - m₂) / (m₁ + m₂) => v₁/2 = v₁ (m₁ - m₂) / (m₁ + m₂) =>

=> m₁ + m₂ = 2 (m₁ - m₂) => m₁ = 3 m₂

v₂' = 2 m₁ v₁ / (m₁ + m₂) = 2 3m₂ v₁ / ( 3m₂ + m₂) = 1,5 v₁

2. Επάνω σε λείο οριζόντιο επίπεδο σφαίρα Σ1 μάζας m₁=m που κινείται με ταχύτητα υ₁, συγκρούεται όχι κεντρικά, με δεύτερη σφαίρα Σ2 μάζας m₂=2m, η οποία είναι αρχικά ακίνητη.
Αμέσως μετά την κρούση, η σφαίρα Σ1 κινείται κάθετα στην αρχική της διεύθυνση με ταχύτητα V₁ και η σφαίρα Σ2 κινείται με ταχύτητα V₂ σε διεύθυνση που σχηματίζει γωνία 30° με την αρχική διεύθυνση κίνησης της σφαίρας Σ1.
I. Το κλάσμα της κινητικής ενέργειας της σφαίρας Σ1 που μεταβιβάστηκε στη Σ2 κατά την κρούση, είναι

(α) 1/2 (β) 2/3 (γ) 1/3
ΙΙ. Το μέτρο μεταβολής της ορμής της σφαίρας Σ1 λόγω κρούση είναι
(α) 2mυ₁ (β) mυ₁√3 (γ) 2mυ₁/√3

m₁ v₁ = m₂ V₂_,x => m v₁ = 2m V₂ συν30° => v₁ = 2 V₂ √3/2 => v₁ = V₂ √3

0 = m₁ V₁ + m₂ V_2,y => m V₁ = - 2m V₂ ημ30° => V₁ = - 2 V₂ ½ => V₁ = - V₂

V₁ = V₂ = v₁ / √3

Κ₁ = ½ m v₁² Κ₁' = ½ m V₁² = ½ m v₁²/3 = K₁ / 3

K₁' / K₁ = 1/3 στη σφαίρα (1) έμεινε το 1/3 της ενέργειάς της

Κ₂' = ½ 2m V₂² = m v₁²/3 = 2/3 K₁ K₂' / K₁ = 2/3 η σφαίρα (2) κέρδισε τα 2/3 της ενέργειας της σφαίρας (1)

Δp₁² = ( m v₁ )² + ( m v₁ / √3 )² = m² v₁² ( 1 + 1/3 ) = 4/3 m² v₁² => Δp₁ = 2mυ₁/√3

εφφ = ( m v₁ / √3 ) / ( m v₁ ) = 1/√3 = √3 / 3 = εφ30°

Δp₂ = p₂' - 0 = p₂' = 2m V₂ = 2m v₁ / √3 |Δp₁| = |Δp₂|

.......................................................................................................................................................

K₁ = p₁² / 2.2m = p₁² / 4m

v₁' = v₁ (2m - m) / (2m + m) = v₁ / 3 p₁' = 2m v₁ / 3 = p₁ / 3 p₁' - p₁ = p₁ /3 - p₁ = - 2p₁ / 3

v₂' = 2 v₁ 2m / (2m + m) = 4v₁ / 3 p₂' = m 4v₁ / 3 = 2p₁ / 3 p₂' - p₂ = 2p₁ / 3 - 0 = 2p₁ / 3

K₂' = (p₂')² / 2m = (2p₁ / 3)² / 2m = 2p₁² / 9m K₂' / K₁ = 8/9

v₁' = v₁ (2m - 3m) / (2m + 3m) = - v₁ / 5 p₁' = 2m (- v₁ / 5) = - p₁ / 5

p₁' - p₁ = - p₁ /5 - p₁ = - 6 p₁ / 5

v₂' = 2 v₁ 2m / (2m + 3m) = 4v₁ / 5 p₂' = 3m 4v₁ / 5 = 6p₁ / 5 = 1,2 p₁

p₂' - p₂ = 6p₁ / 5 - 0 = 6p₁ / 5

K₂' = (p₂')² / 2.3m = (6p₁ / 5)² / 6m = 6p₁² / 25m K₂' / K₁ = 24/25

Δυο μικρές σφαίρες Α και Β, με ίσες ακτίνες και με μάζες m₁=3m και m₂=m κινούνται στην ίδια ευθεία σε λείο οριζόντιο επίπεδο. Η σφαίρα Α κινείται προς τα δεξιά (όπου ορίζουμε την θετική κατεύθυνση) με σταθερή ταχύτητα υ₁=4m/s και κάποια στιγμή συγκρούεται κεντρικά και ελαστικά με την σφαίρα Β.

Ποιες οι δυνατές τιμές ταχύτητας της σφαίρας Β, ώστε να έχουμε κρούση μεταξύ των δύο σφαιρών;
Να βρείτε μια σχέση που να δίνει την ταχύτητα της σφαίρας Α μετά την κρούση, σε συνάρτηση με την ταχύτητα της σφαίρας Β, πριν την κρούση, κάνοντας και την γραφική της παράσταση. (υ₁΄=f(υ₂)). Στο διάγραμμα να σημειωθούν χαρακτηριστικές τιμές για τις ταχύτητες των δύο σφαιρών.
Να υπολογιστεί η ταχύτητα της σφαίρας Β υ₂ πριν την κρούση, αν η σφαίρα Α χάνει το 75% της κινητικής της ενέργειας κατά την κρούση.
Να βρεθεί η κινητική ενέργεια της Β σφαίρας μετά την κρούση, αν κατά την κρούση η σφαίρα Α χάσει το 100% της κινητικής της ενέργειας, ενώ m=1kg.

για να έχουμε κρούση πρέπει v₁ > v₂ => v₂ < 4 m/s

v₁' = v₁ (m₁ - m₂) / (m₁ + m₂) + 2 m₂ v₂ / (m₁ + m₂) = 4 (3m - m) / (3m + m) + 2 m v₂ / (3m + m) = 2 + v₂ / 2 => v₁' = 2 + 0,5 v₂ v₁' < 2 + 0,5 4 m/s = 4 m/s

v₂' = v₂ (m₂ - m₁) / (m₁ + m₂) + 2 m₁ v₁ / (m₁ + m₂) = v₂ (m - 3m) / (3m + m) + 2 3m 4 / (3m + m) = - v₂ / 2 + 6 => v₂' = 6 - 0,5 v₂

v₂ < 4 m/s => - 0,5 v₂ > - 0,5 4 m/s => v₂' > 6 - 2 = 4 m/s

K₁ = 0,5 m₁ v₁² = 0,5 3m 4²

K₁' = 0,25 K₁ => (v₁')² = 0,25 v₁² => v₁' = 0,5 v₁ => 2 + 0,5 v₂ = 0,5 4 => v₂ = 0

ή v₁' = - 0,5 v₁ => 2 + 0,5 v₂ = - 0,5 4 => v₂ = - 8 m/s

K₁' = 0 => v₁' = 0 => 2 + 0,5 v₂ = 0 => v₂ = - 4 m/s v₂' = 6 - 0,5 v₂ = 6 - 0,5 (- 4) = 8 m/s

K₂' = 0,5 m₂ (v₂')² = 0,5 1 8² = 32 J

Μια ελαστική αλλά όχι λεία σφαίρα ακτίνας 0,1 m πέφτει σε ελαστικό αλλά όχι λείο τοίχο.

Η ταχύτητα της σφαίρας είναι 10√2 m/s και η γωνία πρόσπτωσης 45^ο.

Εκτελεί αρχικά μεταφορική κίνηση.

Μετά την κρούση ανακλάται με γωνία φ τέτοια ώστε εφφ = 4/5.

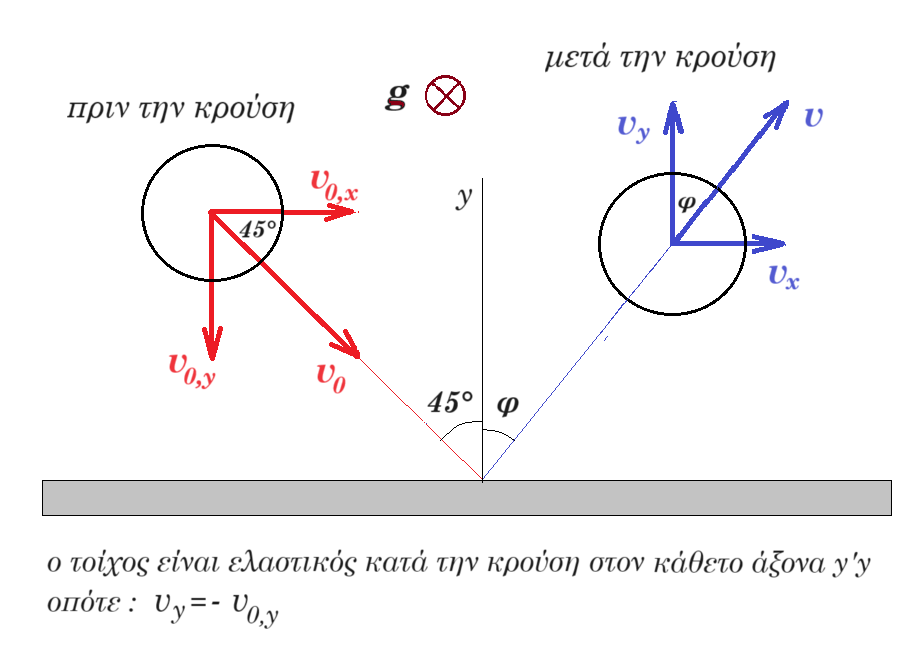
Να βρείτε την ταχύτητα και την γωνιακή ταχύτητα της σφαίρας μετά την ανάκλαση.
Να βρείτε τον συντελεστή τριβής μεταξύ σφαίρας και τοίχου.

άξονας x'x : v₀ √2/2 = v_x => v_x = 10√2 √2/2 = 10 m/s

επειδή v_y / v_x = εφφ = 4/5 => v_y / v_x = εφφ = 4/5 => v_y = v_x 4/5 => v_y = 10 4/5 = 8 m/s

άξονας y'y : v₀ √2/2 = v ημφ

Στ = Ι α_γων => T r = 2/5 m r² α_γων => T = 2/5 m r α_γων =>

Δύο όμοιες λείες και ελαστικές σφαίρες κινούνται σε οριζόντιο λείο δάπεδο.

Μετά την κρούση η σφαίρα (2) κινείται με ταχύτητα ίδιας διεύθυνσης αλλά αντίθετης φοράς από την αρχική της.

Να βρεθούν οι ταχύτητες μετά την κρούση.

Δίδεται ότι υ₁ = 5 m/s , υ₂ = 3 m/s , ημφ = 3/5 , συνφ = 4/5.

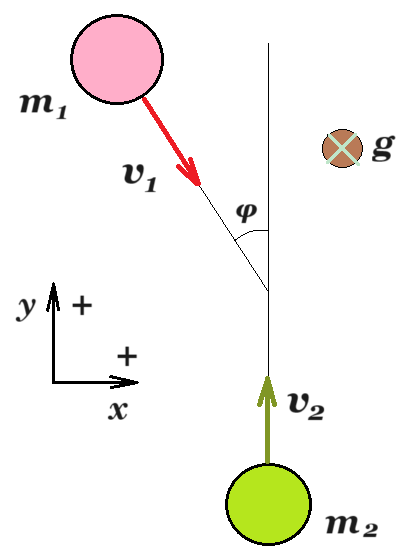άξονας x : m v₁ ημφ = m v₁' => v₁ ημφ = v_1,x' => v_1,x' = 5 3/5 = 3 m/s

άξονας y : - m v₁ συνφ + m v₂ = m v_1,y' - m v₂' => - 5 4/5 + 3 = v_1,y' - v₂' => v_1,y' = v₂' - 1m/s

½ m v₁² + ½ m v₂² = ½ m (v₁')² + ½ m (v₂')²

v₁² + v₂² = (v_1,x')² + (v_1,y')² + (v₂')²

5² + 3² = 3² + (v₂' - 1)² + (v₂')²

25 = (v₂' - 1)² + (v₂')²

25 = (v₂')² + 1² - 2 v₂' + (v₂')²

2 (v₂')² - 2 v₂' - 24 = 0

(v₂')² - v₂' - 12 = 0 => (v₂' - 4) (v₂' + 3) = 0 =>

v₂' = 4 m/s v_1,y' = v₂' - 1m/s = 4 m/s - 1 m/s = 3 m/s

v₂' = - 3 m/s δεκτή v_1,y' = v₂' - 1m/s = - 3 m/s - 1 m/s = - 4 m/s

(v₁')² = (v_1,x')² + (v_1,y')² = 3² + 3² => v₁' = 3√2 m/s

(1) Σώμα μάζας m που κινείται με ταχύτητα υ συγκρούεται κεντρικά και πλαστικά με αρχικά ακίνητο σώμα μάζας 3m.
Το ποσοστό απώλειας ενέργειας του συστήματος κατά την πλαστική κρούση ισούται με:
i. 50%. ii. 25%. iii. 75%

(2) Σφαίρα μάζας m₁κινείται με ορμή μέτρου p₁και συγκρούεται, κεντρικά και ελαστικά, με ακίνητη σφαίρα μάζας m₂. Μετά την κρούση η σφαίρα μάζας m₁ έχει ορμή p₁' = p₁/ 5.
Το ποσοστό της κινητικής ενέργειας που μεταβιβάστηκε από τη σφαίρα μάζας m₁στη σφαίρα μάζας m₂κατά την κρούση είναι ίσο με:
i. 64%. ii. 80%. iii. 96%.

(3) Μικρό σώμα Σ1 μάζας m που κινείται με ταχύτητα υ συγκρούεται κεντρικά με αρχικά ακίνητο μικρό σώμα Σ2 μάζας 2m.
Μετά την κρούση το σώμα Σ1 παραμένει ακίνητο. Μετά την κρούση η κινητική ενέργεια του συστήματος των δύο σωμάτων
α. αυξήθηκε. β. παρέμεινε η ίδια. γ. ελαττώθηκε.

(4) Σώμα, Α, μάζας m συγκρούεται με έκκεντρα με σώμα Β, μάζας 2m που αρχικά είναι ακίνητο. Μετά την κρούση το σώμα Α φεύγει με ταχύτητα που σχηματίζει γωνία θ=30° με τον φορέα της ταχύτητας που είχε πριν την κρούση. Το σώμα Β μετά την κρούση έχει ταχύτητα που σχηματίζει γωνία φ=45° με τον με τον φορέα της ταχύτητας που είχε το Α πριν την κρούση.
I. Ο λόγος V_A/V_B των ταχυτήτων των δύο σωμάτων μετά την κρούση είναι:
α. v_A/v_B = √2/2 β. v_A/v_B=2√2 γ. v_A/v_B=√2
II. H κρούση είναι:
α. Ελαστική β. Ανελαστική

(5) Σε λείο οριζόντιο επίπεδο μια σφαίρα Σ₁μάζας m μικρών διαστάσεων συγκρούεται ελαστικά, αλλά όχι κεντρικά, με δεύτερη όμοια σφαίρα Σ₂ίσης μάζας m, η οποία είναι αρχικά ακίνητη.
Μετά την κρούση οι σφαίρες Σ₁και Σ₂κινούνται με ταχύτητες υ₁ και υ₂ αντίστοιχα. Η γωνία που σχηματίζει το διάνυσμα της ταχύτητας υ₁ με το διάνυσμα της ταχύτητας υ₂ είναι:
i. 60° ii. 90° iii. 120°

(6) Δύο σφαίρες, ίσων μαζών, συγκρούονται ελαστικά. Αν υ₁, υ₂ και υ₁' και υ₂' είναι τα μέτρα των ταχυτήτων πριν και μετά την κρούση, αντίστοιχα, και φ η γωνία που σχημάτιζαν οι διευθύνσεις των ταχυτήτων πριν την κρούση, να βρείτε τη γωνία θ που σχηματίζουν οι διευθύνσεις των ταχυτήτων μετά την κρούση. φ = 30^ο, υ₁ = 20 m/s, υ₂ = 10 m/s, υ₁' = 10√3 m/s.

(7) Δύο σώματα με μάζες m₁=2kg και m₂=3kg κινούνται χωρίς τριβές στο ίδιο οριζόντιο επίπεδο και σε κάθετες διευθύνσεις με ταχύτητες υ₁= 4m/s και υ₂= 2m/s και συγκρούονται πλαστικά. Η κινητική ενέργεια του συσσωματώματος είναι :

α) 5 J β) 10 J γ) 20 J

(8) Δύο σώματα Α και Β με μάζες m και 4m αντίστοιχα, κινούνται πάνω στην ίδια ευθεία με αντίθετη φορά. Τα δύο σώματα έχουν ίσες κινητικές ενέργειες και συγκρούονται μετωπικά και πλαστικά. Αν υ₁είναι το μέτρο της ταχύτητας του σώματος Α και V το μέτρο της ταχύτητας του συσσωματώματος που δημιουργείται μετά την κρούση, τότε:

α) V = υ₁ / 5 β) V = 2υ₁ / 5 γ) V = 3υ₁ / 5

(9) Ένα σώμα Σ₁με μάζα m₁= 1kg κινείται με ταχύτητα υ₁= 10m/s σε λείο οριζόντιο επίπεδο και κατά μήκος του άξονα x΄x. Το σώμα Σ₁συγκρούεται κεντρικά και ελαστικά με ακίνητο σώμα Σ₂μάζας m₂= 3kg που βρίσκεται στο ίδιο οριζόντιο επίπεδο με το Σ₁. Η διάρκεια της κρούσης θεωρείται αμελητέα και η φορά της ταχύτητας υ₁θετική. Να υπολογίσετε:
α. την ταχύτητα του Σ₁μετά την κρούση
β. την ταχύτητα του Σ₂μετά την κρούση
γ. την κινητική ενέργεια του συστήματος των δύο σωμάτων μετά την κρούση τους
δ. την μεταβολή της ορμής των σωμάτων λόγω της κρούσης.

(10) Σε λείο οριζόντιο επίπεδο σφαίρα Σ₁μάζας m₁= m που κινείται με ταχύτητα υ₁, συγκρούεται ελαστικά, αλλά όχι κεντρικά, με δεύτερη σφαίρα Σ₂μάζας m₂= 2m, η οποία είναι αρχικά ακίνητη. Αμέσως μετά την κρούση, η σφαίρα Σ₁κινείται κάθετα στην αρχική της διεύθυνση με ταχύτητα υ₁' και η σφαίρα Σ₂κινείται με ταχύτητα υ₂' σε διεύθυνση που σχηματίζει γωνία 30° με την αρχική διεύθυνση κίνησης της σφαίρας Σ₁. Στη συνέχεια, η σφαίρα Σ₁συγκρούεται κεντρικά και πλαστικά με ακίνητη σφαίρα Σ₃μάζας m₃= m που βρίσκεται ακίνητη στο ίδιο λείο οριζόντιο επίπεδο. Ο λόγος της τελικής κινητικής ενέργειας του συσσωματώματος των σφαιρών Σ₁και Σ₃προς την αρχική κινητική ενέργεια της σφαίρας Σ₁, πριν την κρούση της με τη σφαίρα Σ₂, είναι ίσος με:

α) 1/2 β) 1/3 γ) 1/6

(1) διατήρηση ορμής : m v = (m + 3m) V => V = v / 4

(K_τελ - Κ_αρχ) / Κ_αρχ = ( ½ 4m V² - ½ m v² ) / ½ m v² = 4 (V/v)² - 1 = 4 ( 1/4 )² - 1 = 1/4 - 1 = - 3/4 -75%

(2) p₁' = p₁ / 5 ( K₁' - K₁ ) / K₁ = ( p₁' / p₁ )² - 1 = 0,2² - 1 = - 0,96 - 96%

(3) διατήρηση ορμής : m v₁ = 2m v₂' => v₁ = 2 v₂'

Κ_αρχ - Κ_τελ = ½ m v₁² - ½ 2m (v₂')² = ½ m 4 (v₂')² - ½ 2m (v₂')² > 0 απώλεια ενέργειας

(4) άξονας y : 0 = m v_A ημ30° - 2m v_Β ημ45° => m v_A 1/2 = 2m v_Β √2/2 => v_A/ v_Β = 2√2

άξονας x : m v₀ = m v_A συν30° + 2m v_Β συν45° => v₀ = v_A _√3/2 + 2 v_Β √2/2 =>

=> v₀ = v_Β 2√2 √3/2 + v_Β √2 => v₀ = v_Β √2 √3 + v_Β√2 => v₀ = v_Β √2 (√3 + 1)

Κ_αρχ = ½ m v₀² = ½ m 2 v_Β² (4 + 2√3) = (8 + 4√3) ½ m v_Β²

Κ_τελ = ½ m v_Α² + ½ 2m v_Β² = ½ m 8v_Β² + ½ 2m v_Β² = 10 ½ m v_Β²

(8 + 4√3) > 10 => Κ_αρχ > Κ_τελ ανελαστική κρούση απώλεια ενέργειας

(5) διανυσματικά έχουμε : p₁² = (p₁')² + (p₂')² + 2 (p₁') (p₂') συνθ (1)

διατήρηση ενέργειας : Κ₁ = Κ₁' + Κ₂' => p₁²/ 2m = (p₁')²/ 2m + (p₂')²/ 2m => p₁² = (p₁')² + (p₂')² (2)

(1) , (2) => συνθ = 0 => θ = 90°

(6) διατήρηση ορμής : p₁² + p₂² + 2 p₁ p₂ συνφ = (p₁')² + (p₂')² + 2 p₁' p₂' συνθ

επειδή οι μάζες είναι ίσες v₁² + v₂² + 2 v₁ v₂ συνφ = (v₁')² + (v₂')² + 2 v₁' v₂' συνθ (1)

διατήρηση ενέργειας : ½ m v₁² + ½ m v₂² = ½ m (v₁')² + ½ m (v₂')² => v₁² + v₂² = (v₁')² + (v₂')² (2)

(1) , (2) => 2 v₁ v₂ συνφ = 2 v₁' v₂' συνθ => v₁ v₂ συνφ = v₁' v₂' συνθ (3)

εφαρμογή :

η (2) => v₁² + v₂² = (v₁')² + (v₂')² => 20² + 10² = (10√3)² + (v₂')² =>

=> 400 + 100 = 300 + (v₂')² => (v₂')² = 200 => v₂' = 10√2 m/s

(3) => v₁ v₂ συνφ = v₁' v₂' συνθ => 20 10 συν30° = 10√3 10√2 συνθ =>

=> 20 10 √3/2 = 10√3 10√2 συνθ => συνθ = 1/√2 = √2/2 = συν45°

(7) διατήρηση ορμής : p₁² + p₂² + 2 p₁ p₂ συν90° = (p')² => 8² + 6² = (p')² = 100

K = (p')² / 2(m₁ + m₂) = 100 / 2.(2 + 3) = 10 J

(8) K₁ = K₂ => ½ m v₁² = ½ 4m v₂² => v₁² = 4 v₂² => |v₁| = 2 |v₂|

διατήρηση ορμής : m v₁ - 4m v₂ = (m + 4m) V => v₁ - 4 v₂ = 5 V =>

=> v₁ - 4 v₁/2 = 5 V => v₁ - 2 v₁ = 5 V => V = - v₁ / 5

(9) v₁' = v₁ (m₁ - m₂) / (m₁ + m₂) + 2 v₂ m₂ / (m₁ + m₂) => v₁' = 10 (1 - 3) / (1 + 3) = - 5 m/s

v₂' = v₂ (m₂ - m₁) / (m₁ + m₂) + 2 v₁ m₁ / (m₁ + m₂) => v₂' = 2 10 1 / (1 + 3) = + 5 m/s

K₁ + K₂ = ½ m₁ (v₁')² + ½ m₂ (v₂')² = ½ 1 (- 5)² + ½ 3 (+ 5)² = 50 J

Δp₁ = m₁ v₁' - m₁ v₁ = 1 (- 5) - 1 10 = - 15 kg m/s

Δp₂ = m₂ v₂' - m₂ v₂ = 3 (+ 5) = + 15 kg m/s

(10) άξονας y : 0 = m v₁' - 2m v₂' ημ30° => v₁' = 2 v₂' ½ => v₁' = v₂' οι ταχύτητες των σωμάτων μετά την κρούση έχουν ίσα μέτρα

άξονας x : m v₁ = 2m v₂' συν30° => v₁ = 2 v₂' _√3/2 => v₁ = v₂' _√3

m v₁' = 2m V => V = v₁'/ 2

K_1,3 = 0,5 2m V² = m (v₁')² / 4 = m ( v₁²/3 ) / 4 = ½ m v₁²/ 6 = Κ₁ / 6

Λεία σφαίρα Σ1 μάζας m₁ = m, κινείται κατά τη θετική φορά ενός άξονα Χ΄Χ με ταχύτητα μέτρου υ₁= √2m/s. Δεύτερη επίσης λεία σφαίρα Σ2, μάζας m₂ = m/3, που κινείται κατά την αρνητική φορά του άξονα Χ΄Χ, με ταχύτητα μέτρου υ₂, συγκρούεται με την Σ1. Μετά την κρούση, η σφαίρα Σ1 κινείται με ταχύτητα μέτρου υ₁΄= υ₁/2 κατά την αρνητική φορά του άξονα Ψ΄Ψ ενώ η Σ2 κινείται με ταχύτητα μέτρου υ₂΄, υπό γωνία φ = 45⁰, ως προς τον θετικό ημιάξονα x'x.

α) Υπολογίστε τις ταχύτητες υ₂ και υ₂΄ και της σφαίρας Σ2.

β) Η κρούση είναι ελαστική; Δικαιολογήστε την απάντησή σας.

γ) Αν m = 3kg, ποια είναι η μεταβολή της ορμής κάθε σφαίρας;

~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~

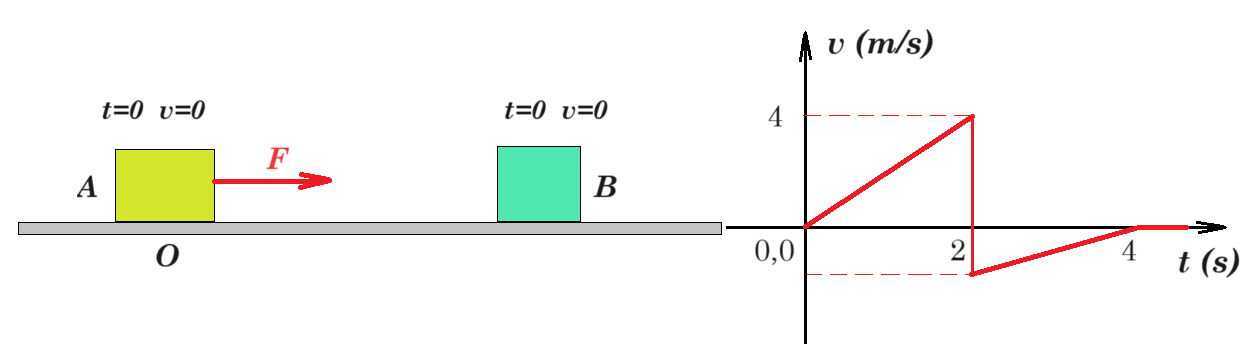Σε οριζόντιο επίπεδο ηρεμούν δύο σώματα Α και Β τα οποία εμφανίζουν με το επίπεδο, τον ίδιο συντελεστή τριβής ολίσθησης. Σε μια στιγμή t=0, ασκείται στο σώμα Α μια οριζόντια δύναμη μέτρου F=1,2Ν, με κατεύθυνση προς το σώμα Β, με το οποίο συγκρούεται κεντρικά και ελαστικά, ενώ ταυτόχρονα παύει να ασκείται πάνω του η δύναμη F. Το σώμα Α σταματά τελικά σε απόσταση d₁=2m, από την αρχική του θέση Ο, ενώ στο διάγραμμα δίνεται η ταχύτητά του, σε συνάρτηση με το χρόνο.

Να υπολογιστεί η μάζα m₁ του σώματος Α.
Ποια η ταχύτητα του Α σώματος, αμέσως μετά την κρούση;
Να βρεθεί η μάζα του Β σώματος.
Ποια η τελική απόσταση μεταξύ των δύο σωμάτων, όταν ακινητοποιηθούν ξανά;

διατήρηση ορμής στον άξονα y'y :

0 = m/3 v₂' √2/2 - m √2/2 => 1/3 v₂' √2/2 = √2/2 => v₂' = 3 m/s

διατήρηση ορμής στον άξονα x'x :

m √2 - m/3 v₂ = m/3 v₂' √2/2 => 3√2 - v₂ = v₂' √2/2 => 3√2 - v₂ = 3 √2/2 => v₂ = 3√2/2 m/s

κινητική ενέργεια πριν την κρούση :

K = ½ m (√2)² + ½ m/3 (3√2/2)² = ½ m 2 + ½ m/3 9/2 = m + 3m/4 = 7m/4

κινητική ενέργεια μετά την κρούση :

K' = ½ m (√2/2)² + ½ m/3 3² = ½ m 1/2 + ½ m/3 9 = m/4 + 3m/2 = 7m/4

ελαστική κρούση έχουμε διατήρηση ενέργειας

Δp_1,x = 0 - m √2 = - 3√2 kg m/s Δp_1,y = - m √2/2 - 0 = - 3√2/2 kg m/s

Δp₁² = (- 3√2)² + (- 3√2/2)² = 18 + 9/2 = 45/2 => Δp₁ = 3√5/2 kg m/s

υπό γωνία θ : εφθ = (- 3√2/2) / (- 3√2) = 1/2

Δp_2,x = m/3 3 συν45° - (- m/3 3√2/2 ) = 3/3 3 √2/2 + 3/3 3√2/2 = 3√2 kg m/s

Δp_2,y = m/3 3 ημ45° - 0 = 3/3 3 √2/2 = 3√2/2 kg m/s

Δp₂² = (3√2)² + (3√2/2)² = 18 + 9/2 = 45/2 => Δp₂ = 3√5/2 kg m/s

υπό γωνία θ : εφθ = (+3√2/2) / (+3√2) = 1/2

~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~

a₁ = v₁ / t₁ = 4 m/s / 2 s = 2 m/s² (1) a₁' = v₁' / t₁' = v₁' / 2 s (2)

F - T = m₁ a₁ => F - μ m₁ g = m₁ a₁ => 1,2 N - μ m₁ 10 m/s² = m₁ 2 m/s² (3)

το σώμα Α μετατοπίζεται προς τα αριστερά η δύναμη τριβής είναι αντίρροπη της ταχύτητας (προς τα δεξιά)

T = m₁ a₁' => μ m₁ g = m₁ a₁' => a₁' = μ g = μ 10 m/s² (4)

v₁' = - μ g 2 s = - μ 10 m/s² 2 s = - μ 20 m/s (5)

d₁ = 0,5 a₁ t₁² + v₁' t₁' + 0,5 a₁' (t₁')² =>

=> 2 m = 0,5 2 m/s² 4 s² - μ 20 m/s 2 s + 0,5 μ 10 m/s² 4 s² =>

=> 2 m = 4 m - μ 40 m/s + μ 20 m/s => μ = 0,1 (6)

(4) => a₁' = μ 10 m/s² = 0,1 10 m/s² => a₁' = 1 m/s²

(5) => v₁' = - μ 20 m/s = - 0,1 20 m/s => v₁' = - 2 m/s

(3) => 1,2 N - μ m₁ 10 m/s² = m₁ 2 m/s² => 1,2 N - 0,1 m₁ 10 m/s² = m₁ 2 m/s² =>

=> 1,2 N = m₁ 3 m/s² => m₁ = 0,4 kg

v₁' = v₁ (m₁ - m₂) / (m₁ + m₂) => - 2 = 4 (0,4 - m₂) / (0,4 + m₂) =>

=> - 2 (0,4 + m₂) = 4 (0,4 - m₂) => - (0,4 + m₂) = 2 (0,4 - m₂) =>

=> - 0,4 - m₂ = 0,8 - 2m₂ => m₂ = 1,2 kg

v₂' = 2 v₁ m₁ / (m₁ + m₂) = 2 4 0,4 / (0,4 + 1,2) => v₂' = + 2 m/s

- T = m₂ a₂ => - μ m₂ g = m₂ a₂ => a₂ = - μ g = - 0,1 10 = - 1 m/s² επιβράδυνση

0 = v₂' + a₂ t₂ => 0 = 2 m/s + (- 1 m/s² ) t₂ => t₂ = 2 s

x₂ = v₂' t₂ + 0,5 a₂ (t₂)² = 2 m/s 2 s + 0,5 (- 1 m/s²) 4 s² = 4 m - 2 m = 2 m

το σώμα Α διανύει 4 m μέχρι να συγκρουσθεί με το σώμα Β, μετά διανύει 2 m προς τα αριστερά και απέχει 2 m από την αφετηρία Ο

το σώμα Β απέχει αρχικά 4 m από την αφετηρία Ο και μετά την κρούση διανύει 2 m μέχρι να σταματήσει

τελικά τα σώματα απέχουν 4 m

Σφαίρα μάζας m₁πέφτει με ταχύτητα υ₁σε ακίνητη σφαίρα μάζας m₂και συγκρούεται ελαστικά και κεντρικά με αυτή. Ποια πρέπει να είναι η σχέση μεταξύ των m₁και m₂ώστε μετά την κρούση η σφαίρα m₂να έχει μέγιστη κινητική ενέργεια;

m₁ v₁ = m₁ v₁' + m₂ v₂'

v₁' = v₁ (m₁ - m₂) / (m₁ + m₂) + 2 v₂ m₂ / (m₁ + m₂)

v₂' = v₂ (m₂ - m₁) / (m₁ + m₂) + 2 v₁ m₁ / (m₁ + m₂)

για να έχει το σώμα (2) μέγιστη κινητική ενέργεια πρέπει το σώμα (1) να έχει ελάχιστη κινητική ενέργεια άρα ελάχιστη ταχύτητα αυτό συμβαίνει όταν m₁ = m₂ οπότε v₁' = 0

v₁' = v₁ (m₁ - m₂) / (m₁ + m₂) + 2 v₂ m₂ / (m₁ + m₂)

v₁' = 4 (2 - 4) / 6 + 2 (-5) 4 / 6 = - 8/6 - 40/6 = - 48/6 = - 8 m/s

v₂' = v₂ (m₂ - m₁) / (m₁ + m₂) + 2 v₁ m₁ / (m₁ + m₂)

v₂' = - 5 (4 - 2) / 6 + 2 4 2 / 6 = - 10/6 + 16/6 = + 1 m/s

v₁' = v₁ (m₁ - m₂) / (m₁ + m₂) + 2 v₂ m₂ / (m₁ + m₂)

v₁' = v₁ (1 - m₂) / (1 + m₂) = v₁/3 => (1 - m₂) / (1 + m₂) = 1/3 => 3(1 - m₂) = (1 + m₂) => 3 - 3m₂ = 1 + m₂ => 2 = 4m₂ => m₂ = 0,5 kg

v₂' = 2 v₁ m₁ / (m₁ + m₂) = 2 v₁ 1 / (1 + 0,5) = 4/3 v₁

v₁' = v₁ (1 - m₂) / (1 + m₂) = - v₁/3 => (1 - m₂) / (1 + m₂) = - 1/3 => -3(1 - m₂) = (1 + m₂) => - 3 + 3m₂ = 1 + m₂ => 4 = 2m₂ => m₂ = 2 kg

v₂' = 2 v₁ m₁ / (m₁ + m₂) = 2 v₁ 1 / (1 + 2) = 2/3 v₁

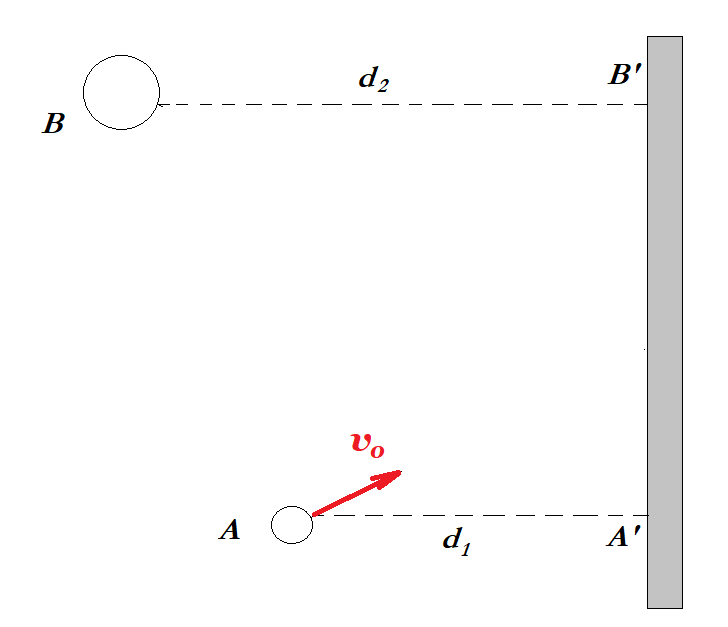Σε λείο οριζόντιο επίπεδο ηρεμούν δυο μικρές σφαίρες με μάζες m₁ = 0,2 kg και m₂ = 0,8 kg αντίστοιχα στα σημεία Α και Β. Οι σφαίρες απέχουν από κατακόρυφο τοίχο αποστάσεις d₁ = (ΑΑ') = 1,2 m και d₂= (ΒΒ΄) = 2 m, ενώ (Α΄Β΄) = D = 2,4 m. Τη στιγμή t = 0, η πρώτη σφαίρα δέχεται κατάλληλο κτύπημα αποκτώντας ταχύτητα υ₀, με αποτέλεσμα, μετά την ελαστική κρούση της με τον τοίχο, να συγκρουσθεί τη στιγμή t₁ = 2 s με τη δεύτερη σφαίρα κεντρικά και ελαστικά.
i) Σε ποιο σημείο του τοίχου έγινε η ανάκλαση της σφαίρας και ποιο το μέτρο της αρχικής ταχύτητας υ₀;
ii) Να υπολογισθεί η μεταβολή της ορμής της σφαίρας κατά την κρούση της με τον τοίχο.
iii) Θα επιστρέψει ξανά η πρώτη σφαίρα στην αρχική της θέση Α και αν ναι, ποια χρονική στιγμή θα συμβεί αυτό;
Ο τοίχος είναι λείος και η διάρκεια των κρούσεων αμελητέα.

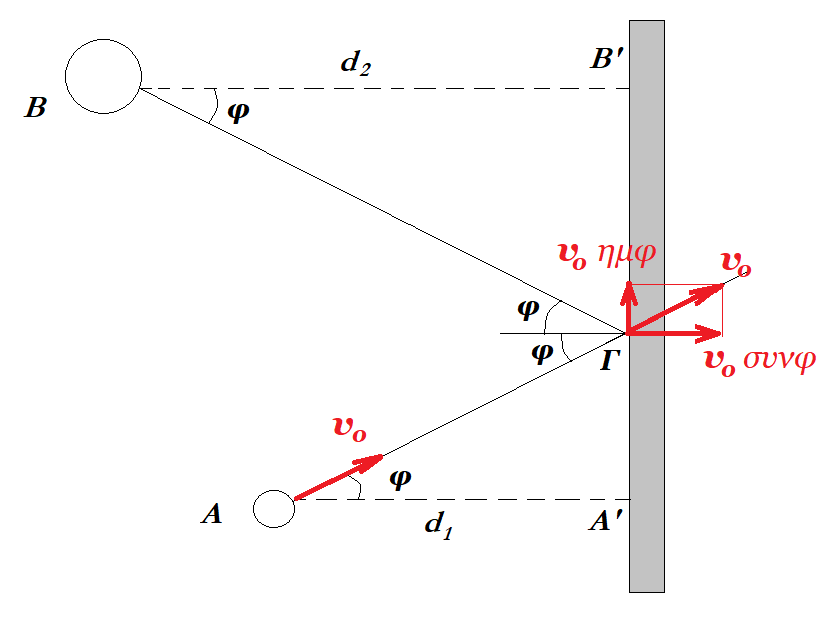
τα ορθογώνια τρίγωνα ΒΒ'Γ και ΑΑ'Γ είναι όμοια : (Α'Γ) / (ΑΑ') = (Β'Γ) / (ΒΒ') =>

=> (Α'Γ) / 1,2 = ( 2,4 - (Α'Γ) ) / 2 => ... => (Α'Γ) = 0,9 m (Β'Γ) = 2,4 - 0,9 = 1,5 m

(AΓ)² = (ΑΑ')² + (Α'Γ)² = 1,2² + 0,9² = 1,5² => (ΑΓ) = 1,5 m

(BΓ)² = (BB')² + (B'Γ)² = 2² + 1,5² = 2,5² => (BΓ) = 2,5 m συνφ = (ΑΑ') / (ΑΓ) = 1,2 / 1,5 = 3/4

(ΑΓ) + (BΓ) = v₀ t => 1,5 + 2,5 = v₀ 2 => v₀ = 2 m/s

Δp₁ = - m₁ v₀ συνφ - m₁ v₀ συνφ = - 2 m₁ v₀ συνφ = - 2 0,2 2 3/4 = - 0,6 kg m/s

ελαστική κρούση : v_A = v₀ (m₁ - m₂) / (m₁ + m₂) = 2 ( 0,2 - 0,8 ) / ( 0,2 + 0,8 ) = - 1,2 m/s

v_B = 2 v₀ m₁ / (m₁ + m₂) = 2 2 0,2 / ( 0,2 + 0,8 ) = 0,8 m/s

(ΑΓ) + (BΓ) = v_A t' => 1,5 + 2,5 = 1,2 t' => t' = 10/3 s

μαθηματική ανάλυση :

(ΑΓ) + (BΓ) = v₀ t => √( x² + 1,2² ) + √( 2² + (2,4 - x)² ) = v₀ t (1)

(x²)' / 2√( x² + 1,2² ) + ( (2,4 - x)² )' / 2√( 2² + (2,4 - x)² ) = v₀ (t)' =>

=> 2x / 2√( x² + 1,2² ) + 2(2,4 - x)(-1) / 2√( 2² + (2,4 - x)² ) = v₀ (t)' =>

=> x / √( x² + 1,2² ) - (2,4 - x) / √( 2² + (2,4 - x)² ) = v₀ (t)'

(t)' = 0 => x / √( x² + 1,2² ) - (2,4 - x) / √( 2² + (2,4 - x)² ) = 0 =>

=> x / √( x² + 1,2² ) = (2,4 - x) / √( 2² + (2,4 - x)² ) =>

=> x² ( 2² + (2,4 - x)² ) = (2,4 - x)² ( x² + 1,2² ) =>

=> x² ( 4 + 5,76 - 4,8x + x² ) = ( 5,76 - 4,8x + x²) ( x² + 1,44 ) =>

=> 9,76x² - 4,8x³ + x⁴ = 5,76x² + 8,2944 - 4,8x³ - 6,912x + x⁴ + 1,44x² =>

=> 4x² = 8,2944 - 6,912x + 1,44x² => 2,56x² + 6,912x - 8,2944 = 0 => x² + 2,7x - 3,24 = 0

Δ = 2,7² - 4 (- 3,24) = 7,29 + 12,96 = 20,25 = 4,5² x₁ = ( - 2,7 + 4,5 ) / 2 = 0,9 m δεκτή

x₂ = ( - 2,7 - 4,5 ) / 2 = - 3,6 m απορρίπτεται

για x = 0,9 m η (1) => 1,5 + 2,5 = v₀ t => t = 4 / v₀ η συνάρτηση παρουσιάζει ακρότατο ( ελάχιστο )

x = 1 m √( 1² + 1,2² ) + √( 2² + (2,4 - 1)² ) = v₀ t => 1,562 + 2,441 = v₀ t => t = 4,003 / v₀

x = 1,4 m √( 1,4² + 1,2² ) + √( 2² + (2,4 - 1,4)² ) = v₀ t => 3,4 + 5 = v₀ t => t = 8,4 / v₀

x = 0,8 m √( 0,8² + 1,2² ) + √( 2² + (2,4 - 0,8)² ) = v₀ t => 1,442 + 2,561 = v₀ t => t = 4,003 / v₀

x = 0,4 m √( 0,4² + 1,2² ) + √( 2² + (2,4 - 0,4)² ) = v₀ t => 1,265 + 8 = v₀ t => t = 9,265 / v₀

....................................................................................................................................................

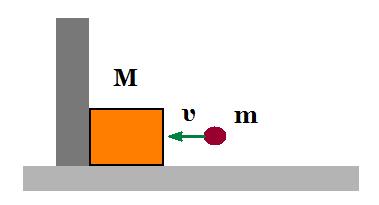
Στο σχήμα σφαίρα μάζας m που κινείται οριζόντια σφηνώνεται σε ακίνητο σώμα μάζας Μ=3m που ακουμπά σε τοίχο. Η ελάχιστη κινητική ενέργεια που απαιτείται για να σφηνωθεί όλη η σφαίρα στο ξύλο είναι Κ. Αν δεν υπάρχει τοίχος και το σώμα μάζας Μ είναι ελεύθερο να κινηθεί πάνω σε λείο οριζόντιο δάπεδο, η ελάχιστη απαιτούμενη κινητική ενέργεια ώστε το βλήμα να σφηνωθεί όλο στο σώμα είναι: α. 4Κ/3 β. 2Κ/5 γ. 3Κ

1η περίπτωση : W = 0 - K = - K (1)

K_αρχ = 0,5 m v² m v = (m + 3m) u => u = v/4

2η περίπτωση : W = K_τελ - K_αρχ = 0,5 4m (v/4)² - 0,5 m v² = 0,5 m v²/4 - 0,5 m v² = - 3/4 0,5 m v² = - 3/4 Κ_αρχ (2)

(1) , (2) => - Κ = - 3/4 Κ_αρχ => Κ_αρχ = 4/3 Κ