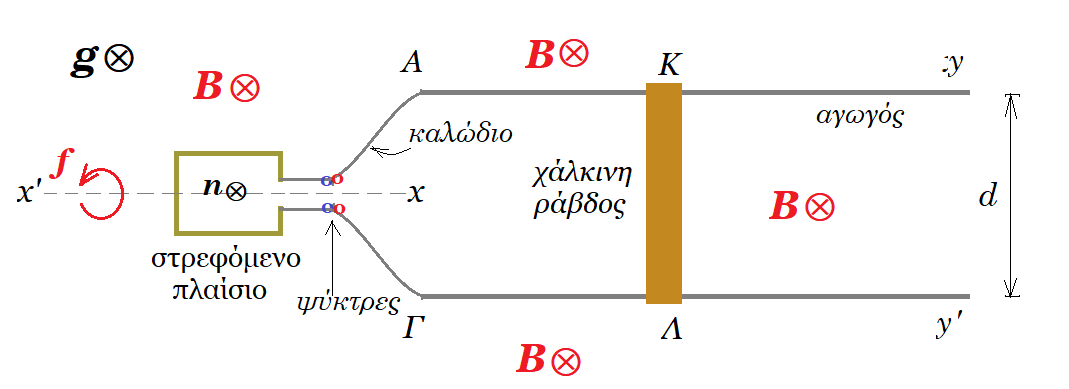

Ορθογώνιο μεταλλικό πλαίσιο έχει διαστάσεις α = 0,5 m και β = 0,2 m, αποτελείται από Ν = 100 σπείρες πολύ λεπτό σύρμα το οποίο έχει ωμική αντίσταση Rπλ. = 10 Ω. Το πλαίσιο μπορεί να περιστρέφεται γύρω από τον άξονά του x'x, ο οποίος περνά από το κέντρο του, πάνω στο επίπεδό του, με σταθερή συχνότητα f = 10 Hz, μέσα σε ομογενές μαγνητικό πεδίο έντασης Β = 0,5 Τ. Tο πλαίσιο συνδέεται μέσω ψυκτρών με καλώδια μηδενικής ωμικής αντίστασης, με παράλληλους μεταλλικούς αγωγούς Αy και Γy' μηδενικής ωμικής αντίστασης, οι οποίοι απέχουν απόσταση d=1m, επάνω στους οποίους είναι σε επαφή λεπτή χάλκινη ράβδος ΚΛ μήκους d, ωμικής αντίστασης RΚΛ = 10 Ω, μάζας m = 0,1 kg. Η ράβδος είναι κάθετη στους αγωγούς Αy και Γy' και μπορεί να κινείται χωρίς τριβές παράλληλα στον εαυτό της μέσα στο ομογενές μαγνητικό πεδίο Β κάθετα στις δυναμικές γραμμές του πεδίου. Τη χρονική στιγμή t0 = 0 η ράβδος ΚΛ είναι ακίνητη σε επαφή με τους αγωγούς Αy και Γy' σε απόσταση 0,5 m από τα σημεία Α και Γ και το πλαίσιο είναι κάθετο στις δυναμικές γραμμές του μαγνητικού πεδίου, το πλαίσιο στρέφεται με σταθερή συχνότητα f.
αρχικά τη στιγμή t0 = 0 η ράβδος ΚΛ είναι ακίνητη σε επαφή με τους αγωγούς Αy και Γy' σε απόσταση 0,5 m από τα σημεία Α και Γ και η επιφάνεια του πλαισίου είναι κάθετη στην ένταση Β, το διάνυσμα n της επιφάνειας του πλαισίου ομόρροπο B από την επιφάνεια του πλαισίου διέρχεται η μέγιστη μαγνητική ροή
Φμέγιστη = Β Α Ν = Β α β Ν = 0,5 Τ 0,5 m 0,2 m 100 σπείρες = 5 Weber
Φ = Β Α Ν συνθ = Β α β Ν συνωt = Β α β Ν συν(2πft) = 0,5 Τ 0,5 m 0,2 m 100 συν(2π 10 t) = 5 συν(20πt)
η μαγνητική ροή συναρτήσει του χρόνου δίνεται από την σχέση : Φ(t) = 5 συν(20πt) t ® sec Φ ® Weber
το πλαίσιο στρέφεται οπότε μεταβάλλεται η μαγνητική ροή που διέρχεται μέσα από την επιφάνεια του πλαισίου οπότε εμφανίζεται επαγωγική τάση στα άκρα του πλαισίου :
Εεπαγ. = - ΔΦ/Δt = - ( 5 συν(20πt) )' = - 5 20π ( - ημ(20πt) ) = 100π ημ(20πt)
έχουμε εναλλασσόμενη τάση V(t) = 100π ημ(20πt) t ® sec V ® Volt στα άκρα Α και Γ των μεταλλικών αγωγών Αy και Γy' που σημαίνει ότι εμφανίζεται εναλλασσόμενη τάση στα άκρα της χάλκινής ράβδου ΚΛ η οποία διαρρέεται από ρεύμα της μορφής : i(t) = V(t) / ( Rπλ. + RΚΛ ) = 100π ημ(20πt) / (10 + 10) = 5π ημ(20πt)
το πλάτος της τάσης είναι : V0 = 100π Volt , η ενεργός τάση είναι : Vεν = 100π / √2 Volt = 50π √2 Volt
το πλάτος της έντασης είναι : Ι0 = 5π Α , η ενεργός ένταση είναι : Ιεν = 5π / √2 Α = 2,5π √2 Α
η ράβδος ΚΛ δέχεται στο μέσον της δύναμη Laplace FL = B i d = 0,5 T 5π ημ(20πt) 1 m = 2,5π ημ(20πt)
ΣF = m a => FL = m a => 2,5π ημ(20πt) = 0,1 α => α = 25π ημ(20πt)
η ράβδος ΚΛ κινείται με επιτάχυνση μεταβαλλόμενη με τον χρόνο α(t) = 25π ημ(20πt)
η ταχύτητα της ράβδου : υ(t) = - 25π/20π συν(20πt) = - 5/4 συν(20πt)
η απομάκρυνση από τη θέση ισορροπίας : x(t) = - 5/(80π) ημ(20πt)
η ράβδος ΚΛ εκτελεί Α.Α.Τ. με πλάτος Α = 5/(80π) m = 1/(16π) m @ 0,02 m και συχνότητα f = 10π Hz
Το ορθογώνιο μεταλλικό πλαίσιο ΑΒΓΔ, με πλευρές (ΑΒ)=α=0,3m και (ΒΓ)=β=0,2m, μπορεί να περιστρέφεται γύρω από τον άξονά του x'x, ο οποίος περνά από το κέντρο του, πάνω στο επίπεδό του, με σταθερή γωνιακή ταχύτητα ω=100rad/s, μέσα σε ένα ομογενές μαγνητικό πεδίο έντασης Β=0,5Τ. Έστω t0 = 0 η στιγμή που η κάθετος στο πλαίσιο είναι παράλληλη με την ένταση του πεδίου.
A) Να βρεθεί η μαγνητική ροή που περνά από το πλαίσιο και ο ρυθμός μεταβολής της την στιγμή t0=0.
B) Να υπολογισθεί την στιγμή αυτή, η τάση στα άκρα Κ και Λ του πλαισίου, καθώς και ΗΕΔ από επαγωγή που αναπτύσσεται σε κάθε πλευρά του πλαισίου.
Γ) Ποιες οι αντίστοιχες απαντήσεις στο προηγούμενο ερώτημα την χρονική στιγμή t1=π/200s;
Φ = Β α β συν0° = 0,5 Τ 0,3 m 0,2 m = 0,03 Weber
Φ = Β α β συνφ = Β α β συνωt = 0,03 συν100t dΦ/dt = - 3 ημ100t t = 0 dΦ/dt = - 3 ημ0 = 0
Φ = 0,03 συν(100 π/200) = 0,03 0 = 0 dΦ/dt = - 3 ημ(100 π/200) = - 3 Wb/s
Με ένα σύρμα αμελητέας ωμικής αντίστασης μήκους L φτιάχνουμε ένα τετραγωνικό πλαίσιο πλευράς α που έχει Ν1 σπείρες
και συνδέουμε τα άκρα του με αντιστάτη αντίστασης R. Στρέφουμε το πλαίσιο με σταθερή γωνιακή ταχύτητα ω1 μέσα σε ομογενές
μαγνητικό πεδίο έντασης μέτρου Β, γύρω από άξονα που διέρχεται από τα μέσα των δύο απέναντι πλευρών του και είναι κάθετος στις μαγνητικές δυναμικές γραμμές. Στη συνέχεια με το ίδιο σύρμα φτιάχνουμε ένα νέο τετραγωνικό πλαίσιο πλευράς 2α και συνδέουμε τα άκρα του με αντιστάτη αντίστασης 2R. Στρέφουμε το νέο πλαίσιο με γωνιακή ταχύτητα μέτρου 2ω1 στο ίδιο ομογενές μαγνητικό πεδίο και με τον ίδιο τρόπο όπως το πρώτο. Αν P1 , P2 είναι τα σύμβολα των μέσων ισχύων που αναπτύσσονται στους αντιστάτες R και 2R αντίστοιχα, τότε αυτές συνδέονται με τη σχέση : Ρ1 / Ρ2 = 1/8 Ρ1 / Ρ2 = 1/2 Ρ1 / Ρ2 = 1/4
L = Ν1 4.α V1 = ω1 . N1 . B . α2 = ω1 . L/4.α . B . α2 = ω1 . L/4 . B . α Ρ1 = Vεν 2 / R = V1 2 / 2 R = (ω1 . L/4 . B . α)2 / 2 R = ω12 . L2 . B2 . α2 / 32.R
L = Ν2 4. 2.α V2 = 2.ω1 . N2 . B . 4α2 = 2.ω1 . L/8.α . B . 4α2 = ω1 . L . B . α Ρ2 = Vεν 2 / 2R = V2 2 / 2 2R = (ω1 . L . B . α)2 / 4R = ω12 . L2 . B2 . α2 / 4.R
Ρ1 / Ρ2 = 1/8