Ισορροπία στερεού - Ταλάντωση - Επιταχυνόμενη κίνηση
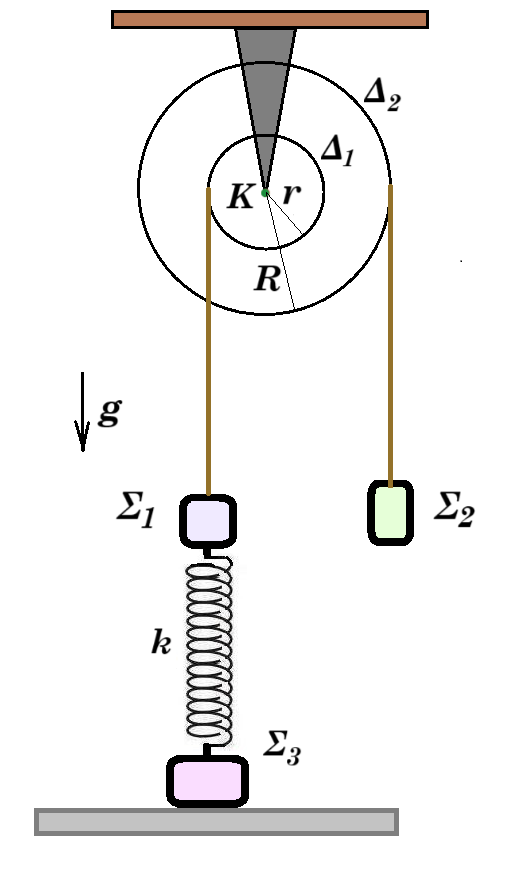
Διπλή τροχαλία μάζας Μ = 0,5 kg αποτελείται από δυο ομογενείς δίσκους συγκολλημένους κατάλληλα ώστε ο σταθερός οριζόντιος άξονας γύρω από τον οποίο μπορούν να στρέφονται σε κατακόρυφο επίπεδο χωρίς τριβές να διέρχεται από τα κέντρα μάζας τους. Ο δίσκος Δ1 έχει ακτίνα r = 0,5 m και ο δίσκος Δ2 έχει ακτίνα R = 1m.
Στους δυο δίσκους είναι τυλιγμένα αβαρή και μη εκτατά νήματα. Στο ελεύθερο άκρο του νήματος 1 που είναι τυλιγμένο στο δίσκο Δ1 είναι δεμένο σώμα Σ1 με μάζα m1 το οποίο είναι προσδεδεμένο στο πάνω άκρο κατακόρυφου ιδανικού ελατηρίου σταθεράς k = 100 N/m. Στο κάτω άκρο του ελατηρίου είναι προσδεδεμένο σώμα Σ3 μάζας m3 που είναι σε επαφή με το οριζόντιο επίπεδο. Στο ελεύθερο άκρο του νήματος 2 που είναι τυλιγμένο στον δίσκο Δ2 είναι δεμένο σώμα Σ2 με μάζα m2. Αρχικά όλα τα σώματα ισορροπούν ακίνητα και το ελατήριο έχει το φυσικό του μήκος l0. Την χρονική στιγμή t0 = 0 κόβεται το νήμα 1 με αποτέλεσμα το σώμα Σ1 να εκτελεί κατακόρυφη απλή αρμονική ταλάντωση και το Σ2 να εκτελεί ευθύγραμμη ομαλά επιταχυνόμενη κίνηση με το νήμα 2 να μην ολισθαίνει ως προς τον δίσκο Δ2. Την χρονική στιγμή t1 = 0,25√(3/2) s κάποιο σημείο της περιφέρειας του δίσκου Δ1 έχει κεντρομόλο επιτάχυνση με μέτρο ακ=3m/s2 και την χρονική στιγμή t2 = π/4 s το σώμα Σ1 διέρχεται για τρίτη φορά από την θέση ισορροπίας της ταλάντωσης που εκτελεί. Θεωρήστε τα σώματα υλικά σημεία. Δίνεται g = 10 m/s2. |
 |
Να υπολογίσετε :
1) το μέτρο της δύναμης που δέχεται η διπλή τροχαλία από τον άξονα περιστροφής της όταν το σύστημα των σωμάτων ισορροπούσε.
2) το μέτρο της επιτάχυνσης ενός σημείου της περιφέρειας του δίσκου Δ2 την χρονική στιγμή t1.
3) το μήκος του νήματος 2 που έχει ξετυλιχθεί από την χρονική στιγμή t0 έως την χρονική στιγμή t1.
4) την μάζα m3 του σώματος Σ3 αν γνωρίζετε ότι κατα την διάρκεια της ταλάντωσης του σώματος Σ1 η μέγιστη σε μέτρο δύναμη που δέχεται το σώμα Σ3 από το οριζόντιο επίπεδο έχει μέτρο |Ν|max = 40 N.
ισορροπία Σ1 : m1 g = T1 ισορροπία Σ2 : m2 g = T2 Στ(Κ) = 0 => Τ1 r = T2 R => T1 = 2 T2 m1 = 2 m2
θέση ισορροπίας Σ1 για την ταλάντωση : m1 g = k x0 => m1 10 = 100 x0 => m1 = 10 x0 συσπείρωση
Τ + Τ/4 = π/4 s => 5T/4 = π/4 s => T = π/5 s ω = 2π/Τ = 2π / π/5 = 10 rad/s
k = m1 ω2 => 100 = m1 102 => m1 = 1 kg m2 = 0,5 kg
x0 = m1 / 10 = 1/10 = 0,1 m = x0 πλάτος ταλάντωσης Σ1
η τροχαλία δέχεται δυνάμεις : FK - Mg - T1 - T2 = 0 => FK - 5 - 10 - 5 = 0 => FK = 20 N
ak1 = v12 / r => 3 m/s2 = v12 / 0,5 m => v12 = 3/2 => v1 = √(3/2) m/s γραμμική ταχύτητα
v1 = a1 t1 => √(3/2) = a1 0,25√(3/2) => a1 = 4 m/s2 επιτάχυνση Σ1 και κάποιου σημείου της περιφέρειας του Δ1 επιτρόχια επιτάχυνση
α1 = αγων r α2 = αγων R = αγων 2r = 2 a1 = 8 m/s2 επιτρόχια
α1 = αγων r => 4 m/s2 = αγων 0,5 m => αγων = 8 rad/s2
ω = αγων t1 = 8 rad/s2 0,25√(3/2) s = 2 √(3/2) = √6 rad/s v2 = ω R = √6 rad/s 1 m = √6 m/s επιτράχια ταχύτητα
κεντρομόλος επιτάχυνση : ak2 = v22 / R = 6 / 1 = 6 m/s2
συνολική επιτάχυνση : α22 + ακ22 = 82 + 62 = 102 => α = 10 m/s2
l = 0,5 a2 t12 = 0,5 8 m/s2 ( 0,25√(3/2) s )2 = 4 m/s2 1/16 3/2 s2 => l = 3/8 m
μέγιστη δύναμη από το οριζόντιο επίπεδο δέχεται το Σ3 όταν το ελατήριο είναι συσπειρωμένο ( η δύναμη ελατηρίου είναι ομόρροπη του βάρους Σ3 ) δηλαδή το Σ1 εκείνη τη στιγμή βρίσκεται στο κάτω άκρο της ταλάντωσής του x0 = 0,1 m οπότε το ελατήριο έχει συσπείρωση 2x0 = 0,2 m οοπότε Nmax = m3 g + k 2x0 => 40 = m3 10 + 100 0,2 => m3 = 2 kg
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Σώμα Σ₁ μάζας m₁ βρίσκεται πάνω σε λείο οριζόντιο επίπεδο και στο πάνω μέρος του έρχεται σε επαφή με λεπτή ομογενή ράβδο (ΟΓ) μάζας Μ = 5 kg με την οποία εμφανίζει τριβή. Η διεύθυνση της ράβδου σχηματίζει γωνία φ = 45⁰ με την κατακόρυφο και η ράβδος μπορεί να περιστρέφεται σε κατακόρυφο επίπεδο γύρω από ακλόνητο οριζόντιο άξονα που διέρχεται από το άκρο της Ο. Το σώμα Σ₁ είναι δεμένο με οριζόντιο αβαρές και μη εκτατό νήμα (1) που είναι τυλιγμένο στον δίσκο (1) τροχαλίας που αποτελείται από δυο δίσκους ακτίνων R₁ = 2R και R₂ = R οι οποίοι είναι συγκολλημένοι κατα τέτοιο τρόπο ώστε ο σταθερός άξονας της τροχαλίας να διέρχεται από το κοινό τους κέντρο όπως φαίνεται στο σχήμα. 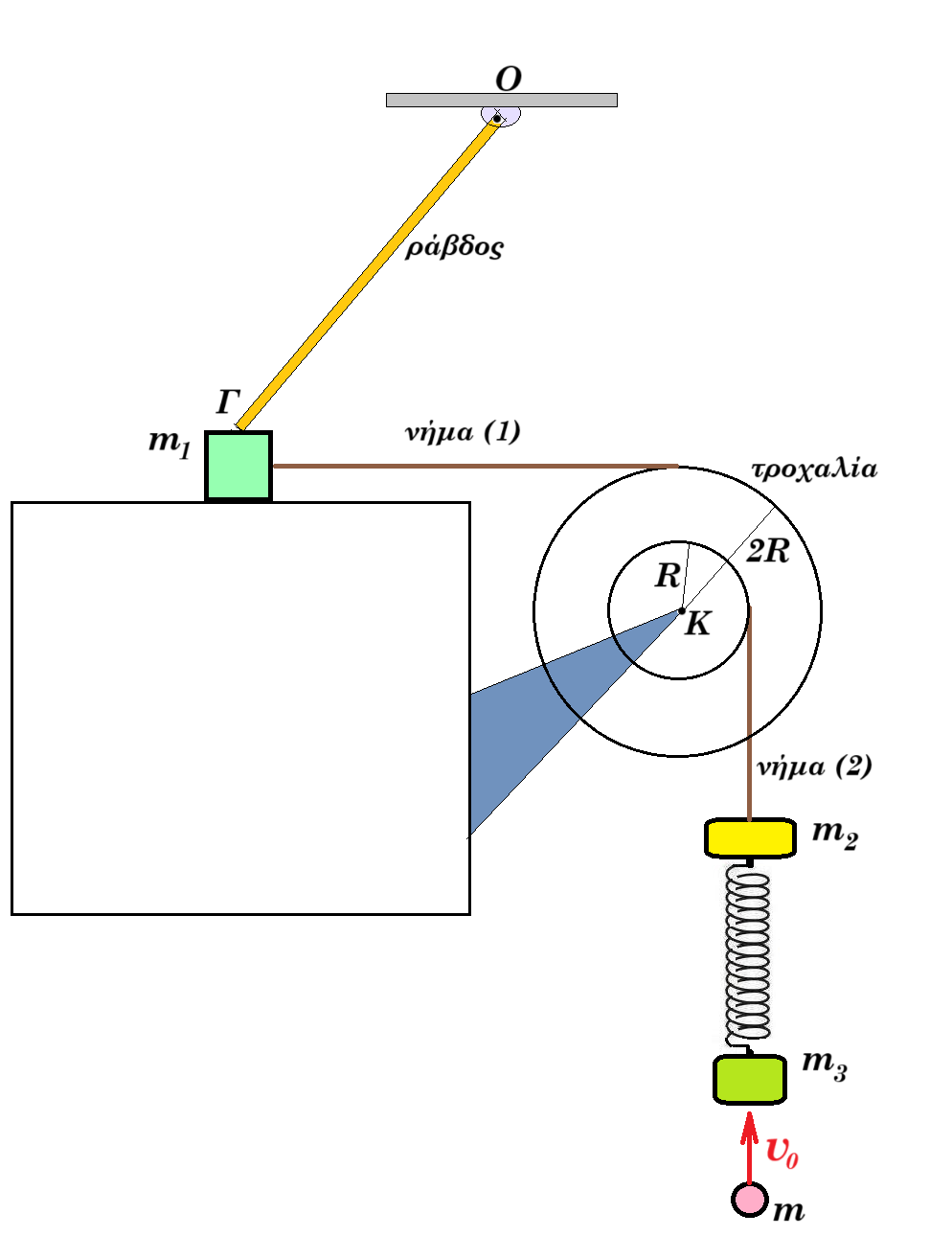 Στον δίσκο (2) είναι τυλιγμένο αβαρές και μη εκτατό κατακόρυφο νήμα (2) που το ελεύθερο άκρο του είναι δεμένο σε σώμα Σ₂ με μάζα m₂ = 1 kg. Στο κάτω μέρος του Σ₂ είναι δεμένο ιδανικό κατακόρυφο ελατήριο σταθεράς k = 100 N/m που στο κάτω του άκρο έχει δεμένο σώμα Σ₃ με μάζα m₃ = 3 kg. Αρχικά όλα τα σώματα του συστήματος ισορροπούν ακίνητα. Την χρονική στιγμή t₀ = 0 βλήμα μάζας m = 1 kg με κατακόρυφη ταχύτητα μέτρου υ₀ και φοράς προς τα πάνω συγκρούεται
Στον δίσκο (2) είναι τυλιγμένο αβαρές και μη εκτατό κατακόρυφο νήμα (2) που το ελεύθερο άκρο του είναι δεμένο σε σώμα Σ₂ με μάζα m₂ = 1 kg. Στο κάτω μέρος του Σ₂ είναι δεμένο ιδανικό κατακόρυφο ελατήριο σταθεράς k = 100 N/m που στο κάτω του άκρο έχει δεμένο σώμα Σ₃ με μάζα m₃ = 3 kg. Αρχικά όλα τα σώματα του συστήματος ισορροπούν ακίνητα. Την χρονική στιγμή t₀ = 0 βλήμα μάζας m = 1 kg με κατακόρυφη ταχύτητα μέτρου υ₀ και φοράς προς τα πάνω συγκρούεται
πλαστικά με το Σ₃ με αποτέλεσμα το συσσωμάτωμα που δημιουργείται να εκτελεί απλή αρμονική ταλάντωση στην διάρκεια της οποίας το Σ₂ παραμένει ακίνητο και υπάρχουν χρονικές στιγμές που το νήμα (2) είναι οριακά τεντωμένο. Μεταξύ ράβδου, τροχαλίας και των αξόνων περιστροφής τους δεν εμφανίζονται τριβές και όλα τα σώματα βρίσκονται
στο ίδιο κατακόρυφο επίπεδο.
Δίνεται g = 10 m/s² και ημ45⁰ = συν45⁰.
Να υπολογίσετε :
1) το μέτρο της δύναμης που δέχεται η ράβδος από τον άξονα περιστροφής της πριν την χρονική στιγμή t₀ = 0.
2) το πλάτος ταλάντωσης του συσσωματώματος που δημιουργείται.
3) το μέτρο της ταχύτητας υ₀ του βλήματος ακριβώς πριν την δημιουργία του συσσωματώματος.
4) την ελάχιστη τιμή του συντελεστή στατικής τριβής μεταξύ ράβδου και σώματος Σ₁ ώστε να μην ολισθήσει το ένα σώμα σε σχέση με το άλλο.
Θεωρήστε θετική κατεύθυνση την κατακόρυφη προς τα πάνω
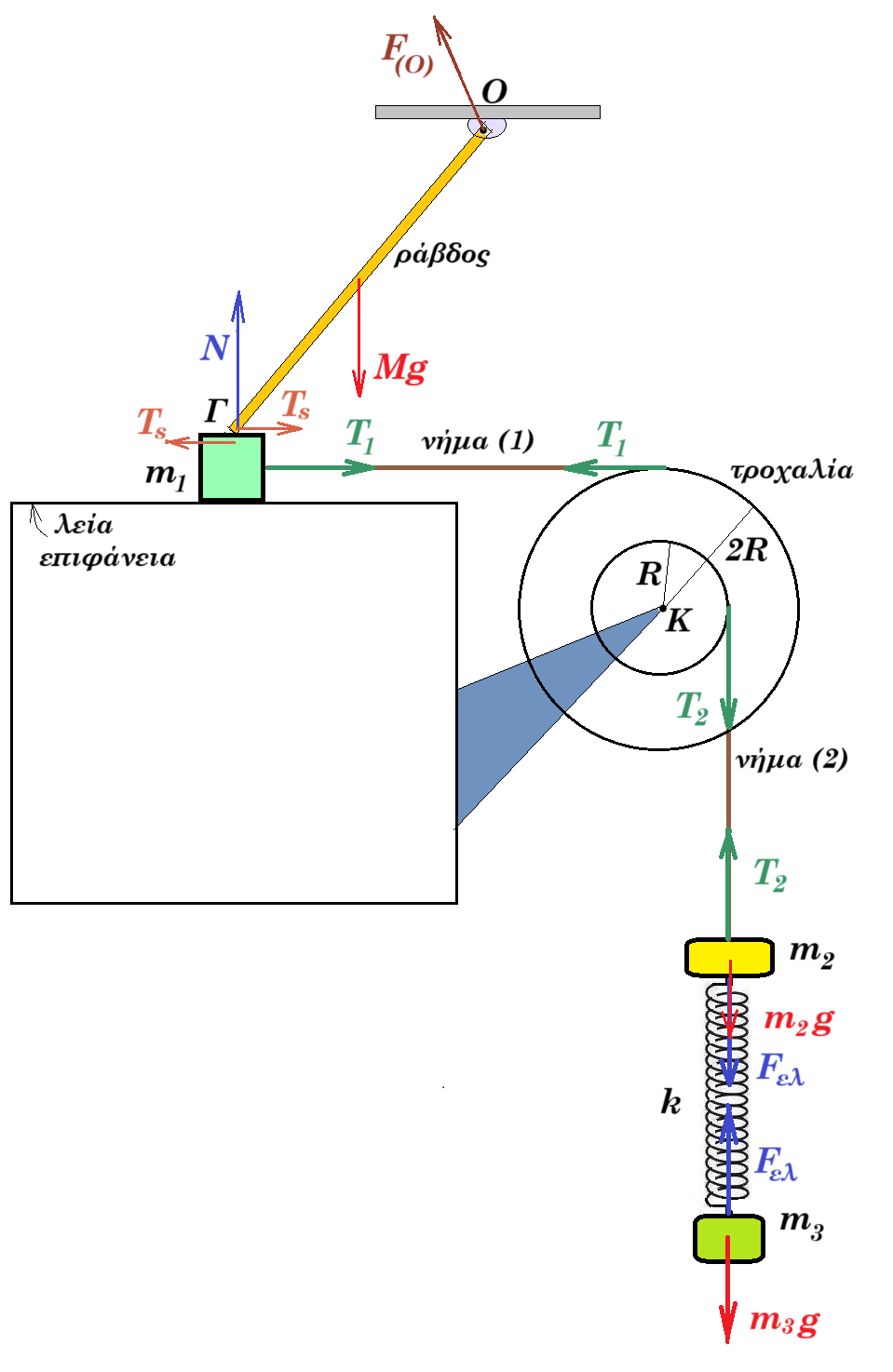
(A) ισορροπία Σ3 : m3 g = k Δl => 30 = 100 Δl => Δl = 0,3 m επιμήκυνση ελατηρίου
ισορροπία Σ2 : Τ2 - m2 g - k Δl = 0 => Τ2 - 10 - 30 = 0 => Τ2 = 40 Ν προς τα πάνω
ισορροπία τροχαλίας : Στ(Κ) = 0 => Τ2 R = T1 2R => T1 = 20 N
ισορροπία Σ1 : ΣFx = 0 => Τs = T1 = 20 N
ισορροπία ράβδου : Στ(Ο) = 0 => Mg l/2 ημ45° + Τs l συν45° - Ν l ημ45° = 0 =>
=> Mg 1/2 + Τs - Ν = 0 => 50 1/2 + 20 - Ν = 0 => Ν = 45 Ν
ΣFy = 0 => N - Mg + F(O),y = 0 => 45 - 50 + F(O),y = 0 => F(O),y = 5 N προς τα πάνω
ΣFx = 0 => Ts + F(O),x = 0 => 20 + F(O),x = 0 => F(O),x = - 20 N οριζόντια αριστερά
F(O)2 = F(O),x2 + F(O),y2 = 202 + 52 = 425 => F(O) = 5√17 N
πλαστική κρούση : m v0 = (m3 + m) v => 1 v0 = 4 v
ισορροπία σφαίρας-Σ3 : (m3 + m) g = k Δl' => 40 = 100 Δl' => Δl' = 0,4 m επιμήκυνση ελατηρίου k = (m3 + m) ω2 => 100 = 4 ω2 => ω = 5 rad/s
το συσσωμάτωμα αμέσως μετά την κρούση είναι σε θέση Δl' - Δl = 0,1 m υψηλότερα από την θέση ισορροπίας του και έχει ταχύτητα v = v0 / 4
x = A ημ(5t) υ = 5A συν(5t) α = - 25A ημ(5t)
ΣF = (m3 + m) a = 4 [ - 25A ημ(5t) ] => ΣF = - 100A ημ(5t)
Fελ - (m3 + m) g = - 100A ημ(5t) => Fελ = 40 - 100A ημ(5t) ή 40 - 100.x
το Σ2 δέχεται από το ελατήριο Fελ' = - 40 + 100.x
ισορροπία Σ2 : Τ2 - m2 g + Fελ' = 0 => Τ2 - 10 - 40 + 100.x = 0 => Τ2 = 50 - 100.x
οριακά τεταμένο νήμα : T2 ³ 0 => 50 - 100.x ³ 0 => x £ 0,5 m πλάτος της ΑΑΤ : Α = 0,5 m
το συσσωμάτωμα αμέσως μετά την κρούση είναι σε θέση Δl' - Δl = 0,1 m υψηλότερα από την θέση ισορροπίας του και έχει ταχύτητα v = v0 / 4
0,5 (m3 + m) v2 + 0,5 k 0,12 = 0,5 k A2 => 4 v2 + 100 0,01 = 100 0,52 =>
=> 4 v2 = 25 - 1 => v = √6 m/s v0 = 4√6 m/s
Τ2 = 50 - 100.x => T1 = 25 - 50.x = Ts [- 0,5 m , + 0,5 m]
x = - 0,5 m => Ts = 50 N x = 0 => Ts = 25 N x = + 0,5 m => Ts = 0
ισορροπία ράβδου : Στ(Ο) = 0 => Mg l/2 ημ45° + Τs l συν45° - Ν l ημ45° = 0 =>
=> Mg 1/2 + Τs - Ν = 0 => 50 1/2 + 25 - 50.x - Ν = 0 =>
=> Ν = 50 - 50.x [- 0,5 m , + 0,5 m]
x = - 0,5 m => Ν = 75 N x = 0 => Ν = 50 N x = + 0,5 m => Ν = 25 Ν
μ = Τs / Ν = 50 / 75 = 2/3
 |
Ομογενής ράβδος ΑΟ μάζας Μ = 2m και μήκους L έχει το άκρο της Ο αρθρωμένο σε κατακόρυφο τοίχο. Η διεύθυνση της ράβδου σχηματίζει γωνία φ με τον τοίχο και δεν εμφανίζονται τριβές στην άρθρωση. Στο μέσο Κ της ράβδου είναι δεμένο το ένα άκρο ιδανικού νήματος που έχει διεύθυνση κάθετη στην ράβδο ενώ το άλλο άκρο του νήματος είναι στερεωμένο στον κατακόρυφο τοίχο. Στο άκρο Α της ράβδου είναι προσδεδεμένο το ένα άκρο ιδανικού κατακόρυφου ελατηρίου σταθεράς k που στο κάτω άκρο του είναι δεμένο σώμα Σ μάζας m που εκτελεί κατακόρυφη απλή αρμονική ταλάντωση. Αρχικά η διάταξη είναι σε ισορροπία. Μετακινούμε το σώμα Σ κατακόρυφα προς τα πάνω ώστε το ελατήριο να έχει το φυσικό του μήκος. Τη στιγμή μηδέν αφήνουμε το σώμα να κινηθεί. Θετική κατεύθυνση προς τα πάνω.
Εκφράστε την δύναμη που ασκείται στο μέσον Κ της ράβδου από το νήμα συναρτήσει του χρόνου t και συναρτήσει της απομάκρυνσης x του σώματος Σ από τη θέση ισορροπίας του.
m = 1 kg g = 10 m/s2 L = 1 m k = 100 N/m ημφ = 0,8
|
 |
ισορροπία σώματος Σ : mg = k Δl => Δl = 10/100 = 0,1 m επιμήκυνση (-)
k = m ω2 => 100 = 1 ω2 => ω = 10 rad/s
το Σ εκτελεί ΑΑΤ με πλάτος Δl : x(t) = 0,1 ημ(10.t + π/2)
v(t) = 1 συν(10.t + π/2) α(t) = - 10 ημ(10.t + π/2)
ΣF = m a => Fελατ - mg = m a => Fελατ(t) = 10 - 10 ημ(10.t + π/2)
Fελατ(x) = 10 - 100.x = - k (x + Δl) Δl = - 0,1m [ -0,1m , +0,1m ]
στο άκρο Α της ράβδου ασκείται η δύναμη F ' = - Fελατ(x) = - 10 + 100.x
x = - 0,1 m F ' = - 20 N x = + 0,1 m F ' = 0 συνεπώς η F ' είναι κατακόρυφη προς τα κάτω όπως το βάρος της ράβδου
Στ(Ο) = 0 => - F ' lημφ + Mg l/2 ημφ - Τ l/2 = 0 =>
=> - (- 10 + 100.x) 1 0,8 + 20 1/2 0,8 - Τ 1/2 = 0 =>
=> T(x) = 32 - 160.x [-0,1m , +0,1m] T(t) = 32 - 16 ημ(10.t + π/2)
x = - 0,1 m F ' = - 10 + 100 (-0,1) = - 20N Fελατ = 10 - 100 (-0,1) = +20N
- (- 20 ) 1 0,8 + 20 0,5 0,8 = 16 + 8 = 24 = T 0,5 => T = 48 N
x = + 0,1 m F ' = - 10 + 100 (+0,1) = 0 Fελατ = 10 - 100 (+0,1) = 0
20 0,5 0,8 = 8 = T 0,5 => T = 16 N
x = 0 F ' = - 10 N Fελατ = +10N
- (- 10 ) 1 0,8 + 20 0,5 0,8 = 8 + 8 = 16 = T 0,5 => T = 32 N
οριζόντια συνιστώσα Τx = T συνφ = (32 - 160.x) 0,6 = 19,2 - 96.x
κατακόρυφη συνιστώσα Τy = T ημφ = (32 - 160.x) 0,8 = 25,6 - 128.x
F(O),x = - Tx = - 19,2 + 96.x
F(O),y = - Ty + Mg - F ' = - (25,6 - 128.x) + 20 + 10 - 100.x = 28.x + 4,4
|
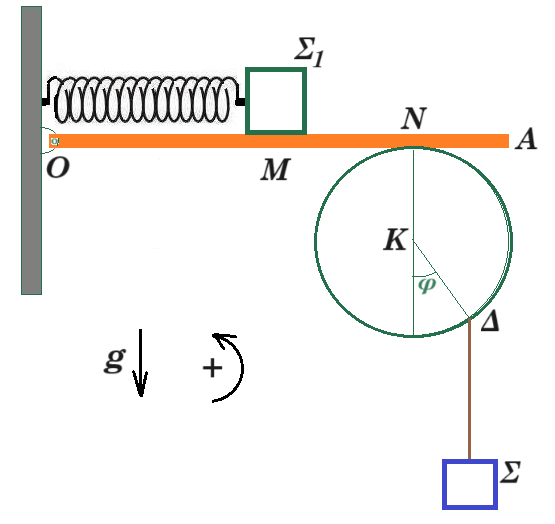
Ομογενής, λεπτή ράβδος ΟΑ μήκους L = 1m και μάζας Μ = 6 kg έχει το άκρο της Ο αρθρωμένο σε κατακόρυφο τοίχο χωρίς να αναπτύσονται τριβές. Κάτω ακριβώς από την ράβδο και σε επαφή με αυτήν στο σημείο Ν βρίσκεται δίσκος ακτίνας R ο οποίος μπορεί να στρέφεται γύρω από οριζόντιο άξονα που διέρχεται από το κέντρο του Κ χωρίς να αναπτύσσονται τριβές. Η απόσταση ΟΝ ισούται με d = 0,75 m. Σε σημείο Δ του δίσκου είναι δεμένο κατακόρυφο αβαρές και μη εκτατό νήμα που στο άλλο του άκρο είναι δεμένο σώμα Σ μάζας m = 2 kg και το ευθύγραμμο τμήμα ΚΔ σχηματίζει γωνία φ = 30⁰ με την κατακόρυφο. Ιδανικό, οριζόντιο ελατήριο σταθεράς k έχει το αριστερό του άκρο στερεωμένο στον κατακόρυφο τοίχο και στο δεξί στου άκρο είναι δεμένο σώμα Σ₁ μάζας m₁ = 3 kg το οποίο εκτελεί απλή αρμονική ταλάντωση πάνω στην ράβδο πλάτους Α = 0,25 m. H θέση ισορροπίας του σώματος Σ₁ συμπίπτει με το μέσο M της ράβδου. Μεταξύ της ράβδου και του δίσκου αναπτύσσεται στατική τριβή με αποτέλεσμα το σώμα Σ να παραμένει συνεχώς ακίνητο. Όλα τα σώματα βρίσκονται στο ίδιο κατακόρυφο επίπεδο. Δίνεται g = 10 m/s².
Να υπολογίσετε την ελάχιστη τιμή του συντελεστή στατικής τριβής μεταξύ ράβδου και δίσκου ώστε το σώμα Σ να παραμένει συνεχώς ακίνητο.
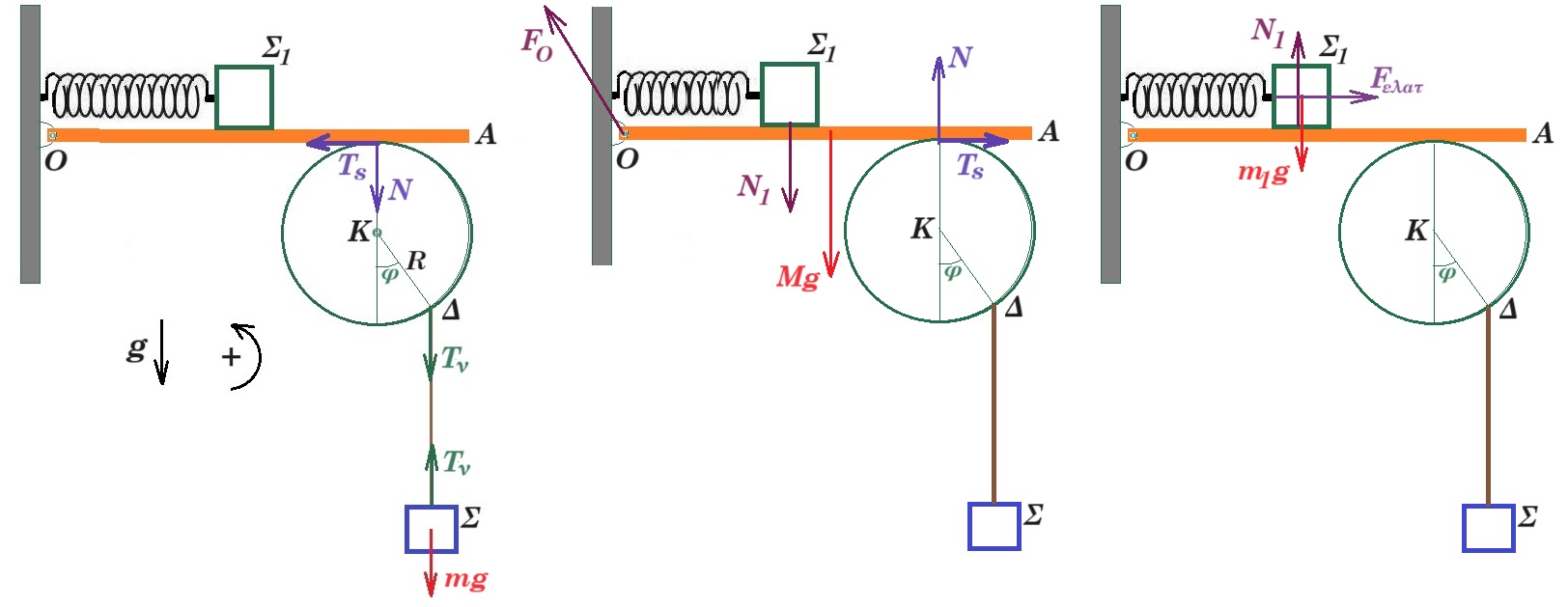
ισορροπία Σ : Tν = mg = 20 Ν
ισορροπία δίσκου : Στ(Κ) = 0 => Ts R - Tν R ημ30° = 0 => Ts = Tν = 10 N μs ³ Ts / N
Α.Α.Τ. Σ1 : ΣFy = 0 => Ν1 = m1g = 30 N ΣFx = m1 a => - k x = m1 a => - k x = - 3 ω2 x
ισορροπία ράβδου ΟΑ : Στ(Ο) = 0 => - Mg L/2 - N1 (L/2 + x) + N 3L/4 = 0 => - 30 - 30 (0,5 + x) + N 0,75 = 0 =>
=> N 0,75 = 45 + 30 x => N = 60 + 40 x επειδή - 0,25 m £ x £ + 0,25 m τότε 50 Ν £ Ν £ 70 Ν
N = 50 N μs ³ Ts / N = 10 / 50 = 0,2 N = 70 N μs ³ Ts / N = 10 / 70 = 0,14
συνολικά μs ³ 0,2 διότι
εάν Ν = 50 Ν και μs = 0,1 < 0,14 = 1/7 τότε Ts = μs N = 0,1 50 Ν = 5 Ν οπότε Στ(Κ) = Ts R - Tν R ημ30° = ( 5 - 20 ½ ) R = - 5 R διάφορο του μηδενός οπότε ο δίσκος θα περιστραφεί περί τον άξονά του όπως οι δείκτες του ρολογιού και το σώμα Σ θα κινηθεί επιταχυνόμενο προς τα κάτω
εάν Ν = 70 Ν και μs = 0,1 < 0,14 = 1/7 τότε Ts = μs N = 0,1 70 Ν = 7 Ν οπότε Στ(Κ) = Ts R - Tν R ημ30° = ( 7 - 20 ½ ) R = - 3 R διάφορο του μηδενός οπότε ο δίσκος θα περιστραφεί περί τον άξονά του όπως οι δείκτες του ρολογιού και το σώμα Σ θα κινηθεί επιταχυνόμενο προς τα κάτω
εάν Ν = 50 Ν και μs = 0,17 > 0,14 = 1/7 αλλά < 0,2 τότε Ts = μs N = 0,17 50 Ν = 8,5 Ν οπότε Στ(Κ) = Ts R - Tν R ημ30° = ( 8,5 - 20 ½ ) R = - 1,5 R διάφορο του μηδενός οπότε ο δίσκος θα περιστραφεί περί τον άξονά του όπως οι δείκτες του ρολογιού και το σώμα Σ θα κινηθεί επιταχυνόμενο προς τα κάτω
εάν Ν =70 Ν και μs = 0,17 > 0,14 = 1/7 αλλά < 0,2 τότε Ts = μs N = 0,17 70 Ν = 11,9 Ν οπότε Στ(Κ) = Ts R - Tν R ημ30° = ( 11,9 - 20 ½ ) R = 1,9 R διάφορο του μηδενός αλλά ο δίσκος δεν θα περιστραφεί διότι η στατική τριβή κάνει ροπή μεγαλύτερη της ροπής της τάσης του νήματος και ο δίσκος θα μείνει ακίνητος
εάν Ν = 50 Ν και μs = 0,3 > 0,2 = 1/5 τότε Ts = μs N = 0,3 50 Ν = 15 Ν οπότε Στ(Κ) = Ts R - Tν R ημ30° = ( 15 - 20 ½ ) R = 5 R διάφορο του μηδενός αλλά ο δίσκος δεν θα περιστραφεί διότι η στατική τριβή κάνει ροπή μεγαλύτερη της ροπής της τάσης του νήματος και ο δίσκος θα μείνει ακίνητος
εάν Ν = 70 Ν και μs = 0,3 > 0,2 = 1/5 τότε Ts = μs N = 0,3 70 Ν = 21 Ν οπότε Στ(Κ) = Ts R - Tν R ημ30° = ( 21 - 20 ½ ) R = 11 R διάφορο του μηδενός αλλά ο δίσκος δεν θα περιστραφεί διότι η στατική τριβή κάνει ροπή μεγαλύτερη της ροπής της τάσης του νήματος και ο δίσκος θα μείνει ακίνητος
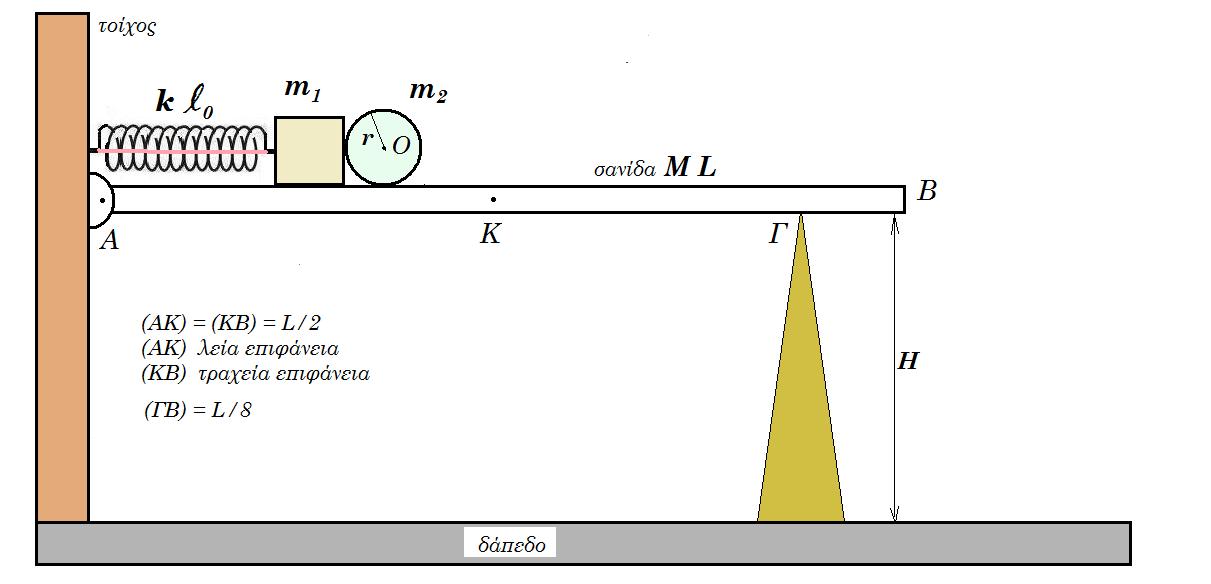
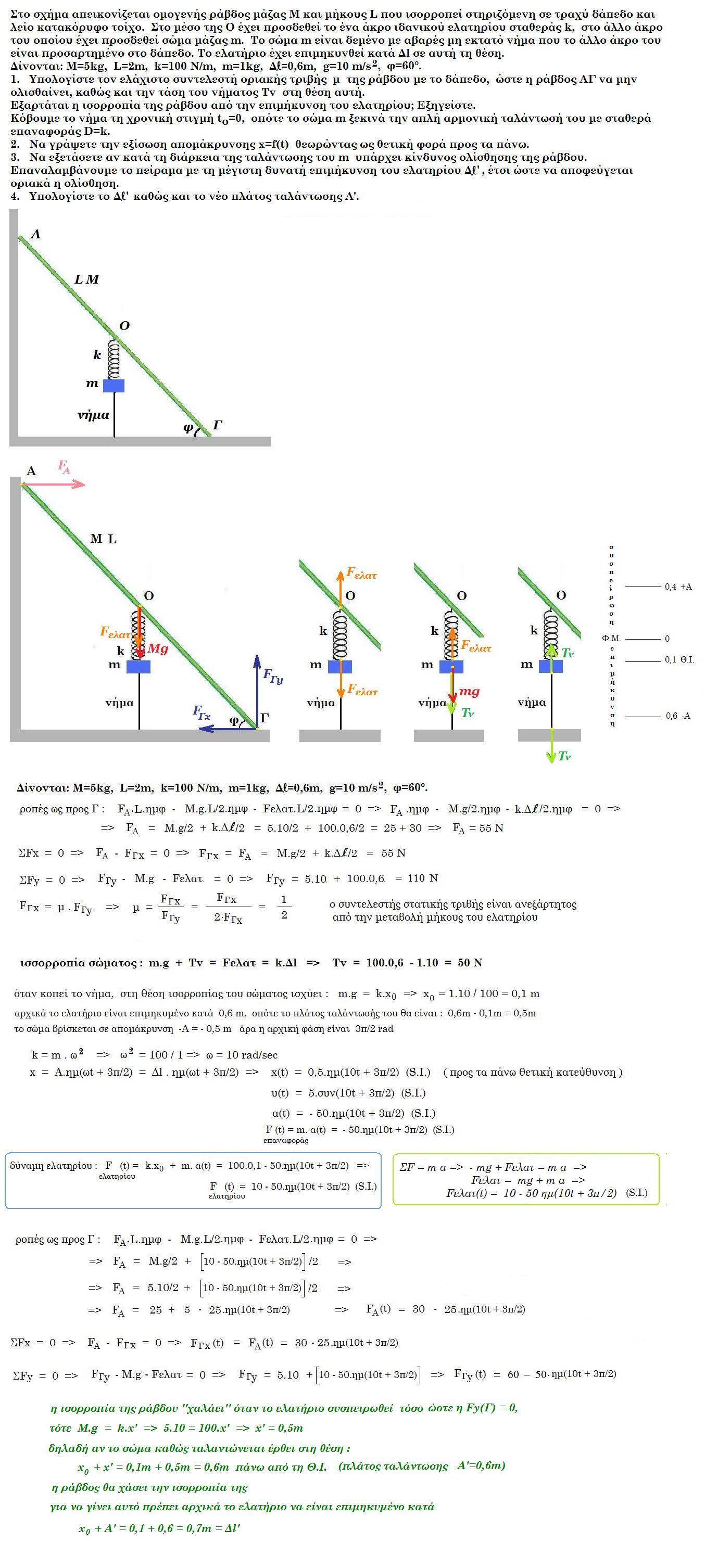
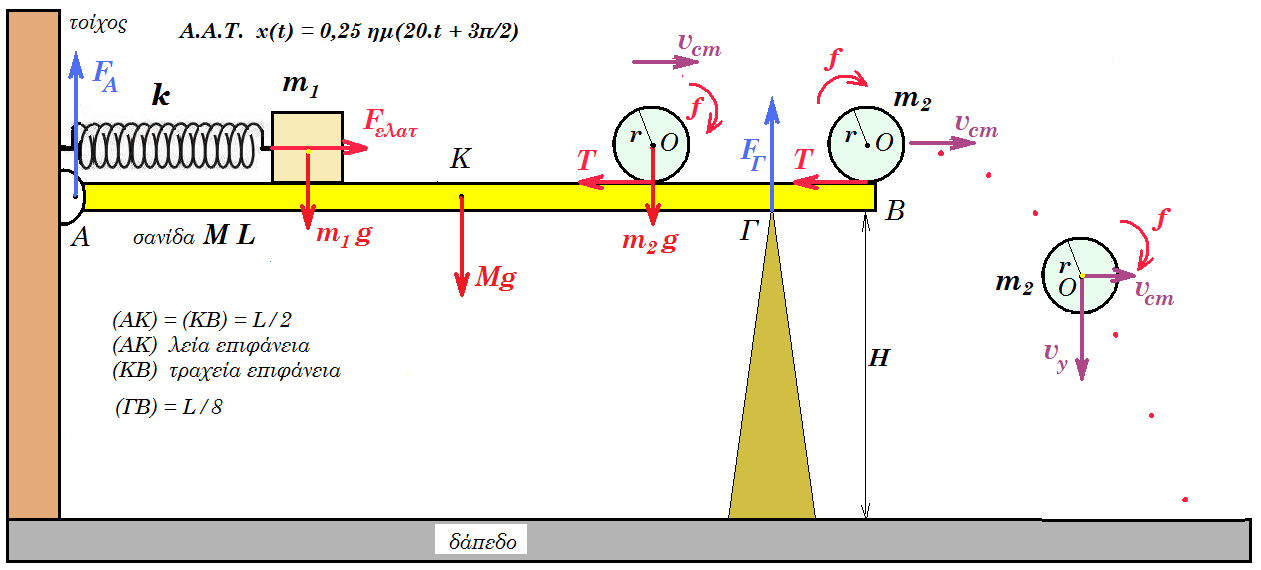
Στη διάταξη του σχήματος το ιδανικό ελατήριο σταθεράς k = 800 N/m φυσικού μήκους l0 = 0,5 m συνδέεται σε κατακόρυφο τοίχο με το ένα άκρο ενώ στο άλλο άκρο συνδέεται με σώμα Σ1 μάζας m1 = 2 kg το οποίο είναι σε επαφή με στεφάνη Σ2 μάζας m2 = 0,5 kg ακτίνας r = 0,1 m. Η λεπτή σανίδα ΑΒ έχει μάζα Μ = 4 kg μήκος L = 2 m, είναι σε οριζόντια θέση, στο άκρο Α υπάρχει άρθρωση με τον τοίχο, στο σημείο Γ υπάρχει στήριγμα (ΓΒ) = L/8. Από το άκρο της Α μέχρι το μέσον της Κ η επιφάνειά της είναι λεία ενώ από το μέσον Κ μέχρι το άκρο Β είναι τραχεία με συντελεστή μ = 0,1. Το άκρο Β της σανίδας απέχει από το δάπεδο ύψος Η = 10 m. Τα άκρα του ελατηρίου συνδέονται με λεπτό αβαρές νήμα έτσι ώστε να είναι συσπειρωμένο. Στο ελατήριο έχει αποθηκευθεί ενέργεια 25 J. Τη στιγμή t0 = 0 κόβουμε το νήμα.
(α) Μελετήστε την κίνηση των σωμάτων Σ1 και Σ2.
(β) Βρείτε την δύναμη που δέχεται η σανίδα στα σημεία Α και Γ συναρτήσει του χρόνου.
η αποθηκευμένη ενέργεια του συσπειρωμένου ελατηρίου γίνεται κινητική ενέργεια των δύο σωμάτων όταν αυτό αποκτήσει το φυσικό του μήκος
25 J = ½ k Δl2 = ½ (m1 + m2) v02
Δl2 = 2 25 J / 800 N/m = 25/400 = ( 5/20 )2 = ( 1/4 )2 => Δl = 0,25 m = 1/4 m αρχική συσπείρωση του ελατηρίου
v02 = 2 25 J / 2,5 kg = 20 => v0 = 2√5 m/s
τα σώματα αρχίζουν να κινούνται προς τα δεξιά το ελατήριο σπρώχνει τα σώματα με δύναμη Fελατ = k x προς τα δεξιά, όταν το ελατήριο αποκτήσει το φυσικό του μήκος τα σώματα έχουν ταχύτητα v0 = 2√5 m/s αλλά το Σ1 δέχεται από το ελατήριο δύναμη Fελατ = k x προς τα αριστερά διότι το ελατήριο επιμηκύνεται οπότε επιβραδύνεται ενώ το Σ2 συνεχίζει με ταχύτητα v0 = 2√5 m/s προς τα δεξιά
το Σ1 θα εκτελέσει Α.Α.Τ. με πλάτος Δl = 0,25 m συχνότητα ω2 = k / m1 = 800 / 2 => ω = 20 rad/s f = ω / 2π = 10/π Hz T = 1/f = π/10 s διότι η επιφάνεια της σανίδας είναι λεία μέχρι το μέσον της Κ
το Σ2 μέχρι το μέσον Κ της σανίδας ολισθαίνει με σταθερή ταχύτητα v0 = 2√5 m/s προς τα δεξιά ενώ από το σημείο Κ μέχρι το άκρο Β κυλίεται ω = v0 / r = 2√5 m/s / 0,1 m = 20√5 rad/s
Α είναι το σημείο επαφής της σφαίρας με το οριζόντιο επίπεδο υΑ = υcm - ω r
ολίσθση ( ευθύγραμμη ομαλά επιβραδυνόμενη κίνηση ) υcm = υ0 - αcm t x = υ0 t - ½ acm t2
T = m2 acm => μ Ν = m2 acm => μ m2 g = m2 acm => μ g = acm (1)
κύλιση ( ομαλά επιταχυνόμενη ) ω = αγων t θ = ½ αγων t2
Στ(Ο) = Ι αγων => T r = m2 r2 αγων => T = m2 r αγων => μ m2 g = m2 r αγων => μ g = r αγων (2)
(1) , (2) => acm = r αγων => vcm = r ω η στεφάνη κυλίεται χωρίς να ολισθαίνει
υΑ = υcm - ω r => 0 = υ0 - αcm t - αγων t r => t = v0 / 2acm = v0/2μg => t = 2√5 / 2.0,1.10 => t = √5 s
x = υ0 t - ½ acm t2 => x = 2√5 √5 - ½ 1 5 => x = 7,5 m 
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~

Λεπτή ομογενής ράβδος AΓ μήκους l και μάζας Μ έχει σταθερή διατομή και ισορροπεί χωρίς τριβές σε δύο στηρίγματα Γ και Δ που οι αποστάσεις τους από τα άκρα Α και Β είναι ΑΓ = ΒΔ = l/4. Στο άκρο B της ράβδου έχουμε στερεώσει το άνω άκρο ενός κατακόρυφου ελατηρίου σταθεράς k και στο κάτω άκρο του ελατηρίου έχουμε συνδέσει σώμα Σ μάζας m = Μ⁄3 το οποίο ισορροπεί. Διεγείρουμε το σύστημα (k, m) ώστε το Σ να κάνει απλή αρμονική ταλάντωση πλάτους Α.
(α) Βρείτε την μέγιστη τιμή του πλάτους Αmax ώστε η ράβδος να είναι συνέχεια ακίνητη.
(β) Πόση δύναμη δέχεται η ράβδος στα στηρίγματα στην περίπτωση αυτή;
το σώμα Σ ισορροπεί : mg = k Δl => Δl = mg/k = Mg/3k
x(t) = A ημ(ωt + π/2) υ(t) = ωA συν(ωt + π/2) α(t) = - ω2A ημ(ωt + π/2)
ΣF = m a => mg + Fελατ = - m ω2A ημ(ωt + π/2) =>
=> Fελατ = - mg - m ω2A ημ(ωt + π/2) = - mg - kx = - Mg/3 - kx => Fελατ = - Mg/3 - kx
F'ελατ = Mg/3 + kx
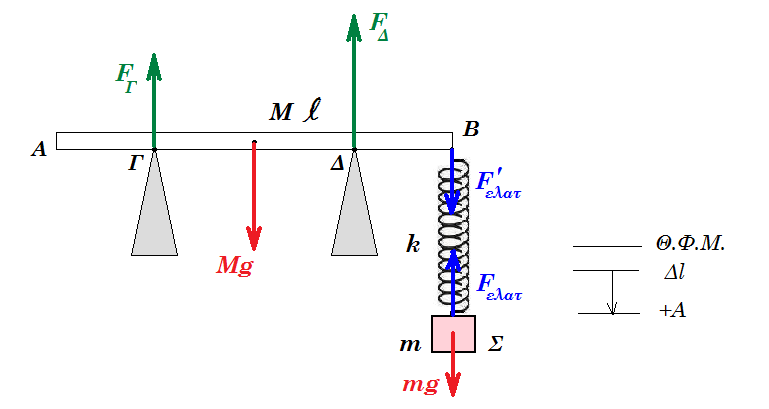
οι δυνάμεις όπως στο σχήμα το ελατήριο επιμηκυμένο άρα η F'ελατ προς τα κάτω για να μήν έχουμε ανατροπή : FΓ ³ 0
ροπές ως προς Δ : Στ(Δ) = 0 => + Mg l/4 - F'ελατ l/4 - FΓ l/2 = 0 =>FΓ = 0
=> Mg l/4 - ( Mg/3 + kA ) l/4 = 0 => Mg = Mg/3 + kA => Α = 2Mg/3k
F'ελατ = Mg/3 + kΑ = Mg/3 + 2Mg/3 = Mg
ΣF = 0 => + Mg + F'ελατ - FΓ - FΔ = 0 => + Mg + Mg - 0 - FΔ = 0 => FΔ = 2Mg

εάν το ελατήριο συσπειρωμένο άρα η F'ελατ προς τα επάνω ( F'ελατ = - Mg/3 - kx ) για να μήν έχουμε ανατροπή : FΔ ³ 0
ροπές ως προς Γ : Στ(Γ) = 0 => - Mg l/4 + F'ελατ 3l/4 + FΔ l/2 = 0 =>FΔ = 0
=> - Mg l/4 + ( - Mg/3 - kA ) 3l/4 = 0 => Mg = 3 ( - Mg/3 - kA ) =>
=> Mg = - Mg - 3kA => Α = -2Mg/3k
F'ελατ = - Mg/3 - kΑ = - Mg/3 - 2Mg/3 = - Mg
ΣF = 0 => + Mg - F'ελατ - FΓ - FΔ = 0 => + Mg - (- Mg) - FΓ - 0 = 0 => FΓ = 2Mg
σχήμα (α)
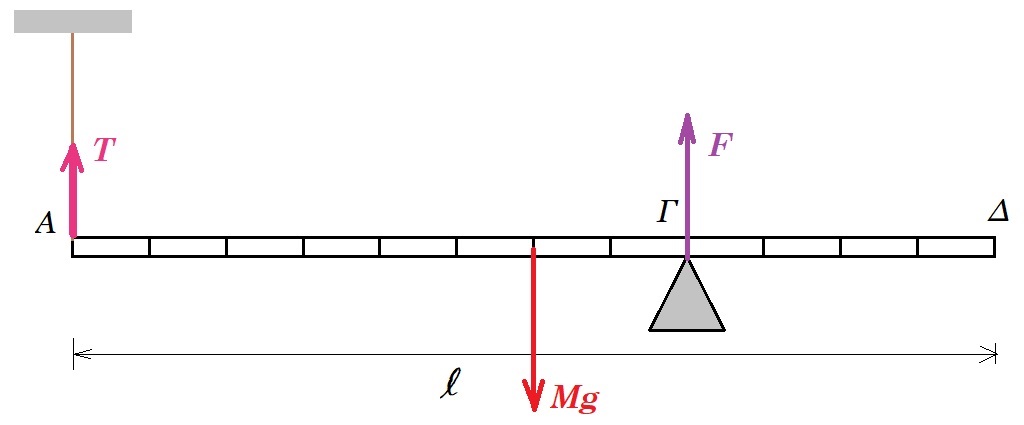
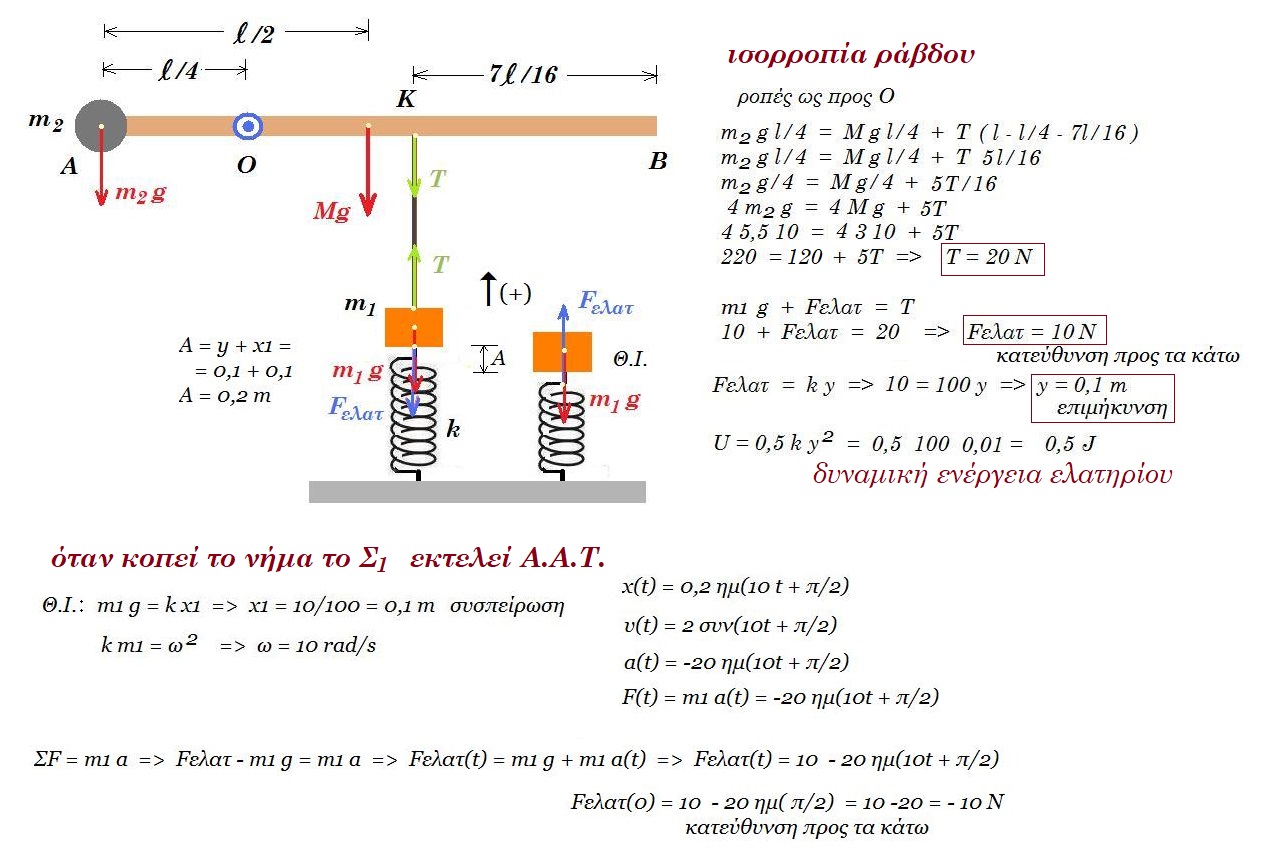
 Στο σχήμα (α) φαίνεται μια ομογενής, λεπτή και ισοπαχής ράβδος μήκους ℓ = 1,2 m, μάζας Μ και βάρους 30 Ν. Το άκρο Α της ράβδου είναι δεμένο σε αβαρές κατακόρυφο νήμα, το άλλο άκρο του οποίου είναι ακλόνητα στερεωμένο. Η ράβδος βρίσκεται σε επαφή με στήριγμα στο σημείο Γ, το οποίο απέχει από το άκρο Α απόσταση 𝛢𝛤 = 2ℓ/3. Η ράβδος ισορροπεί σε οριζόντια θέση. Η ροπή αδράνειας της ράβδου ως προς κατακόρυφο άξονα, ο οποίος περνά από το σημείο Γ και είναι κάθετος στη ράβδο δίνεται από τη σχέση 𝐼 = 1/9 𝑀ℓ2.
Στο σχήμα (α) φαίνεται μια ομογενής, λεπτή και ισοπαχής ράβδος μήκους ℓ = 1,2 m, μάζας Μ και βάρους 30 Ν. Το άκρο Α της ράβδου είναι δεμένο σε αβαρές κατακόρυφο νήμα, το άλλο άκρο του οποίου είναι ακλόνητα στερεωμένο. Η ράβδος βρίσκεται σε επαφή με στήριγμα στο σημείο Γ, το οποίο απέχει από το άκρο Α απόσταση 𝛢𝛤 = 2ℓ/3. Η ράβδος ισορροπεί σε οριζόντια θέση. Η ροπή αδράνειας της ράβδου ως προς κατακόρυφο άξονα, ο οποίος περνά από το σημείο Γ και είναι κάθετος στη ράβδο δίνεται από τη σχέση 𝐼 = 1/9 𝑀ℓ2.
(α) Να μεταφέρετε το σχήμα στο τετράδιο απαντήσεων και να σχεδιάσετε όλες τις δυνάμεις που ασκούνται στη ράβδο.
(β) Να υπολογίσετε το μέτρο της τάσης που ασκεί το νήμα στη ράβδο.
(γ) Να προσδιορίσετε το μέτρο και την κατεύθυνση της δύναμης που δέχεται το στήριγμα από τη ράβδο.
(δ) Κόβουμε από τη ράβδο τμήμα μήκους ℓ/6 και το τοποθετούμε πάνω στη ράβδο, όπως φαίνεται στο σχήμα (β). Να αναφέρετε αν θα αλλάξει η δύναμη που δέχεται το στήριγμα από τη ράβδο, που υπολογίσατε στο ερώτημα (β).
σχήμα (β) 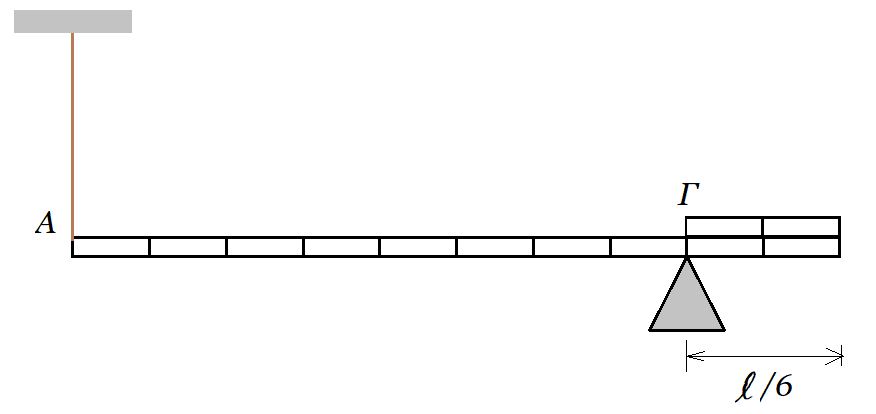
ισορροπία ράβδου : ΣFy = 0 => T + F - Mg = 0
Στ(Α) = 0 => F 2l/3 - Mg l/2 = 0 => F 2/3 = 30 1/2 = 0 => F = 22,5 N
Στ(Γ) = 0 => Mg l/6 - Τ 2l/3 = 0 => Τ 2/3 = 30 1/6 = 0 => Τ = 7,5 N
το στήριγμα στο σημείο Γ δέχεται από την ράβδο δύναμη αντίθετη της F
ισορροπία ράβδου : ΣFy = 0 => T' + F' - (m1 + m2) g = 0 m1 = 8/12 M = 2M/3 m2 = M/3
Στ(Α) = 0 => F' 2l/3 - m1 g 4l/12 - m1 g 9l/12 = 0 => F' 8/12 = 20 4/12 + 10 9/12 = 0 => F' = 170/8 N
Στ(Γ) = 0 => - Τ' 2l/3 + m1 g 4l/12 - m1 g l/12 = 0 => Τ' 8/12 = 20 4/12 - 10 1/12 = 0 => Τ' = 70/8 N

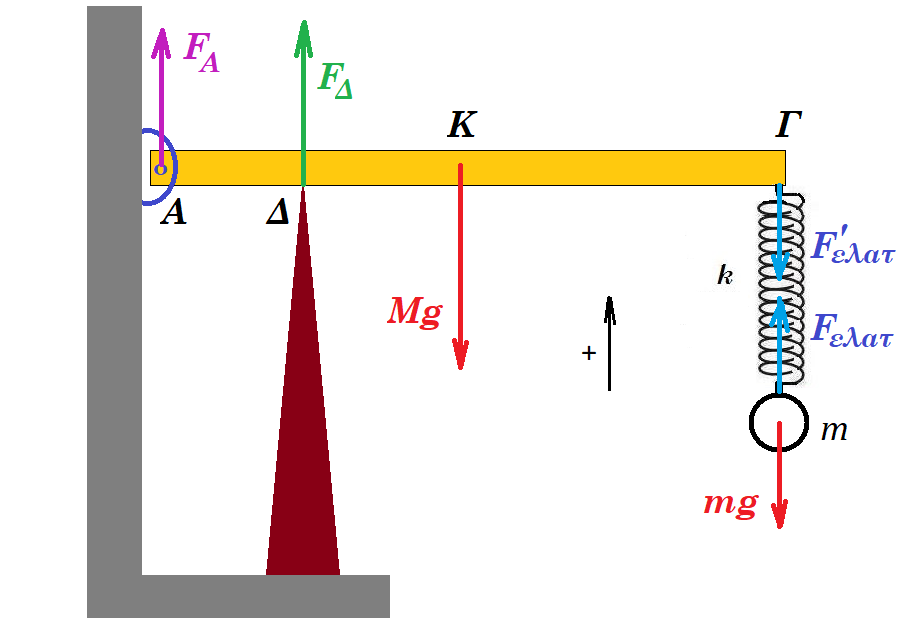
Στο σχήμα η ομογενής ράβδος ΑΓ έχει μήκος ΑΓ = ℓ μάζα Μ = 4 Kg και συνδέεται με άρθρωση σε τοίχο με το άκρο της Α. Στο σημείο Δ, με ΑΔ = ℓ/4 υπάρχει υποστήριγμα και στο άκρο Γ είναι στερεωμένο το πάνω άκρο ιδανικού ελατηρίου σταθεράς k = 100 Ν/m, στο κάτω άκρο του οποίου έχει συνδεθεί σφαιρίδιο (Σ) μάζας m = 1 Kg. Η ράβδος και το σφαιρίδιο ισορροπούν και η ράβδος είναι οριζόντια.
Α. Υπολογίστε τα μέτρα των δυνάμεων που ενεργούν στη ράβδο.
Β. Εκτρέπουμε το σφαιρίδιο κατακόρυφα προς τα πάνω κατά d = 0,2 m και στη συνέχεια το αφήνουμε ελεύθερο τη χρονική στιγμή t0 = 0 οπότε αρχίζει να εκτελεί απλή αρμονική ταλάντωση.
Β1. Υπολογίστε την ενέργεια της ταλάντωσης
Β2. Γράψτε την εξίσωση απομάκρυνσης – χρόνου x(t)
Β3. Γράψτε την εξίσωση της δύναμης που ασκεί το ελατήριο στο σφαιρίδιο (Σ), σε συνάρτηση με το χρόνο.
Β4. Γράψτε την εξίσωση της δύναμης που ασκείται στη ράβδο στο σημείο της άρθρωσης, Α , σε συνάρτηση με την απομάκρυνση της α.α.τ. και παραστήστε την γραφικά.
Γ. Ποιο το μέγιστο πλάτος των ταλαντώσεων του συστήματος ελατήριο – σφαιρίδιο (Σ) με τη ράβδο να παραμένει ακίνητη;
Δίνεται g = 10m/s2
(Α) ισορροπία σφαίρας : mg = Fελατ => 10 Ν = 100 Ν/m x0 => x0 = 0,1 m επιμήκυνση ελατηρίου κατά την ισορροπία της σφαίρας
η ράβδος δέχεται στο άκρο της Γ από το ελατήριο δύναμη F'ελατ = - Fελατ = - 10 Ν
ισορροπία ράβδου ΑΓ : ροπές ως προς Α : - Mg l/2 + F'ελατ l + FΔ l/4 = 0 =>
=> - 40 l/2 - 10 l + FΔ l/4 = 0 => FΔ = 120 Ν κατακόρυφη προς τα επάνω
ροπές ως προς Δ : - Mg l/4 + F'ελατ 3l/4 + FΑ (- l/4) = 0 =>
=> - 40 l/4 - 10 3l/4 - FΑ l/4 = 0 =>
=> - 40 - 30 - FΑ => FΑ = - 70 Ν κατακόρυφη προς τα κάτω
επαλήθευση : ΣF = 0 => FΔ + Mg + F'ελατ + FΑ = 0 => + 120 - 70 - 40 - 10 = 0
(Β) στην ισορροπία η επιμήκυνση του ελατηρίου είναι x0 = 0,1 m
ω2 = k / m = 100 / 1 => ω = 10 rad/s f = ω / 2π = 5/π Hz T = 1/f = π/5 s
E = ½ k d2 = ½ 100 0,22 = 2 Joule ενέργεια της ταλάντωσης της σφαίρας
x(t) = 0,2 ημ(10t +π/2) x(0) = + 0,2 m
v(t) = 2 συν(10t +π/2) α(t) = - 20 ημ(10t +π/2)
ΣF = mα => mg + Fελατ = mα => - 10 + Fελατ = - 20 ημ(10t +π/2) =>
=> Fελατ(t) = 10 - 20 ημ(10t +π/2)
άρα F'ελατ(t) = - 10 + 20 ημ(10t +π/2) ή
F'ελατ(x) = - 10 + 20 5 x = - 10 + 100x - 0,2 m £ x £ + 0,2 m
ροπές ως προς Δ : - Mg l/4 + F'ελατ 3l/4 + FΑ (- l/4) = 0 =>
=> - 40 l/4 + (- 10 + 20 ημ(10t +π/2) ) 3l/4 - FΑ l/4 = 0 =>
=> - 40 - 30 + 60 ημ(10t +π/2) - FΑ =>
=> FΑ(t) = - 70 + 60 ημ(10t +π/2) κατακόρυφη
FΑ(t) = - 70 + 300 x - 0,2 m £ x £ + 0,2 m
ροπές ως προς Α : - Mg l/2 + F'ελατ l + FΔ l/4 = 0 =>
=> - 40 l/2 + {- 10 + 20 ημ(10t +π/2)} l + FΔ l/4 = 0 =>
=> - 80 + 4 (- 10 + 20 ημ(10t +π/2) ) + FΔ = 0 =>
=> FΔ(t) = 120 - 80 ημ(10t +π/2) κατακόρυφη
FΔ = 120 - 400 x - 0,2 m £ x £ + 0,2 m
δυναμική ενέργεια της σφαίρας κατά την ταλάντωση :
U = ½ k x2 = ½ 100 [ 0,2 ημ(10t + π/2) ]2 => U = 2 ημ2(10t + π/2)
κινητική ενέργεια της σφαίρας κατά την ταλάντωση :
Κ = ½ m v2 = ½ 1 [ 2 συν(10t + π/2) ]2 => Κ = 2 συν2(10t + π/2)
ρυθμός μεταβολής της δυναμικής ενέργειας της σφαίρας κατά την ταλάντωση :
dU/dt = k x dx/dt = k x v = 100 0,2 ημ(10t +π/2) 2 συν(10t +π/2) =
= 4 ημ(10t + π/2) συν(10t + π/2) =>
=> dU(t)/dt = 20 ημ(20t + π) = - 20 συν20t
ρυθμός μεταβολής της κινητικής ενέργειας της σφαίρας κατά την ταλάντωση :
dΚ/dt = m v dv/dt = m v a = 1 2 συν(10t +π/2) [ -20 ημ(10t +π/2) ] =
= - 40 συν(10t + π/2) ημ(10t + π/2) =>
=> dΚ(t)/dt = - 20 ημ(20t + π) = 20 συν20t
δυναμική ενέργεια του ελατηρίου κατά την ταλάντωση :
Uελατ = ½ k (x + x0)2 = ½ 100 (x - 0,1)2 => Uελατ(x) = 50 (x - 0,1)2 - 0,2m £ x £ + 0,2m
Uελατ(- 0,2m) = 50 (- 0,2 - 0,1)2 = 4,5 J Uελατ(- 0,1m) = 50 (- 0,1 - 0,1)2 = 2 J Uελατ(0) = 50 (- 0,1)2 = 0,5 J
Uελατ(+ 0,1m) = 50 (+ 0,1 - 0,1)2 = 0 J Uελατ(+ 0,2m) = 50 (+ 0,2 - 0,1)2 = 0,5 J
Uελατ = ½ k (x + x0)2 = ½ 100 [ 0,2 ημ(10t + π/2) - 0,1 ]2 => Uελατ(t) = 50 [ 0,2 ημ(10t + π/2) - 0,1 ]2
Uελατ(0) = 50 [ 0,2 ημ(π/2) - 0,1 ]2 = 50 ( 0,2 - 0,1 )2 = 0,5 J = Uελατ(+ 0,2m) άνω άκρο ταλάντωσης σφαίρας
Uελατ(π/20) = 50 [ 0,2 ημ(10 π/20 + π/2) - 0,1 ]2 = 50 [ 0,2 ημ(π) - 0,1 ]2 =
= 50 ( - 0,1 )2 = 0,5 J = Uελατ(0m) θέση ισορροπίας σφαίρας
Uελατ(π/10) = 50 [ 0,2 ημ(10 π/10 + π/2) - 0,1 ]2 = 50 [ 0,2 ημ(3π/2) - 0,1 ]2 =
= 50 (- 0,2 - 0,1)2 = 4,5 J = Uελατ(-0,2m) κάτω άκρο ταλάντωσης σφαίρας
Uελατ(3π/20) = 50 [ 0,2 ημ(10 3π/20 + π/2) - 0,1 ]2 = 50 [ 0,2 ημ(2π) - 0,1 ]2 =
= 50 (- 0,1)2 = 0,5 J = Uελατ(0m) θέση ισορροπίας σφαίρας
Uελατ(π/5) = 50 [ 0,2 ημ(10 π/5 + π/2) - 0,1 ]2 = 50 [ 0,2 ημ(π/2) - 0,1 ]2 =
= 50 ( 0,2 - 0,1 )2 = 0,5 J = Uελατ(+0,2m) άνω άκρο ταλάντωσης σφαίρας
(Γ) FΔ = 0 => 120 - 400 x = 0 => x = 120 / 400 = 0,3 m μέγιστο πλάτος ταλάντωσης της
η ράβδος χάνει την επαφή της με το στήριγμα στο σημείο Δ όταν FΔ = 0
ροπές ως προς Α : - Mg l/2 + F'ελατ l + FΔ l/4 = 0 => - 40 l/2 + (-10 + 100x) l = 0 =>
=> - 40 - 20 + 200x = 0 => x = 0,3 m
όταν x = + 0,3 m η σφαίρα είναι στην ανώτερη θέση ταλάντωσης και το ελατήριο είναι συσπειρωμένο κατά 0,2 m
x(t) = A ημ(10t +π/2) v(t) = 10A συν(10t +π/2) α(t) = - 100A ημ(10t +π/2)
Fελατ(t) = 10 - 100A ημ(10t +π/2) F'ελατ(t) = - 10 + 100A ημ(10t +π/2)
FΔ(t) = 120 - 400A ημ(10t +π/2) => FΔ = 120 - 400x FΔ = 0 => x = 0,3 m
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
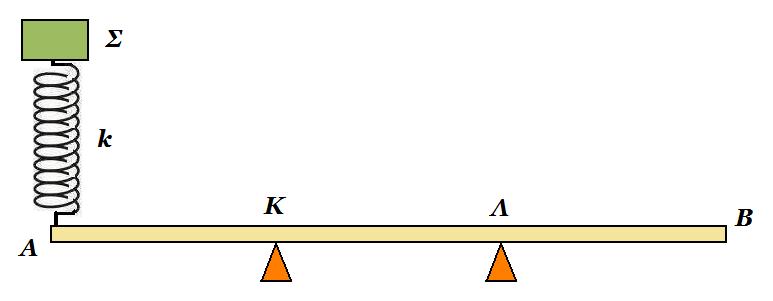 Η ομογενής δοκός ΑΒ του σχήματος, μήκους ℓ=3m και μάζας Μ=20kg ισορροπεί σε οριζόντια θέση, στηριζόμενη σε δύο στηρίγματα στα σημεία Κ και Λ, όπου (ΑΚ)=(ΚΛ)= (ΛΒ)=1m. Στο άκρο Α έχει στερεωθεί ιδανικό ελατήριο σταθεράς k=100Ν/m, στο πάνω άκρο του οποίου ισορροπεί σώμα Σ, μάζας m=4kg.
Η ομογενής δοκός ΑΒ του σχήματος, μήκους ℓ=3m και μάζας Μ=20kg ισορροπεί σε οριζόντια θέση, στηριζόμενη σε δύο στηρίγματα στα σημεία Κ και Λ, όπου (ΑΚ)=(ΚΛ)= (ΛΒ)=1m. Στο άκρο Α έχει στερεωθεί ιδανικό ελατήριο σταθεράς k=100Ν/m, στο πάνω άκρο του οποίου ισορροπεί σώμα Σ, μάζας m=4kg.
- Να υπολογιστούν οι δυνάμεις που δέχεται η δοκός από τα δύο στηρίγματα.
- Μετακινούμε το σώμα Σ κατακόρυφα προς τα κάτω κατά d=0,5m και τη στιγμή t=0, το αφήνουμε να ταλαντωθεί.
α) Να γράψετε την εξίσωση της απομάκρυνσης του Σ από τη θέση ισορροπίας του σε συνάρτηση με το χρόνο, θεωρώντας την προς τα κάτω κατεύθυνση θετική.
β) Εκφράστε την δύναμη αντίδρασης Ν2 στο σημείο Λ συναρτήσει του χρόνου. Ποιά είναι η μέγιστη και η ελάχιστη τιμή της αντίδρασης Ν2, που δέχεται η δοκός από το στήριγμα στο σημείο Λ;
γ) Ποιο το μέγιστο δυνατό πλάτος ταλάντωσης του σώματος Σ, χωρίς η δοκός να χάνει την επαφή με κάποιο από τα στηρίγματα; Δίνεται g=10m/s2.
θετική κατεύθυνση : κατακόρυφη προς τα κάτω
ισορροπία Σ : mg + F'ελατ = 0 => F'ελατ = - 40 Ν και στο άλλο άκρο του ελατηρίου : Fελατ = - F'ελατ = + 40 Ν
F'ελατ = k Δl => Δl = 40 / 100 = 0,4 m αρχική συσπείρωση ελατηρίου
ισορροπία δοκού : Μg + Fελατ + Ν1 + Ν2 = 0 => Ν1 + Ν2 = - 200 - 40 => Ν1 + Ν2 = - 240 Ν
ροπές ως προς Κ : Στ(Κ) = 0 => Fελατ (ΑΚ) + Ν2 (ΚΛ) + Μg ( ℓ/2 - ΑΚ ) = 0 =>
=> 40 1 + Ν2 1 + 200 0,5 = 0 => Ν2 = - 60 Ν
ροπές ως προς Λ : Στ(Λ) = 0 => Fελατ (ΑΛ) + Ν1 (ΚΛ) + Μg ( ℓ/2 - ΒΛ ) = 0 =>
=> 40 2 + Ν1 1 + 200 0,5 = 0 => Ν1 = - 180 Ν
ω2 = k / m = 100 / 4 = 25 => ω = 5 rad/s T = 2π/ω = 2π/5 s
x(t) = 0,5 ημ(5t + π/2) v(t) = 2,5 συν(5t + π/2) α(t) = - 12,5 ημ(5t + π/2)
ΣF = ma => F'ελατ + mg = ma => F'ελατ (t) = - 40 - 50 ημ(5t + π/2) και Fελατ (t) = 40 + 50 ημ(5t + π/2)
ροπές ως προς Λ : Στ(Λ) = 0 => Fελατ (ΑΛ) + Ν1 (ΚΛ) + Μg ( ℓ/2 - ΒΛ ) = 0 =>
=> ( 40 + 50 ημ(5t + π/2) ) 2 + Ν1 1 + 200 0,5 = 0 => Ν1(t) = - 180 - 100 ημ(5t + π/2)
Μg + Fελατ + Ν1 + Ν2 = 0 => 200 + 40 + 50 ημ(5t + π/2) + Ν2 + ( - 180 - 100 ημ(5t + π/2) ) = 0 => 60 + Ν2 - 50 ημ(5t + π/2) = 0 => Ν2(t) = - 60 + 50 ημ(5t + π/2)
t = 0 Ν2(0) = - 60 + 50 ημ(π/2) = - 60 + 50 = - 10 N ελάχιστη δύναμη κατακόρυφη προς τα πάνω
Ν1(0) = - 180 - 100 ημ(π/2) = - 280 Ν
Fελατ = 40 + 50 ημ(π/2) = 40 + 50 = 90 Ν και
F'ελατ = - 90 N το ελατήριο συσπειρώνεται κατά 90 Ν / 100 N/m = 0,9 m
t = T/4 = π/10 s Ν2 = - 60 + 50 ημ(5 π/10 + π/2 ) = - 60 + 50 ημ(π) = - 60 Ν
Ν1 = - 180 - 100 ημ(5 π/10 + π/2) = - 180 Ν
Fελατ = 40 + 50 ημ(5 π/10 + π/2) = 40 + 50 ημπ = 40 Ν = mg και
F'ελατ = - 40 N το ελατήριο συσπειρώνεται κατά 40 Ν / 100 N/m = 0,4 m
t = T/2 = π/5 s Ν2 = - 60 + 50 ημ(5 π/5 + π/2 ) = - 60 + 50 ημ(3π/2) = - 110 N μέγιστη δύναμη κατακόρυφη προς τα πάνω
Ν1 = - 180 - 100 ημ(5 π/5 + π/2) = - 180 + 100 = - 80 Ν
Fελατ = 40 + 50 ημ(5 π/5 + π/2) = 40 + 50 ημ(3π/2) = 40 - 50 = - 10 Ν και
F'ελατ = + 10 N το ελατήριο επιμηκύνεται κατά 10 Ν / 100 N/m = 0,1 m
t = 3T/4 = 3π/10 s Ν2 = - 60 + 50 ημ(5 3π/10 + π/2 ) = - 60 - 50 ημ(2π) = - 60 Ν
Ν1 = - 180 - 100 ημ(5 3π/10 + π/2) = - 180 Ν
Fελατ = 40 + 50 ημ(5 3π/10 + π/2) = 40 + 50 ημ2π = 40 Ν = mg και
F'ελατ = - 40 N το ελατήριο συσπειρώνεται κατά 40 Ν / 100 N/m = 0,4 m
έστω Α το πλάτος της ταλάντωσης του σώματος Σ τότε : x = Α ημ(5t + π/2)
ΣF = - D x => F'ελατ + mg = - k x => F'ελατ + 40 = - 100 Α ημ(5t + π/2) => F'ελατ = - 40 - 100 Α ημ(5t + π/2)
τότε Fελατ = + 40 + 100 Α ημ(5t + π/2)
Ν2(t) = - 60 + 100 Α ημ(5t + π/2)
η δύναμη Ν2 γίνεται ελάχιστη την στιγμή t = T = 2π/5 s
τότε Ν2(2π/5) = - 60 + 100 Α ημ(5 2π/5 + π/2) = - 60 + 100 Α ημ(π/2) = - 60 + 100 Α
Ν2 = 0 => - 60 + 100 Α = 0 => Α = 0,6 m όταν το πλάτος της ταλάντωσης του σώματος Σ είναι μεγαλύτερο ή ίσο από 0,6 m η δοκός χάνει την επαφή της με το στήριγμα Λ
Ν1(t) = - 180 - 100 ημ(5t + π/2)
η δύναμη Ν1 γίνεται ελάχιστη την στιγμή t = T/2 = π/5 s
τότε Ν1(π/5) = - 180 - 100 Α ημ(5 π/5 + π/2) = - 180 - 100 Α ημ(3π/2) = - 180 + 100 Α
Ν1 = 0 => - 180 + 100 Α = 0 => Α = 1,8 m όταν το πλάτος της ταλάντωσης του σώματος Σ είναι μεγαλύτερο ή ίσο από 1,8 m η δοκός χάνει την επαφή της με το στήριγμα Κ
x(t) = 1,8 ημ(5t + π/2) v(t) = 9 συν(5t + π/2) α(t) = - 45 ημ(5t + π/2)
ΣF = ma => F'ελατ + mg = ma => F'ελατ (t) = - 40 - 180 ημ(5t + π/2) και Fελατ (t) = 40 + 180 ημ(5t + π/2) το ελατήριο έχει επιμήκυνση 140 N / 100 N/m= 1,4 m
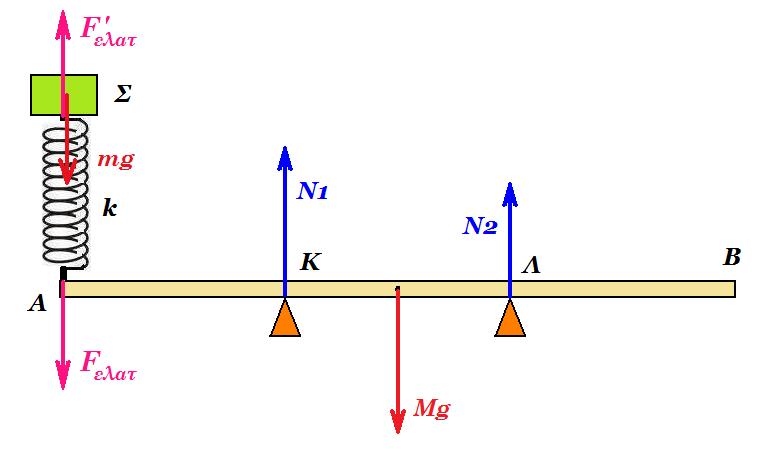
1. Μια ομογενής ράβδος μήκους ℓ = 2 m και μάζας Μ = 5 kg ισορροπεί σε οριζόντια θέση στηριγμένη σε δύο στηρίγματα που απέχουν d = 0,5 m από κάθε άκρο της ράβδου. Στο ένα άκρο της ράβδου κρέμεται μέσω ελατηρίου σταθεράς k = 80 N/m σώμα Σ μάζας m = 3,2 kg.
α) Να βρείτε τη δύναμη που ασκεί κάθε στήριγμα στη ράβδο όταν το σώμα Σ ισορροπεί.
β ) Απομακρύνουμε το σώμα Σ προς τα κάτω κατά Α και το αφήνουμε ελεύθερο να κινηθεί τη χρονική στιγμή t = 0. Να βρείτε τη μέγιστη τιμή του Α για να μην ανατραπεί η ράβδος.
γ) Για την τιμή του Α που βρήκατε στο (β) ερώτημα:
(i) Να βρείτε τις εξισώσεις της απομάκρυνσης σαν συνάρτηση του χρόνου για το σώμα Σ, καθώς και της δύναμης του ελατηρίου που ασκείται στη ράβδο σαν συνάρτηση του χρόνου.
(ii) Να βρείτε τις εξισώσεις της αντίδρασης κάθε στηρίγματος σαν συνάρτηση του χρόνου και να τις παραστήσετε γραφικά σε βαθμολογημένους άξονες.
Να θεωρήσετε θετική φορά προς τα κάτω και g =10 m/s2 .
[ α) 73 N, 9 N β) 0,225 m γ) (i) x=0,225ημ(5t+π/2), F =32+18ημ(5t+π/2) ΕΛ (ii) F =73+27ημ(5t+π/2), F =9-9ημ(5t+π/2) ] 
(Α) ισορροπία Σ : m g = k x0 => 32 = 80 x0 => x0 = 0,4 m
ροπές ως προς Β : M . g . (L/2 - d) + k x0 . (L - d) = FΓ . (L - 2d) => 5 . 10 . (1 - 0,5) + 32 . (2 - 0,5) = FΓ . (2 - 1) => 25 + 48 = FΓ => FΓ = 73 Ν κατακόρυφη προς τα πάνω
ροπές ως προς Γ : M . g . (L/2 - d) = k x0 . d + FΒ . (L - 2d) => 5 . 10 . (1 - 0,5) = 32 . 0,5 + FΓ . (2 - 1) => 25 = 16 = FΒ => FΒ = 9 Ν κατακόρυφη προς τα πάνω
(Β) ανατροπή ράβδου θα συμβεί όταν FΒ = 0 τότε το ελατήριο είναι επιμηκυμένο κατά x1
ροπές ως προς Γ : M . g . (L/2 - d) = k x1 . d + FΒ . (L - 2d) => M . g . (L/2 - d) = k x1 . d => 50 . 0,5 = 80 . x1 . 0,5 => x1 = 0,625 m συνεπώς απομακρύναμε το σώμα Σ προς τα κάτω κατά Α = x1 - x0 = 0,625 - 0,4 = 0,225 m
το σώμα Σ ταλαντώνεται με πλάτος Α = 0,225 m και κυκλική συχνότητα ω : k = m ω2 => 80 = 3,2 ω2 => ω2 = 25 => ω = 5 rad/s
x(t) = 0,225 συν5t = 0,225 ημ(5t + π/2) υ(t) = 1,125 συν(5t + π/2)
α(t) = - 5,625 ημ(5t + π/2) F(t) = m a(t) = 3,2 . [ - 5,625 ημ(5t + π/2) ] = - 18 ημ(5t + π/2)
για τη δύναμη ελατηρίου μετράμε από το φυσικό μήκος του ελατηρίου : Fελατ(t) = k . [ x0 + x(t) ] = 80 . [ 0,4 + 0,225 ημ(5t + π/2) ] = 32 + 18 ημ(5t + π/2)
(Γ) ροπές ως προς Β : M.g . (L/2 - d) + Fελατ . (L - d) = FΓ . (L - 2d) => 50 . 0,5 + { 32 + 18 ημ(5t + π/2) }. 1,5 = FΓ . 1 => FΓ (t) = 73 + 27 ημ(5t + π/2)
ροπές ως προς Γ : M . g . (L/2 - d) = Fελατ . d + FΒ . (L - 2d) => 50. 0,5 = { 32 + 18 ημ(5t + π/2) }. 0,5 + FΒ . 1 => FΒ (t) = 9 - 9 ημ(5t + π/2)
2. Λεία οριζόντια σανίδα μήκους L = 3 m και μάζας Μ = 0,4 Kg αρθρώνεται στο άκρο της Α σε κατακόρυφο τοίχο. Σε απόσταση d = 1 m από τον τοίχο, η σανίδα στηρίζεται ώστε να διατηρείται οριζόντια. Ιδανικό αβαρές ελατήριο σταθεράς k = 100 Ν/m συνδέεται με το ένα άκρο του στον τοίχο και το άλλο σε σώμα Σ1 μάζας m1 = 1 Kg. Το ελατήριο βρίσκεται στο φυσικό του μήκος, ο άξονάς του είναι οριζόντιος και διέρχεται από το κέντρο μάζας του σώματος Σ1. Το κέντρο μάζας του σώματος Σ1 βρίσκεται σε απόσταση d από τον τοίχο.
Στη συνέχεια, ασκούμε στο σώμα Σ1 σταθερή οριζόντια δύναμη μέτρου F = 40 N με κατεύθυνση προς το άλλο άκρο Γ της σανίδας. Όταν το σώμα Σ1 διανύσει απόσταση s = 5 cm, η δύναμη παύει να ασκείται στο σώμα και, στη συνέχεια, το σώμα εκτελεί απλή αρμονική ταλάντωση.
Δ1) Να υπολογίσετε το πλάτος της απλής αρμονικής ταλάντωσης που θα εκτελέσει το σώμα Σ1.
Δ2) Να εκφράσετε το μέτρο της δύναμης FA που δέχεται η σανίδα από τον τοίχο σε συνάρτηση με την απομάκρυνση του σώματος Σ1 και να σχεδιάσετε την
αντίστοιχη γραφική παράσταση.
Κατά μήκος της σανίδας από το άκρο Γ κινείται σώμα Σ2 μάζας m2 = 1 Kg με ταχύτητα υ2 = 2√3 m/s. Τα δύο σώματα συγκρούονται κεντρικά και ελαστικά, όταν
η απομάκρυνση του σώματος Σ1 είναι x1 , όπου x1 ≥ 0. Το σώμα Σ1 μετά την κρούση ταλαντώνεται με πλάτος διπλάσιο απ'ότι προηγουμένως.
Δ3) Να βρείτε την απομάκρυνση x1 .
Δ4) Να βρείτε μετά από πόσο χρονικό διάστημα από τη στιγμή της κρούσης τα δύο σώματα θα συγκρουστούν για δεύτερη φορά.
Θεωρούμε θετική τη φορά της απομάκρυνσης προς το Γ και g = 10m/s2 . [ α) 0,2 m β) FA = -2-10x (SI) γ) 0,2 m δ) 2π/15 s ] 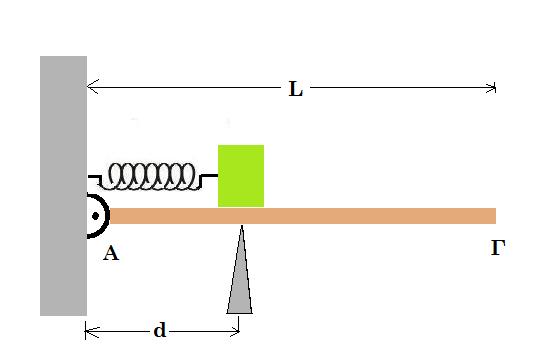
(Δ1) η δύναμη παράγει έργο συνεπώς το σώμα έχει αποκτήσει κινητική ενέργεια και το ελατήριο δυναμική ενέργεια WF = K + U = Kmax = Umax =>
=> F . s = 40 N . 0,05 m = 2 J = 0,5 . k . A2 = 0,5 . 100 Ν/m . A2 => A2 = 0,04 => A = 0,2 m το σώμα θα εκτελέσει ταλάντωση με πλάτος A = 0,2 m
(Δ2) έστω x προς το άκρο Γ είναι η απομάκρυνση του σώματος από τη θέση ισορροπίας, η σανίδα μένει σε οριζόντια θέση παίρνουμε ροπές ως προς το στήριγμα :
Μ . g . (L/2 - d) + m . g . x + FA . d = 0 => 0,4 . 10 . (3/2 - 1) + 1 .10 . x + FA . 1 = 0 =>
=> 2 + 10 . x + FA = 0 => FA = - 2 - 10x (S.I.)
(Δ3) το Σ1 απέχει x1 από τη Θ.Ι. έχει ταχύτητα υ1 : ½ . k . A2 = ½ . k . x12 + ½ . m . υ12 =>
=> ½ . 100 . 0,22 = ½ . 100 . x12 + ½ . 1 . υ12 => 4 = 100 . x12 + υ12 (1)
κεντρική - ελαστική κρούση : υ1' = (m1 - m2 ) / (m1 + m2 ) . υ1 + 2 . m2 . υ2 / (m1 + m2 ) =
= 2 . 1 . (- 2√3) / 2 = - 2√3 m/s επειδή τα σώματα έχουν ίσες μάζες κατά την κρούση ανταλλάσουν ταχύτητες, τότε το Σ1 ταλαντώνεται με πλάτος διπλάσιο απ'ότι προηγουμένως : Α' = 0,4 m = 2 Α
½ . k . (A')2 = ½ . k . x12 + ½ . m . (υ1')2 => ½ . 100 . 0,42 = ½ . 100 . x12 + ½ . 1 . (2√3 )2 => 8 = 50 . x12 + 6 => x12 = 2/50 = 4/100 => x1 = Φ0,04 = 0,2 m
από τη σχέση (1) έχουμε : 4 = 100 . x12 + υ12 => 4 = 100 . 0,22 + υ12 => 4 = 4 + υ12 => υ1 = 0 δηλαδή όταν συγκρούονται τα σώματα το Σ1 βρίσκεται στην ακραία θέση ταλάντωσης και στιγμιαία είναι ακίνητο, συνεπώς μετά την κρούση το Σ2 ακινητοποιείται υ2' = 0
(Δ4) ω2 = k / m = 100 / 1 => ω = 10 rad/s = 2π / Τ => Τ = π/5 s
έστω ότι η κρούση γίνεται δεξιά από τη Θ.Ι. προς το σημείο Γ το Σ1 : x1 = A' ημωt1 => => 0,2 = 0,4 ημ10t1 => ημ10t1 = 0,5 = ημ(π - π/6) ( η ταχύτητα είναι αρνητική ) =>
=> 10t1 = 2Νπ + 5π/6 => t1 = Νπ/5 + 5π/60 s Ν = 0, 1, 2, ... για Ν = 0 t1 = 5π/60 s ο χρόνος από το σημείο σύγκρουσης μέχρι τη Θ.Ι. είναι Τ/2 - 5π/60 = π/10 - 5π/60 = π/60 s
το Σ1 κινείται με υ1' = - 2√3 m/s ( δηλαδή προς το άκρο Α ) ενώ το Σ2 ακινητοποιείται, θα συγκρουστούν πάλι μετά από χρόνο : π/60 + Τ/2 + π/60 = π/10 + π/30 = 4π/30 = 2π/15 s
έστω ότι η κρούση γίνεται αριστερά από τη Θ.Ι. προς το σημείο Α το Σ1 : x1 = A' ημωt1 => - 0,2 = 0,4 ημ10t1 => ημ10t1 = - 0,5 = ημ(π + π/6) ( η ταχύτητα είναι αρνητική ) =>
=> 10t1 = 2Νπ + 7π/6 => t1 = Νπ/5 + 7π/60 s Ν = 0, 1, 2, ... για Ν = 0 t1 = 7π/60 s
το Σ1 κινείται με υ1' = - 2√3 m/s ( δηλαδή προς το άκρο Α ) ενώ το Σ2 ακινητοποιείται, θα συγκρουστούν πάλι μετά από χρόνο : ( 3Τ/4 - 7π/60 ) + ( 3Τ/4 - 7π/60 ) = = 3Τ/2 - 7π/30 s = 3π/10 - 7π/30 = 2π/30 = π/15 s
x(m) - 0,4 - 0,2 0 0,2 0,4 ο χρόνος για να πάει το σώμα από τη Θ.Ι. στη θέση +Α/2 είναι π/60 sec
t(s) 0 π/60 π/20 από τη Θ.Ι. στην ακραία θέση +Α είναι Τ/4 = π/20 sec
π/20 - π/60 = π/30 από την ακραία θέση +Α στη θέση +Α/2 είναι Τ/4 - π/60 = π/20 - π/60 = 2π/60 = π/30 sec
από την ακραία θέση +Α στη θέση -Α/2 είναι Τ/4 + π/60 = π/20 + π/60 = 4π/60 = π/15 s
υ = (0,4 + 0,2) / π/15 = 2,864 m/s < 2√3 m/s = 3,464 m/s
3.
4. Ομογενής άκαμπτη ράβδος ΑΖ άχει μήκος L = 4 m, μάζα M = 3 kg, ισορροπεί σε οριζόντια θέση. Στο άκρο Α υπάρχει ακλόνητη άρθρωση γύρω από την οποία η ράβδος μπορεί να περιστρέφεται, χωρίς τριβές ενώ στο άλλο άκρο Ζ υπάρχει στερεωμένο σφαιρίδιο μάζας m1 = 0,6 kg και αμελητέων διαστάσεων. Ένα αβαρές τεντωμένο νήμα ΔΓ συνδέει το σημείο Γ της ράβδου με σφαιρίδιο μάζας m2 = 1 kg, το οποίο είναι στερεωμένο στο ελεύθερο άκρο ιδανικού ελατηρίου σταθεράς k = 100 N/m. Το άλλο άκρο του ελατηρίου είναι ακλόνητο. Η απόσταση ΑΓ είναι ίση με 2,8 m. Όλη η διάταξη βρίσκεται στο ίδιο κατακόρυφο επίπεδο, στο οποίο γίνονται όλες οι κινήσεις.
(Α) Να υπολογίσετε :
Α1. τη ροπή αδράνειας του συστήματος ράβδου - σφαιριδίου m1 ως προς τον οριζόντιο άξονα που διέρχεται από το σημείο Α και είναι κάθετος στο επίπεδο της διάταξης, καθώς και του κέντρου μάζας του συστήματος ράβδου - σφαιριδίου m1
Α2. το μέτρο της τάσης του νήματος ΔΓ και την δύναμη που δέχεται η ράβδος στην άρθρωση Α
(Β) Αν κόψουμε το νήμα ΔΓ το σφαιρίδιο m2 εκτελεί αμείωτη αρμονική ταλάντωση, ενώ η ράβδος μαζί με το σώμα m1 υπό την επίδραση της βαρύτητας, περιστρέφονται χωρίς τριβές γύρω από το σημείο Α.
Να υπολογίσετε :
Β1. το χρόνο που χρειάζεται το σφαιρίδιο m2 από τη στιγμή που κόβεται το νήμα μέχρι τη στιγμή που θα φθάσει στην υψηλότερη θέση του για πρώτη φορά
Β2.πόση είναι η μικρότερη και η μεγαλύτερη τιμή της δυναμικής ενέργειας του ελατηρίου
Β3.το μέτρο της γραμμικής ταχύτητας του σημείου Ζ καθώς και του κέντρου μάζας του συστήματος ράβδου - σφαιριδίου m1, τη στιγμή που η ράβδος περνάει από την κατακόρυφη θέση
g = 10 m/s2 ροπή αδράνειας της ράβδου ως προς το κέντρο μάζας της Icm = 1/12 ML2 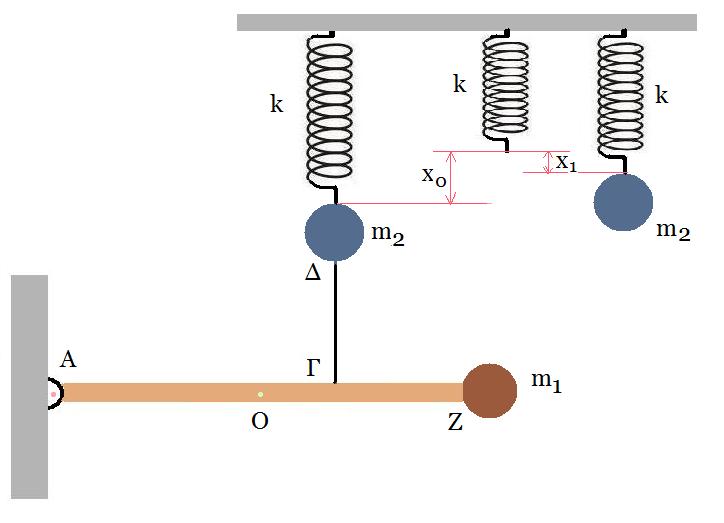
A1. I(A) = ICM + M (L/2)2 + m1 L2 = 1/12 M L2 + 1/4 M L2 + m1 L2 = 1/3 M L2 + m1 L2 = 1/3Χ3Χ16 + 0,6Χ16 = 1,6Χ16 = 25,6 kg m2
το κέντρο μάζας θα το βρούμε από τη σχέση : xcm = ( M . L/2 + m1 . L ) / ( M + m1 ) = ( 3 kg 2 m + 0,6 kg 4 m ) / ( 3 kg + 0,6 kg ) = 8,4/3.6 m = 7/3 m
A2. ροπές ως προς Α : Μ . g . L/2 + m1 . g . L - T . (ΑΓ) = 0 =>
=> 3 . 10 . 4/2 + 0,6 . 10 . 4 - T . 2,8 = 0 => Τ = 84/2,8 = 30 Ν
ΣFy = 0 => F(A) + T - M g - m1 g = 0 => F(A) = - T + M g + m1 g => F(A) = - 30 + 3 10 + 0,6 10 => F(A) = 6 N
Β1. ισορροπία m2 : m2 g + T - Fελατ = 0 => 1. 10 + 30 - k . x0 = 0 => x0 = 40/100 = 0,4 m αρχική επιμήκυνση ελατηρίου
το σύστημα ελατήριο - Σ2 ισορροπεί : m2 g = Fελατ => 1 .10 = k. x1 => x1 = 10/100 = 0,1 m επιμήκυνση
άρα το πλάτος ταλάντωσης θα είναι : Α = 0,4m - 0,1m = 0,3m
το σώμα m2 εκτελεί ΑΑΤ με κυκλική συχνότητα ω2 = k/m1 = 100/1 => ω = 10 rad/s
T = 2π/ω = 2π/10 = π/5 sec
στην ισορροπία το σώμα βρίσκεται στην κάτω άκραία θέση της ταλάντωσης θα πάει για πρώτη φορά στην άνω ακραία θέση σε χρόνο t = T/2 = π/10 sec
Β2. η εξίσωση της απομάκρυνσης συαρτήσει του χρόνου είναι: x(t) = A ημ(ωt + θ) => x(t) = 0,3 ημ(10t + π/2) = 0,3 συν10t ( θετική φορά προς τα κάτω )
ταχύτητα : υ(t) = 3 συν(10t + π/2) = - 3 ημ10t
επιτάχυνση : α(t) = - 30 ημ(10t + π/2) = - 30 συν10t = - k x(t)
δύναμη επαναφοράς : F(t) = m2 a(t) = - 30 συν10t
δύναμη ελατηρίου : ΣF = m2 a(t) => Fελατ + m2 g = m2 a(t) =>
=> Fελατ = - m2 g + m2 a(t) => Fελατ(t) = - 10 - 30 ημ(10t + π/2) = - k x1 - k x(t)
Fελατ(0) = - 10 - 30 ημ(π/2) = - 10 - 30 = - 40 Ν
στην ισορροπία του m2 το ελατήριο είναι επιμηκυμένο κατά 0,4 m οπότε η δύναμη ελατηρίου είναι Fελατ (0) = k . x0 = 100 N/m . 0,4 m = 40 N
δυναμική ενέργεια ταλάντωσης : U(t) = ½ k x(t)2 = ½ 100 0,32 ημ2(10t+π/2) = 4,5 ημ2(10t + π/2)
δυναμική ενέργεια ελατηρίου : Uελατ (t) = ½ k { x1 + x(t) }2 = ½ 100 { 0,1 + 0,3 ημ(10t+π/2) }2 => Uελατ (t) = 50 { 0,1 + 0,3 ημ(10t+π/2) }2
Uελατ (0) = 50 { 0,1 + 0,3 ημ(π/2) }2 = 50 0,42 = 8 J κάτω ακραία θέση της ταλάντωσης
Uελατ (Τ/2) = Uελατ (π/10) = 50 { 0,1 + 0,3 ημ(10 π/10 + π/2) }2 = 50 { 0,1 - 0,3 }2 = 50 0,22 = 4 J
άνω ακραία θέση της ταλάντωσης
Β3. διατήρηση ενέργειας : Uαρχ = Kτελ => Μ g L/2 + rad/s1 g L = ½ Ι(Α) ω2 =>
=> 3 . 10 . 4/2 + 0,6 . 10 . 4 = ½ . 25,6 . ω2 => 60 + 24 = 12,8 ω2 => ω = (84/12,8)½ = 2,56 rad/s το σύστημα ράβδος - σφαιρίδιο m1 έχει γωνιακή ταχύτητα ω = 2,56 rad/s τη στιγμή που η ράβδος περνά από την κατακόρυφη θέση
η γραμμική ταχύτητα του Σ1 είναι : υm1 = ω L = 2,56 rad/s 4 m = 10,24 m/s
υm1 = ω L = (21/3,2)½ 4 = (21 16/3,2)½ = (21 5)½ = 105½ m/s ( άλλος τρόπος )
η γραμμική ταχύτητα του κέντρου μάζας του συστήματος ράβδος - σφαιρίδιο m1 είναι :
υcm = ω xcm = 2,56 rad/s 7/3 m = 5,98 m/s = 6 m/s
5.
6.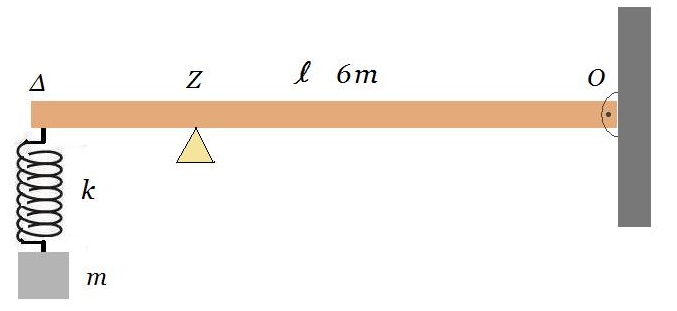
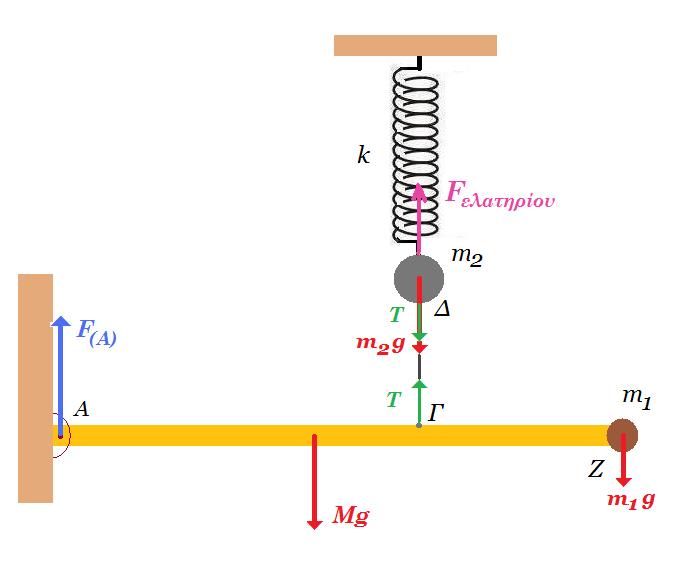
Η ράβδος OΔ του σχήματος είναι ομογενής, έχει μάζα 6m, μήκος L και συνδέεται με άρθρωση στο σημείο Ο με κατακόρυφο τοίχο. Η ράβδος μπορεί να περιστρέφεται χωρίς τριβές σε κατακόρυφο επίπεδο, γύρω από τον οριζόντιο άξονα που διέρχεται από το άκρο Ο.
Η ράβδος ισορροπεί οριζόντια με τη βοήθεια του στηρίγματος στο σημείο Ζ, ενώ στο άκρο της Δ είναι συνδεδεμένο ιδανικό ελατήριο με σταθερά Κ. Στο κάτω άκρο του ελατηρίου είναι δεμένο σώμα με μάζα m, το οποίο εκτελεί κατακόρυφη απλή αρμονική ταλάντωση. Ποια είναι η μέγιστη ταχύτητα του σώματος m, ώστε κατά τη διάρκεια της ταλάντωσής του η ράβδος ΟΔ να μην ανατρέπεται;
ροπές ως προς Ο : Fελατ l = 6m g l/2 => Fελατ = 3mg => k x1 = 3mg => x1 = 3mg/k
η μέγιστη συσπείρωση του ελατηρίου για να μην ανατραπεί η ράβδος
ισορροπία σώματος : m g = k x0 => x0 = mg/k επιμήκυνση ελατηρίου
το μέγιστο πλάτος ασφαλούς ταλάντωσης : Αmax = x0 + x1 = mg/k + 3mg/k = 4mg/k
x = A ημωt v = Aω συνωt υmax = Amax ω = 4mg/k (k/m)½ = 4 g(m/κ)½
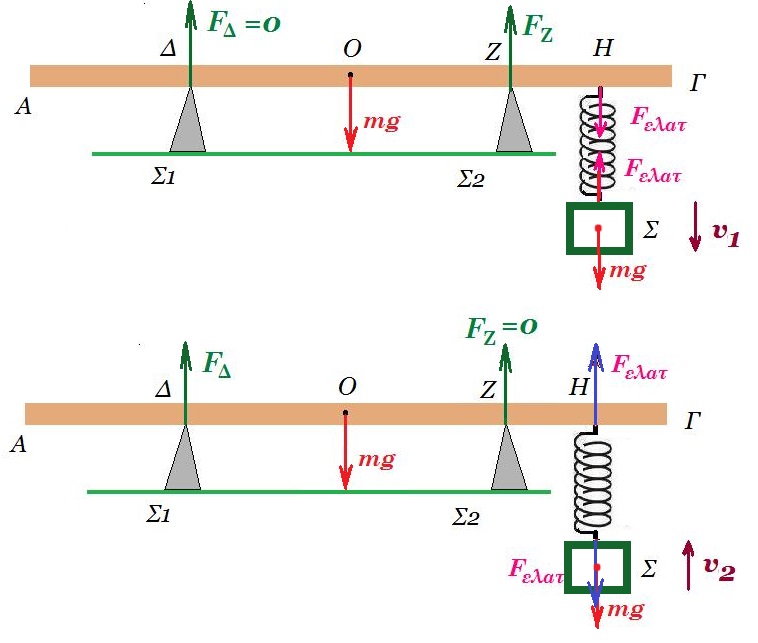
7. Ομογενής δοκός ΑΓ μικρού πάχους, μάζας m και μήκους (ΑΓ) = l ισορροπεί οριζόντια. Η δοκός ακουμπά σε δύο μυτερά στηρίγματα (Σ1) και (Σ2) στα σημεία Δ και Ζ αντίστοιχα, τα οποία απέχουν από τα άκρα της δοκού αποστάσεις (ΑΔ)=l /4 και (ΖΓ)=l /4. Από τα στηρίγματα η δοκός δέχεται κατακόρυφες δυνάμεις. Από σημείο Η της δοκού που απέχει από το άκρο Γ απόσταση (ΓΗ)=l /8, κρέμεται κατακόρυφο ιδανικό ελατήριο σταθεράς K, στο κάτω άκρο του οποίου είναι στερεωμένο και ισορροπεί μικρό σώμα (Σ) ίδιας μάζας m με τη δοκό. Το σύστημα βρίσκεται στην επιφάνεια της γης, όπου το μέτρο της επιτάχυνσης της βαρύτητας ισούται με g.
Δίνουμε στο σώμα (Σ) κατακόρυφη ταχύτητα μέτρου υ1 προς τα κάτω, οπότε καθώς κατέρχεται εκτελώντας απλή αρμονική ταλάντωση σταθεράς D=K, η δοκός οριακά δεν εκτρέπεται από την οριζόντια θέση.
Στη συνέχεια, φέρνουμε ξανά το σώμα (Σ) στη θέση ισορροπίας του, όπου ισορροπεί. Δίνουμε στο σώμα κατακόρυφη ταχύτητα μέτρου υ2 προς τα πάνω, οπότε καθώς ανέρχεται εκτελώντας απλή αρμονική ταλάντωση σταθεράς D=K, η δοκός οριακά δεν εκτρέπεται από την οριζόντια θέση. Ο λόγος υ1 / υ2 ισούται με:
α. 4/7 β. 5/7 γ. 6/7
ισορροπία Σ : m g = k d (1) όπου d = επιμήκυνση ελατηρίυ
½ k A1 2 = ½ m v12 v1 = ω Α1 Fελατ = k A1
ροπές ως προς Ζ : m g l/4 - FΔ l/2 - ( mg +Fελατ ) l/8 = 0 => m g l/4 = ( mg +Fελατ ) l/8 => m g l/8 = Fελατ l/8 => m g = k A1 = k/ω v1 (2)
½ k A2 2 = ½ m v22 v2 = ω Α2 Fελατ = k A2
ροπές ως προς Δ : m g l/4 - FΖ l/2 + mg (l/2+l/8) - Fελατ (l/2+l/8) = 0 => m g l/4 + mg 5l/8 - Fελατ 5l/8 = 0 => m g 7/8 l = Fελατ 5/8 l => 7/5 m g = k A2 = k/ω v2 (3)
(2) / (3) => υ1 / υ2 = 5/7
από (1), (2) => Α1 = d από (1), (3) => Α2 = 7/5 d
8. Οριζόντια, λεπτή ομογενής ράβδος ΟΑ μήκους L και μάζας Μ που στο άκρο της Α είναι στερεωμένη σημειακή μάζα m=M/2. Αφήνουμε το σύστημα ελεύθερο να κινηθεί χωρίς τριβές , από την οριζόντια θέση σε κατακόρυφο επίπεδο γύρω από οριζόντιο ακλόνητο άξονα που διέρχεται από το άκρο O της ράβδου.
Η ροπή αδράνειας της ράβδου ως προς άξονα που διέρχεται από το κέντρο μάζας της και είναι κάθετος σε αυτή δίνεται από τη σχέση : Icm = 1/12 M L2 και η επιτάχυνση της βαρύτητας έχει μέτρο g.
H γωνιακή επιτάχυνση του συστήματος τη στιγμή που αφέθηκε ελεύθερο έχει μέτρο:
α. αγων = 12g/L β. αγων = 3g/L γ. αγων = 6g/5L
Στ(Ο) = Ι αγων => M g L/2 + m g L = ( 1/3 Μ L2 + m L2 ) αγων =>
=> M g L/2 + M/2 g L = ( 1/3 Μ L2 + M/2 L2 ) αγων =>
=> M g L = 5/6 Μ L2 αγων => αγων = 6g/5L
9. Δύο ίδιες, λεπτές, ισοπαχείς και ομογενείς ράβδοι ΟΑ και ΟΓ, που έχουν μάζα Μ = 3 kg και μήκος l = 1 m η καθεμία, συγκολλούνται στο ένα άκρο τους Ο, ώστε να σχηματίζουν ορθή γωνία. Το σύστημα των δύο ράβδων έχει στο άκρο Α της ράβδου ΟΑ άρθρωση και ισορροπεί με τη βοήθεια αβαρούς και μη εκτατού νήματος, το οποίο σχηματίζει γωνία φ (ημφ = 0,8) με τη ράβδο ΟΓ που είναι οριζόντια. Στο άκρο Γ της ράβδου ΟΓ είναι στερεωμένο το ένα άκρο κατακόρυφου ιδανικού ελατηρίου σταθεράς k = 50 Ν/m. Στο άλλο άκρο του ελατηρίου έχει δεθεί σώμα Σ μάζας m = 0,5 kg. Το ένα άκρο του νήματος είναι δεμένο στο σημείο Ζ, το οποίο απέχει οριζόντια απόσταση l/4 από το σημείο συγκόλλησης Ο και το άλλο άκρο του είναι στερεωμένο στην οροφή.
Δ1. Να υπολογίσετε το μέτρο της τάσης του νήματος και τη δύναμη που δέχεται η ράβδος ΟΑ από την άρθρωση Α.
Απομακρύνουμε το σώμα Σ κατά μήκος του άξονα του ελατηρίου προς τα πάνω μέχρι το ελατήριο να συσπειρωθεί κατά Δl = 0,1 m και τη χρονική στιγμή t = 0 τ’ αφήνουμε ελεύθερο να κινηθεί.
Δ2. Να γράψετε τη χρονική εξίσωση της απομάκρυνσης του σώματος από τη θέση ισορροπίας της ταλάντωσης, της κινητικής ενέργειας του σώματος, της δυναμικής ενέργειας της ταλάντωσης, του ρυθμού μεταβολής της κινητικής ενέργειας, της τάσης του νήματος στο σημείο Ζ. Ποιά είναι η μικρότερη και μεγααλύτερη τιμή της τάσης του νήματος και πότε συμβαίνει αυτό;
Δ3. Να βρείτε για ποιες τιμές του πλάτους της ταλάντωσης του σώματος Σ το νήμα θα παραμείνει τεντωμένο.
Να θεωρήσετε : αμελητέες τις αντιστάσεις του αέρα, ως θετική τη φορά του βάρους.
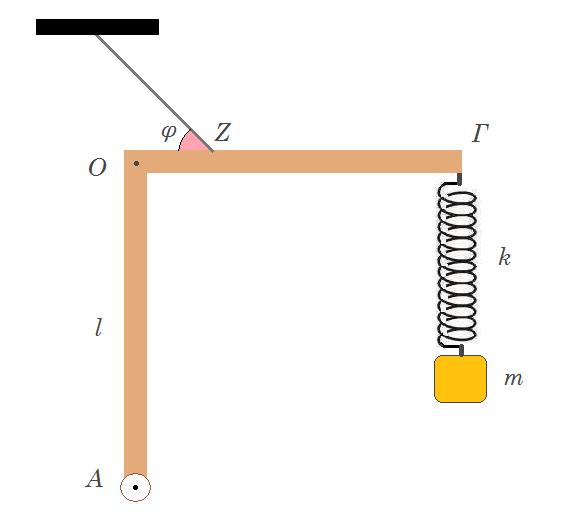
Δ1.
ισορροπία Σ : m g = Fελατ = k x0 => 0,5 10 = 50 x0 => x0 = 0,1 m επιμήκυνση
ροπές ως προς Ο : Στ(Ο) = 0 => M g l/2 + Fελατ l - Ty l/4 - Fx,A l = 0 =>
=> M g l/2 + m g l - Τ ημφ l/4 - Fx,A l = 0 =>
=> 3 10 /2 + 0,5 10 = T 0,8 /4 + Fx,A => T + 5 Fx,A = 100 (1)
ΣFx = 0 => Tx - Fx,A = 0 => Τ συνφ = Fx,A => 0,6 Τ = Fx,A (2)
(1) (2) => Τ + 5 0,6 Τ = 100 => 4 Τ = 100 => Τ = 25 Ν (3) Fx,A = 0,6 25 = 15 Ν
ΣFy = 0 => 2 M g + Fελατ - Ty - Fy,A = 0 => 2 M g + m g - T 0,8 - Fy,A = 0 =>
=> 2 3 10 + 0,5 10 - 0,8 T - Fy,A = 0 => 0,8 T + Fy,A = 65 (4)
(4) (3) => 0,8 25 + Fy,A = 65 => Fy,A = 45 Ν Fx,A = 15 Ν
FA2 = 152 + 452 = 10 152 => FA = 15 10½ Ν
Δ2.
ω2 = k / m = 50 / 0,5 = 100 => ω = 10 rad/s T = 2π/ω = π/5 s x(t) = 0,2 ημ(10t + 3π/2)
υ(t) = 2 συν(10t + 3π/2) α(t) = - 20 ημ(10t + 3π/2) ΣF(t) = m a(t) = - 10 ημ(10t + 3π/2)
K(t) = ½ m v(t)2 = 1/4 4 συν2(10t + 3π/2) = 1 συν2(10t + 3π/2)
U(t) = ½ k x(t)2 = ½ 50 0,04 ημ2(10t + 3π/2) = 1 ημ2(10t + 3π/2)
dK/dt = m v(t) a(t) = 0,5 2 συν(10t + 3π/2) [ - 20 ημ(10t + 3π/2) ] =
= - 20 συν(10t + 3π/2) ημ(10t + 3π/2) = - 10 ημ(20t + 3π/2)
ΣF(t) = m a(t) => m g + Fελατ = m a(t) => Fελατ(t) = - 5 - 10 ημ(10t + 3π/2) = - 5 - 50 x(t)
Fελατ(0) = - 5 - 10 ημ(3π/2) = - 5 - 10 (-1) = + 5 Ν το ελατήριο αρχικά είναι συσπειρωμένο 0,1 m
FΓ = - Fελατ = 5 + 10 ημ(10t + 3π/2) = 5 + 50 x(t)
ροπές ως προς Α : Στ(Α) = 0 => M g l/2 + FΓ l - Ty l/4 - Τx l = 0 =>
=> M g /2 + 5 + 10 ημ(10t + 3π/2) - T 0,8 /4 - 0,6 Τ = 0 =>
=> 15 + 5 + 10 ημ(10t + 3π/2) = T 0,8 /4 + 0,6 Τ =>
=> 20 + 10 ημ(10t + 3π/2) = 0,8 Τ => Τ(t) = 25 + 12,5 ημ(10t + 3π/2)
t = 0 T(0) = 25 + 12,5 ημ(3π/2) = 25 - 12,5 = 12,5 Ν
t = T/4 = π/20 s T(π/20) = 25 + 12,5 ημ(10 π/20 + 3π/2) = 25 + 12,5 ημ(π/2 + 3π/2) = 25 N
μέγιστη τιμή της τάσης του νήματος στο σημείο Ζ συμβαίνει όταν :
ημ(10t + 3π/2) = +1 => 10t + 3π/2 = 2Νπ + π/2 => t = Νπ/5 - π/10
1η φορά : Ν = 1 τότε t = π/5 - π/10 = π/10 s τότε T(π/10) = 25 + 12,5 ημ(10 π/10 + 3π/2) = 25 + 12,5 ημ(π + 3π/2) = 25 + 12,5 ημ(2π + π/2) = 25 + 12,5 = 37,5 N
ελάχιστη τιμή της τάσης του νήματος στο σημείο Ζ συμβαίνει όταν :
ημ(10t + 3π/2) = -1 => 10t + 3π/2 = 2Νπ + 3π/2 => t = Νπ/5
1η φορά μετά την t0 = 0 : Ν = 1 τότε t = π/5 s τότε T(π/5) = 25 + 12,5 ημ(10 π/5 + 3π/2) = 25 + 12,5 ημ(2π + 3π/2) = 25 + 12,5 ημ(3π/2) = 25 - 12,5 = 12,5 N
Δ3.
x(t) = Α ημ(10t + 3π/2) υ(t) = 10Α συν(10t + 3π/2) α(t) = - 100Α ημ(10t + 3π/2)
ΣF(t) = m a(t) = - 50 Α ημ(10t + 3π/2)
ΣF(t) = m a(t) => m g + Fελατ = m a(t) => Fελατ(t) = - 5 - 50 Α ημ(10t + 3π/2)
FΓ = - Fελατ = 5 + 50 Α ημ(10t + 3π/2) = 5 + 50 x(t)
ροπές ως προς Α : Στ(Α) = 0 => M g l/2 + FΓ l - Ty l/4 - Τx l = 0 =>
=> M g /2 + 5 + 50Α ημ(10t + 3π/2) - T 0,8 /4 - 0,6 Τ = 0 =>
=> 15 + 5 + 50Α ημ(10t + 3π/2) = T 0,8 /4 + 0,6 Τ =>
=> 20 + 50Α ημ(10t + 3π/2) = 0,8 Τ => Τ(t) = 25 + 62,5 Α ημ(10t + 3π/2)
τη χρονική στιγμή t = 0 το ελατήριο είναι κατά το μέγιστο συσπειρωμένο και ασκεί μέγιστη δύναμη στη ράβδο στο σημείο Γ κατακόρυφα προς τα πάνω οπότε για να είναι τεντωμένο το νήμα στο σημείο Ζ :
T(0) > 0 => 25 + 62,5 Α ημ(10 0 + 3π/2) > 0 => 25 + 62,5 Α ημ(3π/2) > 0 =>
=> 25 - 62,5 Α > 0 => A < 25 / 62,5 m = 0,4 m
t = 0 20 + 50Α ημ(10t + 3π/2)= 20 + 50Α ημ(3π/2) = 20 - 50A > 0 => A < 0,4 m

10. Μια λεπτή ομογενής ράβδος ΑΒ, ηρεμεί σε λείο οριζόντιο επίπεδο, στη θέση που φαίνεται στο σχήμα. Η ράβδος που έχει μήκος ℓ = 4 m και μάζα Μ = 6 kg, μπορεί να περιστρέφεται χωρίς τριβές γύρω από κατακόρυφο άξονα z, που περνά από ένα σημείο της Ο, με (ΟΒ) = ℓ/4 και τέμνει το επίπεδο σε σημείο Ο΄. Σε μια χρονική στιγμή t0=0 ασκούνται πάνω της δυο δυνάμεις F1 και F2, σταθερού μέτρου F1 = F2 = 20 Ν, οι οποίες είναι διαρκώς κάθετες στη ράβδο. H F1 ασκείται στο άκρο Α, ενώ η F2 σε σημείο Γ, όπου (ΑΓ) = ℓ/4, όπως στο σχήμα.
Α. Τη χρονική στιγμή 𝑡1 = √7𝜋 𝑠 ≅ 4,69 𝑠 να υπολογίσετε:
Α.1. τη στροφορμή της ράβδου ως προς το σημείο Ο,
Α.2. την ταχύτητα, το μέτρο του ρυθμού μεταβολής της διεύθυνσης της ταχύτητας καθώς και την επιτρόχια επιτάχυνση του κέντρου μάζας Κ της ράβδου.
Β. Την χρονική στιγμή (𝑡1) σπάει ο άξονας περιστροφής z. Να υπολογίσετε τη χρονική στιγμή 𝑡2 = 6,31 𝑠 την ταχύτητα του άκρου Β καθώς και τη στροφορμή της ράβδου ως προς το σημείο Ο΄ του επιπέδου.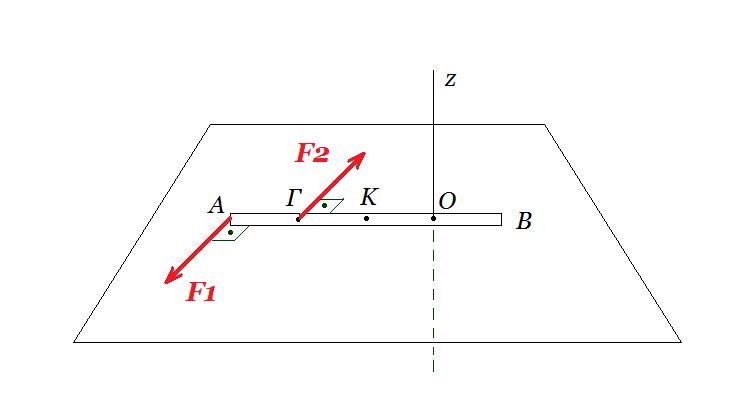
Α.
Στ(Ο) = Ι(Ο) αγων => F1 (ΟΑ) - F2 (ΟΓ) = { 1/12 Μ ℓ2 + Μ (ℓ/4)2 } αγων =>
=> F1 3ℓ/4 - F2 ℓ/2 = 7/48 Μ ℓ2 αγων => 20 3 4/4 - 20 4/2 = 7/48 6 42 αγων =>
=> 60 - 40 = 14 αγων => αγων = 10/7 rad/s2 γωνιακή επιτάχυνση της ράβδου
ω = αγων t1 = 10/7 rad/s2 4,69 𝑠 = 6,7 rad/s γωνιακή ταχύτητα της ράβδου
θ = ½ αγων t12 = ½ 10/7 rad/s (4,69 s)2 = 15,7115 rad = 5π rad
η ράβδος σε χρόνο 4,69 s κάνει 2,5 περιστροφές
L = I(O) ω = 14 6,7 = 93,8 kg m2/s
υcm = v(K) = ω (OK) => v(K) = ω ℓ/4 = 6,7 4/4 = 6,7 m/s
a(K),κεντρομόλος = v(K) 2 / ℓ/4 = 6,72 / 4/4 = 44,89 m/s2
a(K),επιτρόχιος = αγων (ΟΚ) = αγων ℓ/4 = 10/7 4/4 = 10/7 m/s2
Το άκρο Β της ράβδου έχει εκείνη τη στιγμή, ταχύτητα λόγω μεταφορικής κίνησης υcm = 6,7m/s και γραμμική ταχύτητα λόγω της κυκλικής γύρω από το Κ : v(Β)γραμ = ω (OΒ) = ω ℓ/4 = 6,7 4/4 = 6,7m/s οι δύο ταχύτητες είναι αντίρροπες μεταξύ τους
Β.
Μόλις σπάσει ο άξονας z το κέντρο μάζας Κ θα κινηθεί πλέον ευθύγραμμα, με σταθερή
ταχύτητα υcm = 6,7m/s στην διεύθυνση y, κάθετα στην αρχική διεύθυνση της ράβδου,
αφού η συνισταμένη δύναμη που δέχεται είναι μηδενική ΣF = F1 - F2 = 20 - 20 = 0 Όμως επειδή ασκείται πάνω στη ράβδο το ζεύγος δυνάμεων, θα συνεχίσει να επιταχύνεται
στροφικά εκτελώντας επιταχυνόμενη στροφική κίνηση, γύρω από κατακόρυφο άξονα ο
οποίος περνά από το μέσο της Κ (κέντρο μάζας). Ι(Κ) = 1/12 Μ ℓ2 = 1/12 6 42 = 8 kg m2
Στ(Κ) = Ι(Κ) αγων(Κ) = 1/12 Μ ℓ2 αγων(Κ) => F1 (ΚΑ) - F2 (ΚΓ) = 1/12 Μ ℓ2 αγων(Κ) =>
=> F1 ℓ/2 - F2 ℓ/4 = 1/12 Μ ℓ2 αγων(Κ) => 20 4/2 - 20 4/4 = 1/12 6 42 αγων(Κ) =>
=> αγων(Κ) = 20/8 = 2,5 rad/s2
η γωνιακή ταχύτητα της ράβδου τη στιγμή 𝑡2 = 6,31 𝑠 είναι ω2 = ωαρχ + αγων(Κ) ( 𝑡2 - 𝑡1 ) = 6,7 rad/s + 2,5 rad/s2 ( 6,31 𝑠 - 4,69 𝑠 ) => ω2 = 10,75 rad/s
η γωνιακή μετατόπιση της ράβδου είναι Δφ = ωαρχ ( 𝑡2 - 𝑡1 ) + ½ αγων(Κ) ( 𝑡2 - 𝑡1 )2 = 6,7 1,62 + ½ 2,5 1,622 = 10,854 + 3,2805 = 14,1345 rad => Δφ = 4,5 π rad
Το άκρο Β της ράβδου έχει εκείνη τη στιγμή, ταχύτητα λόγω μεταφορικής κίνησης υcm = 6,7m/s και γραμμική ταχύτητα λόγω της κυκλικής γύρω από το Κ : v(Β)γραμ = ω2 (ΚΒ) = ω2 ℓ/2 = 10,75 4/2 = 21,5 m/s οι δύο ταχύτητες είναι κάθετες μεταξύ τους
συνολικά υ(Β)2 = 6,72 + 21,52 => υ(Β) = 22,52 m/s εφθ = 6,7 / 21,5 = 0,311
Η στροφορμή στερεού που εκτελεί σύνθετη επίπεδη κίνηση, ως προς οποιοδήποτε σημείο του επιπέδου κίνησης ή κατά άξονα κάθετο σε αυτό, μπορεί να υπολογιστεί ως άθροισμα της στροφορμής λόγω ιδιοπεριστροφής, με μέτρο Lcm = Icm ω και της τροχιακής στροφορμής, με μέτρο Lτροχ = M υcm r, της στροφορμής δηλαδή του κέντρου μάζας ως προς το σημείο ή τον άξονα αναφοράς
Lcm = Icm ω2 = 8 10,75 = 86 kg m2 / s
Lτροχ = M υcm r = M υcm ℓ/4 = 6 6,7 4/4 = 40,2 kg m2 / s
LΟ = Lcm + Lτροχ = 86 kg m2 / s + 40,2 kg m2 / s = 126,2 kg m2 / s 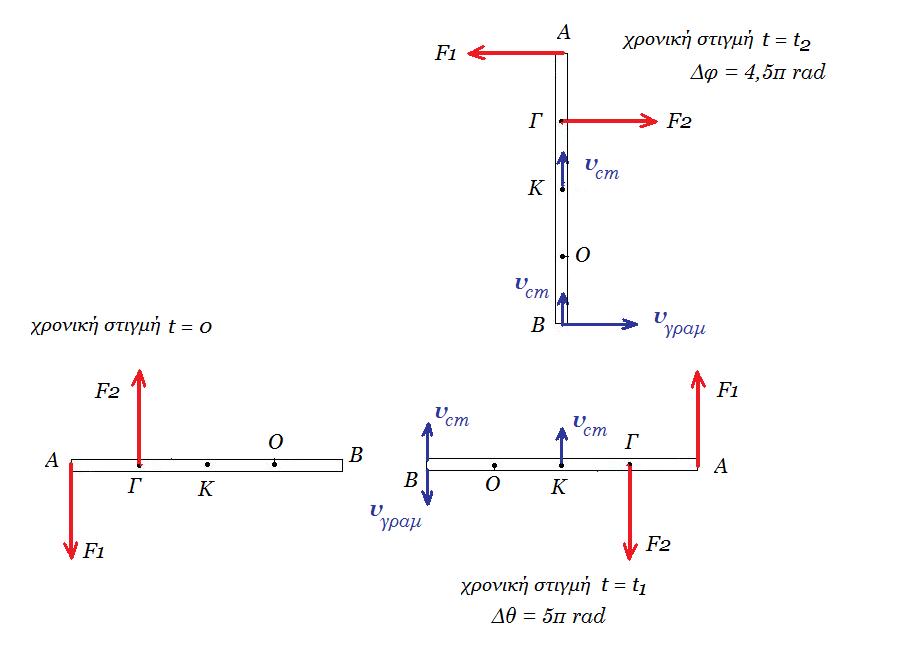
11. Ομογενής ράβδος ΟΓ μήκους l=3m και μάζας Μ=2kg ισορροπεί οριζόντια με τη βοήθεια νήματος που είναι δεμένο στο κέντρο της Κ. Το νήμα σχηματίζει με τη ράβδο γωνία φ=30° ενώ το άκρο Ο συνδέεται στον τοίχο μέσω άρθρωσης. Στο άκρο Γ είναι δεμένο ελατήριο σταθεράς k=100Ν/m που στο άλλο του άκρο έχει δεθεί σώμα μάζας m=1kg και ισορροπεί.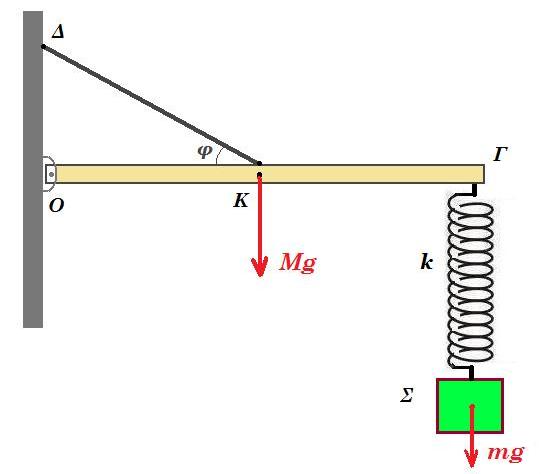 Δίνουμε στο σώμα m στη θέση ισορροπίας της αρχική ταχύτητα υ0=2m/s με φορά προς τα κάτω οπότε το σύστημα της μάζας και του ελατηρίου αρχίζει να κάνει ΑΑΤ. Το όριο θραύσης του νήματος είναι Τθ=120Ν. Να υπολογιστούν:
Δίνουμε στο σώμα m στη θέση ισορροπίας της αρχική ταχύτητα υ0=2m/s με φορά προς τα κάτω οπότε το σύστημα της μάζας και του ελατηρίου αρχίζει να κάνει ΑΑΤ. Το όριο θραύσης του νήματος είναι Τθ=120Ν. Να υπολογιστούν:
Α. Το μέτρο της τάσης του νήματος Τ, όταν το σύστημα μάζα - ελατήριο ισορροπεί.
Β. Η εξίσωση απομάκρυνσης των ταλαντώσεων της μάζας m, σε σχέση με το χρόνο, αν θεωρηθεί ως t0=0 η χρονική στιγμή που ξεκίνησε η μάζα m με ταχύτητα υ0=2m/s και θετική η φορά προς τα κάτω.
Γ. Η χρονική στιγμή t που θα κοπεί το νήμα.
Δ. Η ταχύτητα της μάζας m τη στιγμή που κόβεται το νήμα.
Ε. Ο ρυθμός μεταβολής της στροφορμής όλου του συστήματος τη στιγμή αμέσως μετά το κόψιμο του νήματος. Δίνεται g=10m/s2.

Α. ισορροπία σώματος : ΣF = 0 => mg = Fελατ = k x0 => x0 = 10/100 = 0,1 m επιμήκυνση ελατηρίου
ισορροπία ράβδου :
ροπές ως προς Ο : Στ(Ο) = 0 => Mg l/2 + k x0 l - T ημ30° l/2 = 0 => Mg /2 + k x0 = T ½ /2 => Τ = 2 Mg + 4 k x0 = 2 20 + 4 100 0,1 => Τ = 80 Ν
Β. τη στιγμή t = 0 το ελατήριο είναι επιμηκυμένο κατά 0,1 m, το σώμα έχει ταχύτητα υ0=2m/s με φορά προς τα κάτω ( θετική φορά ) και ισορροπεί
διατήρηση ενάργειας για την ταλάντωση : ½ m υ2 = ½ k Α2 => 1 22 = 100 Α2 => Α = 0,2 m πλάτος ταλάντωσης σώματος
ω2 = k / m = 100 / 1 => ω = 10 rad/s T = 2π/ω = 2π/10 = π/5 s
x(t) = 0,2 ημ10t υ(t) = 2 συν10t α(t) = - 20 ημ10t
ΣF(t) = - 20 ημ10t
ΣF(t) = - 20 ημ10t => mg + Fελατ = - 20 ημ10t => Fελατ(t) = - 10 - 20 ημ10t
t = 0 Fελατ(0) = - 10 N δύναμη ελατηρίου με κατεύθυνση κατακόρυφη προς τα πάνω
t = T/4 = π/20 s Fελατ(π/20) = - 10 - 20 ημ10(π/20) = - 10 - 20 = - 30 N μέγιστη δύναμη ελατηρίου με κατεύθυνση κατακόρυφη προς τα πάνω, το ελατήριο είναι επιμηκυμένο κατά 0,3 m
t = 3T/4 = 3π/20 s Fελατ(3π/20) = - 10 - 20 ημ10(3π/20) = - 10 + 20 = + 10 N μέγιστη δύναμη ελατηρίου με κατεύθυνση κατακόρυφη προς τα κάτω, το ελατήριο είναι συσπειρωμένο κατά 0,1 m
Γ. Δ. FΓ = - Fελατ(t) = 10 + 20 ημ10t
ροπές ως προς Ο : Στ(Ο) = 0 => Mg l/2 + FΓ l + Ty l/2 = 0 =>
=> Ty = - Mg - 2 FΓ = - 20 - 2 ( 10 + 20 ημ10t ) = - 40 - 40 ημ10t = Ty(t)
t = 0 Ty(0) = - 40 N κατακόρυφη προς τα πάνω
το νήμα κόβεται όταν η τάση |Τ| = 120 Ν => |Ty| = |Τ| ημ30° = 120 ½ = 60 Ν
Ty = - 60 Ν => - 40 - 40 ημ10t = - 60 => ημ10t = + ½ = ημ(π/6) => t = π/60 s
δηλαδή καθώς ταλαντώνεται το σώμα τη στιγμή t = π/60 s καθώς κινείται προς τα κάτω (θετική φορά) κόβεται το νήμα
x(π/60) = 0,2 ημ10(π/60) = 0,1 m υ(π/60) = 2 συν10(π/60) = 2 3½ / 2 = 3½ m/s προς τα κάτω
Fελατ(π/60) = - 10 - 20 ημ10(π/60) = - 10 - 20 . ½ = - 20 Ν το ελατήριο είναι επιμηκυμένο κατά 0,2 m
E. τη στιγμή που κόβεται το νήμα η τάση νήματος είναι μηδέν, οι δυνάμεις στη ράβδο και στο σώμα λόγω του ελατηρίου είναι εσωτερικές του συστήματος, άρα οι εξωτερικές δυνάμεις Mg και mg κάνουν ροπή
dL/dt = Στ(Ο) = Mg l/2 + mg l = 20 3/2 + 10 3 = 60 kg m2/s2 = 60 N m

 Στον δίσκο (2) είναι τυλιγμένο αβαρές και μη εκτατό κατακόρυφο νήμα (2) που το ελεύθερο άκρο του είναι δεμένο σε σώμα Σ₂ με μάζα m₂ = 1 kg. Στο κάτω μέρος του Σ₂ είναι δεμένο ιδανικό κατακόρυφο ελατήριο σταθεράς k = 100 N/m που στο κάτω του άκρο έχει δεμένο σώμα Σ₃ με μάζα m₃ = 3 kg. Αρχικά όλα τα σώματα του συστήματος ισορροπούν ακίνητα. Την χρονική στιγμή t₀ = 0 βλήμα μάζας m = 1 kg με κατακόρυφη ταχύτητα μέτρου υ₀ και φοράς προς τα πάνω συγκρούεται
Στον δίσκο (2) είναι τυλιγμένο αβαρές και μη εκτατό κατακόρυφο νήμα (2) που το ελεύθερο άκρο του είναι δεμένο σε σώμα Σ₂ με μάζα m₂ = 1 kg. Στο κάτω μέρος του Σ₂ είναι δεμένο ιδανικό κατακόρυφο ελατήριο σταθεράς k = 100 N/m που στο κάτω του άκρο έχει δεμένο σώμα Σ₃ με μάζα m₃ = 3 kg. Αρχικά όλα τα σώματα του συστήματος ισορροπούν ακίνητα. Την χρονική στιγμή t₀ = 0 βλήμα μάζας m = 1 kg με κατακόρυφη ταχύτητα μέτρου υ₀ και φοράς προς τα πάνω συγκρούεται



























 Δίνουμε στο σώμα m στη θέση
Δίνουμε στο σώμα m στη θέση 