ΘΕΜΑ Γ  2020

Δύο παράλληλοι οριζόντιοι αγωγοί ΑΓ και ΔΖ μεγάλου μήκους και μηδενικής αντίστασης απέχουν μεταξύ τους απόσταση L = 1m. Τα άκρα Α και Δ
συνδέονται με αγωγό αντίστασης R₁ = 2Ω και τα άκρα Γ και Ζ με αγωγό αντίστασης R₂ = 2Ω. Ο αγωγός ΑΓ έχει λίγο πριν το τέλος του ανοιχτό διακόπτη δ,
 όπως φαίνεται στο σχήμα. Ένας άλλος αγωγός ΚΛ, με μήκος KΛ = 1m έχει αντίσταση R_ΚΛ = 3Ω και μπορεί να ολισθαίνει χωρίς τριβές, μένοντας κάθετος
και σε επαφή στα σημεία Κ και Λ με τους οριζόντιους αγωγούς ΑΓ και ΔΖ.  Ο αγωγός ΚΛ αρχικά είναι ακίνητος.   Κάποια χρονική στιγμή, την οποία
θεωρούμε ως t=0, ασκούμε στο μέσο του αγωγού ΚΛ σταθερή δύναμη μέτρου  F = 0,8N,  η οποία είναι κάθετη στον αγωγό και η διεύθυνσή της ανήκει στο
επίπεδο που ορίζουν οι αγωγοί ΑΓ και ΔΖ.   Ο αγωγός ΚΛ αρχίζει να κινείται μέσα σε ομογενές μαγνητικό πεδίο έντασης  B₁ = 1T, που είναι κάθετο στο
επίπεδο των αγωγών ΑΓ και ΔΖ, με φορά από τον αναγνώστη προς τη σελίδα. 
Τη χρονική στιγμή t₁  ο αγωγός ΚΛ, έχοντας αποκτήσει σταθερή οριακή ταχύτητα υ_ορ , εξέρχεται από την περιοχή όπου η ένταση του μαγνητικού πεδίου
είναι Β₁ και εισέρχεται σε περιοχή, όπου η ένταση του μαγνητικού πεδίου είναι Β₂ = 0, όπως φαίνεται στο σχήμα.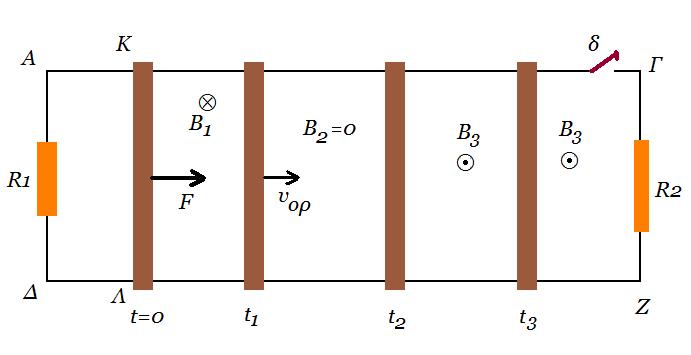

Γ1.   Να περιγράψετε το είδος της κίνησης που εκτελεί ο αγωγός ΚΛ από τη χρονική στιγμή t=0 έως τη χρονική στιγμή t₁   και να υπολογίσετε τη σταθερή οριακή ταχύτητα  υ_ορ.
Τη χρονική στιγμή t₁ καταργούμε τη δύναμη F και τη χρονική στιγμή t₂  ο αγωγός ΚΛ εισέρχεται σε περιοχή όπου υπάρχει ομογενές μαγνητικό πεδίο
έντασης Β₃, ίδιου μέτρου και αντίθετης κατεύθυνσης με την ένταση Β₁.
Γ2.   Να υπολογίσετε το μέτρο και να προσδιορίσετε τη φορά της εξωτερικής δύναμης  F ' , που πρέπει να ασκήσουμε στο μέσον του αγωγού ΚΛ, κάθετα
σε αυτόν και της οποίας η διεύθυνση ανήκει στο επίπεδο των αγωγών, ώστε ο αγωγός να συνεχίσει να κινείται με σταθερή ταχύτητα μέτρου υ_ορ .
Γ3.   Να υπολογίσετε τη θερμότητα Q, που εκλύεται στους αγωγούς του κυκλώματος από τη χρονική στιγμή t₂  μέχρι μια άλλη χρονική στιγμή t₃, αν
το επαγωγικό φορτίο που πέρασε από μία διατομή του αγωγού ΚΛ στο αντίστοιχο χρονικό διάστημα  (t₂ - t₃)  είναι  q_επ = 0,2 C.

Τη χρονική στιγμή t₃  κλείνουμε το διακόπτη δ και ο αγωγός ΚΛ, με την επίδραση της εξωτερικής δύναμης  F ' , συνεχίζει την κίνησή του στην περιοχή όπου
υπάρχει το ομογενές μαγνητικό πεδίο έντασης Β₃ και τελικά αποκτά νέα οριακή ταχύτητα.
Γ4.   Να υπολογίσετε τη νέα οριακή ταχύτητα  υ_ορ, που αποκτά ο αγωγός, καθώς και την τάση V_ΚΛ στα άκρα του αγωγού ΚΛ  και τις εντάσεις των ρευμάτων, που διαρρέουν τους αντιστάτες R₁ και R₂ , όταν αυτός κινείται με τη νέα του οριακή ταχύτητα.

Γ1.    H ράβδος  ΚΛ  κινείται μέσα σε μαγνητικό πεδίο,  τα ηλεκτρόνια της ράβδου δέχονται δύναμη Lorenz  και κινούνται προς το άκρο  Λ  το οποίο φορτίζεται αρνητικά  ενώ το άκρο  Κ  φορτίζεται θετικά.  Αναπτύσσεται τάση από επαγωγή στα άκρα της ράβδου,  Ε_επαγ  =  Β₁ . υ . l  (1)       Έχουμε κλειστό κύκλωμα :      Ε_επαγ = i . ( R₁ + R_ΚΛ )   (2)         Η ράβδος διαρρέεται από ρεύμα μέσα σε μαγνητικό πεδίο, οπότε δέχεται δύναμη Laplace :   F_L  =  i .B₁ . l   (3)    

    (1) , (2) , (3)  =>   F_L  =  i .B₁ . l  =  Ε_επαγ / ( R₁ + R_ΚΛ ) . Β₁ . l   = Β₁ . υ . l / ( R₁ + R_ΚΛ ) . Β₁ . l   =>   F_L  =  Β₁² . l² . υ / ( R₁ + R_ΚΛ )   (4)               

  Η ράβδος κινείται :   ΣF  =  m.a  =>  F - F_L  =  m.a   H επιτάχυνση της ράβδου μειώνεται συνέχεια και κάποια στιγμή μηδενίζεται, τότε :  

         F - F_L  = 0  =>  F  =  F_L =  Β₁² . l² . υ / ( R₁ + R_ΚΛ )  =>   F .( R₁ + R_ΚΛ ) / (Β₁ .l)²  =  υ   =  υ_ορ   οριακή ταχύτητα ράβδου 

       υ_ορ  =  F .( R₁ + R_ΚΛ ) / (Β₁ .l)²  =     0,8 .( 2 + 3 ) / (1 .1)²   =  4 m/s  = υ_ορ     στην περιοχή όπου Β₂ = 0   η ράβδος κινείται με σταθερή ταχύτητα  4 m/s  

Γ2.    H ράβδος  όταν εισέρχεται στην περιοχή Β₃ (αντίθετο του Β₁)  δέχεται μόνο τη δύναμη Laplace  οριζόντια προς τα αριστερά  λόγω κλειστού κυκλώματος  αφού η F  καταργείται.  Για να διατηρείται η ταχύτητα σταθερή πρέπει να ασκηθεί  F '  αντίθετη της δύναμης Laplace :   F' =  F_L =  Β₁² . l² . υ_ορ / ( R₁ + R_ΚΛ ) = 1 . 1 . 4 / (2 + 3)  =  0,8 Ν  προς τα δεξιά

Γ3.    Από τη ράβδο περνά φορτίο q_επ = 0,2 C.     q_επ =  i . Δt

1oς τρόπος     Ε_επαγ  =  B₃ . l . υ_ορ =  i .( R₁ + R_ΚΛ )  =>    B₃ . l . υ_ορ /( R₁ + R_ΚΛ )  =  i   =>   1. 1. 4 / 5 =  i   =>  i = 0,8 A  

                      q_επ =  i . Δt   => 0,2  =  0,8 . Δt  =>   Δt  =  0,2/0,8  =  0,25 sec             η ράβδος σε χρόνο 0,25 sec  διανύει απόσταση Δx = υ_ορ . Δt  =  4 m/s .0,25 s = 1 m

                     Q_θερμ = i² .( R₁ + R_ΚΛ ). Δt   =   0,8² . 5 . 0,25  =  0,8 Joule

2oς τρόπος    Ε_επαγ  = ΔΦ/Δt   =>   B₃ . l . υ_ορ =  ΔΦ/Δt   =>   i .( R₁ + R_ΚΛ )  = B₃ .ΔA/Δt  =>   i .Δt .( R₁ + R_ΚΛ )  = B₃ .Δx.l  =>

                                =>    q_επ .( R₁ + R_ΚΛ )  = B₃ .Δx.l    =>   q_επ .( R₁ + R_ΚΛ ) / B₃.l  =  Δx  =>     0,2 .( 2 + 3 ) / 1.1  =  Δx  =  1 m  η ράβδος διανύει απόσταση 1 m.

                     Q_θερμ = F_L . Δx  =  0,8 N . 1 m = 0,8 J

Γ4.   Έχουμε κλειστό κύκλωμα  R₁ , R₂  παράλληλη σύνδεση  R_1,2 = R₁ . R₂ / (R₁+R₂)  =  1 Ω 

Η ράβδος κινείται μέσα στο μαγνητικό πεδίο  Β₃  δέχεται δύναμη Laplace     ΣF  =  m.a  =>  F - F_L  =  m.a   H επιτάχυνση της ράβδου μειώνεται συνέχεια και κάποια στιγμή μηδενίζεται, τότε :           F - F_L  = 0  =>  F' =  F_L =  Β₃² . l² . υ / ( R₁ + R_ΚΛ )  =>   F' .( R_1,2 + R_ΚΛ ) / (Β₃ .l)²  =  υ   =  υ'_ορ   οριακή ταχύτητα ράβδου 

       υ'_ορ  =  F' .( R_1,2 + R_ΚΛ ) / (Β₃ .l)²  =  0,8 .( 1 + 3 ) / (1 .1)²  =  3,2 m/s  = υ'_ορ        

τότε  Ε'_επαγ  =  Β₃ . l .υ'_ορ   =  1 . 1. 3,2 =  3,2 Volt        

i' = Ε'_επαγ / ( R_1,2 + R_ΚΛ )  =  3,2 / 4 = 0,8 A    επαγωγικό ρεύμα

V_ΛΚ  =   Ε'_επαγ  -   i' . R_ΚΛ  =   3,2  -  0,8 A . 3 Ω  =   3,2 - 2,4   =  0,8 Volt

i'₁  = V_ΛΚ  / R₁  =  0,8 / 2 = 0,4 A      &      i'₂  = V_ΛΚ  / R₂  =  0,8 / 2 = 0,4 A