Θέμα   

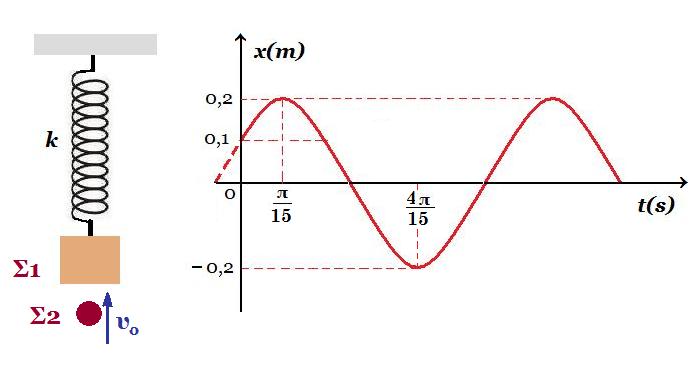Στο σχήμα δείχνεται ένα σώμα Σ₁, μάζας Μ, που είναι δεμένο στο κάτω άκρο κατακόρυφου ιδανικού ελατηρίου σταθεράς k = 100 N/m   του οποίου το άλλο άκρο είναι ακλόνητα στερεωμένο σε οροφή.
Ένα δεύτερο σώμα Σ₂, μάζας m, κινούμενο κατακόρυφα προς τα πάνω προσπίπτει με ταχύτητα μέτρου υ_ο στο αρχικά ακίνητο σώμα Σ₁. Τα δύο σώματα συγκρούονται πλαστικά και ακαριαία τη χρονική στιγμή t=0s.
Μετά την κρούση το δημιουργούμενο συσσωμάτωμα εκτελεί απλή αρμονική ταλάντωση, με την απομάκρυνση του συσσωματώματος από τη θέση ισορροπίας του να μεταβάλλεται με τον χρόνο όπως στο διάγραμμα.    Να υπολογίσετε :

Γ1.    τη μάζα, m, του σώματος Σ₂  

Γ2.   τη μάζα, M, του σώματος Σ₁

Γ3.   το μέτρο της ταχύτητας του σώματος Σ₂, ελάχιστα πριν την κρούση 

Γ4.   το έργο της δύναμης του ελατηρίου από την στιγμή της κρούσης μέχρι την στιγμή  3π/15 s  
Δίνεται g=10 m/s²    

ισορροπία Σ₁  :   M . g  =  k . x₁  =>  x₁  =  M.g/k    (1)

ισορροπία συσσωματώματος :   (M + m) . g  =  k . x₂  =>  x₂  =  (M+m).g/k    (2)

από το διάγραμμα έχουμε   πλάτος ταλάντωσης  Α = 0,2m,    x(0) = 0,1 m,  

                 T/2 = 4π/15 - π/15 = 3π/15 = π/5 s  =>  T = 2π/5 s       οπότε  ω = 2π/Τ = 5 rad/s  

        k = (M + m) . ω²  =>   100 = (M + m) . 25  =>   M + m = 4 kg    (3) 

    (3), (2)  =>    x₂  =  (M+m).g/k  =   4 . 10 / 100  =>  x₂  =  0,4 m     επιμήκυνση ελατηρίου στη θέση ισορροπίας του συσσωματώματος  

   επειδή    x(0) = 0,1 m  σημαίνει ότι το συσσωμάτωμα βρίσκεται 0,1 m  πάνω από τη θέση ισορροπίας του   δηλαδή   x₂ - x₁ = 0,1 m  =>    0,4 m - x₁ = 0,1 m  =>  x₁ = 0,3 m

  από τη σχέση (1) =>   x₁  =  M.g/k  =>  Μ = k.x₁ / g  =  100 . 0,3 / 10 =  3 kg  =>  M = 3 kg   οπότε  m = 1 kg 

  θετική κατεύθυνση προς τα πάνω     x(t)  =  0,2 . ημ(5.t + π/6)     διότι :   x(0)  =  0,2 . ημ(π/6) = 0,2 . ½ = 0,1m             v(t) = 1 . συν(5.t + π/6)       α(t)  =  -5 . ημ(5.t + π/6) 

        v(0) = 1 . συν(π/6)  =  Φ3/2 m/s       το μέτρο της ταχύτητας του συσσωματώματος  όταν αρχίζει την ταλάντωση  δηλαδή  αμέσως μετά την κρούση

  διατήρηση ορμής κατά την κρούση :    m . υ₀  =  (m + M) . v  =>   1 . υ₀  =  4 . Φ3/2   =>   υ₀  =  2ΧΦ3 m/s   το μέτρο της ταχύτητας του Σ₂  ελάχιστα πριν την κρούση   

  δύναμη ελατηρίου   ΣF  =  - D . x(t)   =>  F_ελατ  -  (m + M).g  =  - k . x(t)  =>    F_ελατ  =  (m + M).g  - k . x(t)  =>  

                                                                     =>  F_ελατ  = k . x₂ - k . x(t)  =>   F_ελατ  =  40  - 100 . 0,2 . ημ(5.t + π/6)  =>  

           F_ελατ(t)  =  40  -  20 . ημ(5.t + π/6)          F_ελατ(0)  =  40  -  20 . ημ(π/6)  =  40  -  10  =  30 N  =  k . x₁    

      U_ελατ(t)  =   ½ . k . { x₂ - x(t) }²   =    ½ . 100 . { 0,4  -  0,2.ημ(5.t + π/6) }²   =>

                                                       =>   U_ελατ(t)  =  50 . { 0,4  - 0,2.ημ(5.t + π/6) }²          

   U_ελατ(0)  =  50 . { 0,4  - 0,2.ημ(π/6) }²  =  50 . { 0,4  - 0,2.(½) }²   =  50 . { 0,4  -  0,1 }²   =  50 . 0,3²  =  4,5 Joule

   U_ελατ(π/5)  =  50 . { 0,4  - 0,2.ημ(5.π/5 + π/6) }²  =  50 . { 0,4  - 0,2.(-½) }²  =  50 . { 0,4  +  0,1 }²   =  12,5 Joule

 μεταβολή δυναμικής ενέργειας ελατηρίου :  ΔU_ελατ  =   U_ελατ(π/5)  -  U_ελατ(0)  =  12,5 J  -  4,5 J  =  8 Joule