
ΘΕΜΑ Δ
Η διπλή τροχαλία του σχήματος με ακτίνες r1 και r2 = 3r1, μπορεί να στρέφεται χωρίς τριβές γύρω από οριζόντιο άξονα περιστροφής, που διέρχεται από το κέντρο της. Η τροχαλία έχει αμελητέα μάζα, δηλαδή κάθε στιγμή ισχύει για αυτήν ότι το άθροισμα των ροπών που της ασκούνται ως προς τον άξονα περιστροφής της είναι ίσο με μηδέν, είτε ισορροπεί, είτε περιστρέφεται. Γύρω από το εξωτερικό αυλάκι της τροχαλίας υπάρχει τυλιγμένο ένα αβαρές και μη εκτατό νήμα, στο άκρο του οποίου είναι δεμένο ένα σώμα Σ2 μάζας m. Στο εσωτερικό αυλάκι της τροχαλίας είναι επίσης τυλιγμένο ένα αβαρές και μη εκτατό νήμα, το άκρο του οποίου είναι δεμένο στο μέσο μιας ομογενούς μεταλλικής ράβδου, ΚΛ, μήκους l , αντίστασης R3 και μάζας M, η οποία μπορεί να κινείται πάνω στους οριζόντιους, αγώγιμους – αμελητέας αντίστασης - οδηγούς Αx και Γx’.
Στο χώρο υπάρχει κατακόρυφο ομογενές μαγνητικό πεδίο έντασης Β με τη φορά των δυναμικών γραμμών προς τα κάτω. Τα σημεία του κυκλώματος Α, Γ συνδέονται μέσω του μεταγωγού δ, είτε με ηλεκτρική πηγή ΗΕΔ Ε = 9 V και εσωτερικής αντίστασης R1, είτε με αντίσταση R2. Στην αρχή ο μεταγωγός δ βρίσκεται στη θέση Ζ και η ράβδος ισορροπεί.
Δ1. Να μελετήσετε την ισορροπία της μεταλλικής ράβδου ΚΛ.
Δ2. Την χρονική στιγμή t=0 φέρνουμε τον μεταγωγό δ στη θέση Ε και η ράβδος αρχίζει να κινείται πάνω στους οδηγούς. Μελετήστε την κίνηση της ράβδου και του σώματος Σ2.
Δ3. Να υπολογίσετε την τάση στα άκρα του αντιστάτη R2 την χρονική στιγμή που το σώμα Σ2 κατέρχεται με επιτάχυνση α2 = 3 m/s2.
Δ4. Να υπολογίσετε την μέγιστη – οριακή – ταχύτητα υορ που θα αποκτήσει το σώμα Σ2.
Δ5. Για το χρονικό διάστημα που απαιτείται για να κάνει η τροχαλία 9 στροφές μετά από την χρονική στιγμή που το σώμα Σ2 αποκτά την μέγιστη – οριακή – ταχύτητα, να υπολογίσετε τη μείωση της δυναμικής ενέργειας του σώματος Σ2 και να επιβεβαιώσετε την ισχύ της αρχής διατήρησης της ενέργειας. Δίνεται g=10 m/s2

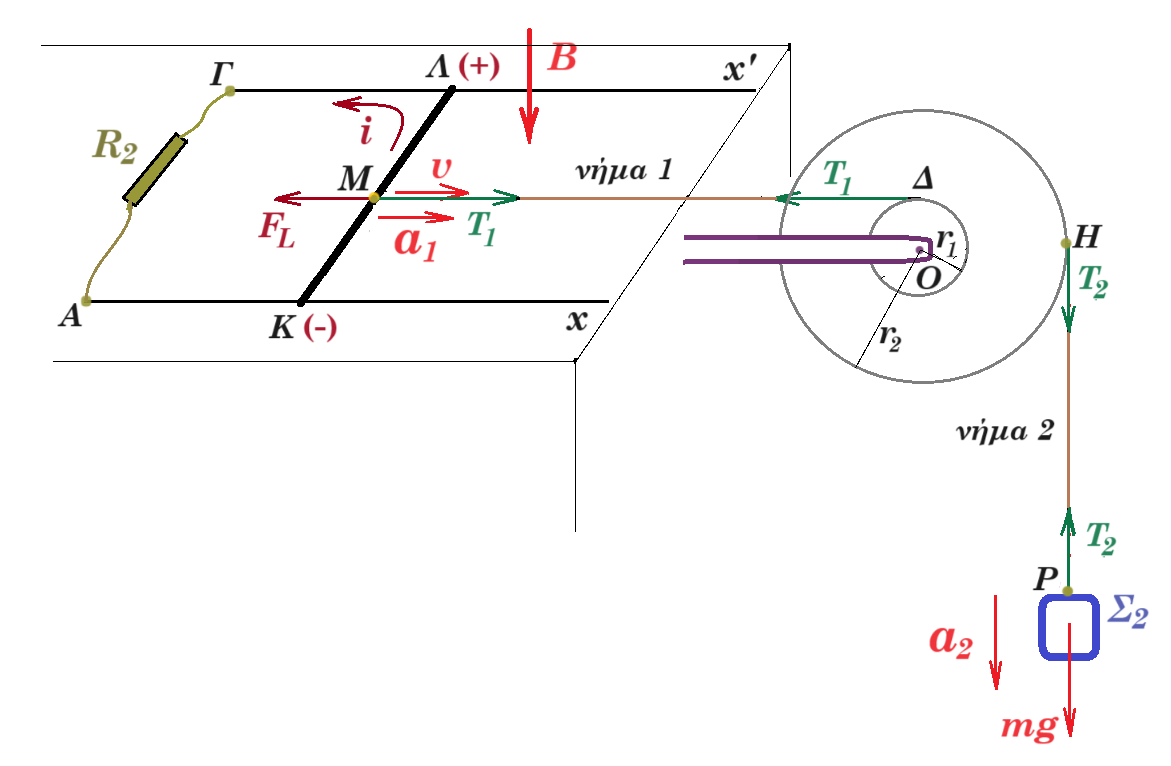
ισορροπία Σ2 : mg = T2 = 5 N
ροπές ως προς το κέντρο Ο της τροχαλίας : Στ(Ο) = 0 => T1 r1 - T2 r2 = 0 => T1 r1 - T2 3r1 = 0 =>
=> T1 = 3T2 = 3mg
νόμος του Ohm για κλειστό κύκλωμα : Ε = i (R1 + R3) => i = Ε / (R1 + R3)
ισορροπία ράβδου ΚΛ : Τ1 - FL = 0 => T1 - B l i = 0 => 3mg = B l E / (R1 + R3)
ο μεταγωγός στη θέση Ε => το σώμα Σ2 κατέρχεται με επιτάχυνση α2 η τροχαλία περιστρέφεται με γωνιακή επιτάχυνση αγων η ράβδος κινείται με επιτάχυνση α1
α2 = α(Ρ) = α(Η) = αγων r2 = αγων 3r1 = 3 αγων r1 = 3 α(Δ) = 3 α(Μ) = 3 α1 => a2 = 3 a1 (1)
mg - T2 = m a2 (2)
Στ(Ο) = 0 => T1 r1 - T2 r2 = 0 => T1 r1 - T2 3r1 = 0 => T1 = 3T2 (3)
στα άκρα της ράβδου εμφανίζεται επαγωγική τάση Εεπαγ = B l v
νόμος του Ohm για κλειστό κύκλωμα : B l v = i (R2 + R3) => i = B l v / (R2 + R3)
η ράβδος δέχεται δύναμη Laplace : FL = B l i = B l B l v / (R2 + R3) = B2 l2 v / (R2 + R3) (4)
κίνηση ράβδου ΚΛ : Τ1 - FL = Μ α1 => T1 - B2 l2 v / (R2 + R3) = Μ α1 (5)
(5) + 3*(2) => T1 - B2 l2 v / (R2 + R3) + 3mg - 3T2 = Μ α1 + 3 m a2 =>
=> - B2 l2 v / (R2 + R3) + 3mg = Μ α1 + 3 m a2 => (1)
=> 3mg - B2 l2 v / (R2 + R3) = Μ α1 + 3 m 3 a1 =>
=> 3mg - B2 l2 v / (R2 + R3) = (Μ + 9m) a1 =>
=> 3mg - b v = (Μ + 9m) a1 b = B2l2 / (R2 + R3) θετική σταθερά
αρχικά η ράβδος είναι ακίνητη υ = 0 οπότε η σχέση : 3mg - b v = (Μ + 9m) a1 => 3mg = (Μ + 9m) a1 => a1 = 3mg/(Μ + 9m) αρχική επιτάχυνση της ράβδου
η αρχική επιτάχυνση του Σ2 είναι α2 = 3 α1 = 9mg/(Μ + 9m)
η ράβδος δέχεται δύναμη Laplace αντίρροπη της ταχύτητάς της με μέτρο ανάλογο του μέτρου της ταχύτητας
3mg - b v = (Μ + 9m) a1 => 3mg - b v = (Μ + 9m) dv/dt => - b ( v - 3mg/b ) = (M + 9m) dv/dt => dv / (v - 3mg/b) = - b / (M + 9m) dt => ln [ (v - 3mg/b) / (- 3mg/b) ] = - b / (M + 9m) t =>
=> v(t) = 3mg/b [ 1 - e - b/(M + 9m) t ] v(0) = 0 v( ¥ ) = 3mg/b
α(t) = 3mg/(M + 9m) e - b/(M + 9m) t a(0) = 3mg/(M + 9m) a( ¥ ) = 0
dx = v dt = 3mg/b [ 1 - e - b/(M + 9m) t ] dt =>
x(t) = 3mg/b t + 3mg(M + 9m)/b2 [ e - b/(M + 9m) t - 1 ]
x(0) = 0 x( t®¥ ) = 3mg/b t - 3mg(M + 9m)/b2
΄~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
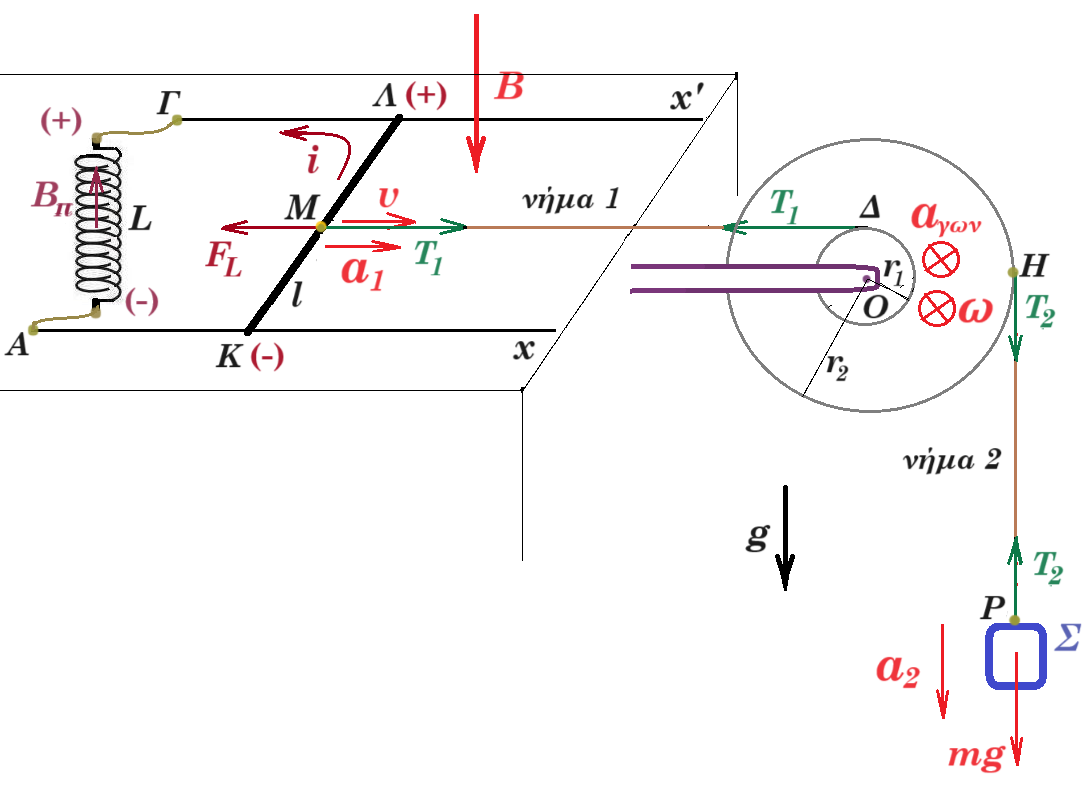
η διάταξη αφήνεται να κινηθεί οι ωμικές αντιστάσεις είναι μηδενικές
το ιδανικό πηνίο έχει συντελεστή αυτεπαγωγής L η μεταλλική ράβδος ΚΛ έχει μάζα Μ και μήκος l
το σώμα Σ έχει μάζα m η διπλή τροχαλία έχει αμελητέα μάζα και ισχύει r2 = 3r1
το σώμα Σ2 κατέρχεται με επιτάχυνση α2 η τροχαλία περιστρέφεται με γωνιακή επιτάχυνση αγων
η ράβδος κινείται με επιτάχυνση α1
α2 = α(Ρ) = α(Η) = αγων r2 = αγων 3r1 = 3 αγων r1 = 3 α(Δ) = 3 α(Μ) = 3 α1 => a2 = 3 a1 (1)
mg - T2 = m a2 (2)
Στ(Ο) = 0 => T1 r1 - T2 r2 = 0 => T1 r1 - T2 3r1 = 0 => T1 = 3T2 = 3mg - 3m a2 = 3mg - 9m a1 (3)
στα άκρα της ράβδου εμφανίζεται επαγωγική τάση Εεπαγ = B l v
στα άκρα του πηνίου εμφανίζεται τάση αυτεπαγωγής : ΕΑΥΤ = - L di/dt
νόμος του Ohm για κλειστό κύκλωμα : B l v - L di/dt = i (Rπ + R) = 0 => B l dx/dt = L di/dt =>
=> B l dx = L di => B l x = L i => i = ( B l / L ) x
η ένταση i του ρεύματος που διαρρέει το κύκλωμα είναι ανάλογη της θέσης x
η ράβδος δέχεται δύναμη Laplace : FL = B l i = B l ( B l / L ) x = (B2 l2 / L) x (4)
κίνηση ράβδου ΚΛ : Τ1 - FL = Μ α1 => T1 - (B2 l2 / L) x = Μ α1 (5)
(5) , (3) => 3mg - 9m a1 - (B2 l2 / L) x = Μ α1 => 3mg - (B2 l2 / L) x = (Μ + 9m) α1 (6)
η ράβδος διανύει χ η επιτάχυνσή της μειώνεται κάποια στιγμή μηδενίζεται οπότε η ταχύτητα της λαμβάνει σταθερή τιμή
τότε 3mg - (B2 l2 / L) χ = 0 => χ = 3mgL / B2l2
η ένταση ρεύματος Ι = ( B l / L ) χ = 3mg / Bl
στο πηνίο αποθηκεύεται ενέργεια Uπ = ½ L I2 = ½ L (3mg / Bl)2
η δύναμη Laplace γίνεται (4) => FL = B l i = B l ( B l / L ) x = (B2 l2 / L) x = (B2 l2 / L) χ = 3mg
το Σ μετατοπίζεται προς τα κάτω διανίοντας 3πλάσια απόσταση απ'ότι η ράβδος στο ίδιο χρονικό διάστημα α2 = 3 α1 => dv2/dt = 3 dv1/dt => v2 = 3 v1 => dx2/dt = 3 dx1/dt => x2 = 3 x1
άρα διανύει απόσταση 3 χ = 3 3mgL / B2l2 = 9mgL / B2l2
mg 9mgL / B2l2 = ½ 9 L m2 g2 / B2l2 + ½ Μ v12 + ½ m v22 = ½ 9 L m2 g2 / B2l2 + ½ Μ v12 + ½ m 9v12 =>
=> mg 9mgL / B2l2 = ½ 9 L m2 g2 / B2l2 + ½ (Μ + 9m) v12 =>
=> ½ 9 L m2 g2 / B2l2 = ½ (Μ + 9m) v12 => 9m2g2L / B2l2(Μ + 9m) = v12
v1 = 3mg/(Bl) (L/(M+9m)½
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
η διάταξη αφήνεται να κινηθεί οι ωμικές αντιστάσεις είναι μηδενικές
το ιδανικό ελατήριο έχει σταθερά k η μεταλλική ράβδος ΚΛ έχει μάζα Μ και μήκος l Μ μέσον ΚΛ
το σώμα Σ έχει μάζα m η διπλή τροχαλία έχει αμελητέα μάζα και ισχύει r2 = 3r1
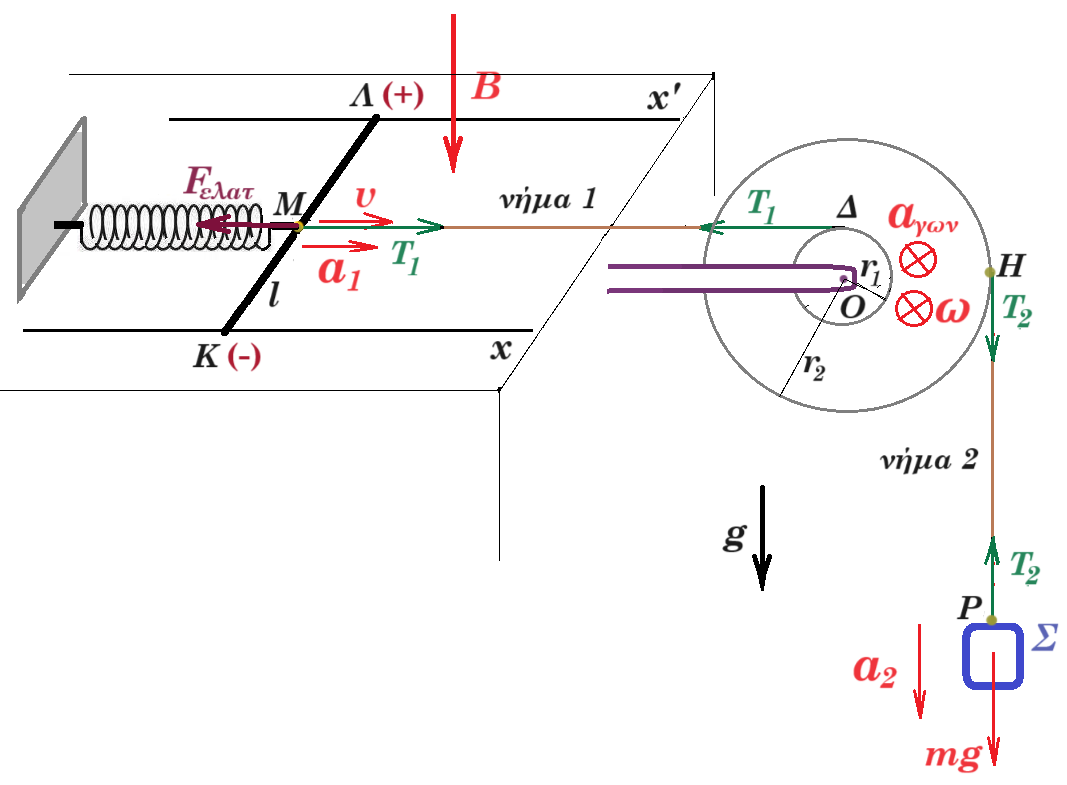 αρχικά το ελατήριο έχει το φυσικό του μήκος τη στιμή μηδέν αφήνουμε το σύστημα να κινηθεί το σώμα Σ κατέρχεται με επιτάχυνση α2 η τροχαλία περιστρέφεται με γωνιακή επιτάχυνση αγων
αρχικά το ελατήριο έχει το φυσικό του μήκος τη στιμή μηδέν αφήνουμε το σύστημα να κινηθεί το σώμα Σ κατέρχεται με επιτάχυνση α2 η τροχαλία περιστρέφεται με γωνιακή επιτάχυνση αγων
η ράβδος κινείται με επιτάχυνση α1 α2 = α(Ρ) = α(Η) = αγων r2 = αγων 3r1 = 3 αγων r1 = 3 α(Δ) = 3 α(Μ) = 3 α1 => a2 = 3 a1 (1) v2 = 3 v1 s2 = 3 s1
κίνηση σώματος Σ : mg - T2 = m a2 (2)
Στ(Ο) = 0 => T1 r1 - T2 r2 = 0 => T1 r1 - T2 3r1 = 0 => T1 = 3T2 = 3mg - 3m a2 = 3mg - 9m a1 (3)
στα άκρα της ράβδου εμφανίζεται επαγωγική τάση Εεπαγ = B l v
κίνηση ράβδου ΚΛ : Τ1 - Fελατ = Μ α1 => 3mg - 9m a1 - k x = Μ α1 => 3mg - k x = (Μ + 9m) α1 (4) όσο κινείται η ράβδος ΚΛ προς τα δεξιά το ελατήριο επιμηκύνεται οπότε το μέτρο της επιτάχυνσης μειώνεται κάποια στιγμή α1 = 0 => 3mg = k x1 => x1 = 3mg/k τότε η ταχύτητα της ράβδου είναι μέγιστη το Σ έχει κατέβει κατά h = 3x1
mg h = ½ m v22 + ½ M v12 + ½ k x12 => mg 3 3mg/k = ½ m 9v12 + ½ M v12 + ½ k (3mg/k)2 =>
=> 9 m2 g2 / k = ½ (M + 9m) v12 + ½ 9 m2 g2 / k => v12 = (3mg)2 / k(M + 9m) μέγιστη ταχύτητα
αμέσως μετά το ελατήριο επιμηκύνεται περισσότερο από x1 οπότε η δύναμη ελατηρίου είναι μεγαλύτερη από την τάση νήματος Τ1 άρα η ράβδος επιβραδύνεται μέχρι να σταματήσει έστω x2 η επιμήκυνση του ελατηρίου εκείνη τη στιγμή το Σ κατεβαίνει κατά Η = 3 x2
η δυναμική βαρυτική ενέργεια του Σ αποθηκεύεται στο ελατήριο mg Η = ½ k x22 => mg 3x2 = ½ k x22 => x2 = 6 mg/k = 2 x1
η ράβδος κάνει ΑΑΤ με πλάτος x1 = 3mg/k και μέγιστη ταχύτητα v1 = 3mg / √(k(M+3m))
v1 = ω x1 => 3mg / √(k(M+3m)) = ω 3mg/k => ω2 = k / (M+9m) κυκλική συχνότητα ταλάντωσης
mg - T2 = m a Τ1 - Fελατ = Μ α mg - k x = (M+m) a a = 0 => x1 = mg / k
mg h = ½ m v22 + ½ M v12 + ½ k x12 => mg mg/k = ½ m v12 + ½ M v12 + ½ k (mg/k)2 => (mg)2 / k = (M+m) v12 => v12 = (mg)2 / k(M+m)
mg Η = ½ k x22 => mg x2 = ½ k x22 => x2 = 2 mg/k = 2 x1
η ράβδος κάνει ΑΑΤ με πλάτος x1 = mg/k και μέγιστη ταχύτητα v1 = mg / √(k(M+m))
v1 = ω x1 => mg / √(k(M+m)) = ω mg/k => ω2 = k / (M+m) κυκλική συχνότητα ταλάντωσης
ΘΕΜΑ Δ
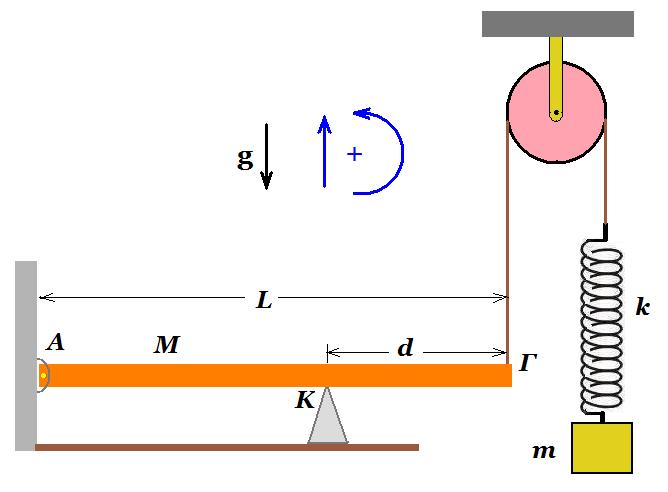 Λεπτή ομογενής ράβδος (ΑΓ) με μήκος 𝐋 = 𝟏,𝟐𝐦 και μάζα 𝚳 = 𝟒𝐤𝐠 ισορροπεί οριζόντια, αρθρωμένη στο αριστερό άκρο της (Α). Η ισορροπία της ράβδου επιτυγχάνεται με τη βοήθεια του λείου στηρίγματος (σημείο Κ) που απέχει απόσταση 𝐝 από το (Γ) και του κατακόρυφου αβαρούς, μη ελαστικού νήματος που έχουμε δέσει στο δεξιό άκρο της (Γ), όπως φαίνεται στο σχήμα.
Λεπτή ομογενής ράβδος (ΑΓ) με μήκος 𝐋 = 𝟏,𝟐𝐦 και μάζα 𝚳 = 𝟒𝐤𝐠 ισορροπεί οριζόντια, αρθρωμένη στο αριστερό άκρο της (Α). Η ισορροπία της ράβδου επιτυγχάνεται με τη βοήθεια του λείου στηρίγματος (σημείο Κ) που απέχει απόσταση 𝐝 από το (Γ) και του κατακόρυφου αβαρούς, μη ελαστικού νήματος που έχουμε δέσει στο δεξιό άκρο της (Γ), όπως φαίνεται στο σχήμα.
Το νήμα διέρχεται από το αυλάκι μόνιμα ακίνητης λείας τροχαλίας και είναι δεμένο στο πάνω άκρο κατακόρυφου ελατηρίου σταθεράς 𝐤 = 𝟏𝟎𝟎𝐍/𝐦. Στο κάτω άκρο του ελατηρίου ισορροπεί το μικρό σώμα Σ μάζας 𝐦 = 𝟏𝐤𝐠. Δίνεται η επιτάχυνση της βαρύτητας 𝐠 = 𝟏𝟎𝐦/𝐬𝟐.
Δ1. Αν οι δυνάμεις που δέχεται η ράβδος από την άρθρωση και το στήριγμα είναι ίσες να βρεθεί η απόσταση 𝐝. Μονάδες 4
Μετατοπίζουμε το σώμα μάζας 𝐦 κατακόρυφα προς τα κάτω κατά 𝟓𝐜𝐦 και το εκτοξεύουμε κατακόρυφα προς τα πάνω με ταχύτητα μέτρου 𝟎,𝟓√𝟑𝐦/𝐬.
Δ2. Να βρεθεί το πλάτος της ταλάντωσης του σώματος. Μονάδες 4
Δ3. Να βρεθούν:
α) Το μέτρο της τάσης του νήματος όταν το σώμα μάζας 𝐦 βρίσκεται στην ανώτερη θέση της τροχιάς του. Μονάδες 4
β) Το μέτρο της δύναμης που ασκεί το στήριγμα στη ράβδο όταν το σώμα μάζας 𝐦 βρίσκεται στην κατώτερη θέση της τροχιάς του. Μονάδες 4
Δ4. Να βρεθεί το μέτρο του ρυθμού μεταβολής της κινητικής ενέργειας του σώματος μάζας 𝐦 όταν η ράβδος δέχεται δύναμη μέτρου 𝟏𝟐𝚴 από την άρθρωση. Μονάδες 4
Δ5. Να εκφράσετε τις δυναμεις που δέχεται η ράβδος στα σημεία Α και Κ συναρτήσει του χρόνου και συναρτήσει της απομάκρυνσης x του σώματος Σ από την θέση ισορροπίας του καθώς αυτό ταλαντώνεται. Μονάδες 5
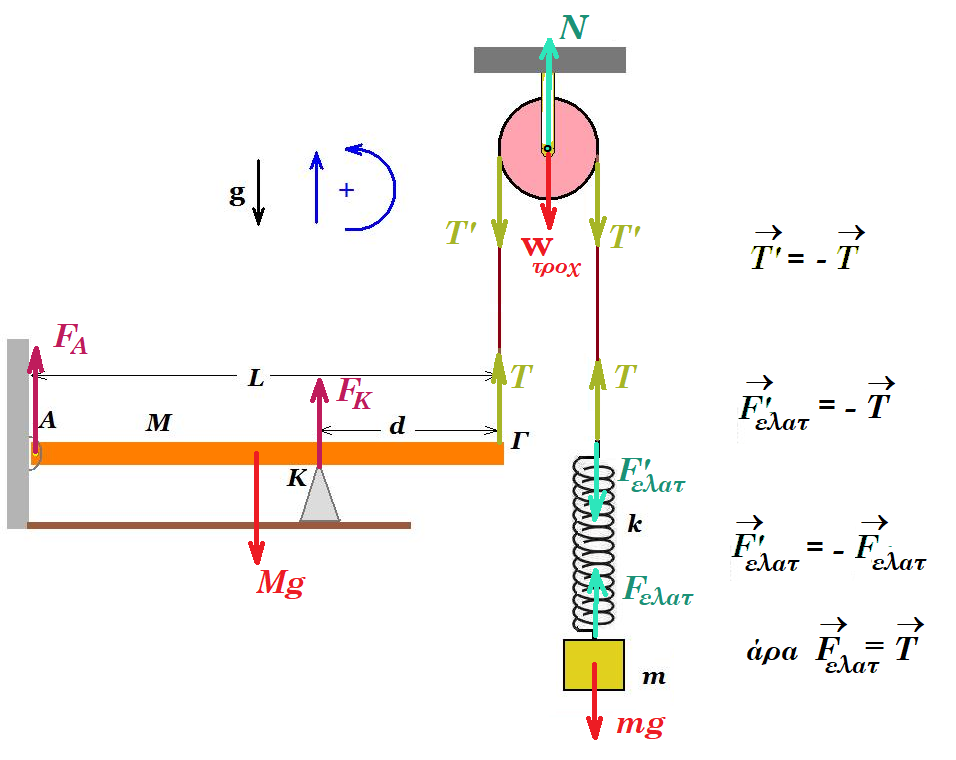
ισορροπία σώματος : mg = Fελατ = k Δl => 10 Ν = Fελατ = 100 N/m Δl => Δl = 0,1 m T = Fελατ = 10 Ν
ισορροπία ράβδου :
Στ(Κ) = 0 => Mg ( l/2 - d ) + T d - FA ( l - d ) = 0 => 40 ( 0,6 - d ) + 10 d - FA ( 1,2 - d ) = 0 (1)
Στ(A) = 0 => - Mg l/2 + T l + FK ( l - d ) = 0 => - 40 0,6 + 10 1,2 + FK ( 1,2 - d ) = 0 (2)
(2) + (1) => - 40 0,6 + 10 1,2 + FK ( 1,2 - d ) + 40 ( 0,6 - d ) + 10 d - FA ( 1,2 - d ) = 0 => FK = FA
=> 10 1,2 + 40 ( - d ) + 10 d = 0 => 12 = 30 d => d = 0,4 m
½ m v2 + ½ k x2 = ½ k A2 => 1 3 0,25 + 100 0,052 = 100 A2 => 0,75 + 0,25 = 100 A2 =>
=> 1 = 100 A2 => A = 0,1 m = Δl k = m ω2 => ω = 10 rad/s T = π/5 s
Δ3 α) όταν το σώμα βρεθεί στην ανώτερη θέση της τροχιάς του το ελατήριο θα έχει το φυσικό του μήκος άρα Fελατ=0 οπότε Τ=0
η ταχύτητα κατακόρυφη προς τα πάνω x(0) = - 0,05 m v(0) = + 𝟎,𝟓√𝟑𝐦/𝐬
x = 0,1 ημ(10t + 11π/6) υ = 1 συν(10t + 11π/6) α = - 10 ημ(10t + 11π/6)
ΣF = m α => Fελατ - mg = mα => Fελατ = mg + mα => Fελατ = 10 - 10 ημ(10t + 11π/6) = T
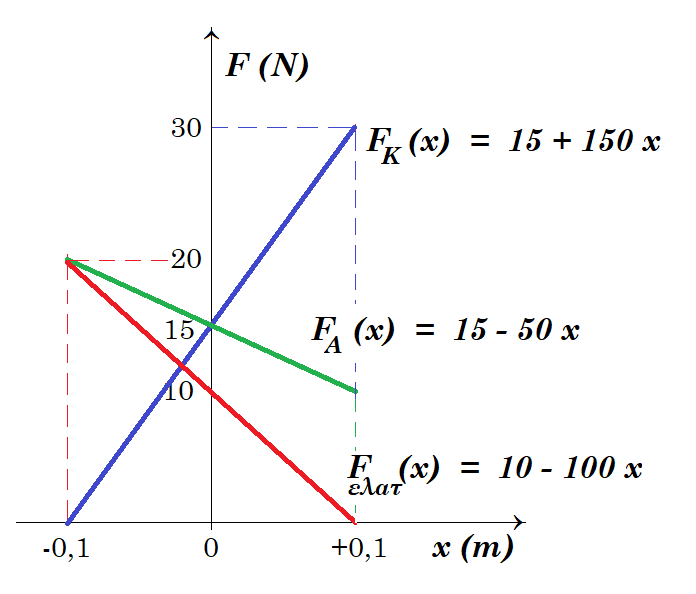
Fελατ = - k (x + x0) = - 100 (x - 0,1) = 10 - 100 x - 0,1m £ x £ + 0,1m
x = - 0,1 m Fελατ = + 20 N x = 0 m Fελατ = + 10 N x = + 0,1 m Fελατ = 0
η δύναμη που ασκείται στο σώμα από το ελατήριο είναι συνεχώς κατακόρυφη προς τα επάνω
x = 0,1 ημ(10t + 11π/6) = 0,1 => ημ(10t + 11π/6) = 1 = ημπ/2 => 10t + 11π/6 = π/2 + 2πΝ =>
=> 10t = π/2 + 2πΝ - 11π/6 => 10t = 2πΝ - 8π/6 Ν = 1 t = (2π - 4π/3) / 10 = 2π/3 / 10 = π/15 s
π/15 - π/20 = 4π/60 - 3π/60 = π/60 = π/5 / 12 = Τ / 12
t = 0 x = 0,1 ημ(11π/6) = 0,1 (- ½) = - 𝟎,𝟎𝟓𝐦 υ = 1 συν(11π/6) = 𝟎,𝟓√𝟑𝐦/𝐬
α = - 10 ημ(11π/6) = 𝟓𝐦/𝐬2 Fελατ = 10 - 10 ημ(11π/6) = 10 - (- 5) = 15 N
t = π/15 s x = 0,1 ημ(10 π/15 + 11π/6) = 0,1 ημ(4π/6 + 11π/6) = 0,1 ημ(5π/2) = 𝟎,1𝐦
υ = 1 συν(10 π/15 + 11π/6) = 1 συν(5π/2) = 𝟎
α = - 10 ημ(10 π/15 + 11π/6) = - 10 ημ(5π/2) = - 10𝐦/𝐬2
Fελατ = 10 - 10 ημ(5π/2) = 10 - 10 = 0 τότε Τ = Fελατ = 0
Δ3 β) όταν το σώμα βρεθεί στην κατώτερη θέση της τροχιάς του το ελατήριο θα έχει επιμήκυνση Δl + Α = 0,1 m + 0,1 m = 0,2 m τότε Fελατ = 100 0,2 = 20 Ν τότε Τ = 20 Ν προς τα πάνω
ροπές ως προς Α : Στ(Α) = 0 => Τ (ΑΓ) + FΚ (ΑΚ) - Mg l/2 = 0 => 20 1,2 + FΚ 0,8 - 40 0,6 = 0 =>
=> 24 + 0,8 FΚ - 24 = 0 => FΚ = 0
Δ4. Fελατ = 10 - 10 ημ(10t + 11π/6) = T
ροπές ως προς Κ : Στ(Κ) = 0 => Mg ( l/2 - d ) + T d - FA ( l - d ) = 0 =>
=> 40 ( 0,6 - 0,4 ) + 0,4 [ 10 - 10 ημ(10t + 11π/6) ] - 12 ( 1,2 - 0,4 ) = 0 =>
=> 8 + 4 - 4 ημ(10t + 11π/6) - 9,6 = 0 => ημ(10t + 11π/6) = 2,4 / 4 = 0,6
συν(10t + 11π/6) = [ 1 - 0,62 ]½ = ± 0,8
x = 0,1 ημ(10t + 11π/6) = 0,1 0,6 = 0,06 m υ = 1 συν(10t + 11π/6) = ± 0,8 m/s
a = - 10 ημ(10t + 11π/6) = - 10 0,6 = - 6 m/s2 K = ½ m v2
dK/dt = m v dv/dt = m v a = 1 kg ( ± 0,8 m/s ) (- 6) m/s2 = ± 4,8 J/s
Δ5. επιπλέον ....
Τ(x) = Fελατ(x) = 10 - 100 x - 0,1m £ x £ +0,1m
ροπές ως προς Κ : Στ(Κ) = 0 => Mg ( l/2 - d ) + T d - FA ( l - d ) = 0 =>
=> 40 ( 0,6 - 0,4 ) + 0,4 [ 10 - 100 x ] - FA ( 1,2 - 0,4 ) = 0 =>
=> 8 + 4 - 40 x - FA 0,8 = 0 => FA(x) = 15 - 50 x - 0,1m £ x £ + 0,1m
ροπές ως προς Α : Στ(Α) = 0 => Τ (ΑΓ) + FΚ (ΑΚ) - Mg l/2 = 0 =>
=> 1,2 [ 10 - 100 x ] + FΚ 0,8 - 40 0,6 = 0 =>
=> 12 - 120 x + FΚ 0,8 - 24 = 0 => FK(x) = 15 + 150 x - 0,1m £ x £ + 0,1m
FA + FK + T = 15 - 50 x + 15 + 150 x + 10 - 100 x = 40 = M g
Τ(t) = Fελατ(t) = 10 - 10 ημ(10t + 11π/6)
ροπές ως προς Κ : Στ(Κ) = 0 => Mg ( l/2 - d ) + T d - FA ( l - d ) = 0 =>
=> 40 ( 0,6 - 0,4 ) + 0,4 [ 10 - 10 ημ(10t + 11π/6) - FA ( 1,2 - 0,4 ) = 0 =>
=> 8 + 4 - 4 ημ(10t + 11π/6) - FA 0,8 = 0 => FA(t) = 15 - 5 ημ(10t + 11π/6)
ροπές ως προς Α : Στ(Α) = 0 => Τ (ΑΓ) + FΚ (ΑΚ) - Mg l/2 = 0 =>
=> 1,2 [ 10 - 10 ημ(10t + 11π/6) ] + FΚ 0,8 - 40 0,6 = 0 =>
=> 12 - 12 ημ(10t + 11π/6) ] + FΚ 0,8 - 24 = 0 => FK(t) = 15 + 15 ημ(10t + 11π/6)
FA + FK + T = 15 - 5 ημ(10t + 11π/6) ] + 15 + 15 ημ(10t + 11π/6) + 10 - 10 ημ(10t + 11π/6) = 40 = M g
.............................................................................................................................................................

ΘΈΜΑ Δ.
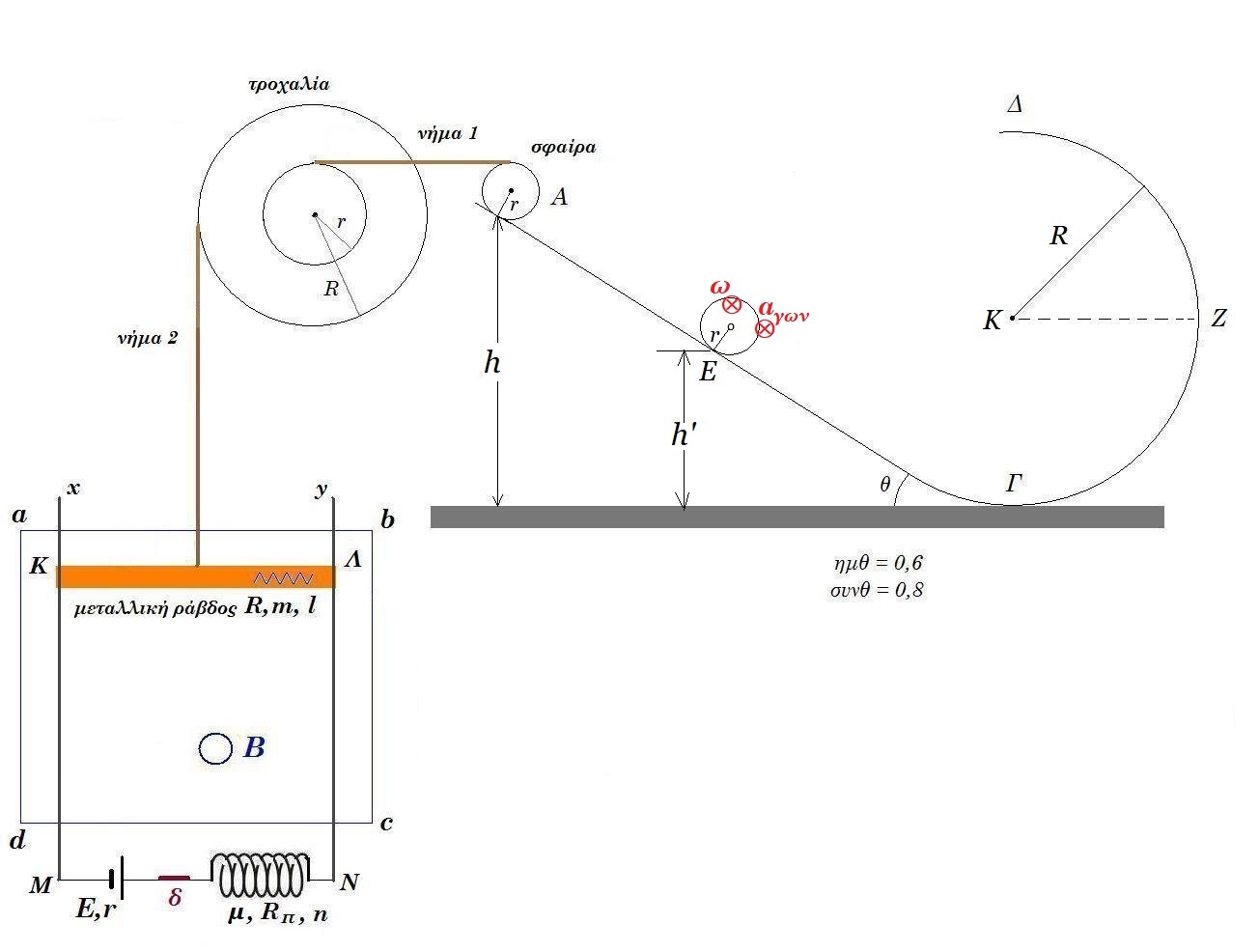
Θεωρούμε την διάταξη του σχήματος, σε κατάσταση ισορροπίας, σε κατακόρυφο επίπεδο. Στη θέση Α του κεκλιμένου επιπέδου ισορροπεί κυκλική στεφάνη μάζας m = 3kg , ακτίνας r = 0,1m. Το κεκλιμένο επίπεδο γωνίας κλίσεως θ, ( ημθ = 0,6 συνθ = 0,8 ) στην βάση του συνδέεται με κατακόρυφο ημικύκλιο ακτίνας R = 1m. Η στεφάνη στο άνω της άκρο συνδέεται με οριζόντιο αβαρές μη εκτατό νήμα 1 (σταθερού μήκους) με τροχαλία μάζας Μ = 5kg εσωτερικής ακτίνας rτροχ = 0,2m , εξωτερικής ακτίνας Rτροχ = 0,5m. Η τροχαλία μπορεί να περιστρέφεται χωρίς τριβές γύρω από άξονα που διέρχεται από το κέντρο της και είναι κάθετος στο επίπεδο της. Γύρω από την τροχαλία έχουμε τυλίξει αρκετές φορές αβαρές μη εκτατό νήμα 2 το οποίο συνδέεται με την μεταλλική ράβδο ΚΛ στο μέσον αυτής. Η μεταλλική ράβδος ισορροπεί σε οριζόντια θέση, έχει μήκος l = 1m και μάζα m=0,5kg, είναι σε επαφή με κατακόρυφους αγωγούς Mx, Ny. Το πηνίο φέρει 1000 σπείρες/m, διαρρέεται από συνεχές ρεύμα εντάσεως Ι, ενώ στο κέντρο του το μέτρο της εντάσεως του μαγνητικού πεδίου είναι Βπην = 4π 10-3 Tesla. Στον χώρο abcd υπάρχει οριζόντιο ομογενές μαγνητικό πεδίο εντάσεως Β.
Δ1. Βρείτε την ένταση του μαγνητικού πεδίου Β φορά, μέτρο.
Κάποια στιγμή ( t0 = 0 ) αφαιρούμε το νήμα 1 και ταυτόχρονα ανοίγουμε τον διακόπτη δ, οπότε η στεφάνη κατέρχεται επί του κεκλιμένου επιπέδου κυλιόμενη ( μη ολισθαίνουσα ) ενώ η ράβδος κινείται κατακόρυφα προς τα κάτω ενώ είναι συνεχώς σε επαφή με τους αγωγούς Mx, Ny και η τροχαλία περιστρέφεται γύρω από τον άξονά της χωρίς τριβές έχοντας γωνιακή επιτάχυνση αγων = 10/3 rad/s2.
Δ2. Εξηγείστε γιατί φορτίζεται η κατερχόμενη ράβδος ΚΛ. Εκφράστε την τάση VΛΚ στα άκρα της, συναρτήσει του χρόνου εάν η ένταση του μαγνητικού πεδίου έχει μέτρο Β = 0,1 Τesla.
Δ3. Τη χρονική στιγμή t0 = 0 η στεφάνη αρχίζει να κατέρχεται κυλιόμενη επί του κεκλιμένου επιπέδου με γωνιακή επιτάχυνση αγων = 30 rad/s2. Τη χρονική στιγμή t1 = 1s φθάνει σε ύψος h' στο σημείο Ε. Βρείτε την ταχύτητα του ανώτερου σημείου της στεφάνης τη χρονική στιγμή t1 καθώς και την επιτάχυνση του σημείου επαφής της στεφάνης με το κεκλιμένο επίπεδο, σημείο Ε.
Δ4. Η στεφάνη κυλίεται (δεν ολισθαίνει) κινούμενη στο κεκλιμένο επίπεδο, διέρχεται από την θέση Γ, ανέρχεται κυλιόμενη στο ημικύκλιο και διέρχεται από την ανώτατη Δ του ημικυκλίου έχοντας ταχύτητα μέτρου υ = 3m/s. Βρείτε την δύναμη που δέχεται από το ημικύκλιο καθώς και την γωνιακή ταχύτητάς της (διεύθυνση, φορά, μέτρο) μετά από 0,2 sec.
Δίνονται : μαγνητική διαπερατότητα του κενού μο = 4π 10-7 Ν/Α2 , επιτάχυνση βαρύτητας g = 10 m/s2
![]() ..................................................................................................................................................................
..................................................................................................................................................................

Βπην = 4π 10-7 i n => 4π 10-3 = 4π 10-7 i 1000 => i = 10 A
FL = B i l => 1 = B 10 1 => B = 0,1 Tesla με φορά προς τα έξω
Δ3. acm = αγων r => acm = 30 rad/s2 0,1 m => acm = 3 m/s2 ω = αγων t = 30 rad/s2 1 s = 30 rad/s
υcm = = ω r = 30 rad/s 0,1 m = 3 m/s
υ2 = υcm2 + (ω r)2 + 2 υcm ω r συνθ = 2 υcm2 (1 + συνθ) = 2 32 (1 + 0,8 ) = 3,6 32 => υ = 3√3,6 m/s2
στο σημείο Ε η στεφάνη έχει τρεις επιταχύνσεις την επιτάχυνση του κέντρου μάζας , την γωνιακή και την κεντρομόλο αλλά η επιτάχυνση του κέντρου μάζας και η γωνιακή είναι αντίθετες και έχουν συνισταμένη μηδέν ενώ η κεντρομόλος ισούται με ακ = υ2 / r = ω2 r = 302 0,1 = 90 m/s2
Δ4. όταν η στεφάνη διέρχεται από την ανώτερη θέση Δ υΔ = 3 m/s :
ΣFy = Fκ => mg + Ν = m vΔ2 / (R - r) => 1 + Ν = 0,1 32 / (1 - 0,1) => Ν = 0,9/0,9 - 1 = 0 άρα μόλις διέρχεται από την ανώτερη θέση Δ του ημικυκλίου διότι ισχύει Ν = 0
η στεφάνη στον αέρα δεν δέχεται δύναμη που να δημιουργεί ροπή συνεπώς η γωνιακή ταχύτητά της είναι σταθερή ω = υΔ / r = 3 m/s / 0,1 m = 30 rad/s
.....................................................................................................................................................................
ΘΕΜΑ Δ
Η διπλή τροχαλία του σχήματος με ακτίνες r1 = 0,05 m και r2 = 2r1, μπορεί να στρέφεται χωρίς τριβές γύρω από οριζόντιο άξονα περιστροφής, που διέρχεται από το κέντρο της. Η τροχαλία έχει αμελητέα μάζα, δηλαδή κάθε στιγμή ισχύει για αυτήν ότι το άθροισμα των ροπών που της ασκούνται ως προς τον άξονα περιστροφής της είναι ίσο με μηδέν, είτε ισορροπεί, είτε περιστρέφεται. Γύρω από το εξωτερικό αυλάκι της τροχαλίας υπάρχει τυλιγμένο ένα αβαρές και μη εκτατό νήμα, στο άκρο του οποίου είναι δεμένο ένα σώμα Σ2 μάζας m2 = 0,5 kg. Στο εσωτερικό αυλάκι της τροχαλίας είναι επίσης τυλιγμένο ένα αβαρές και μη εκτατό νήμα, το άκρο του οποίου είναι δεμένο στο μέσο μιας ομογενούς μεταλλικής ράβδου, ΚΛ, μήκους L = 1 m, αντίστασης R3 και μάζας m1 = 0,2 kg, η οποία μπορεί να κινείται πάνω στους οριζόντιους, αγώγιμους – αμελητέας αντίστασης - οδηγούς Αx και Γx’. Ο συντελεστής οριακής τριβής μεταξύ των οδηγών και της ράβδου ΚΛ έχει τιμή μs = 0,5 και είναι ίσος με το συντελεστή τριβής ολίσθησης (μs=μολ).
Στο χώρο υπάρχει κατακόρυφο ομογενές μαγνητικό πεδίο έντασης μέτρου Β = 2 T με τη φορά των δυναμικών γραμμών προς τα κάτω. Τα σημεία του κυκλώματος Α, Γ συνδέονται μέσω του μεταγωγού δ, είτε με ηλεκτρική πηγή ΗΕΔ Ε = 9 V και εσωτερικής αντίστασης R1 = 1 Ω, είτε με αντίσταση R2 = 1 Ω. Στην αρχή ο μεταγωγός δ βρίσκεται στη θέση Ζ και η ράβδος ισορροπεί με την τριβή να έχει φορά προς τα αριστερά και μέτρο ίσο με το μέτρο της οριακής τριβής.
Δ1. Να υπολογίσετε την αντίσταση R3 της μεταλλικής ράβδου ΚΛ.
Την χρονική στιγμή t=0s φέρνουμε τον μεταγωγό δ στη θέση Ε και η ράβδος αρχίζει να κινείται πάνω στους οδηγούς. Μελετήστε την κίνηση ράβδου και σώματος Σ2
Δ2. Να υπολογίσετε την τάση στα άκρα του αντιστάτη R2 την χρονική στιγμή που το σώμα Σ2 κατέρχεται με επιτάχυνση α2 = 2 m/s2.
Δ3. Να υπολογίσετε την μέγιστη – οριακή – ταχύτητα υορ που θα αποκτήσει το σώμα Σ2.
Δ4. Για το χρονικό διάστημα που απαιτείται για να κάνει η τροχαλία 9 στροφές μετά από την χρονική στιγμή που το σώμα Σ2 αποκτά την μέγιστη – οριακή – ταχύτητα, να υπολογίσετε τη μείωση της δυναμικής ενέργειας του σώματος Σ2 και να επιβεβαιώσετε την ισχύ της αρχής διατήρησης της ενέργειας. Δίνεται g=10 m/s2

Δ1. ο μεταγωγέας δ είναι στη θέση Ζ :
η ράβδος διαρρέεται από ρεύμα i = E / (R1 + R3) (1) και είναι μέσα σε ομογενές μαγνητικό πεδίο Β άρα δέχεται δύναμη Laplace FL = B . i . l (2)
ισορροπία ράβδου ΣF = 0 => Τ1 - FL - Tτρ = 0 => Τ1 - FL - μs . m1 . g = 0 (3)
ισορροπία Σ2 m2 . g = T2 => 0,5 . 10 = T2 => T2 = 5 N (4)
ισορροπία τροχαλίας ( ροπές ) T1 . r1 = T2 . r2 => T1 . r1 = 5 N . 2.r1 => T1 = 10 N (5)
(3), (4), (5) => 10 - FL - 0,5 . 0,2 . 10 = 0 => FL = 9 N (6)
(2), (6) => 9 N = 2 T . i . 1 m => i = 4,5 A
η (1) => R1 + R3 = E / i => R3 = E / i - R1 = 9 / 4,5 - 1 => R3 = 1 Ω
μελέτη της κίνησης ράβδου και σώματος Σ2
σώμα Σ2 : ΣF = m2 α2 => m2 g - Τ2 = m2 α2 => Τ2 = 0,5 10 - 0,5 α2 => Τ2 = 5 - 0,5.α2 (1)
τροχαλία ( ροπές ) T1 . r1 = T2 . r2 => T1 . r1 = Τ2 . 2.r1 => T1 = 2 Τ2 (2)
ράβδος : ΣF = m1 α1 => Τ1 - FL - Tτρ = m1 α1 => Τ1 - Β i l - μs m1 g = m1 α1 =>
=> Τ1 = 2 . i . 1 + 0,5 . 0,2 . 10 + 0,2 . α1 => Τ1 = 2.i + 1 + 0,2 . α1 (3)
νόμος του Ohm : Εεπαγ = i (R2 +R3) => Β υ1 l = i (R2 +R3) => 2 υ1 1 = i (1+1) => υ1 = i
επειδή r2 = 2.r1 τότε υ2 = 2.υ1 => α2 = 2.α1
(3) =>(2),(1) Τ1 = 2.i + 1 + 0,2 . α1 => 2. ( 5 - 0,5.α2 ) = 2.i + 1 + 0,2 . α1 =>
=> 10 - 2α1 = 2.υ1 + 1 + 0,2 . α1 => -2,2.α1 = 2.υ1 - 9 => α1 = -10/11.υ1 + 45/11
η ράβδος κινείται η ταχύτητάς της αυξάνεται οπότε η επιτάχυνσή της ελαττώνεται και κάποια στιγμή θα μηδενισθεί οπότε η ράβδος θα αποκτήσει σταθερή ταχύτητα υορ = 45/11 . 11/10 = 4,5 m/s
μαθηματική ανάλυση :
dv/dt = -10/11 v + 45/11 => dv/dt = -10/11 ( v - 4,5 ) => dv /(v - 4,5) = -10/11 dt =>
=> ln [ (v - 4,5) / (- 4,5) ] = -10/11 t => v - 4,5 = - 4,5 e-10/11 . t =>
=> v(t) = 4,5 ( 1 - e-10/11 . t ) v(0) = 0
a = dv/dt => a(t) = 45/11 e-10/11 . t a(0) = 45/11 m/s2 αρχική επιτάχυνση ράβδου ΚΛ
i(t) = v(t) = 4,5 ( 1 - e-10/11 . t ) i(0) = 0
FL(t) = B l i = 2 1 4,5 ( 1 - e-10/11 . t ) => FL(t) = 9 ( 1 - e-10/11 . t ) FL(0) = 0
Τ2 = 5 - 0,5.α2 = 5 - 0,5 . 2 . 45/11 e-10/11 . t => Τ2 = 5 - 45/11 e-10/11.t
T1 = 2 Τ2 => Τ1 = 2 ( 5 - 45/11 e-10/11 . t ) => Τ1 = 10 - 90/11 e-10/11 t
T1(0) = 10 - 90/11 = 20/11 N
PR = i2 (R3 + R2) = 4,52 ( 1 - e-10/11 . t )2 2 => P(t) = 9 4,5 ( 1 - e-10/11 . t )2
PFL = FL v = 9 ( 1 - e-10/11 . t ) 4,5 ( 1 - e-10/11 . t ) = 9 4,5 ( 1 - e-10/11 . t )2
PTτρ = Ττρ υ = μs m1 g 4,5 ( 1 - e-10/11 . t ) = 0,5 0,2 10 4,5 ( 1 - e-10/11 . t ) =>
=> PTτρ(t) = 4,5 ( 1 - e-10/11 . t )
dK/dt = m1 v a = 0,2 4,5 ( 1 - e-10/11 . t ) 45/11 e-10/11 . t =>
=> dK/dt = 4,5 9/11 e-10/11 . t ( 1 - e-10/11 . t )
PT1 = Τ1 υ = [ 10 - 90/11 e-10/11 . t ] 4,5 ( 1 - e-10/11 . t ) =>
=> ΡΤ1 = 45 [ 1 - 9/11 e-10/11 . t ] ( 1 - e-10/11 . t )
η ράβδος ΚΛ κινείται λόγω της τάσης νήματος Τ1 , που έχει διπλάσιο μέτρο από την τάση νήματος Τ2 η οποία ασκείται στο σώμα Σ2 , υπάρχει δύναμη τριβής , δύναμη Laplace οι οποίες είναι αντίρροπες της Τ1 και η ράβδος έχει ταχύτητα
PFL + PTτρ + dK/dt =
= 9 4,5 ( 1 - e-10/11 . t )2 + 4,5 ( 1 - e-10/11 . t ) + 4,5 9/11 e-10/11 . t ( 1 - e-10/11 . t ) =
= 4,5 ( 1 - e-10/11 . t ) [ 9 ( 1 - e-10/11 . t ) + 1 + 9/11 e-10/11 . t ] =
= 4,5 ( 1 - e-10/11 . t ) [ 10 - 9 e-10/11 . t + 9/11 e-10/11 . t ] =
= 4,5 ( 1 - e-10/11 . t ) [ 10 - 90/11 e-10/11 . t ] = PT1
Δ2. ο μεταγωγέας δ είναι στη θέση Ε :
ΣF = m2 α2 => m2 g - Τ2 = m2 α2 => 0,5 10 - Τ2 = 0,5 2 => Τ2 = 4 Ν
T1 . r1 = T2 . r2 => T1 . r1 = 4 N . 2.r1 => T1 = 8 N
η ράβδος κινείται μέσα σε μαγνητικό πεδίο κάθετα στις δυναμικές γραμμές, στα ηλεκτρόνια της ράβδου ασκούνται δυνάμεις Lorenz με συνέπεια να μετακινούνται προς το άκρο Κ το οποίο φορτίζεται αρνητικά (-) οπότε το άκρο Λ φορτίζεται θετικά (+), έτσι η ράβδος γίνεται πηγή ηλεκτρικού ρεύματος, στα άκρα ΚΛ εμφανίζεται επαγωγική τάση Εεπαγ = Β . υ1 . l
νόμος του Ohm για κλειστό κύκλωμα : Εεπαγ = i (R2 +R3) => Β υ1 l = i (R2 +R3)
η τροχαλία περιστρέφεται με γωνιακή ταχύτητα ω = αγων .t τότε υ1 = ω . r1 & υ2 = ω . r2 επειδή r2 = 2.r1 τότε υ2 = 2.υ1 => α2 = 2.α1 ( επιταχύνσεις ) άρα α1 = 1 m/s2
η ράβδος δέχεται δύναμη Laplace FL = B . i . l & τάση νήματος Τ1 = 8 Ν
δύναμη τριβής : ΣF = Τ1 - FL - Tτρ = m1 α1 => 8 - FL - 0,5 0,2 10 = 0,2 1 => FL = 6,8 Ν
από τη σχέση FL = B i l => 6,8 Ν = 2 Τ i 1 m => i = 3,4 A
η τάση στα άκρα της R2 : V2 = VΓΕ = 3,4 Α 1 Ω => VΓΕ = 3,4 Volt
από τη σχέση Β υ1 l = i (R2 +R3) => υ1 = 3,4 (1 + 1) / 2.1 => υ1 = 3,4 m/s
Δ3. σώμα Σ2 : ΣF = 0 => Τ2 - m2 g = 0 => Τ2 = 5 Ν
τροχαλία ( ροπές ) T1 . r1 = T2 . r2 => T1 r1 = 5 N 2.r1 => T1 = 10 N
ράβδος : ΣF = 0 => Τ1 - FL - Tτρ = 0 => Τ1 - Β i l - μs m1 g = 0 => 10 - 2 i 1 - 0,5 0,2 10 = 0 =>
=> i = 4,5 A
νόμος Ohm : Εεπαγ = i (R2 +R3) => Β υορ l = i (R2 +R3) => 2 υορ 1 = 4,5 .(1+1) => υορ = 4,5 m/s
επειδή r2 = 2.r1 τότε υ2 = 2.υορ = 9 m/s το Σ2 θα κινείται με οριακή ταχύτητα υορ(2) = 9 m/s
Δ4. η τροχαλία κάνει Ν = 9 περιστροφές τότε θ = Ν 2π rad = 18π rad
υορ(2) = ω r2 => ω = 9 m/s / 0,1 m => ω = 90 rad/s ω = θ / t => t = 18π / 90 => t = 0,2.π s
η ράβδος διανύει διάστημα x1 = υορ t = 4,5 m/s 0,2.π s => x1 = 0,9.π m
το σώμα Σ2 διανύει διάστημα x2 = υορ(2) t = 9 m/s 0,2.π s => x2 = 1,8.π m = h
U(Σ2) = m2 g h = 0,5 kg 10 m/s2 1,8.π m => U(Σ2) = 9.π Joule = T2 x2 = WT2
WT1 = T1 x1 = 10 N 0,9.π m => WT1 = 9.π Joule
WTτρ = Tτρ x1 = μs m1 g x1 = 0,5 0,2 10 0,9.π => WTτρ = 0,9.π Joule
FL = B i l = 2 Τ 4,5 Α 1 m = 9 N WFL = FL x1 = 9 N 0,9.π m => WFL = 8,1.π Joule
Qθερμ = i2 (R2 + R3) t => Qθερμ = 4,52 (1 + 1) 0,2.π => Qθερμ = 8,1.π Joule
παρατηρούμε ότι καθώς κατεβαίνει το σώμα Σ2 η δυναμική βαρυτική ενέργεια μειώνεται κατά 9π J η ράβδος κερδίζει ενέργεια 9.π J λόγω το έργου που παράγει η τάση του νήματος η οποία ενέργεια καταναλώνεται στις τριβές 0,9.π J και στην δύναμη Laplace 8,1.π J η οποία ισούται με την θερμότητα λόγω φαινομένου Joule πάνω στις αντιστάσεις R2 και R3
ΘΕΜΑ Δ
Η διπλή τροχαλία του σχήματος με ακτίνες r1 = 0,05 m και r2 = 2r1, μπορεί να στρέφεται χωρίς τριβές γύρω από οριζόντιο άξονα περιστροφής, που διέρχεται από το κέντρο της. Η τροχαλία έχει αμελητέα μάζα, δηλαδή κάθε στιγμή ισχύει για αυτήν ότι το άθροισμα των ροπών που της ασκούνται ως προς τον άξονα περιστροφής της είναι ίσο με μηδέν, είτε ισορροπεί, είτε περιστρέφεται. Γύρω από το εξωτερικό αυλάκι της τροχαλίας υπάρχει τυλιγμένο ένα αβαρές και μη εκτατό νήμα, στο άκρο του οποίου είναι δεμένη στο μέσο ομογενής μεταλλική ράβδος ΜΝ, μήκους L2 = 2 m, αντίστασης RΜΝ = 1,01 Ω και μάζας m2 = 0,5 kg, η οποία μπορεί να κινείται χωρίς τριβές πάνω στους κατακόρυφους, αγώγιμους – αμελητέας αντίστασης - οδηγούς Σy και Τy'. Τα άκρα των οδηγών Σ, Τ συνδέονται με καλώδια αμελητέας αντίστασης με αμπερόμετρο αντίστασης RΑ = 1 Ω και βολτόμετρο αντίστασης RV = 99 Ω, όπως στο σχήμα. Στο εσωτερικό αυλάκι της τροχαλίας είναι επίσης τυλιγμένο ένα αβαρές και μη εκτατό νήμα, το άκρο του οποίου είναι δεμένο στο μέσο μιας ομογενούς μεταλλικής ράβδου, ΚΛ, μήκους L1 = 1 m, αντίστασης RΚΛ και μάζας m1 = 0,2 kg, η οποία μπορεί να κινείται πάνω στους οριζόντιους, αγώγιμους – αμελητέας αντίστασης - οδηγούς Αx και Γx’. Ο συντελεστής οριακής τριβής μεταξύ των οδηγών και της ράβδου ΚΛ έχει τιμή μs = 0,5 και είναι ίσος με το συντελεστή τριβής ολίσθησης (μs=μολ).
Στον χώρο υπάρχει ομογενές μαγνητικό πεδίο έντασης μέτρου Β = 0,5 T που σχηματίζει με την οριζόντιο γωνία φ με ημφ = 0,6 και συνφ = 0,8 όπως στο σχήμα. Τα σημεία του κυκλώματος Α, Γ συνδέονται μέσω του μεταγωγού δ, είτε με ηλεκτρική πηγή ηλεκτρεγερτικής δύναμης Ε = 9 V και εσωτερικής αντίστασης r = 0,1 Ω, είτε με αντίσταση R = 0,8 Ω. Στην αρχή ο μεταγωγός δ βρίσκεται στη θέση Ζ και η ράβδος ισορροπεί με την τριβή να έχει φορά προς τα αριστερά και μέτρο ίσο με το μέτρο της οριακής τριβής.
Δ1. Να υπολογίσετε την αντίσταση RΚΛ της μεταλλικής ράβδου ΚΛ.
Την χρονική στιγμή t=0s φέρνουμε τον μεταγωγό δ στη θέση Δ και η ράβδος ΚΛ αρχίζει να κινείται πάνω στους οδηγούς Αx Γx'.
Δ2. Μελετήστε την κίνηση των ράβδων ΚΛ και ΜΝ. Βρείτε τις ενδείξεις των οργάνων αμπερομέτρου και βολτομέτρου συναρτήσει του χρόνου.

Δ1. ο μεταγωγέας δ είναι στη θέση Ζ :
η ράβδος ΚΛ διαρρέεται από ρεύμα i = E / (r + RΚΛ) (1) και είναι μέσα σε ομογενές μαγνητικό πεδίο Β άρα δέχεται δύναμη Laplace FL = B ημφ i l (2)
ισορροπία ράβδου ΚΛ : ΣF = 0 => Τ1 - FL - Tτρ = 0 => Τ1 - FL - μs m1 g = 0 (3)
ισορροπία ράβδου ΜΝ : m2 g = T2 => 0,5 10 = T2 => T2 = 5 N (4)
ισορροπία τροχαλίας ( ροπές ) : T1 . r1 = T2 . r2 => T1 r1 = 5 N 2.r1 => T1 = 10 N (5)
(3), (4), (5) => 10 - FL - 0,5 . 0,2 . 10 = 0 => FL = 9 N (6)
(2), (6) => 9 N = 0,5.0,6 T . i . 1 m => i = 9/0,3 = 30 A
η (1) => r + RΚΛ = E / i => RΚΛ = E / i - r = 9/30 - 0,1 => RΚΛ = 0,2 Ω
ο μεταγωγέας δ είναι στη θέση Δ :
μελέτη της κίνησης ράβδου και σώματος Σ2
ράβδος ΜΝ : ΣF = m2 . α2 => m2 . g - FL2 - Τ2 = m2 . α2 =>
=> m2 g - Β συνφ i2 lΜΝ - Τ2 = m2 α2 => 0,5 10 - 0,5 0,8 i2 2 - Τ2 = 0,5 α2 =>
=> 5 - 0,8 . i2 - 0,5 . α2 = Τ2 (1)
νόμος του Ohm : Εεπαγ = i2 (RMN + RA,V) => Β συνφ υ2 lΜΝ = i2 (1,01 + 1 99/100) =>
=> 0,5 0,8 υ2 2 = i2 2 => 0,4 υ2 = i2
(1) => Τ2 = 5 - 0,8 0,4 υ2 - 0,5 α2 = 5 - 0,32 υ2 - 0,5 α2
τροχαλία ( ροπές ) T1 . r1 = T2 . r2 => T1 . r1 = Τ2 . 2.r1 => T1 = 2 Τ2 (2)
ράβδος ΚΛ : ΣF = m1 α1 => Τ1 - FL1 - Tτρ = m1 α1 => Τ1 - Β ημφ i1 lΚΛ - μs m1 g = m1 α1 =>
=> Τ1 = 0,5.0,6 i1 1 + 0,5 0,2 10 + 0,2 α1 => Τ1 = 0,3.i1 + 1 + 0,2 α1 (3)
νόμος του Ohm : Εεπαγ = i1 . (R + RΚΛ) => Β ημφ . υ1 . l = i1 . (R + RΚΛ) =>
=> 0,3 . υ1 . 1 = i1 . (0,8 + 0,2) => 0,3 υ1 = i1
(3) => Τ1 = 0,3. 0,3.υ1 + 1 + 0,2 . α1 = 0,09.υ1 + 1 + 0,2 . α1
επειδή r2 = 2.r1 τότε υ2 = 2.υ1 => α2 = 2.α1
(3) =>(2),(1) T1 = 2 Τ2 => 0,09.υ1 + 1 + 0,2 . α1 = 2 { 5 - 0,32 . υ2 - 0,5 . α2 } =>
=> 0,09.υ1 + 1 + 0,2 . α1 = 2 { 5 - 0,32 . 2.υ1 - 0,5 . 2.α1 } =>
=> 0,09.υ1 + 1 + 0,2 . α1 = 10 - 1,28.υ1 - 2.α1 =>
=> 2,2 . α1 = 9 - 1,37.υ1 => α1 = 45/11 - 137/220 υ1
η ράβδος ΚΛ κινείται η ταχύτητάς της αυξάνεται οπότε η επιτάχυνσή της ελαττώνεται και κάποια στιγμή θα μηδενισθεί οπότε η ράβδος ΚΛ θα αποκτήσει σταθερή ταχύτητα υορ,1 = 900/137 m/s = 6,57 m/s
μαθηματική ανάλυση :
dv/dt = - 137/220 v + 45/11 => dv/dt = - 137/220 ( v - 6,57 ) => dv / (v - 6,57) = - 137/220 dt =>
=> ln [ (v - 6,57) / (- 6,57) ] = - 137/220 t => v - 6,57 = - 6,57 e- 137/220 . t =>
v1 (t) = 900/137 ( 1 - e- 137/220 . t ) ταχύτητα ράβδου ΚΛ v1(0) = 0 αρχική ταχύτητα
a = dv/dt => a1 (t) = 900/137 . 137/220 e- 137/220 . t = 45/11 e- 137/220 . t επιτάχυνση ράβδου ΚΛ
a(0) = 45/11 m/s2 αρχική επιτάχυνση ράβδου ΚΛ
i1 (t) = 0,3 v1 (t) = 0,3 . 900/137 ( 1 - e- 137/220 . t ) = 270/137 ( 1 - e- 137/220 . t ) i1 (0) = 0
FL1(t) = B l i1 = 0,3 1 270/137 ( 1 - e- 137/220 . t ) => FL(t) = 81/137 ( 1 - e- 137/220 . t ) FL1(0) = 0
v2 (t) = 2 υ1 = 1800/137 ( 1 - e- 137/220 . t ) ταχύτητα ράβδου ΜΝ
a = dv/dt => a2 (t) = 2 α1 = 90/11 e- 137/220 . t επιτάχυνση ράβδου ΜΝ
i2 = 0,4 v2 = 720/137 ( 1 - e- 137/220 . t ) ρεύμα που διαρρέει την ράβδο ΜΝ
Τ (+) Σ (-) , M (+) N (-)
Vπολική = VMN = iV RV = iA RA = E - i2 RMN = B συνφ v2 lMN - i2 RMN
iV RV = iA RA => iV 99 = iA 1 => 99 iV = iA
i2 = iA + iV = 100 iV
B συνφ v2 lMN - i2 RMN = iV RV => 0,5 0,8 v2 2 - 100 iV 1,01 = iV 99 => 0,8 v2 = 200 iV
iA = 99 0,4 v2 / 100 = 0,396 v2 ένδειξη αμπερομέτρου
VMN = iV RV = 0,004 v2 99 = 0,396 v2 = VV ένδειξη βολτομέτρου
όπου v2 = 1800/137 ( 1 - e- 137/220 . t )
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
ΘΈΜΑ Δ.
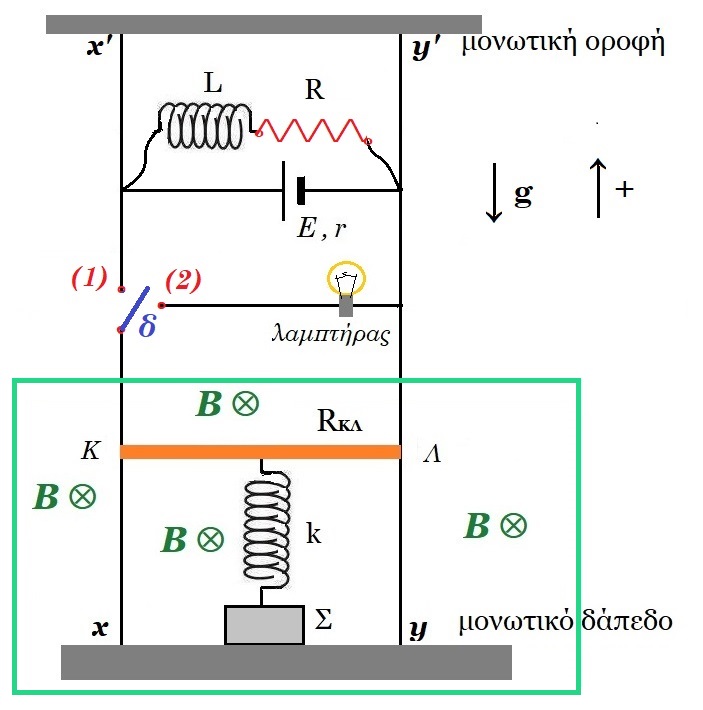 |
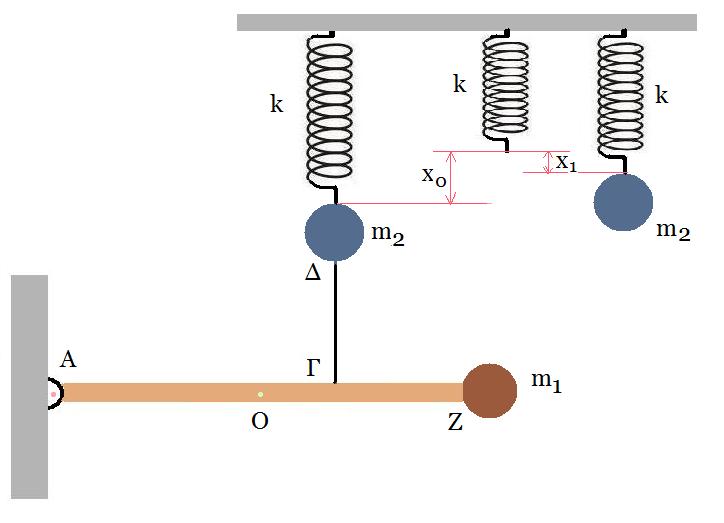
L = 0,1 H , N/l = 100 σπείρες/m , Rπην.= 0 , Ε = 24 V, r = 1 Ω, R = 10 Ω, RΚΛ = 10 Ω, lΚΛ = 1 m, m = 1 kg, MΣ = 2 kg, k = 100 N/m, Β = 0,5 T, λαμπτήρας Rλ = 10 Ω Α) Ο διακόπτης δ είναι στη θέση (1), η διάταξη βρίσκεται σε ισορροπία, βρείτε την ένταση του μαγνητικού πεδίου στο κέντρο του πηνίου. Β) Ανοίγουμε τον διακόπτη δ, Β1) βρείτε την δύναμη που δέχεται το σώμα Σ από το μονωτικό δάπεδο συναρτήσει του χρόνου. Χάνει την επαφή του το σώμα με το δάπεδο; Β2) μελέτη της κίνησης της αγώγιμης ράβδου ΚΛ μέσα στο μαγνητικό πεδίο. Γ) Μετακινούμε τον διακόπτη δ από την θέση (1) στην (2), Γ1) μελέτη της κίνησης της αγώγιμης ράβδου ΚΛ μέσα στο μαγνητικό πεδίο Γ2) πως μεταβάλλεται η ένταση του ρεύματος που διαρρέει το πηνίο; υπολογίστε τον ρυθμό μεταβολής της δυναμικής ενέργειας του πηνίου αμέσως μόλις ο διακόπτης φύγει από τη θέση (1) και μετά από πολύ χρόνο εκφράστε την ένταση του ρεύματος που διαρρέει το πηνίο συναρτήσει του χρόνου. |
Α) ο διακόπτης δ είναι κλειστός και η διάταξη είναι σε ισορροπία :
Ε = i [ r + R .RΚΛ / (R + RΚΛ) ] => 24 = i [ 1 + 10.10/(10+10) ] => 24 = i ( 1 + 5 ) => i = 4 A
η αντίσταση R διαρρέεται από ρεύμα εντάσεως iR = 2Α η ράβδος ΚΛ διαρρέεται από ρεύμα εντάσεως iΚΛ = 2Α
ισορροπία ράβδου : ΣFy = 0 => FL - mg + Fελατ. = 0 =>
=> B l iΚΛ - mg + k Δl = 0 => 0,5 1 2 - 1 10 + 100 Δl = 0 => Δl = 0,09 m συσπείρωση ελατηρίου
το πηνίο διαρρέεται από ρεύμα εντάσεως iR = 2 Α στο κέντρο του η ένταση του μαγνητικού πεδίου είναι :
Βπην. = 4π 10-7 Ν/l iR = 4π 10-7 100 2 => Βπην = 8π 10-5 T
Β) ανοίγουμε τον διακόπτη δ :
ισορροπία ράβδου : Fελατ. - mg = 0 => k Δl = mg => 100 Δl = 10 => Δl = 0,1 m συσπείρωση ελατηρίου
k = m ω2 => ω2 = 100 => ω = 10 rad/s T = 2π/ω = π/5 s A = 0,1 - 0,09 = 0,01 m
y(t) = 0,01 ημ(10t + π/2) υ(t) = 0,1 συν(10t + π/2) α(t) = - 1 ημ(10t + π/2)
ΣFy = m a => - mg + Fελατ. = m a => - 10 + Fελατ. = 1 [ - 1 ημ(10t + π/2) ] =>
=> Fελατ.(t) = 10 - ημ(10t + π/2) Fελατ.(0) = 10 - ημ(π/2) = 9 N
Fελατ.(T/4) = 10 - ημ(10 π/20 + π/2) = 10 - 0 = 10 N
Fελατ.(T/2) = 10 - ημ(10 π/10 + π/2) = 10 + 1 = 11 N
Fελατ.(3T/4) = 10 - ημ(10 3π/20 + π/2) = 10 - 0 = 10 N
Β1) το σώμα Σ δέχεται δύναμη από το ελατήριο : F'ελατ.(t) = - Fελατ.(t) = - 10 + 1 ημ(10t + π/2)
ΣFy = 0 => - ΜΣ g + F'ελατ. + Ν = 0 => - 20 - 10 + ημ(10t + π/2) + Ν = 0 =>
=> Ν(t) = 30 - ημ(10t + π/2) αντίδραση από το μονωτικό δάπεδο πάνω στο σώμα Σ
το σώμαα Σ ΔΕΝ χάνει την επαφή του με το μονωτικό δάπεδο 29 Ν £ Ν(t) £ 31 Ν
Β2) η αγώγιμη ράβδος ΚΛ κινείται μέσα στο μαγνητικό πεδίο εντάσεως Β = 0,5 Τ κάθετα στις δυναμικές γραμμές του πεδίου, οπότε τα ηλεκτρόνιά της δέχονται δύναμη Lorentz με συνέπεια να μετακινούνται προς το ένα άκρο το οποίο φορτίζεται αρνητικά ενώ το άλλο άκρο φορτίζεται θετικά έτσι εμφανίζεται επαγωγική τάση :
Εεπαγ = Β l υ = 0,5 1 0,1 συν(10t + π/2) => Εεπαγ(t) = 0,05 συν(10t + π/2)
Γ1) κλείνει κύκλωμα με τον λαμπτήρα και την ράβδο η οποία όπως κινείται έχει στα άκρα της τάση άρα διαρρέεται από ρεύμα εντάσεως i = Εεπαγ / ( RΚΛ + Rλ ) = Β l υ / ( RΚΛ + Rλ ) = 0,5 1 υ / (10 + 10) => i = υ / 40 και επειδή κινείται μέσα σε μαγνητικό πεδίο κάθετα στις δυναμικές γραμμές του, δέχεται δύναμη Laplace αντίρροπη της ταχύτητάς του και έχει μέτρο : FL = B l i = 0,5 1 υ / 40 = υ / 80 της μορφής : F = - b v , b = 1/80 kg/s
ο αγωγός θα εκτελέσει φθίνουσα Α.Α.Τ. με αρχικό πλάτος Α0 = 0,01 m
το πλάτος της ταλάντωσης μεταβάλλεται με τον χρόνο σύμφωνα με την σχέση : Α = Α0 e-Λt
όπου Λ = b/2m = 1/80 / 2 .1 = 1/160 s-1 τελικά : Α(t) = 0,01m e-t/160
y(t) = 0,01 e-t/160 ημ(10t + π/2)
υ = dy/dt = - 0,01/160 e-t/160 ημ(10t + π/2) + 0,01 e-t/160 10 συν(10t + π/2) =>
=> υ(t) = [ - 1/16000 ημ(10t + π/2) + 0,1 συν(10t + π/2) ] e-t/160
α = dv/dt =
= [- 1/1600 συν(10t + π/2) - ημ(10t + π/2) + 1/2560000 ημ(10t + π/2) - 1/1600 συν(10t + π/2) ] e-t/160 =>
=> α(t) = [- 1/800 συν(10t + π/2) - ημ(10t + π/2) + 1/2560000 ημ(10t + π/2) ] e-t/160
ΣF = m a => - mg + Fελατ + FL = ma => - mg + Fελατ - υ / 80 = ma
Γ2) κλείνει κύκλωμα με την πηγή συνεχούς ρεύματος,το πηνίο και την αντίσταση R : E - L di/dt = i (r + R)
αρχικά i = 2 A οπότε E - L di/dt = i (r + R) => 24 - 0,1 di/dt = 2 (1 + 10) => di/dt = 20 A/s
μετά από πολύ χρόνο i = E / (r + R) = 24 / 11 A
οπότε E - L di/dt = i ( r + R ) => 24 - 0,1 di/dt = 24/11 11 => di/dt = 0
U = ½ L i2
αρχικά dU/dt = L i di/dt = 0,1 H 2 A 20 A/s = 4 J/s
μετά από πολύ χρόνο dU/dt = L i di/dt = 0,1 H 2 A 0 A/s = 0 J/s
μαθηματική ανάλυση :
E - L di/dt = i ( r + R ) => - L di/dt = i ( r + R ) - E =>
=> - L di/dt = (r + R) [ i - E/(r + R) ] => di / [ i - E/(r + R) ] = - (r + R)/L dt =>
=> ln { [ i - E/( r + R ) ] / [ I0 - E/( r + R ) ] } = - ( r + R )/L . t =>
=> i = E/(r + R) + [ I0 - E/(r + R) ] e- (r + R)/L.t => i(t) = 24/11 + (2 - 24/11) . e- 110.t
i(0) = 24/11 + ( 2 - 24/11 ) e0 = 2 A t ® ¥ i ® 24/11 Α
di/dt = [ I0 - E/( r + R ) ] [ - ( r + R ) / L ] . e- ( r + R )/L . t =>
=> di/dt = [ E - I0 ( r + R ) ] / L . e- ( r + R )/L . t
di/dt = [ 24 - 2 . 11 ] / 0,1 . e- 110 . t = 20 . e- 110 . t
t = 0 di/dt = 20 A/s t ® ¥ di/dt ® 0
U = ½ L i2
dU/dt = L i didt = 0,1 [ 24/11 . ( 1 - e- 110 . t ) + 2 . e- 110 . t ] 20 . e- 110 . t
t = 0 dU/dt = 0,1 2 20 = 4 J/s t ® ¥ dU/dt ® 0
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~

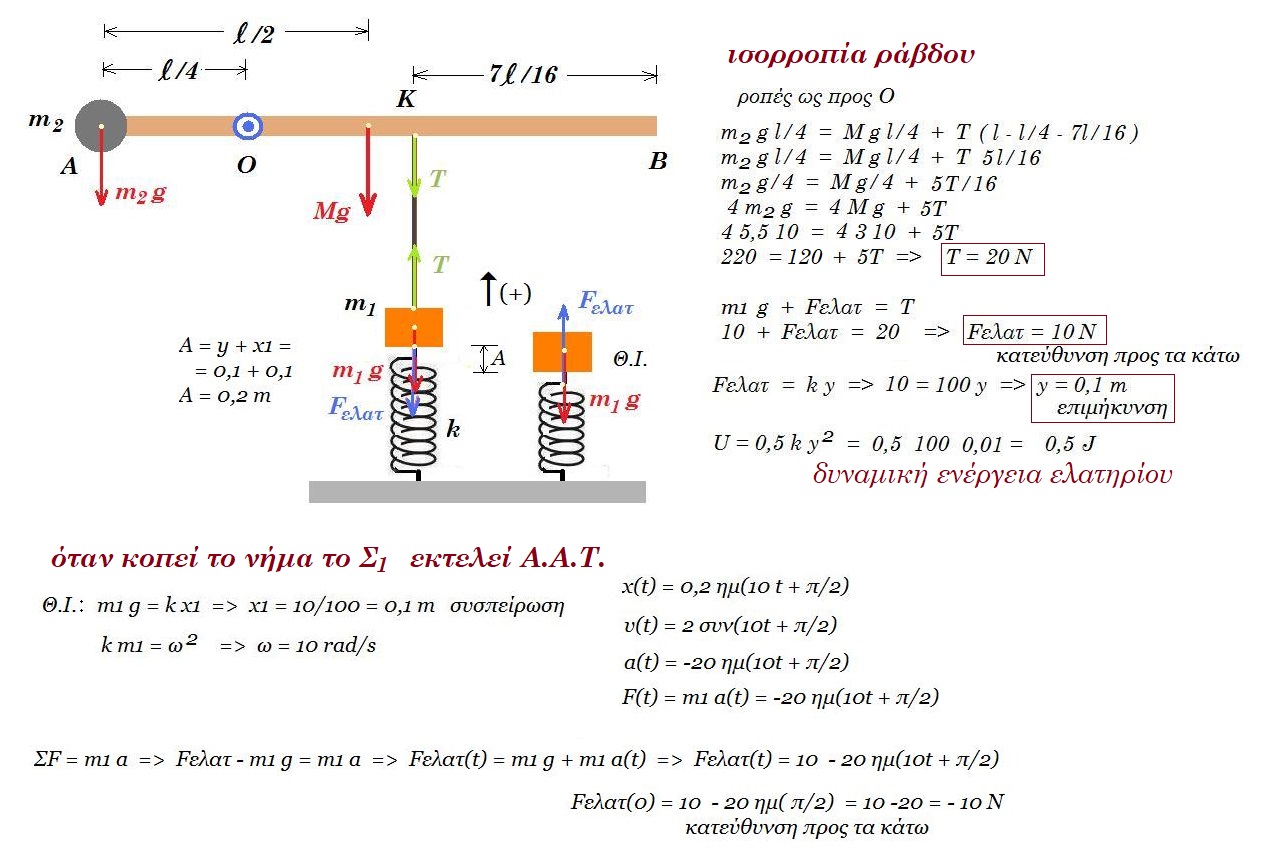

Ομογενής άκαμπτη ράβδος ΑΖ άχει μήκος L = 4 m, μάζα M = 3 kg, ισορροπεί σε οριζόντια θέση. Στο άκρο Α υπάρχει ακλόνητη άρθρωση γύρω από την οποία η ράβδος μπορεί να περιστρέφεται, χωρίς τριβές ενώ στο άλλο άκρο Ζ υπάρχει στερεωμένο σφαιρίδιο μάζας m1 = 1 kg και αμελητέων διαστάσεων. Ένα αβαρές τεντωμένο νήμα ΔΓ συνδέει το σημείο Γ της ράβδου με σφαιρίδιο μάζας m2 = 1 kg, το οποίο είναι στερεωμένο στο ελεύθερο άκρο ιδανικού ελατηρίου σταθεράς k = 100 N/m. Το άλλο άκρο του ελατηρίου είναι ακλόνητο. Η απόσταση ΑΓ είναι ίση με 2,5 m. Όλη η διάταξη βρίσκεται στο ίδιο κατακόρυφο επίπεδο, στο οποίο γίνονται όλες οι κινήσεις.
(Α) Να υπολογίσετε την δυναμική ενέργεια του ελατηρίου.
Αν κόψουμε το νήμα ΔΓ το σφαιρίδιο m2 εκτελεί αμείωτη αρμονική ταλάντωση, ενώ η ράβδος μαζί με το σώμα m1 υπό την επίδραση της βαρύτητας, περιστρέφονται χωρίς τριβές γύρω από το Α.
(Β) Να υπολογίσετε το χρόνο που χρειάζεται το σφαιρίδιο m2 από τη στιγμή που κόβεται το νήμα μέχρι τη στιγμή που θα φθάσει στην υψηλότερη θέση του για πρώτη φορά.
(Γ) Να εκφράσετε την δύναμη ελατηρίου συναρτήσει του χρόνου και την δυναμική ενέργεια του ελατηρίου συναρτήσει της απομάκρυνσης x από τη θέση ισορροπίας του σφαιριδίου m2.
(Δ) Υπολογίστε την κινητική ενέργεια του συστήματος ράβδου - σφαιριδίου m1, τη στιγμή που η ράβδος περνά από την κατακόρυφη θέση.
(Ε) Υπολογίστε την γραμμική ταχύτητα του Σ1 τη στιγμή που η ράβδος περνά από την κατακόρυφη θέση, αν η γωνιακή ταχύτητα του συστήματος ράβδου - σφαιριδίου m1 είναι ω = 2,5 r/s.
κέντρο μάζας : ( θεωρώ ως προς το Α ) (M + m1) xcm = M L/2 + m1 L =>
=> (3 + 1) xcm = 3 2 + 1 4 => xcm = 10/4 = 2,5 m ως προς το Α
A. ροπές ως προς Α : Μ g L/2 + m1 g L = T (ΑΓ) => 3 10 4/2 + 110 4 = T 2,5 => Τ = 40 Ν
ισορροπία m2 : m2 g + T - Fελατ = 0 => 1 10 + 40 - k x0 = 0 => x0 = 50/100 = 0,5 m αρχική επιμήκυνση ελατηρίου
δυναμική ενέργεια ελατηρίου : Uελατ = ½ k x02 = ½ 100 0,52 = 12,5 Joule
Fελατ = k x0 = 100 0,5 = 50 Ν
Β. το σύστημα ελατήριο - Σ2 ισορροπεί : m2 g = Fελατ => 1 10 = k x1 => x1 = 10/100 = 0,1m άρα το πλάτος ταλάντωσης θα είναι : Α = 0,5m - 0,1m = 0,4m
το σώμα m2 εκτελεί ΑΑΤ με κυκλική συχνότητα ω2 = k/m1 = 100/1 => ω = 10 rad/s
T = 2π/ω = 2π/10 = π/5 sec
στην ισορροπία το σώμα βρίσκεται στην κάτω άκραία θέση της ταλάντωσης
θα πάει για πρώτη φορά στην άνω ακραία θέση εντός χρόνου t = T/2 = π/10 sec
Γ. η εξίσωση της απομάκρυνσης συναρτήσει του χρόνου είναι :
x(t) = A ημ(ωt + θ) => x(t) = 0,4 ημ(10t + π/2) = 0,4 συν10t ( θετική φορά προς τα κάτω )
ταχύτητα : υ(t) = 4 συν(10t + π/2) = - 4 ημ10t
επιτάχυνση : α(t) = - 40 ημ(10t + π/2) = - 40 συν10t
δύναμη επαναφοράς : F(t) = m2 a(t) = - 40 συν10t
δύναμη ελατηρίου : Fελατ(t) = k { x1 + x(t) } = 100 { 0,1 + 0,4 συν10t } = 10 + 40 συν10t
Fελατ(0) = 10 + 40 συν0 = 10 + 40 = +50 Ν
στην ισορροπία του m2 με το νήμα, το ελατήριο είναι επιμηκυμένο κατά 0,5 m οπότε η δύναμη ελατηρίου είναι Fελατ(0) = k x0 = 100 N/m 0,5 m = +50 N
Uελατ = ½ k ( x1 + x )2 = ½ 100 ( 0,1 + x )2 = 50 ( 0,1 + x )2 - 0,4 m £ x £ + 0,4 m θετική φορά προς τα κάτω
στις ακραίες θέσεις :
x = - 0,4 m Uελατ = ½ 100 ( 0,1 + (- 0,4) )2 = 4,5 J Fελατ = 100 (0,1 - 0,4) = - 30 Ν
x = + 0,4 m Uελατ = ½ 100 ( 0,1 + 0,4 )2 = 12,5 J Fελατ = 100 (0,1 + 0,4) = +50 Ν
στη θέση ισορροπίας : x = 0 Uελατ = ½ 100 0,12 = 0,5 J Fελατ = 100 0,1 = +10 Ν
Δ. διατήρηση ενέργειας : Uαρχ = Kτελ => Μ g L/2 + m1 g L = Κ =>
=> Κ = 3 10 4/2 + 1 10 4 = 60 + 40 => Κ = 100 J
Ε. το σύστημα ράβδος - σφαιρίδιο m1 έχει γωνιακή ταχύτητα ω = 2,5 rad/s τη στιγμή που η ράβδος περνά από την κατακόρυφη θέση
διατήρηση ενέργειας : Μ g L/2 + m1 g L = ½ 1/3 Μ L2 ω2 + ½ m1 υ2 =>
=> Μ g L/2 + m1 g L = ½ 1/3 Μ L2 ω2 + ½ m1 υ2 =>
=> 30 2 + 10 4 = ½ 1/3 3 42 ω2 + ½ 1 42 ω2 =>
=> 60 + 40 = 16 ω2 => ω2 = 100/16 = 6,25 => ω = 2,5 rad/s
η γραμμική ταχύτητα του Σ1 είναι : υm1 = ω L = 2,5 rad/s 4 m = 10 m/s
η γραμμική ταχύτητα του κέντρου μάζας του συστήματος ράβδος - σφαιρίδιο m1 είναι :
υcm = ω xcm = 2,5 rad/s 2,5 m = 6,25 m/s
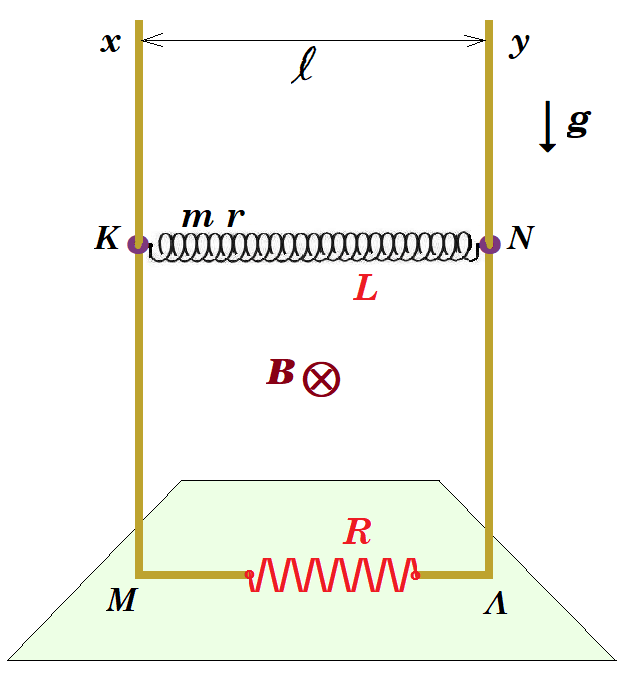
ΘΕΜΑ Δ

Σημειακό σώμα Σ μάζας m = 1 kg ισορροπεί ακίνητο δεμένο στο κάτω άκρο ιδανικού κατακόρυφου ελατηρίου σταθεράς k = 100 N/m το πάνω άκρο του οποίου είναι στερεωμένο σε σημείο της οροφής. Σε κατακόρυφη απόσταση d = 0,3 m κάτω από το σώμα Σ βρίσκεται το άκρο Α λείας, οριζόντιας, ομογενούς ράβδου (ΑΓ) μάζας Μ = 4kg και μήκους L = 1 m που ισορροπεί ακίνητη ενώ βρίσκεται σε επαφή με δυο υποστηρίγματα Υ1 και Υ2 που ισαπέχουν από το κέντρο μάζας της απόσταση d1 = d2 = 0,4 m. Μετατοπίζουμε το σώμα Σ κατακόρυφα προς τα πάνω κατά 0,5 m και την χρονική στιγμή t0 = 0 το αφήνουμε ελεύθερο χωρίς αρχική ταχύτητα με αποτέλεσμα να ξεκινήσει απλή αρμονική ταλάντωση. Την χρονική στιγμή t1 το σώμα προσκρούει ελαστικά στο άκρο Α της ράβδου. Το σώμα Σ μετά την κρούση αποκτά αντίθετη ταχύτητα ενώ η ράβδος ΑΓ πριν και μετά την κρούση παραμένει ακίνητη σε οριζόντια θέση. Η χρονική διάρκεια επαφής του σώματος Σ και της ράβδου είναι Δt = t2 - t1 = 0,05 s.
Θεωρείστε ότι κατα την διάρκεια της κρούσης η μεταβολή του μήκους του ελατηρίου είναι αμελητέα. Δίνεται g = 10 m/s2.
Δ1) Στην περίπτωση που d = 1 m σχεδιάστε την επιτάχυνση του σώματος συναρτήσει του χρόνου.
Δ2) Υπολογίστε τις δυνάμεις που δέχεται η ράβδος από τα υποστηρίγματα Υ1 και Υ2 κατά την διάρκεια της κρούσης.
Δ3) Υπολογίστε τον ρυθμό μεταβολής της δυναμικής ενέργειας του ελατηρίου όταν αυτό έχει υποστεί την μέγιστη παραμόρφωση στην διάρκεια ταλάντωσης του σώματος Σ.
Δ4) Σχεδιάστε την δύναμη που δέχεται το Σ από το ελατήριο καθώς και την δυναμική ενέργεια του ελατηρίου κατά την Α.Α.Τ. του Σ συναρτήσει της απομάκρυνσης x από τη Θ.Ι. του.
1) ισορροπία Σ : m g = k x0 => 1 10 = 100 x0 => x0 = 0,1 m επιμήκυνση ελατηρίου
k = m ω2 => 100 = 1 ω2 => ω = 10 rad/s T = 2π/10 = π/5 s
x(t) = 0,5 ημ(10t + 3π/2) = 0,5 ημ(10t) συν(3π/2) + 0,5 συν(10t) ημ(3π/2) = - 0,5 συν(10t)
v(t) = 5 συν(10t + 3π/2) = 5 συν(10t) συν(3π/2) - 5 ημ(10t) ημ(3π/2) = 5 ημ(10t)
α(t) = - 50 ημ(10t + 3π/2) = - 50 ημ(10t) συν(3π/2) - 50 συν(10t) ημ(3π/2) = 50 συν(10t)
2) όταν γίνεται η κρούση το σώμα Σ έχει απομάκρυνση από τη θέση ισορροπίας του x = + 0,3 m x(t) = 0,5 ημ(10t + 3π/2) => +0,3 = 0,5 ημ(10t + 3π/2) => ημ(10t + 3π/2) = +0,6 => συν(10t + 3π/2) = + 0,8 και ταχύτητα v = 5 (+0,8) = +4 m/s μετά την κρούση το σώμα Σ αποκτά αντίθετη ταχύτητα v' = - 4 m/s
η δύναμη ελατηρίου : Fελατ = - k (x + x0) = - 100 (0,3 + 0,1) = - 40 Ν
το σώμα κατά την κρούση δέχεται δυνάμεις από τη ΓΗ από το ελατήριο από την ράβδο ΣF = mg + Fελατ + Fράβδου
ρυθμός μεταβολής της ορμής του Σ : Δp / Δt = ΣF => ΣF = ( pτελ - pαρχ ) / Δt = m ( vτελ - vαρχ ) / Δt =>
=> ΣF = 1 kg ( - 4 m/s - 4 m/s ) / 0,05 s => ΣF = - 160 N προς τα επάνω
ΣF = mg + Fελατ + Fράβδου => - 160 = 10 - 40 + Fράβδου => Fράβδου = - 130 Ν προς τα επάνω
η ράβδος δέχεται στο άκρο της Α κατά την κρούση δύναμη από το σώμα Σ 130 Ν κατακόρυφη προς τα κάτω
ροπές ως προς Υ1 : + 130 Ν 0,1 m - 4 kg 10 m/s2 0,4 m + N2 0,8 m = 0 => +13 Nm - 16 Nm + N2 0,8 m = 0 => N2 = 30/8 = 3,75 Ν η ράβδος δέχεται δύναμη 3,75 Ν προς τα επάνω από το στήριγμα Υ2
ροπές ως προς Υ2 : + 130 Ν 0,9 m + 4 kg 10 m/s2 0,4 m + N1 0,8 m = 0 => +117 Nm + 16 Nm + N1 0,8 m = 0 => N1 = 133 / 0,8 = 166,25 Ν η ράβδος δέχεται δύναμη 166,25 Ν προς τα επάνω από το στήριγμα Υ1
3) dU / dt = k (x + x0) v
στην άνω ακραία θέση της ταλάντωσης x = - A = - 0,5 m v = 0 άρα dU / dt = 0
το Σ ποτέ δεν πηγαίνει στην κάτω ακραία θέση της ταλάντωσής του διότι συγκρούεται με την ράβδο όταν x = d = + 0,3 m έχει ταχύτητα v = + 4 m/s οπότε dU/dt = 100 N/m ( + 0,3 m + 0,1 m ) (+ 4 m/s ) = + 160 J/s
4) Fελατ = - k (x + x0) = - 100 (x + 0,1) = - 10 - 100 x - 0,5 m £ x £ + 0,3 m
ΣF = m a => Fελατ + mg = ma => Fελατ + 10 = - 50 ημ(10t + 3π/2) => Fελατ(t) = - 10 - 50 ημ(10t + 3π/2)
μέγιστη δυναμική ενέργεια ελατηρίου όταν το Σ είναι στο κάτω άκρο της ταλάντωσής του U = ½ k (x + x0)2 =
= ½ 100 N/m ( 0,3 m + 0,1 m )2 = 8 J
ελάχιστη δυναμική ενέργεια ελατηρίου όταν το Σ είναι στο άνω άκρο της ταλάντωσής του U = ½ k (-Α + x0)2 =
= ½ 100 N/m ( - 0,5 m + 0,1 m )2 = 8 J

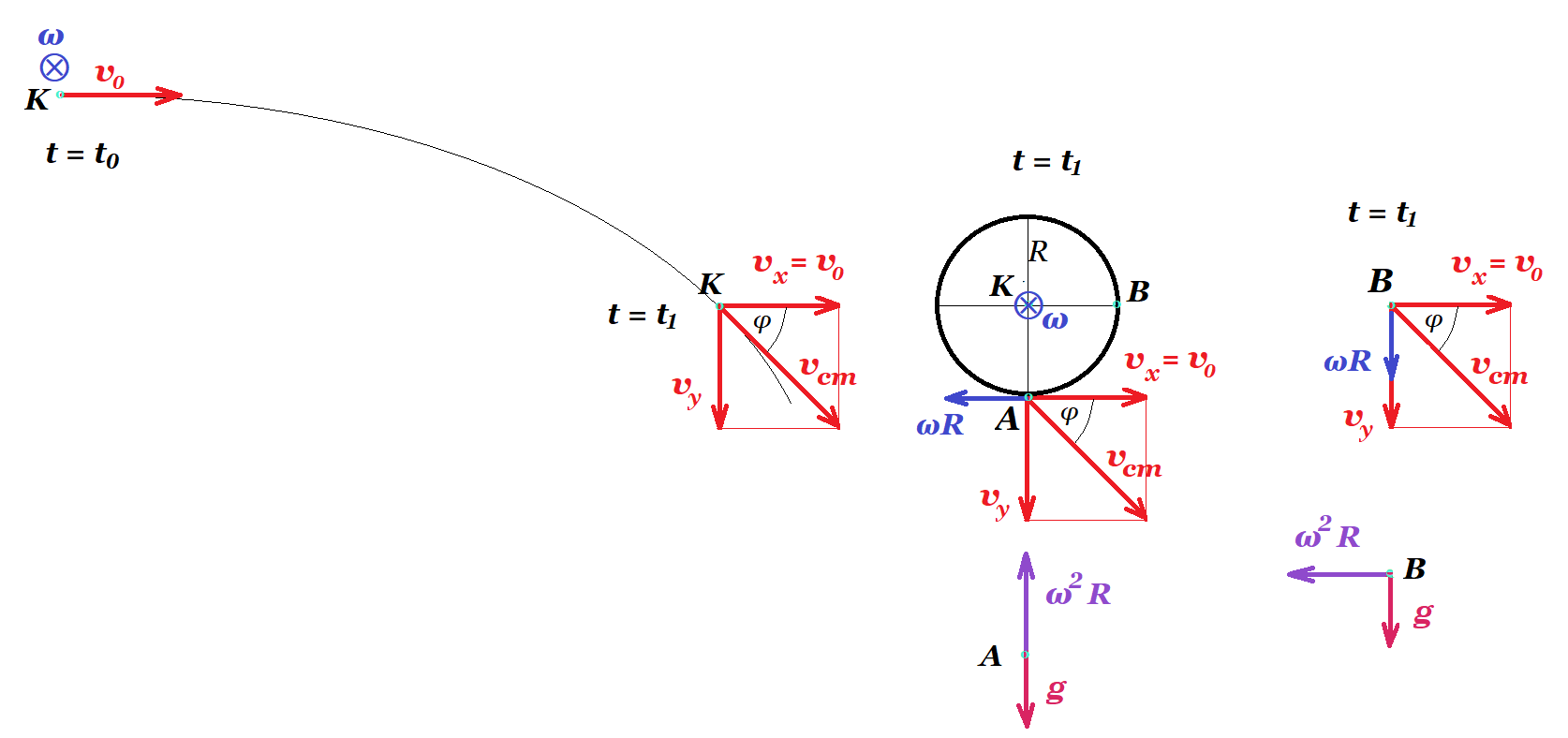
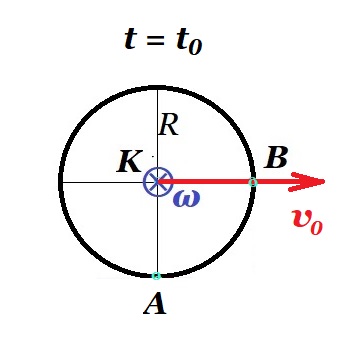 Επίπεδος δίσκος ακτίνας R=0,8m εκτοξεύεται οριζόντια (προς τα δεξιά στο σχήμα) από ορισμένο ύψος, με το επίπεδό του κατακόρυφο, ενώ στρέφεται με γωνιακή ταχύτητα ω. Στην διάρκεια της πτώσης του, το επίπεδό του παραμένει στο ίδιο κατακόρυφο επίπεδο (στο σχήμα, στο επίπεδο της σελίδας), ενώ το κέντρο του Κ (και κέντρο μάζας του) έχει σταθερή επιτάχυνση g. Σε μια στιγμή t1, το σημείο Α, στο άκρο μιας κατακόρυφης ακτίνας, έχει κατακόρυφη ταχύτητα μέτρου 3m/s και κατακόρυφη επιτάχυνση μέτρου 10m/s2. Για την στιγμή αυτή t1, ζητούνται:
Επίπεδος δίσκος ακτίνας R=0,8m εκτοξεύεται οριζόντια (προς τα δεξιά στο σχήμα) από ορισμένο ύψος, με το επίπεδό του κατακόρυφο, ενώ στρέφεται με γωνιακή ταχύτητα ω. Στην διάρκεια της πτώσης του, το επίπεδό του παραμένει στο ίδιο κατακόρυφο επίπεδο (στο σχήμα, στο επίπεδο της σελίδας), ενώ το κέντρο του Κ (και κέντρο μάζας του) έχει σταθερή επιτάχυνση g. Σε μια στιγμή t1, το σημείο Α, στο άκρο μιας κατακόρυφης ακτίνας, έχει κατακόρυφη ταχύτητα μέτρου 3m/s και κατακόρυφη επιτάχυνση μέτρου 10m/s2. Για την στιγμή αυτή t1, ζητούνται:
Δίνεται g=10m/s2.
1. vx = v0 vy = g t => 3 m/s = 10 m/s2 t => t = 0,3 s ω = σταθερά άρα dω / dt = 0
το σημείο Α έχει κατακόρυφη ταχύτητα vy άρα η οριζόντια συνιστώσα της υΑ είναι μηδέν : ωR - vx = 0 => ωR = v0
ω2 R - g = 10 m/s2 => ω2 0,8 m - 10 m/s2 = 10 m/s2 => ω2 = 20 m/s2 / 0,8 m = 25 => ω = 5 rad/s
άρα v0 = ω R = 5 rad/s 0,8 m = 4 m/s οπότε ω2 R = (5 rad/s)2 0,8 m = 20 m/s2 κεντρομόλος επιτάχυνση
2. η ταχύτητα του κέντρου Κ του τροχού : υΚ2 = vx2 + vy2 = 42 + 32 = 52 => υΚ = 5 m/s
3. η ταχύτητα του σημείου Β είναι :
υΒ2 = vx2 + ( ω R + vy )2 = 42 + ( 5 0,8 + 3 )2 = 16 + 72 = 65 => υΒ = √65 m/s
η επιτάχυνση του σημείου Β είναι : aB2 = ( ω2 R )2 + g2 = 202 + 102 => aB = 10√5 m/s2
4. h = 0,5 g t2 => 3,2 = 0,5 10 t2 => t2 = 0,64 => t = 0,8 s
vy = g t => vy = 10 m/s2 0,8 s => vy = 8 m/s υ2 = vx2 + vy2 = 42 + 82 = 42 5 => v = 4√5 m/s
dK/dt = m v a = m v g = 1 kg 4√5 m/s 10 m/s2 = 40√5 J/s
5. L = Δm ω r2 = 10-4 5 0,12 => L = 5 10-6 kg m/s2
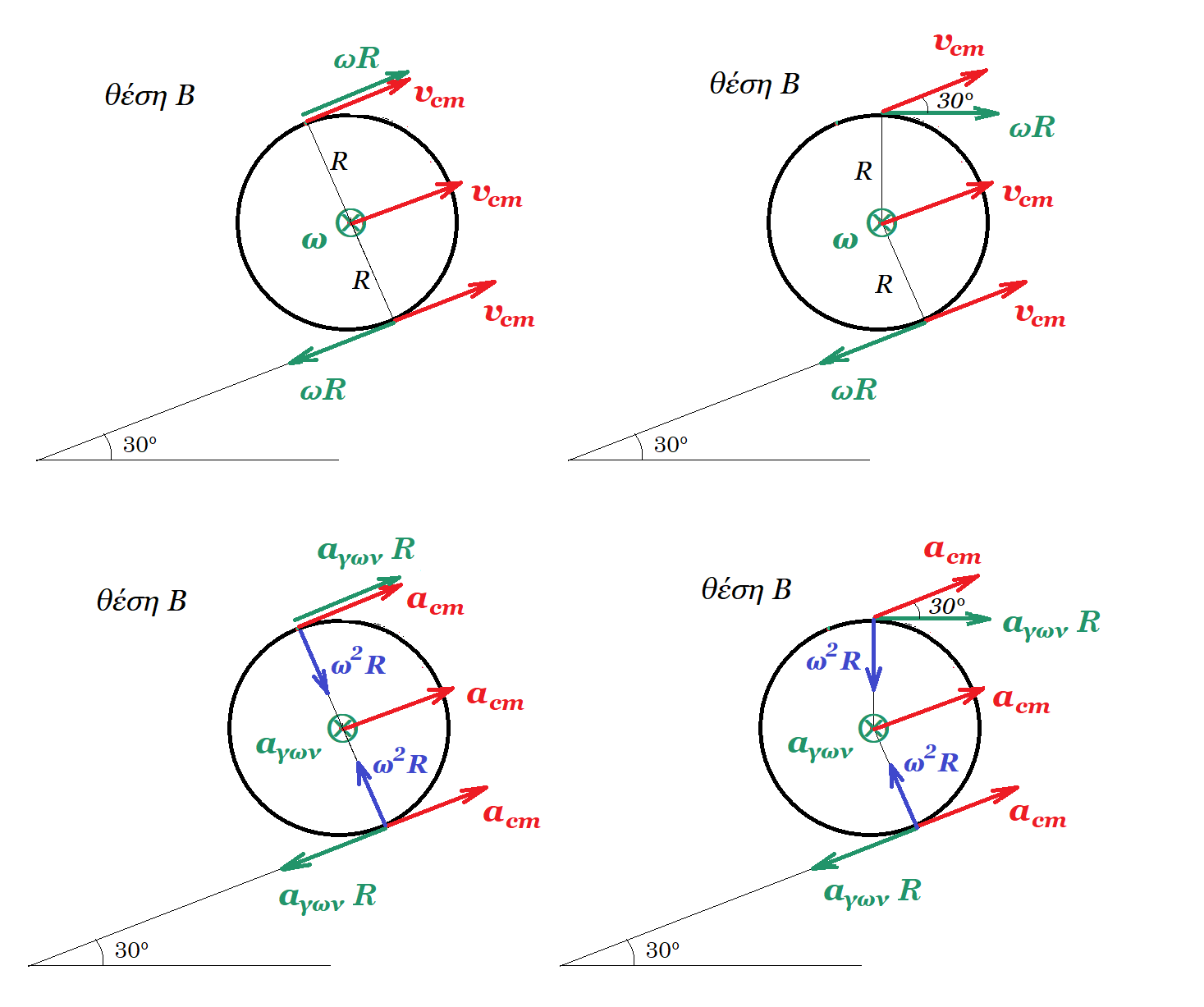
23. ΟΕΦΕ 2008 O αρχικά ακίνητος τροχός του σχήματος που βρίσκεται στη βάση κεκλιμένου επιπέδου ( θέση Α ) γωνίας κλίσεως 30° αποτελείται από ένα λεπτό ομογενή δακτύλιο μάζας 6 kg και ακτίνας 1 m και δύο λεπτές ομογενής ράβδους μήκους 2 m και μάζας 3 kg η κάθε μία που είναι τοποθετημένες κάθετα μεταξύ τους.
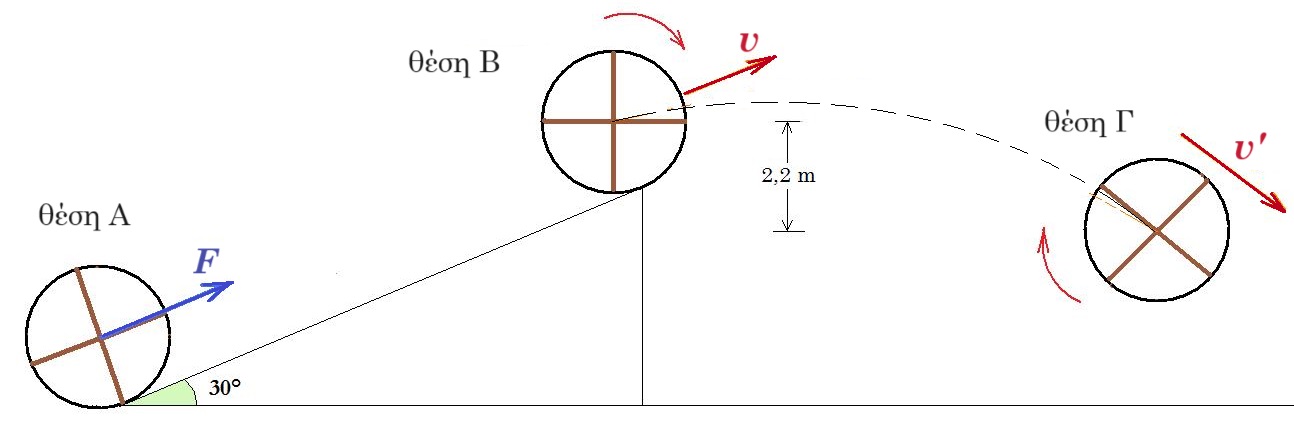 Τη στιγμή t =0 ασκούμε στο κέντρο μάζας Ο του τροχού σταθερή δύναμη F = 100 Ν παράλληλη στο κεκλιμένο επίπεδο και ο τροχός αρχίζει να κυλίεται χωρίς να ολισθαίνει ανερχόμενος στο κεκλιμένο επίπεδο. Όταν ο τροχός φθάσει στην κορυφή του κεκλιμένου επιπέδου ( θέση Β ) έχει εκτελέσει 25/2π περιστροφές. Στη θέση Β καταργούμε την δύναμη F και ο τροχός στη συνέχεια εγκαταλείπει το κεκλιμένο επίπεδο διαγράφοντας καμπύλη τροχιά. Να υπολογίσετε :
Τη στιγμή t =0 ασκούμε στο κέντρο μάζας Ο του τροχού σταθερή δύναμη F = 100 Ν παράλληλη στο κεκλιμένο επίπεδο και ο τροχός αρχίζει να κυλίεται χωρίς να ολισθαίνει ανερχόμενος στο κεκλιμένο επίπεδο. Όταν ο τροχός φθάσει στην κορυφή του κεκλιμένου επιπέδου ( θέση Β ) έχει εκτελέσει 25/2π περιστροφές. Στη θέση Β καταργούμε την δύναμη F και ο τροχός στη συνέχεια εγκαταλείπει το κεκλιμένο επίπεδο διαγράφοντας καμπύλη τροχιά. Να υπολογίσετε :
(α) Το μέτρο της στατικής τριβής που δέχεται που δέχεται ο τροχός από το κεκλιμένο επίπεδο αν ανεβαίνει με γωνιακή επιτάχυνση αγων = 2 rad/s2.
(β) Βρείτε την ταχύτητα του ανώτερου σημείου του τροχού τη στιγμή που αυτός φθάνει στην θέση Β
(γ) Την ταχύτητα του κέντρου μάζας του τροχού τη στιγμή που διέρχεται από τη θέση Γ αν η κατακόρυφη μετατόπιση του κέντρου μάζας του τροχού από τη θέση Β μέχρι τη θέση Γ είναι 2,2 m προς τα κάτω.
(α) R = L/2 = 1 m acm = aγων R = 2 rad/s2 1m => acm = 2 m/s2 επιτάχυνση κέντρου μάζας τροχού
F - Mολική g ημ30° - Τ = Mολική αcm => 100 - 12 10 0,5 - Τ = 12 2 => 40 - Τ = 24 => Τ = 16 Ν
(β) θ = Ν 2π => θ = 25/2π 2π = 25 rad s = θ R = 25 m h = s ημ30° = 25 0,5 =12,5 m
s = ½ α t2 => 25 = ½ 2 t2 => t = 5 s vcm = acm t = 2 m/s2 5 s => vcm = 10 m/s
ω = vcm / R = 10 / 1 => ω = 10 rad/s
v2 = vcm2 + (ωR)2 + 2 vcm ωR συν30° = 102 + 102 + 2 10 10 √3/2 = 102 (2 + 2√3) =>
=> v = 10 √(2+2√3) m/s
(γ) το στερεό στον αέρα δεν δέχεται δύναμη που να δημιουργεί ροπή συνεπώς η γωνιακή ταχύτητά του είναι σταθερή ω = 10 rad/s
διατήρηση ενέργειας Mολική g h + ½ Mολική υ2 = ½ Mολική υ'2 => 10 2,2 + ½ 102 = ½ υ'2 =>
=> 22 + 50 = ½ υ'2 => v'2 = 144 => v' = 12 m/s
πλάγια βολή : υ0,x = v0 συν30° = 10 √3/2 = 5√3 m/s ,
υ0,y = v0 ημ30° = 10 0,5 = 5 m/s
x = υ0,x t = v0 συν30° t
y = h = v0 ημ30° t - ½ g t2 => - 2,2 = 10 ½ t - ½ 10 t2 => 5 t2 - 5 t - 2,2 = 0
Δ = 25 + 44 = 69 = 8,32 t = (5 ± 8,3) / 10 = 1,33 sec ή - 0,33 sec
vy = v0,y - g t = v0 ημ30° - g t = 10 ½ - 10 1,33 = 5 - 13,3 => vy = - 8,3 m/s
v2 = vx2 + vy2 = v0,x2 + vy2 = (5√3)2 + (- 8,3)2 = 75 + 69 = 144 => v = 12 m/s
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
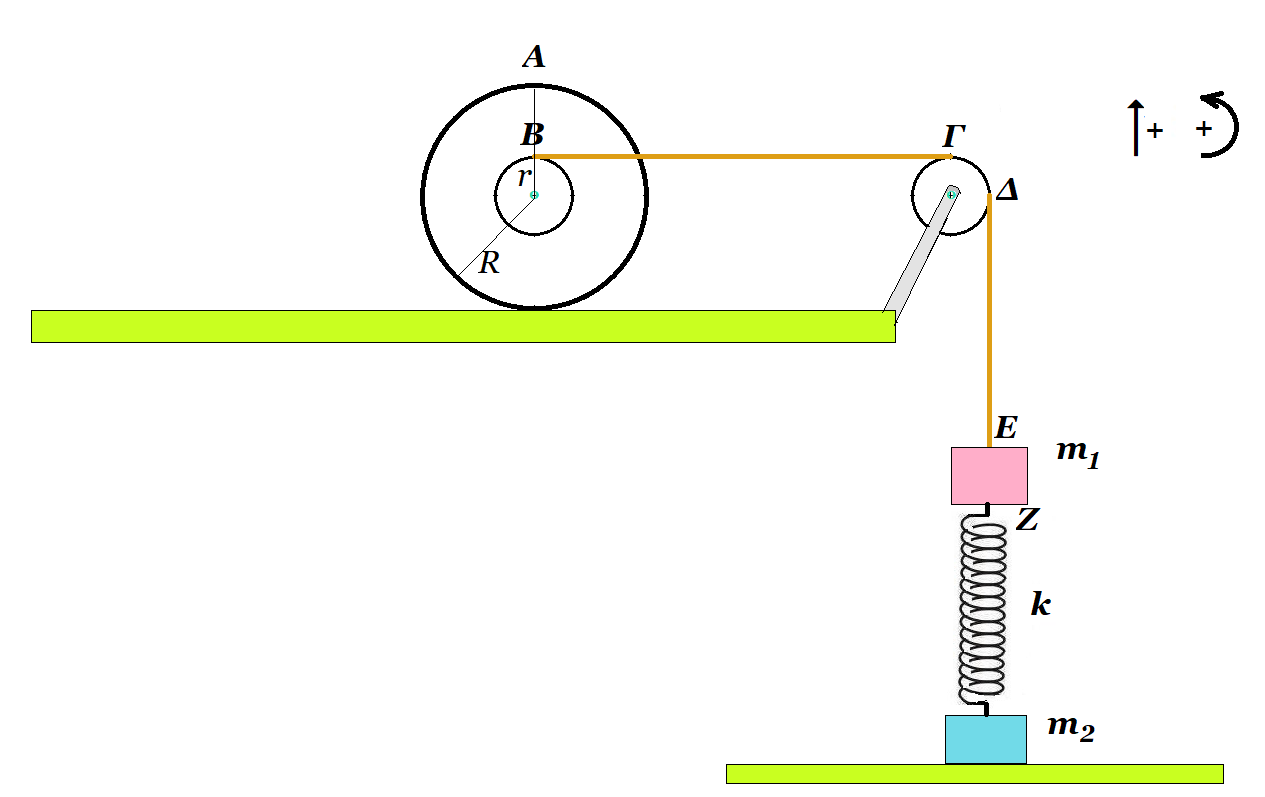
Καρούλι αποτελείται από δυο ομογενείς δίσκους ακτίνας R = 3r και έναν ομογενή κύλινδρο ακτίνας r που έχει τυλιγμένο γύρω του αβαρές και μη εκτατό νήμα και βρίσκεται πάνω σε οριζόντιο τραχύ επίπεδο. Το νήμα διέρχεται από τροχαλία αμελητέας μάζας και το άκρο του είναι προσδεδεμένο σε σώμα μάζας m1 = 4 kg που είναι προσδεδεμένο στο πάνω άκρο κατακόρυφου ιδανικού ελατηρίου σταθεράς k = 100 N/m ενώ στο κάτω άκρο του είναι δεμένο σώμα Σ2 μάζας m2 που είναι σε επαφή με οριζόντιο επίπεδο. Αρχικά τα σώματα του συστήματος είναι ακίνητα με την τιμή της τάσης του νήματος να ισούται οριακά με μηδέν. Τη χρονική στιγμή t0 ασκούμε κατάλληλες δυνάμεις στο καρούλι με αποτέλεσμα την χρονική στιγμή t1 το καρούλι να έχει μετατοπιστεί κατά Δx = 0,3 m προς τα αριστερά εκτελώντας ευθύγραμμη ομαλά μεταβαλλόμενη κίνηση και τα ανώτερα σημεία των δίσκων να έχουν ταχύτητα μέτρου υ = 3 m/s. Επίσης την χρονική στιγμή t1 το νήμα σπάει. Στην διάρκεια του φαινομένου το καρούλι δεν ολισθαίνει και το σώμα Σ2 δεν χάνει την επαφή του με το οριζόντιο επίπεδο. ( √2 = 1,4 ) Να υπολογίσετε :
1) την επιτάχυνση του κέντρου μάζας του καρουλιού από την t0 έως και την t1.
2) το όριο θραύσης του νήματος.
3) το πλάτος ταλάντωσης του σώματος Σ1 μετά την t1.
4) την ελάχιστη τιμή της μάζας του σώματος Σ2.
(1) t = 0 η τάση νήματος T = 0
σώμα (1) : k x0 - m1 g = 0 => k x0 = m1 g => 100 x0 = 40 => x0 = 0,4 m συσπείρωση ελατηρίου
σώμα (2) : Ν - m2 g - k x0 = 0 η δύναμη ελατηρίου προς τα κάτω
δεδομένο : vΑ = 3 m/s επειδή vA = 2 vcm => vcm = 1,5 m/s
ισχύει η σχέση : vcm = acm t = 1,5 m/s
το καρούλι μετατοπίζεται κατά 0,3 m : Δx = 0,5 acm t2 => 0,3 m = 0,5 1,52 / acm => acm = 3,75 m/s2
οπότε : t = vcm / acm = 1,5 m/s / 3,75 m/s2 = 0,4 s
από θεωρία : vΒ = ω r + ω R = ω R/3 + ω R = 4/3 ω R = 4/3 vcm
άρα aΒ = 4/3 acm = 4/3 3,75 m/s2 = 5 m/s2
τα σημεία Β και Γ συνδέονται με το τεντωμένο νήμα άρα έχουν την ίδια επιτάχυνση αΓ = 5 m/s2
τα σημεία Γ και Δ έχουν την ίδια ταχύτητα και την ίδια επιτάχυνση ( η τροχαλία έχει αμελητέα μάζα )
τα σημεία Δ και Ε έχουν την ίδια ταχύτητα και επιτάχυνση λόγω τεντωμένου νήματος συνεπώς το σώμα (1) ανεβαίνει με επιτάχυνση α1 = 5 m/s2 και διανύει σε χρόνο 0,4 s απόσταση
Δx1 = 0,5 a1 t2 = 0,5 5 0,42 = 0,4 m το σώμα (1) μετατοπίζεται κατά 0,4 m με επιτάχυνση 5 m/s2 ενώ συγχρόνως το άνω άκρο Ζ του ελατηρίου μετατοπίζεται προς τα επάνω κατά 0,4 m οπότε το ελατήριο αποκτά το φυσικό του μήκος
(2) στο σώμα (1) ασκούνται οι δυνάμεις : Τ - m1 g + Fελατ = m1 α1 => Τ - 4 10 + k x = 4 5 =>
=> Τ + 100 x = 60 όταν θραύεται το νήμα x = 0 οπότε Τθρ = 60 Ν
(3) ω2 = k / m1 = 100 / 4 => ω = 5 rad/s
όταν αρχίζει την Α.Α.Τ. το σώμα (1) το ελατήριο έχει το φυσικό του μήκος και το σώμα βρίσκεται σε απομάκρυνση 0,4m επάνω από τη θέση ισορροπίας του και έχει ταχύτητα προς τα επάνω v1 = a1 t1 = 5 m/s2 0,4 s = 2 m/s διατήρηση ενέργειας για την ταλάντωση 0,5 100 0,42 + 0,5 4 22 = 0,5 100 A2 => 16 + 16 = 100 A2 => A2 = 2 0,16 => A = 0,4√2 m
x(t) = 0,4√2 ημ(5t + θ) υ(t) = 2√2 συν(5t + θ) α(t) = - 10√2 ημ(5t + θ)
x(0) = 0,4 = 0,4√2 ημ(θ) => ημθ = +√2/2 συνθ = +√2/2 θ = π/4 rad
x(t) = 0,4√2 ημ(5t + π/4) υ(t) = 2√2 συν(5t + π/4) α(t) = - 10√2 ημ(5t + π/4)
ΣF = m1 a => Fελατ - m1g = m1 α => Fελατ - 40 = 4 [- 10√2 ημ(5t + π/4) ] =>
=> Fελατ(t) = 40 - 40√2 ημ(5t + π/4)
στο σώμα (2) ασκείται από το ελατήριο δύναμη : F'ελατ(t) = - 40 + 40 ημ(5t + π/4)
Fελατ = - k (x + x0) = - 100 ( x - 0,4 ) = 40 - 100 x - 0,4√2 m £ x £ + 0,4√2 m
στο σώμα (2) ασκείται από το ελατήριο δύναμη : Fελατ' = - 40 + 100 x - 0,4√2 m £ x £ + 0,4√2 m
(4) σώμα (2) : Ν - m2 g + Fελατ' = 0 => Ν - m2 10 - 40 + 100 x = 0 => Ν = m2 10 + 40 - 100 x
όταν το σώμα (1) είναι στην ανώτερη θέση της ταλάντωσής του ( x = + 0,4√2 m ) το σώμα (2) για να μην χάσει την επαφή του με το οριζόντιο επίπεδο ( Ν ³ 0 ) πρέπει να έχει μάζα :
m2 10 + 40 - 100 (+ 0,4√2 ) ³ 0 => m2 10 ³ - 40 + 40√2 => m2 ³ - 4 + 4√2 = - 4 + 4 1,4 = 1,6 kg m2 ³ 1,6 kg
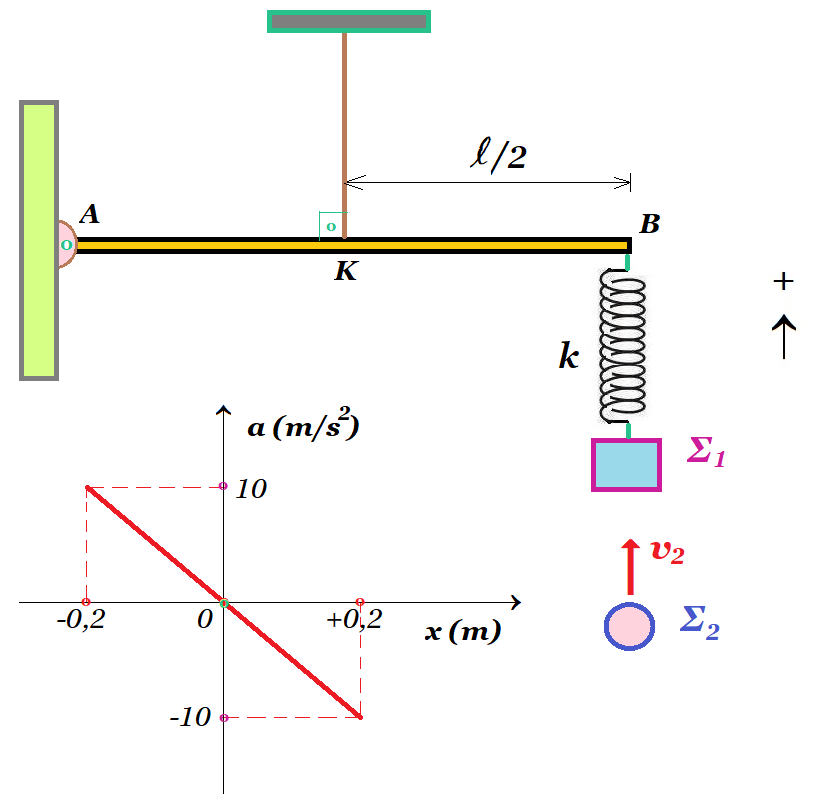
a = - 10/0,2 x => a = - 50 x => ω2 = 50 => ω = 5√2 rad/s
ω2 = k / m1 => k = 50 2 = 100 N/m σταθερά του ελατηρίου
m1 g = k x1 => x1 = 2 10 / 100 = 0,2 m
(m1 + m2) g = k x0 => x0 = 4 10 / 100 = 0,4 m
η κρούση γίνεται όταν το ελατήριο έχει επιμήκυνση 0,4 m που σημαίνει ότι το σώμα βρίσκεται στην κάτω ακραία θέση της ταλάντωσής του άρα έχει μηδενική ταχύτητα
πλαστική κρούση διατήρηση ορμής : m2 v2 = (m1 + m2) u => 2 4 = (2 + 2) u => u = 2 m/s
το συσσωμάτωμα θα ξεκινήσει Α.Α.Τ. τη στιγμή t0 = 0 με ταχύτητα u = 2 m/s και απομάκρυνση x = 0
0,5 (m1 + m2) u2 = 0,5 k A2 => 4 22 = 100 A2 => A = 0,4 m
ω2 = k / (m1 + m2) = 100 / 4 => ω = 5 rad/s
x(t) = 0,4 ημ(5t) υ(t) = 2 συν(5t) α(t) = - 10 ημ(5t)
x(7π/30) = 0,4 ημ(5 7π/30) = 0,4 ημ(7π/6) = 0,4 (-0,5) = - 0,2 m
υ(7π/30) = 2 συν(5 7π/30) = 2 (-√3/2) = - √3 m/s
α(7π/30) = - 10 ημ(5 7π/30) = - 10 (-0,5) = 5 m/s2
Fελατ = - k (x + x0) = - 100 (- 0,2 - 0,4) = + 60 N κατεύθυνση προς τα επάνω
η ράβδος στο άκρο της Β δέχεται από το ελατήριο δύναμη Fελατ' = - 60 N κατεύθυνση προς τα κάτω
ροπές ως προς το μέσον Κ της ράβδου : τ(FΑ) - τ(Fελατ') = 0 =>
=> FΑ (ΚΑ) - Fελατ' (ΚΒ) = 0 => FΑ = Fελατ' = - 60 Ν κατεύθυνση προς τα κάτω
ΣF = 0 => T - Mg - FA - Fελατ' = 0 => T - 20 - 60 - 60 = 0 => T = 140 N τάση νήματος
ΘΕΜΑ Δ

Ομογενής κύλινδρος μάζας Μ και ακτίνας R = 5/π m βρίσκεται σε κεκλιμένο επίπεδο μεγάλου μήκους, γωνίας κλίσεως φ = 30°. Σε σημείο Α της επιφανείας του κυλίνδρου, το οποίο απέχει από την επιφάνεια του κεκλιμένου επιπέδου απόσταση 2R, έχει δεθεί το ένα άκρο αβαρούς μη εκτατού νήματος. Το άλλο άκρο του νήματος έχει δεθεί σε σώμα Σ1 μικρών διαστάσεων και μάζας m1 = 1 kg.
Το νήμα περνά από το αυλάκι τροχαλίας ακτίνας r, η οποία έχει στερεωθεί σε οροφή. Το τμήμα (2) του νήματος είναι παράλληλο προς την επιφάνεια του κεκλιμένου επιπέδου, ενώ το τμήμα (1) κατακόρυφο. Το σύστημα των σωμάτων αυτών ισορροπεί στο ίδιο κατακόρυφο επίπεδο. Ο άξονας του κυλίνδρου είναι κάθετος στο επίπεδο της σελίδας.
Σώμα Σ2 μικρών διαστάσεων και μάζας m2 = 4 kg ισορροπεί δεμένο στο πάνω άκρο κατακόρυφου ιδανικού ελατηρίου σταθεράς k = 100 Ν/m. Το άλλο άκρο του ελατηρίου είναι στερεωμένο στο οριζόντιο δάπεδο. Ο άξονας του ελατηρίου βρίσκεται στην ίδια κατακόρυφη διεύθυνση με τη διεύθυνση του νήματος (1).
Δ1. Να υπολογίσετε τη μάζα Μ του κυλίνδρου και την δύναμη που ασκείται στην τροχαλία στο κέντρο Ο. Μονάδες 6
Τη χρονική στιγμή t0 = 0, κόβουμε ταυτόχρονα τα νήματα (1) και (2).
Αμέσως μετά την t0 = 0, το σώμα Σ1 πέφτει κατακόρυφα ενώ ο κύλινδρος κατέρχεται στο κεκλιμένο επίπεδο με σταθερή επιτάχυνση, εκτελώντας κύλιση χωρίς ολίσθηση.
Κατά τη διάρκεια της κύλισής του ο άξονάς του παραμένει συνεχώς κάθετος στο επίπεδο της σελίδας.
Δ2. Αν τη χρονική στιγμή t1 το σημείο Α, ολοκληρώνει μία πλήρη περιστροφή και έχει ταχύτητα μέτρου υΑ = 20 m/s, να υπολογίσετε το μέτρο της επιτάχυνσης του κέντρου μάζας του κυλίνδρου κάνοντας χρήση των νόμων της κινηματικής κατά την κύλιση στερεών σωμάτων. Μονάδες 7
Το σώμα Σ1 πέφτοντας κατακόρυφα συγκρούεται κεντρικά και πλαστικά με το σώμα Σ2. Το συσσωμάτωμα, αμέσως μετά την πλαστική κρούση εκτελεί φθίνουσα ταλάντωση σε κατακόρυφη διεύθυνση, υπό την επίδραση δύναμης αντίστασης της μορφής Fαντ = -0,2υ (S.I.), όπου υ η αλγεβρική τιμή της ταχύτητας.
Αμέσως μετά την κρούση ο ρυθμός έκλυσης θερμικής ενέργειας στο περιβάλλον είναι ίσος με Pθ = 3,2 J/s. Να υπολογίσετε:
Δ3. το μέτρο της ταχύτητας του συσσωματώματος αμέσως μετά την πλαστική κρούση. Μονάδες 5
Δ4. τη συνολική θερμική ενέργεια που ελευθερώνεται στο περιβάλλον από τη χρονική στιγμή αμέσως μετά την κρούση έως την χρονική στιγμή που η ταλάντωση του συσσωματώματος σταματά. Μονάδες 7
Να θεωρήσετε ότι:
η επιτάχυνση της βαρύτητας g = 10 m/s2,
οι κρούσεις είναι ακαριαίες και κατά την πραγματοποίησή τους δεν έχουμε απώλεια μάζας,
το νήμα δεν ολισθαίνει στο αυλάκι της τροχαλίας.

ισορροπία Σ2 : m2 g = Fελατ = k x0 => 40 = 100 x0 => x0 = 0,4 m
ισορροπία Σ1 : m1 g = Τ1 => Τ1 = 10 Ν
αβαρής τροχαλία : Τ1 = Τ2 => Τ2 = 10 Ν
ισορροπία κυλίνδρου
ροπές ως προς Κ : Στ(Κ) = 0 => Τ2 R = Tτρ R => Tτρ = Τ2 = 10 Ν
ΣFx = 0 => Τ2 + Tτρ - Mg ημ30° = 0 => 10 + 10 - M 10 ½ = 0 => M = 4 kg
ισορροπία τροχαλίας : ΣFx = 0 => F(O),x = T2 συν30° = 10 √3/2 = 5√3 Ν
ΣFy = 0 => F(O),y - T2 ημ30° - T1 = 0 => F(O),y - 10 1/2 - 10 = 0 => F(O),y = 15 N
F(O)2 = F(O),x2 + F(O),y2 = 75 + 225 = 300 => F(O) = 10√3 N
vA = 2 vcm = 20 m/s => vcm = 10 m/s
vcm = ω R => ω = 10 m/s / 5/π m = 2π rad/s Ν = θ/2π => 1 = θ/2π => θ = 2π rad
s = 2πR = 2π 5/π = 10 m = x vcm = acm t
x = ½ acm t2 = ½ vcm t => 10 m = ½ 10 m/s t => t = 2 s acm = vcm / t = 5 m/s2
h = ½ g t2 v12 = 2 g h v1 = g t
m1 v1 = (m1 + m2) u => 1 v1 = (1 + 4) u => v1 = 5u
ισορροπία Σ2 : m2 g = Fελατ = k x0 => 40 = 100 x0 => x0 = 0,4 m αρχική συσπείρωση ελατηρίου
ισορροπία συσσωματώματος : (m1 + m2) g = Fελατ = k Δx => 50 = 100 Δx => Δx = 0,5 m
το συσσωμάτωμα θα εκτελέσει φθίνουσα ταλάντωση με αρχικό πλάτος Α
½ (m1 + m2) u2 + ½ k (x1,2 - x0)2 = ½ k A2 =>
5 u2 + 100 (0,5 - 0,4)2 = 100 A2 => 5 u2 + 1 = 100 A2
ΣF = (m1 + m2) a => - k (x - Δx) - (m1 + m2) g - 0,2 v = (m1 + m2) a =>
=> - k x + k Δx - (m1 + m2) g - 0,2 v = (m1 + m2) a =>
=> - 100 x - 0,2 v = 5 a => - 100 x - 0,2 dx/dt = 5 d2x/dt2 =>
=> 5 d2x/dt2 + 0,2 dx/dt + 100 x => d2x/dt2 + 0,04 dx/dt + 20 x
D = 0,042 - 80 = - 80
ΘΕΜΑ Δ 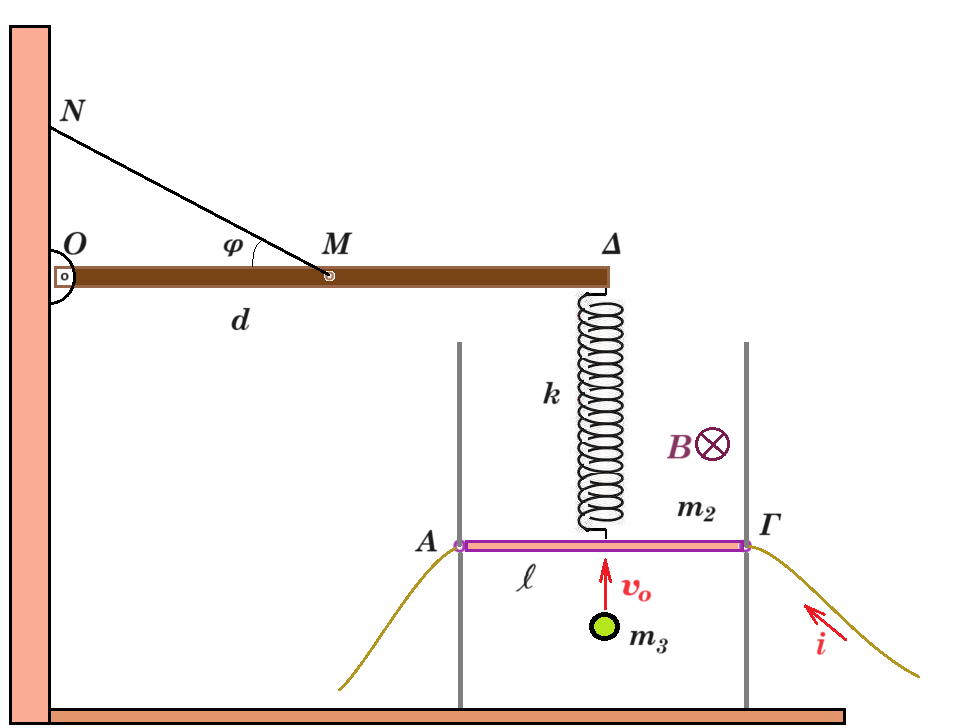
Τα άκρα Α και Γ μιας ομογενούς μεταλλικής ράβδου, μήκους L=0,1 m και μάζας m2=0,8 kg βρίσκονται σε συνεχή επαφή με δύο ακλόνητους, κατακόρυφους και λείους μονωτικούς οδηγούς, οι οποίοι στηρίζονται σε οριζόντιο δάπεδο. Στο μέσο της ράβδου είναι δεμένο με μονωτικό τρόπο, το κάτω άκρο κατακόρυφου ιδανικού ελατηρίου σταθεράς k=100 N/m.
Η ράβδος έχει την δυνατότητα να κινείται χωρίς τριβές πάνω στους κατακόρυφους οδηγούς, παραμένοντας συνεχώς οριζόντια.
Η μεταλλική ράβδος βρίσκεται ολόκληρη μέσα σε οριζόντιο ομογενές μαγνητικό πεδίο έντασης B=2T, του οποίου οι μαγνητικές δυναμικές γραμμές είναι κάθετες στη ράβδο με φορά από τον αναγνώστη προς τη σελίδα. Η ράβδος διαρρέεται από ρεύμα έντασης i=10 A με φορά από το Γ προς το Α . Οι αγωγοί σύνδεσης της ράβδου με την ηλεκτρική πηγή που τροφοδοτεί το σύστημα έχουν αμελητέα μάζα. Η ράβδος ισορροπεί ακίνητη.
Το πάνω άκρο του ελατηρίου είναι συνδεδεμένο στο δεξιό άκρο Δ ομογενούς και ισοπαχούς ξύλινης δοκού ΟΔ μήκους d=2 m το οποίο μπορεί να περιστρέφεται χωρίς τριβές σε κατακόρυφο επίπεδο, γύρω από άρθρωση που βρίσκεται στο αριστερό άκρο του Ο. Η δοκός έχει μάζα m1=4 kg και ισορροπεί ακίνητη και οριζόντια με την βοήθεια του αβαρούς και μη εκτατού νήματος ΝΜ, το ένα άκρο του οποίου είναι δεμένο στο μέσο Μ της δοκού και το άλλο άκρο του Ν σε κατακόρυφο τοίχο.
Το νήμα σχηματίζει με την ράβδο οξεία γωνία φ, για την οποία δίνεται ημφ=0,6 και συνφ=0,8.
Δ1. Να βρεθεί η δύναμη που δέχεται η δοκός από την άρθρωση. (Μονάδες 5)
Τη χρονική στιγμή t0=0 μικρό σώμα μάζας m3=0,2 kg κινούμενο κατακόρυφα με φορά προς τα πάνω με ταχύτητα υ0=10 m/s συγκρούεται και προσκολλάται ακαριαία στο μέσο της μεταλλικής ράβδου ΑΓ, ταυτόχρονα διακόπτουμε το ρεύμα που διαρρέει την μεταλλική ράβδο ΑΓ και απομακρύνουμε τους αγωγούς σύνδεσης από αυτή.
Δ2. Να γράψετε τη χρονική εξίσωση y(t) της απομάκρυνσης του συσσωματώματος m2,3 από τη θέση ισορροπίας του, θεωρώντας θετική φορά την προς τα πάνω. (Μονάδες 5)
Δ3. Τη χρονική στιγμή που για πρώτη φορά η δυναμική ενέργεια της ταλάντωσης του συσσωματώματος m2,3 είναι τριπλάσια της κινητικής ενέργειάς του (Uτ=3Kτ), να υπολογιστεί η διαφορά δυναμικού VΓ - VΑ στα άκρα της μεταλλικής ράβδου. (Μονάδες 5)
Δ4. Να γράψετε τη συνάρτηση Τ(y) του μέτρου της τάσης του νήματος σε σχέση με την απομάκρυνση του συσσωματώματος από την θέση ισορροπίας του. (Μονάδες 5)
Δ5. Να υπολογίσετε τη μέγιστη τιμή της ταχύτητας υ0,max του σώματος m3 για την οποία το νήμα δεν χαλαρώνει και επομένως η δοκός συνεχίζει να ισορροπεί οριζόντια. (Μονάδες 5)
Δίνεται: η επιτάχυνση της βαρύτητας g=10m/s2
Κατά τη διάρκεια της ταλάντωσης η τάση του νήματος δεν υπερβαίνει το όριο θραύσης του.
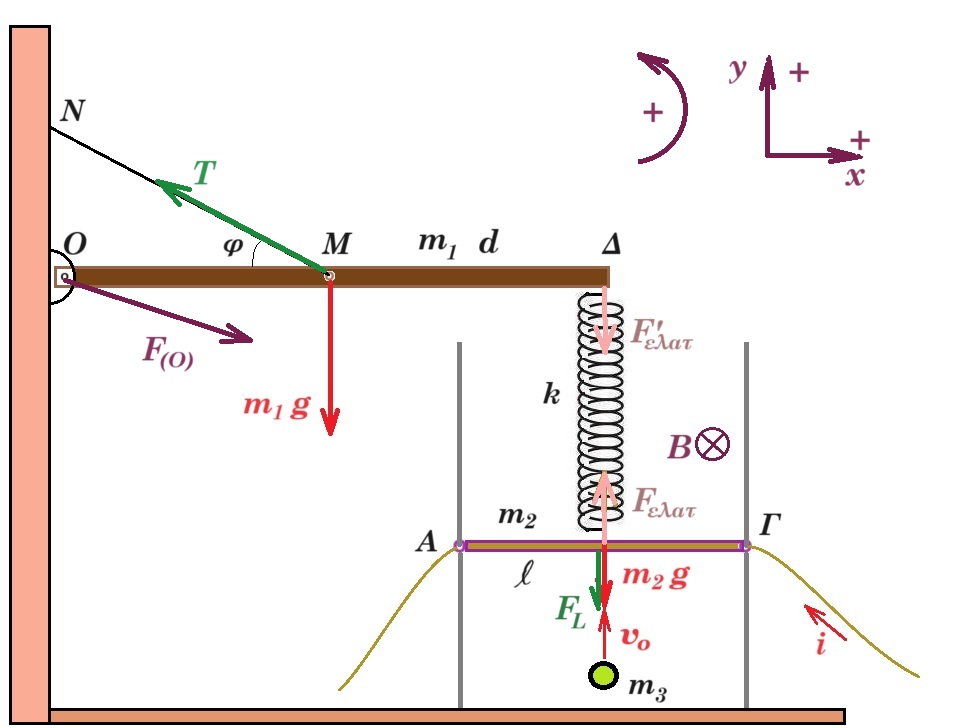
Δ1. ισορροπία αγωγού ΑΓ : Fελατ - m2 g - FL = 0 => k x0 - m2 g - B l i = 0 =>
=> 100 x0 - 0,8 10 - 2 0,1 10 = 0 => x0 = 0,1 m επιμήκυνση ελατηρίου στην ισορροπία
Fελατ' = - Fελατ = - 100 0,1 = - 10 Ν κατεύθυνση προς τα κάτω
ισορροπία δοκού : Στ(Ο) = 0 => Τ ημ30° d/2 - m1 g d/2 - Fελατ' d = 0 =>
=> Τ ½ 1 - 4 10 1 - 10 2 = 0 => Τ = 120 Ν
Tx = T συν30° = 120 √3/2 = 60√3 Ν Ty = T ημ30° = 120 ½ = 60 N
ΣFx = 0 => F(O),x - Tx = 0 => F(O),x = Tx = 60√3 Ν
Στ(M) = 0 => F(O),y d/2 - Fελατ' d/2 = 0 => F(O),y = Fελατ' = 10 N κατεύθυνση προς τα κάτω
πλαστική κρούση διατήρηση ορμής : m3 v0 = (m2 + m3) u => 0,2 10 = (0,8 + 0,2) u => u = 2 m/s
ισορροπία συσσωματώματος : Fελατ - (m2 + m3) g = 0 => k x1 - (m2 + m3) g = 0 =>
=> 100 x1 = 10 => x1 = 0,1 m επιμήκυνση ελατηρίου στην ισορροπία συσσωματώματος
το συσσωμάτωμα ( ο αγωγός ΑΓ με το σώμα m3 ) θα αρχίσει να εκτελεί Α.Α.Τ. με πλάτος Α = 0,1 m και μέγιστη ταχύτητα u = 2 m/s = vmax διότι έχει ταχύτητα και βρίσκεται στη θέση ισορροπίας του
ω2 = k / (m2 + m3) = 100 / 1 => ω = 10 rad/s Α = vmax / ω = 2 m/s / 10 rad/s = 0,2 m
y = 0,2 ημ10t v = 2 συν10t a = - 20 ημ10t
U = 3K = 3/4 E => U = 1/4 E => x = A/2 => ημ10t = 0,5 => συν10t = +√3/2 1η φορά το συσσωμάτωμα ανεβαίνει η ταχύτητα είναι θετική v = 2 (+√3/2) = +√3 m/s
η ράβδος ΑΓ κινείται προς τα πάνω με ταχύτητα +√3 m/s τα ηλεκτρόνια κινούνται προς το άκρο Γ το οποίο φορτίζεται αρνητικά ενώ το άκρο Α φορτίζεται θετικά οπότε η διαφορά δυναμικού ΓΑ είναι : VΓ - VΑ = - ( VΑ - VΓ ) = - B v l = - 2 √3 0,1 Volt = - 0,2√3 V
Fελατ = - k (y - 0,1) = - 100 (y - 0,1) = - 100 y + 10
Fελατ' = - Fελατ = 100 y - 10 - 0,2 m £ y £ + 0,2 m
Στ(Ο) = 0 => Τ ημ30° d/2 - m1 g d/2 + Fελατ' d = 0 =>
=> Τ ½ 1 - 4 10 1 + (100y - 10) 2 = 0 => Τ = 80 - 400y + 40 = 120 - 400y = T(y)
t = 0 y = 0 Fελατ = 10 N Fελατ' = - Fελατ = - 10 N T = 120 N
Fελατ = - k (y - 0,1) = - 100 ( 0,2 ημ10t - 0,1 ) = - 20 ημ10t + 10
Fελατ' = - Fελατ = 20 ημ10t - 10
Στ(Ο) = 0 => Τ ημ30° d/2 - m1 g d/2 + Fελατ' d = 0 =>
=> Τ ½ 1 - 4 10 1 + ( 20 ημ10t - 10 ) 2 = 0 => Τ = 80 - 80 ημ10t + 40 =>
=> Τ(t) = 120 - 80 ημ10t
120 - 400y = T(y) = 0 => y = 0,3 m = A vmax = ω Α = 10 0,3 = 3 m/s
πλαστική κρούση διατήρηση ορμής :
m3 v0 = (m2 + m3) vmax => 0,2 v0 = (0,8 + 0,2) 3 => v0 = 15 m/s
ΘΕΜΑ Δ
Στη διάταξη του σχήματος βλέπουμε τη ράβδο ΚΛ με μάζα m=8kg και μήκος l=1m, αντίστασης R1=0,8Ω που βρίσκεται μέσα σε ομογενές μαγνητικό πεδίο Β=2√2Τ, με φορά όπως στο σχήμα. Για την τροχαλία δίνεται η σχέση των ακτίνων R=2r, ενώ για το στερεό Σ ο εσωτερικός κύλινδρος έχει ακτίνα R και ο εξωτερικός 2R. Tα σώματα έχουν μάζες m1=0,5kg και m2=1kg και το ελατήριο σταθερά k. Αρχικά το σύστημα ισορροπεί με τη βοήθεια αβαρών νημάτων και με τον διακόπτη δ ανοικτό. Η αντίσταση R2=0,2Ω.
Δ1. Να υπολογίσετε τη σταθερά k του ελατηρίου αν αυτό είναι επιμηκυμένο κατά Δl=5cm. (Μονάδες 6)
Τη χρονική στιγμή t=0 κόβουμε το οριζόντιο νήμα και το νήμα που συνδέει τη τροχαλία με τη ράβδο και το νήμα που συνδέει τα Σ1 και Σ2 και αφαιρούμε το Σ1.
Δ2. Να γράψετε την εξίσωση απομάκρυνσης – χρόνου για τις Α.Α.Τ. που κάνει το Σ2 με θετική τη φορά προς τα πάνω. (Μονάδες 6)
Δ3. Να υπολογίσετε το έργο της δύναμης του ελατηρίου από τη χρονική στιγμή t=0 που κόπηκε το νήμα μέχρι τη στιγμή που γίνεται μέγιστη για πρώτη φορά η ταχύτητα του σώματος Σ2. (Μονάδες 6)
Αφήνουμε τη ράβδο ΚΛ να πέσει χωρίς τριβές κατά h=5m μετά το κόψιμο των νημάτων και τότε κλείνουμε ακαριαία τον διακόπτη δ.
Δ4. Ποιο είναι το είδος της κίνηση που θα κάνει η ράβδος μετά το κλείσιμο του διακόπτη ( μονάδες 3) και πόση θερμότητα θα αναπτυχθεί στους αντιστάτες από τη στιγμή που έκλεισε ο διακόπτης μέχρι να διέλθει συνολικό φορτίο ίσο με 20C. (μονάδες 4) (Μονάδες 7)
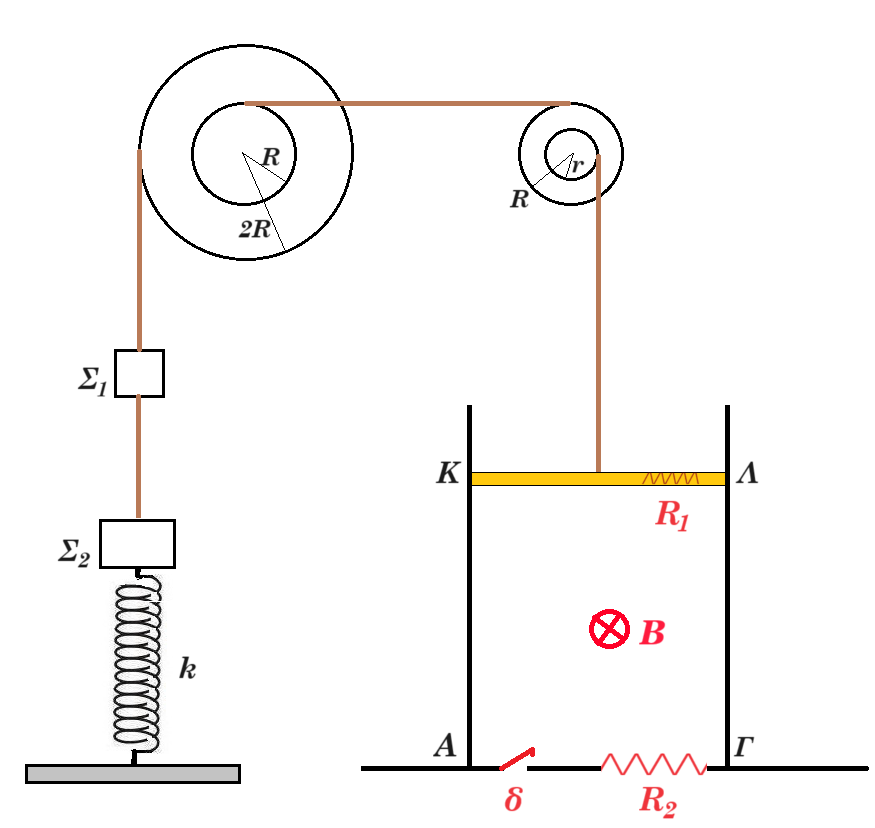
ισορροπία ράβδου : TΚΛ = m g = 80 N = Tr
ισορροπία τροχαλίας : Tr r = TR R => Tr r = TR 2r => 80 = TR 2 => TR = 40 N
ισορροπία στερεού : TR R = T1 2R => 40 = 2 Τ1 => Τ1 = 20 Ν
ισορροπία Σ1 : Τ1 = T2 + m1 g => 20 = T2 + 5 => T2 = 15 N
ισορροπία Σ2 : Τ2 - m2 g + k Δl = 0 => 15 - 10 + k 0,05 => k Δl = + 5 Ν προς τα πάνω επιμήκυνση ελατηρίου Δl = 5 cm k = 5 / 0,05 = 100 N/m
ισορροπία Σ2 μόνο του : - m2 g + k Δl' = 0 => 10 = 100 Δl' => Δl' = 0,1 m συσπείρωση ελατηρίου
k = m2 ω2 => 100 = 1 ω2 => ω = 10 rad/s
x = 0,15 ημ(10t + φ) v = 1,5 συν(10t + φ) a = - 15 ημ(10t + φ)
t = 0 + 0,05 = 0,15 ημφ => ημφ = + 1/3 => φ = 19,5° θετική προς τα πάνω
όταν κόβεται το νήμα το ελατήριο έχει επιμήκυνση Δl = 5 cm άρα δυναμική ενέργεια U = 0,5 k Δl2 = 0,5 100 0,052 = 0,5 100 0,0025 = 0,125 J
όταν το Σ2 έχει μέγιστη ταχύτητα για πρώτη φορά διέρχεται από τη θέση ισορροπίας του με κατεύθυνση προς τα κάτω τότε το ελατήριο είναι συσπειρωμένο κατά Δl' = 0,1 m οπότε έχει δυναμική ενέργεια U = 0,5 k (Δl')2 = 0,5 100 0,12 = 0,5 J
συνεπώς U' - U = 0,5 J - 0,125 J = 0,375 J
h = 0,5 g t2 => 5 = 0,5 10 t2 => t = 1 s v = g t = 10 m/s Eεπαγ = B l v = 2√2 1 10 = 20√2 Volt
B l v = i (R1 + R2) => 2√2 v = i 1 => i = 2√2 v FL = B l i = 2√2 2√2 v = 8v
ΣF = m a => m g - FL = m a => 80 - 8v = 8 a => 10 - v = dv/dt => v - 10 = - dv/dt =>
=> dv/(v - 10) = - dt =>
a = 0 => v = 10 m/s
όταν κλείνει ο διακόπτης η ράβδος έχει στα άκρα της επαγωγική τάση 20√2 Volt και διαρρέται από ρεύμα B l v = i (R1 + R2) => 20√2 = i 1 => i = 20√2 Α οπότε FL = B l i = 2√2 1 20√2 = 80 Ν = το βάρος της άρα ΣF = 0 => α = 0 εκτελεί ευθύγραμμη ομαλή κίνηση με ταχύτητα v = 10 m/s
φορτίο q = i t => 20 C = 20√2 A t => t = 1/√2 s
Q = i2 (R1 + R2) t = 800 1 1/√2 = 400√2 J
ΘΕΜΑ Δ
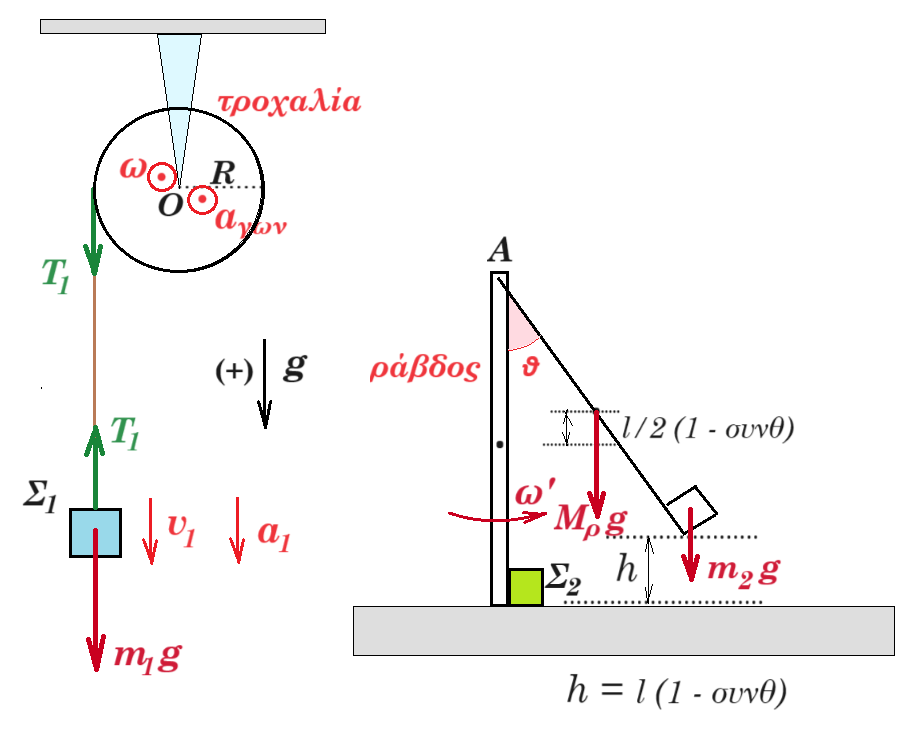
Άκαμπτη, ομογενής και ισοπαχής ράβδος ΑΒ, μήκους l = 1,2 m και μάζας Μρ = 2 Kg, έχει το άκρο της Α αρθρωμένο και ισορροπεί οριζόντια. Η ράβδος μπορεί να στρέφεται, χωρίς τριβές, σε κατακόρυφο επίπεδο γύρω από ακλόνητο οριζόντιο άξονα που διέρχεται από το άκρο της Α.
Στο μέσον Γ της ράβδου ασκείται σταθερή κατακόρυφη δύναμη F με φορά προς τα πάνω, μέτρου F = 80 N. H ράβδος ΑΒ εφάπτεται με το άκρο της Β σε ομογενή τροχαλία, μάζας ΜΤ = 2 Kg και ακτίνας R = 0,5 m, που είναι στερεωμένη σε οροφή και που μπορεί να στρέφεται, χωρίς τριβές, γύρω από ακλόνητο οριζόντιο άξονα που διέρχεται από το κέντρο της και είναι κάθετος στο επίπεδό της.
Αβαρές και μη εκτατό νήμα είναι τυλιγμένο πολλές φορές στο αυλάκι της τροχαλίας και στο ελεύθερο άκρο του είναι δεμένο σώμα Σ1, μικρών διαστάσεων και μάζας m1 = 1 Kg. Η τροχαλία με την επίδραση της τριβής που δέχεται από τη ράβδο ισορροπεί οριακά.
Δ1. Να υπολογίσετε :
i) τον συντελεστή οριακής τριβής μεταξύ ράβδου και τροχαλίας
ii) την δύναμη που δέχεται η ράβδος στην άρθρωση Α. Μονάδες 6
Τη χρονική στιγμή t0 = 0, καταργούμε τη δύναμη F, με αποτέλεσμα η ράβδος να στραφεί γύρω από το άκρο της Α και η τροχαλία να περιστρέφεται γύρω από τον άξονά της. Όταν η ράβδος φθάσει στην κατακόρυφη θέση έχει γωνιακή ταχύτητα μέτρου ω = 5 rad/s, το κάτω άκρο της Β συγκρούεται πλαστικά με ακίνητο σώμα Σ2, μικρών διαστάσεων μάζας m2=1Kg. Αμέσως μετά την κρούση η γωνιακή ταχύτητα της ράβδου είναι ω' = 2 rad/s.
Δ2. Να υπολογίσετε την μεταβολή της στροφορμής στοιχειώδους μάζας Δm = 10-5 kg του κάτω άκρου της ράβδου καθώς και την μεταβολή της ορμής του Σ2 κατά την κρούση. Μονάδες 4
Δ3. Αν το σώμα Σ2 φθάνει σε ύψος 0,24 m και η ράβδος σχηματίζει γωνία θ με την κατακόρυφη όταν ακινητοποιείται στιγμιαία, σε εκείνη τη θέση ποια είναι η συνολική ροπή ως προς την άρθρωση Α του συστήματος << ράβδου - Σ2 >>; Μονάδες 3
Κάτω από το σώμα Σ1 και σε απόσταση h = 1,2 m βρίσκεται σώμα Σ3, μάζας m3 = 3 Kg, το οποίο ισορροπεί στο άνω άκρο κατακόρυφου ιδανικού ελατηρίου σταθεράς k = 100 N / m, η άλλη άκρη του οποίου είναι στερεωμένη σε σώμα Σ4 μάζας m4 = 2 Kg.
Τη χρονική στιγμή t1, το σώμα Σ1 συγκρούεται πλαστικά με το σώμα Σ3 και ταυτόχρονα κόβεται το νήμα. Αμέσως μετά την κρούση το συσσωμάτωμα εκτελεί απλή αρμονική ταλάντωση.
Δ4. Αν το μέτρο της ταχύτητας υ1 του σώματος Σ1, τη χρονική στιγμή t1 που συναντά το σώμα Σ3 έχει μέτρο υ = 2√3 m/s βρείτε την γωνιακή επιτάχυνση αγων περιστροφής της τροχαλίας. Μονάδες 4
Δ5. Αφού γράψετε τη χρονική εξίσωση της απομάκρυνσης του συσσωματώματος βρείτε την δύναμη που δέχεται το σώμα Σ4 από το οριζόντιο δάπεδο καθώς το συσσωμάτωμα ταλαντώνεται. Για ποιο πλάτος ταλάντωσης το Σ4 χάνει την επαφή του με το δάπεδο;
Θεωρήστε χρονική στιγμή t = 0 τη στιγμή της κρούσης και θετική φορά την προς τα κάτω. Μονάδες 8
Δίνονται:
• η επιτάχυνση της βαρύτητας g = 10 m/s2.
• η ροπή αδράνειας ράβδου ως προς άξονα που διέρχεται από το άκρο της Α : Ι(Α) = 1/3 Μρ l2
• η ροπή αδράνειας τροχαλίας ως προς τον άξονα της : Icm(T) = 1/2 MT R2
Να θεωρήσετε ότι:
• οι κρούσεις είναι ακαριαίες και κατά την πραγματοποίησή τους δεν έχουμε απώλεια μάζας.
• η αντίσταση του αέρα θεωρείται αμελητέα για όλα τα σώματα.
• το νήμα δεν ολισθαίνει στο αυλάκι της τροχαλίας.
• το σχήμα δεν είναι υπό κλίμακα.
Δ1.
στην ράβδο ασκούνται βάρος προς τα κάατω, η F προς τα πάνω, η αντίδραση Ν από την τροχαλία προς τα κάτω και από την άρθρωση FA
Στ(Α) = 0 => mg l/2 - F l/2 + N l = 0 => 20 1/2 - 80 1/2 + N = 0 => N = 30 N
ΣFy = 0 => F - N - mg + FA,y = 0 => 80 - 30 - 20 + FA,y = 0 => FA,y = - 30 N προς τα κάτω
τροχαλία : Στ(Ο) = 0 => m1 g R = Ts R => Ts = 10 N οριζόντια αριστερά
στην ράβδο ασκείται δύναμη τριβής Ts' = 10 N οριζόντια προς τα δεξιά μ = Ts' / N = 10 / 30 = 1/3
ΣFx = 0 => Ts' + FA,x = 0 => 10 + FA,x = 0 => FA,x = - 10 N οριζόντια αριστερά
FA2 = 102 + 302 = 1000 => FA = 10√10 N
Δ2.
ΔL = Lμετά - Lπριν = Δm υ' l - Δm υ l = Δm ω' l2 - Δm ω l2 = Δm (ω' - ω) l2 = 10-5 (2 - 5) 1,22 => ΔL = - 4,32 10-5 kg.m2/s
ΔpΣ2 = m2 vμετά - 0 = m2 ω' l = 1 2 1,2 = 2,4 kg.m/s
Δ3.
έστω ότι το σώμα Σ2 ανέρχεται σε ύψος h μετά την κρούση και η ράβδος σχηματίζει γωνία θ με την κατακόρυφη τότε h = l - l συνθ = l (1 - συνθ) => 0,24 = 1,2 (1 - συνθ) => συνθ = 0,8
συνθ = 0,8 ημθ = 0,6
στη θέση αυτή dL/dt = Στ(Α) = Μρ g l/2 ημθ + m2 g l ημθ = 20 0,6 0,6 + 10 1,2 0,6 = 24 0,6 = 14,4 Νm = 14,4 kg m2/s2
Δ4.
v1 = a1 t h = 0,5 a1 t2 => h = 0,5 υ1 t => 1,2 = 0,5 2√3 t => t = 1,2/√3 s => t = √0,48 s
v1 = a1 t => 2√3 = a1 1,2/√3 => a1 = 2 3 / 1,2 = 60 / 12 = 5 m/s2
αγων = α1 / R = 5 / 0,5 = 10 rad/s2 γωνιακή επιτάχυνση τροχαλίας
Δ5.
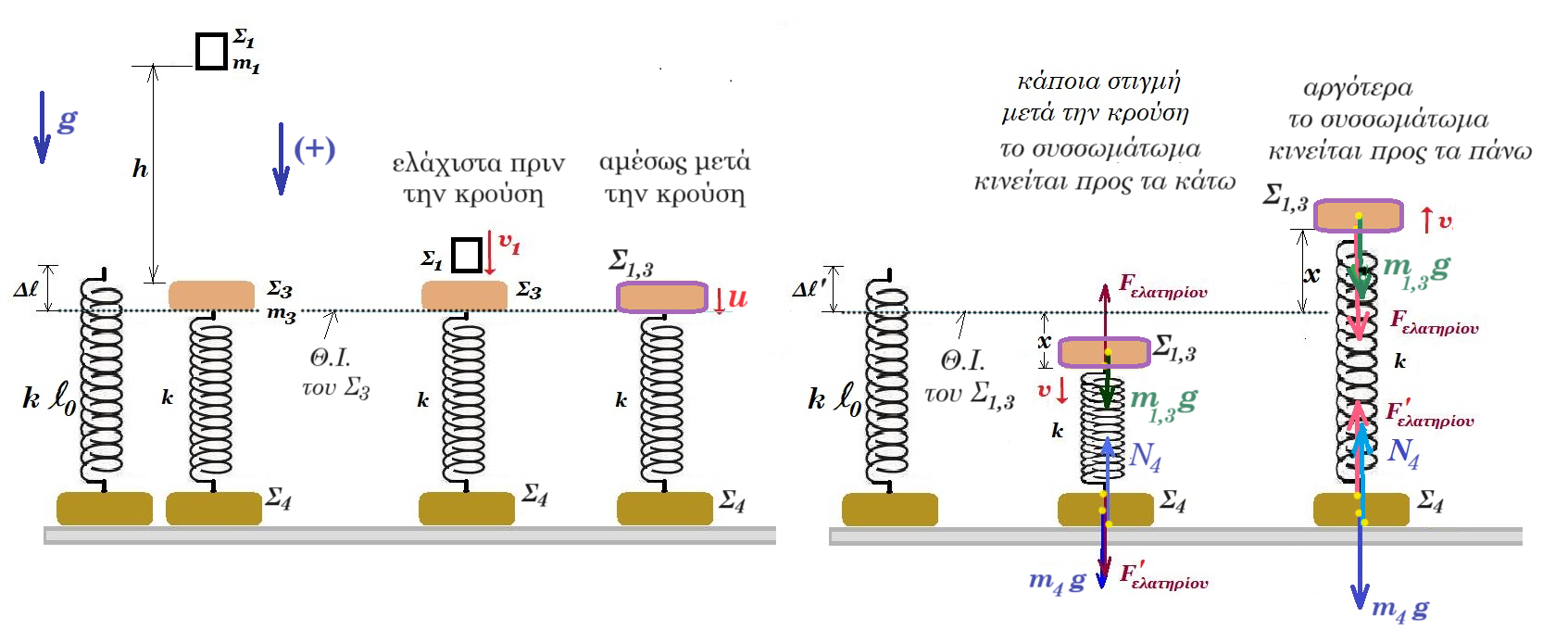
ισορροπία Σ3 : m3 g = k Δl => 3 10 = 100 Δl => Δl = 0,3 m συσπείρωση
ισορροπία Σ1,3 : m1,3 g = k Δl => 4 10 = 100 Δl => Δl' = 0,4 m συσπείρωση
διατήρηση ορμής πλαστική κρούση : m1 v1 = m1,3 u => 1 √12 = 4 u => u = √3/2 m/s
0,5 k Δl2 + 0,5 m1,3 u2 = 0,5 k A2 => 100 0,12 + 4 3/4 = 100 A2 => 1 + 3 = 100 A2 => A2 = 0,04 => A = 0,2 m
k = m1,3 ω2 => 100 = 4 ω2 => ω = 5 rad/s
x = 0,2 ημ(5t + θ) - 0,1 = 0,2 ημθ => ημθ = - 0,5 => θ = π + π/6 = 7π/6
οπότε συν(7π/6) = - √3/2 < 0 απορρίπτεται διότι υ > 0 προς τα κάτω κίνηση
άρα θ = 2π - π/6 = 11π/6 οπότε συνθ = + √3/2 > 0 υ > 0
x(t) = 0,2 ημ(5t + 11π/6) υ(t) = 1 συν(5t + 11π/6) α(t) = - 5 ημ(5t + 11π/6)
x(t) = 0,2 ημ(5t + θ) v(t) = 1 συν(5t + θ) a(t) = - 5 ημ(5t + θ)
ΣF = m1,3 a => m1,3 g + Fελατ = m1,3 a => 40 + Fελατ = 4 ( - 5 ημ(5t + θ) ) =>
=> Fελατ(t) = - 40 - 20 ημ(5t + θ) ή Fελατ(x) = - 100 (0,4 + x) όπου - 0,2m £ x £ +0,2m τη στιγμή t = 0 x = - 0,1 m ημθ = - 0,5 το ελατήριο είναι συσπειρωμένο κατά Δl = 0,3 m άρα η δύναμη ελατηρίου είναι Fελατ = - 100N/m 0,3 m = - 30 N κατακόρυφη προς τα πάνω ( θετική προς τα κάτω )
στο κάτω άκρο του ελατηρίου η δύναμη έχει εξίσωση F'ελατ = 40 + 20 ημ(5t + θ) = 100 (0,4 + x)
οπότε το σώμα Σ4 δέχεται δυνάμεις : ΣF = 0 => m4 g - N4 + F'ελατ = 0 =>
=> 20 - N4 + 40 + 20 ημ(5t + 11π/6) = 0 => Ν4(t) = 60 + 20 ημ(5t + 11π/6)
Ν4(x) = 60 + 100.x - 0,2m £ x £ +0,2m
τη στιγμή t = 0 x = - 0,1 m ημθ = - 0,5 το ελατήριο είναι συσπειρωμένο κατά Δl = 0,3 m άρα η δύναμη ελατηρίου είναι Fελατ = - 100N/m 0,3 m = - 30 N κατακόρυφη προς τα πάνω ( θετική προς τα κάτω ) το Σ4 δέχεται από το ελατήριο δύναμη 30 Ν προς τα κάτω επίσης δέχεται το βάρος του 20 Ν προς τα κάτω συνεπώς η αντίδραση Ν4 από το δάπεδο είναι 50 Ν προς τα πάνω πράγματι
Ν4 = 60 + 20 ημ(5t + 11π/6) = 60 + 20 (- 0,5) = + 50 Ν
το Σ4 για να χάσει την επαφή του με το δάπεδο πρέπει να μηδενισθεί η Ν4 αυτό συμβαίνει όταν το πλάτος ταλάντωσης του συσσωματώματος Σ1,3 γίνεται ίσο με Α = 0,4m + 0,2m = 0,6m πρέπει να βρεθεί το Σ1,3 πάνω από τη Θ.Ι. του ( 0,4m ) και να έχει το ελατήριο επιμήκυνση ( 0,2m ) ώστε η δύναμη ελατηρίου για το Σ1,3 να ισούται με 20 Ν = 100 Ν/m 0,2 m με φορά προς τα κάτω ενώ για το Σ4 η δύναμη ελατηρίου ισούται με 20 Ν με φορά προς τα πάνω και έτσι εξουδετερώνεται το βάρος του Σ4
![]()
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
το ιδανικό ελατήριο έχει σταθερά k = 100 N/m το σώμα Σ μάζα m = 1 kg ισορροπεί ακίνητο
η ράβδος ΚΛ έχει μήκος l = 1 m μάζα M = 0,5 kg ισορροπεί οριζόντια μέσα σε οριζόντιο ομογενές μαγνητικό πεδίο εντάσεως Β = 0,1 Τ
το αβαρές νήμα έχει σταθερό μήκος, συνδέει το σώμα Σ με τη ράβδο, είναι παράλληλο στο κεκλιμένο επίπεδο γωνίας θ διέρχεται από το αυλάκι τροχαλίας που είναι σταθερά στερεωμένη

Μετακινούμε το σώμα Σ κατά τον άξονα του ελατηρίου συσπειρώνοντας αυτό κατά Δl = 0,2 m και το αφήνουμε ελεύθερο να κινηθεί τη στιγμή t=0. Το σώμα Σ εκτελεί Α.Α.Τ. σταθεράς D = k οπότε η ράβδος ΚΛ μέσω του νήματος ακολουθώντας την κίνηση του Σ κινείται σε κατακόρυφο επίπεδο χωρίς να στρέφεται μέσα στο μαγνητικό πεδίο κάθετα στις δυναμικές γραμμές του.
Στα άκρα της ράβδου υπάρχουν πολύ μικρές ακίδες. Κατεβαίνοντας η ράβδος ακουμπά την οριζόντια επιφάνεια υγρού στα σημεία Κ' και Λ' του σχήματος, οπότε δημιουργούνται κύματα στην επιφάνεια του υγρού με πλάτος Α = 0,1 m. Σε ένα σημείο Ρ της επιφάνειας που απέχει r1 = 0,8 m r2 = 1,1 m από τα Κ' και Λ' αντίστοιχα συμβάλουν κύματα.
Βρείτε την χρονική εξίσωση της απομάκρυνσης του σώματος Σ και τον ρυθμό μεταβολής της κινητικής του ενέργειας.
Βρείτε την τάση στα άκρα της ράβδου καθώς κινείται.
![]()