ΓΡΑΠΤΗ ΔΟΚΙΜΑΣΙΑ Γ΄ ΛΥΚΕΙΟΥ ΦΥΣΙΚΗ
ονοματεπώνυμο : ημερομηνία :
ΘΕΜΑ Α
Να επιλέξετε τη σωστή απάντηση. Επιλογή μίας απάντησης.
(Α 1)
Αν το πλάτος Α μιας φθίνουσας ταλάντωσης μεταβάλλεται με το χρόνο σύμφωνα με τη σχέση Α=Αοe-Λt , όπου Αο το αρχικό πλάτος και Λ μια θετική σταθερά, τότε:
(α) ο λόγος δύο διαδοχικών μέγιστων απομακρύνσεων προς την ίδια κατεύθυνση μειώνεται με το χρόνο.
(β) η αντιτιθέμενη δύναμη είναι ανάλογη της απομάκρυνσης από τη θέση ισορροπίας.
(γ) το πλάτος της ταλάντωσης είναι σταθερό.
(δ) η μηχανική ενέργεια του συστήματος ελαττώνεται με την πάροδο του χρόνου.
Μονάδες 5
(Α 2)
Στη διάταξη του σχήματος - πάνω σε οριζόντιο λείο επίπεδο - οι αγωγοί ΑΓ, ΓΗ, ΗΖ δεν έχουν ωμική αντίσταση. Η χάλκινη ράβδος ΛΜ έχει μήκος l, μάζα m, ωμική αντίσταση r, συνδέεται με δύο όμοια ιδανικά ελατήρια σταθεράς k. Η ράβδος ηρεμεί ώστε τα ελατήρια έχουν το φυσικό τους μήκος. Η όλη διάταξη είναι μέσα σε ομογενές μαγνητικό πεδίο εντάσως Β. Ο διακόπτης δ είναι ανοικτός. Δεν υπάρχουν τριβές ούτε αντίσταση αέρα. Απομακρύνουμε τη ράβδο προς τα δεξιά κατά Α0. Τη στιγμή t=0 αφήνουμε ελεύθερη τη ράβδο από τη θέση x = +A0 και συγχρόνως κλείνουμε τον διακόπτη. Η ράβδος θα εκτελέσει :
(α) ΑΑΤ με εξίσωση της απομάκρυνσης από τη θέση ισορροπίας: x(t) = Α0ημ{ (2.k/m)½.t + π/2 }
(β) φθίνουσα αρμονική ταλάντωση με σταθερά απόσβεσης b = B2.l2 / (r + R).
Μονάδες 5
(Α 3)
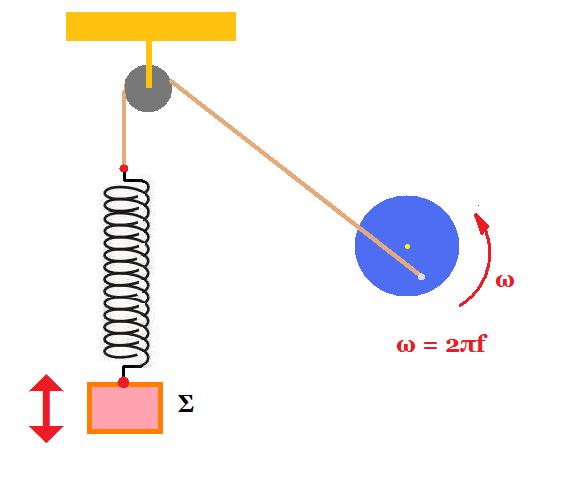Σώμα μάζας m εκτελεί εξαναγκασμένη ταλάντωση μέσα σε ρευστό από το οποίο δέχεται δύναμη της μορφής F' = - b.υ με b = σταθερά απόσβεσης. Ο τροχός περιστρέφεται με συχνότητα f. Αν η σταθερά του ελατηρίου είναι k τότε :(α) το σώμα εκτελεί ταλάντωση με συχνότητα (k/m)½/2π
(β) η ταλάντωση του σώματος παρουσιάζει διακρότημα.
(γ) το σώμα εκτελεί ταλάντωση με συχνότητα f .
(δ) το πλάτος της ταλάντωσης του σώματος μειώνεται σε σχέση με το χρόνο.
Μονάδες 5
(Α 4)
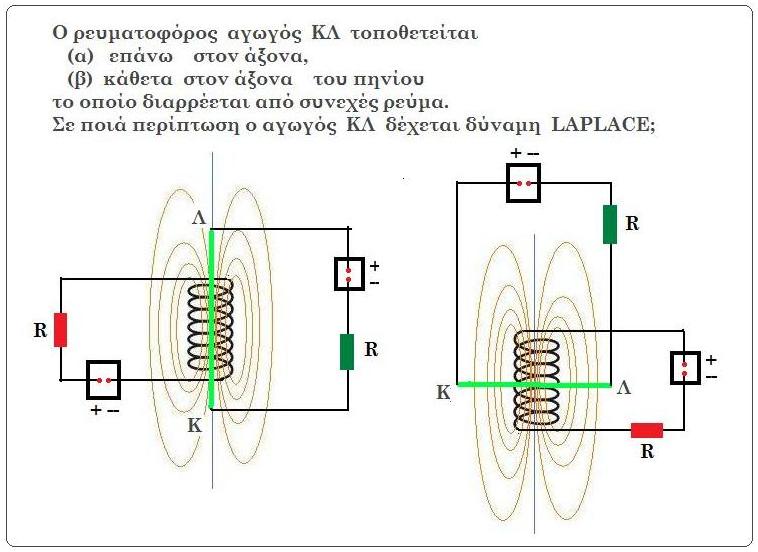Μονάδες 5
(Α 5)
Να γράψετε στο τετράδιό σας το γράμμα κάθε πρότασης και δίπλα σε κάθε γράμμα τη λέξη Σωστό, για τη σωστή πρόταση, και τη λέξη Λάθος, για τη λανθασμένη.
(α) Το μέτρο της έντασης του μαγνητικού πεδίου σε κάθε σημείο γύρω από ευθύγραμμο ρευματοφόρο αγωγό πολύ μεγάλου μήκους μειώνεται καθώς απομακρυνόμαστε από τον αγωγό.
(β) Οι δυναμικές γραμμές του μαγνητικού πεδίου που δημιουργείται σε ένα πηνίο που διαρρέεται με ρεύμα εντάσεως i είναι ανοικτές.
(γ) Κυκλικό χάλκινο σύρμα έχει μήκος l, διαρρέεται με συνεχές ρεύμα εντάσεως i, στο κέντρο του η ένταση του μαγνητικού πεδίου είναι 10-3 Τesla. Mε το σύρμα δημιουργούμε 10 ομόκεντρους κύκλους και τροφοδοτούμε με το ίδιο ρεύμα i. Η ένταση του μαγνητικού πεδίου στο κέντρο των κύκλων θα είναι 0,1 Τesla.
(δ) αν η απομάκρυνση ενός σώματος που εκτελεί απλή αρμονική ταλάντωση δίνεται από τη σχέση x=5.ημ4πt (S.I.), τότε η γωνιακή συχνότητα της ταλάντωσης είναι 4rad/s.
(ε)
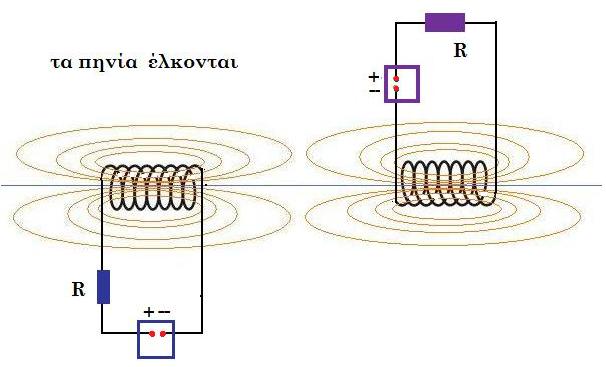
Μονάδες 5
ΘΕΜΑ Β
(Β 1)
Το πλάτος Α μιας φθίνουσας ταλάντωσης μεταβάλλεται με το χρόνο t σύμφωνα με τη σχέση Α=Αοe-Λt, όπου Αο το αρχικό πλάτος και Λ μια θετική σταθερά. Ο απαιτούμενος χρόνος μέχρι το πλάτος της ταλάντωσης να γίνει Αο/2 είναι :
(α) ln2 / 2Λ, (β) ln2 / Λ, (γ) 2.ln2 / Λ.
Να αιτιολογήσετε την απάντησή σας. Μονάδες 5
(Β 2)
Θεωρούμε πάνω σε λείο οριζόντιο επίπεδο, δύο παράλληλους ευθύγραμμους αγωγούς οι οποίοι διαρρέονται από συνεχή ομόρροπα ρεύματα i1 και i2 και απέχουν απόσταση d.
(α) Να βρεθούν σημεία του επιπέδου των αγωγών όπου η ένταση του μαγνητικού πεδίου ισούται με μηδέν.
(β) Μεταξύ των αγωγών θεωρούμε μεταλλική ράβδο μήκους l η οποία είναι παράλληλη στους αγωγούς και διαρρέεται από συνεχές ρεύμα Ι αντίρροπο ως προς τα i1 και i2. Σε ποια απόσταση από τους αγωγούς πρέπει να τοποθετηθεί η ράβδος έτσι ώστε να ισορροπεί;
(γ) Έστω r1 , r2 οι αποστάσεις της ράβδου από τους αγωγούς που διαρρέονται από τα ρεύματα i1 και i2 αντίστοιχα στη θέση ισορροπίας. Μετακινούμε την ράβδο παράλληλα κατά x, τέτοιο ώστε : x << r1 , x << r2 Δείξτε ότι θα κάνει Α.Α.Τ. με σταθερά επαναφοράς :
D = 10-7 Ν/Α2 . 2.I .l .( i2 + i1 )/ r2 .r1
Να αιτιολογήσετε την απάντησή σας. Μονάδες 5 + 5 + 5
(Β 3)
Ελατήριο κάνει εξαναγκασμένες ταλαντώσεις έχει σταθερά k = 162 Ν/m & το σώμα μάζα m = 0,5 kg. Το σώμα σε χρόνο t = 10π s διέρχεται 90 φορές από τη θέση ισορροπίας του. Τότε η κυκλική συχνότητα του διεγέρτη τροχού είναι:
(α) 9 rad/s (β) 18 rad/s, (γ) 17 rad/s
Να αιτιολογήσετε την απάντησή σας. Μονάδες 5
ΘΕΜΑ Γ
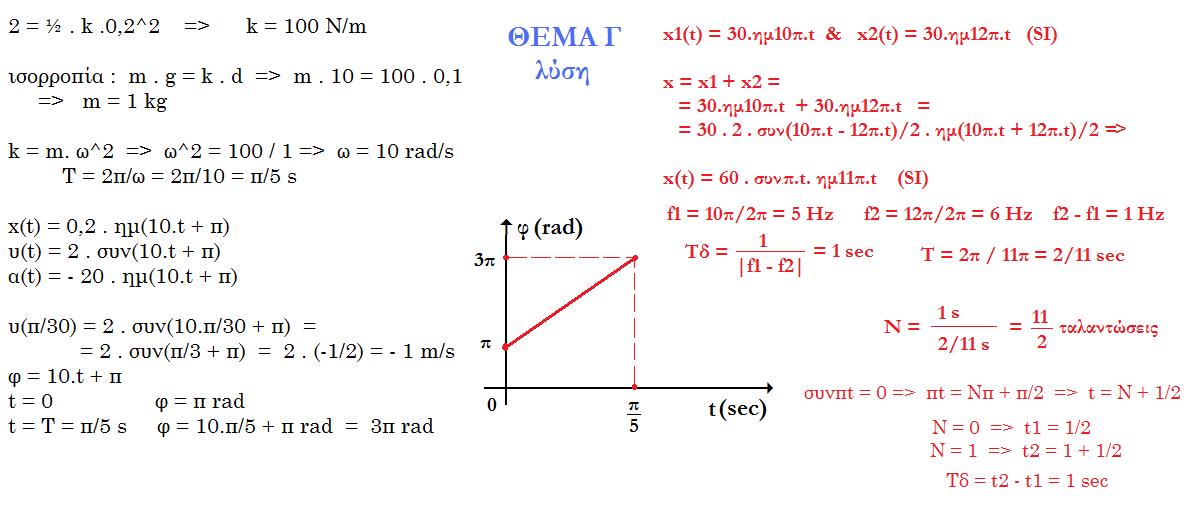
Γ1. Κατακόρυφο ελατήριο σταθεράς k έχει το πάνω άκρο του στερεωμένο σε οροφή. Στο κάτω άκρο του ελατηρίου έχει προσδεθεί σώμα μάζας m που ισορροπεί. Στη θέση ισορροπίας το ελατήριο έχει επιμηκυνθεί κατά d = 0,1 m. Το σύστημα εκτελεί απλή αρμονική ταλάντωση με ενέργεια E = 2 J και η χρονική εξίσωση απομάκρυνσης είναι x(t) = 0,2 ημ(ωt + π) (SI). Θετική έχει θεωρηθεί η κατακόρυφη προς τα κάτω φορά. Να βρείτε:
(α) την ταχύτητα υ του σώματος, τη χρονική στιγμή t = π/30 s. Δίνεται : g = 10 m/s2.
(β) να παραστήσετε γραφικά τη φάση φ της ταλάντωσης συναρτήσει του χρόνου t, στο χρονικό διάστημα από t0 = 0 ως t = T Μονάδες 10 + 5
Γ2. Σώμα μάζας m εκτελεί ταλάντωση εξ'αιτίας της σύνθεσης δύο απλών ταλαντώσεων που γίνονται περί το ίδιο σημείο, πάνω στην ίδια διεύθυνση και οι χρονικές εξισώσεις της απομάκρυνσης δίνονται από τις σχέσεις: x1(t) = 30.ημ10π.t & x2(t) = 30.ημ12π.t (SI)
(α) εκφράστε την απομάκρυνση από τη θέση ισορροπίας συναρτήσει του χρόνου,
(β) βρείτε πόσες ταλαντώσεις λαμβάνουν χώρα μεταξύ δύο διαδοχικών μηδενισμών του πλάτους της ταλάντωσης του σώματος. Μονάδες 5 + 5
ΘΕΜΑ Δ
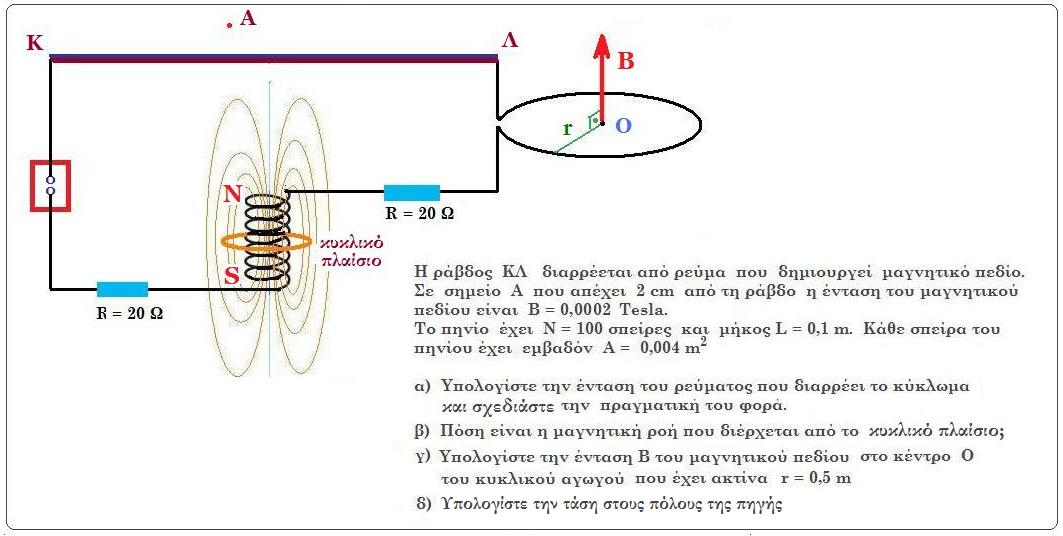
Μονάδες 5 + 10 + 5 + 5
