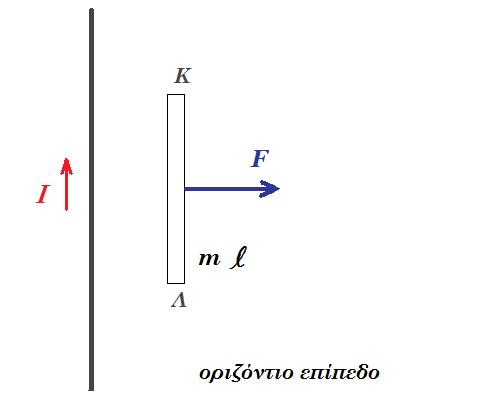

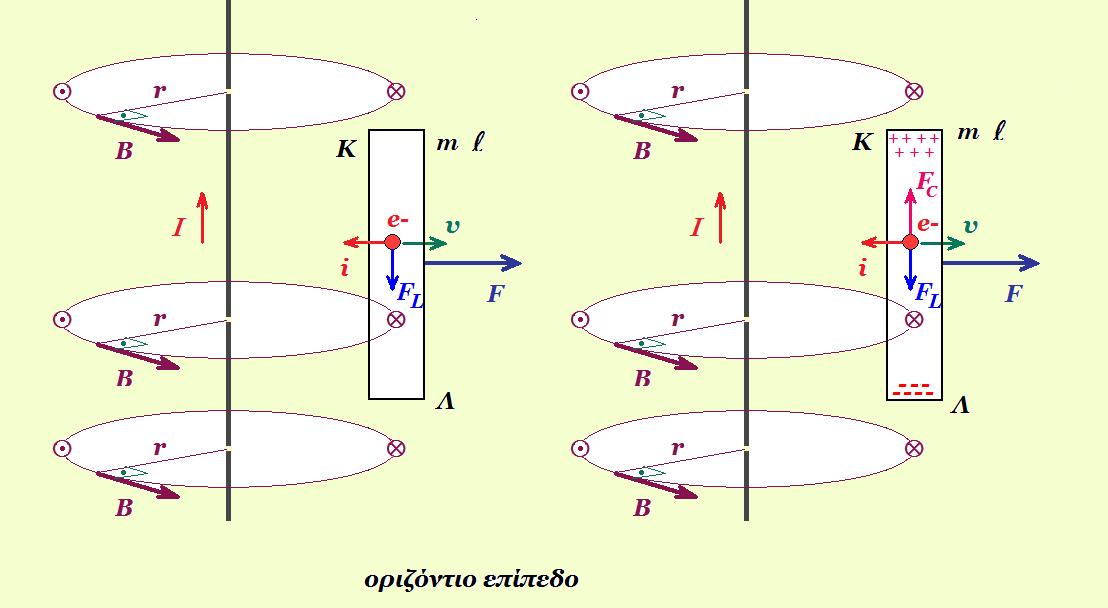
Στο κύκλωμα του σχήματος, οι κατακόρυφοι μεταλλικοί οδηγοί 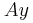 και και 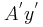 έχουν αμελητέα αντίσταση, με τα άκρα τους A και A' να συνδέονται με πηγή Η.Ε.Δ. Ε=12V και εσωτερικής αντίστασης r=1Ω. έχουν αμελητέα αντίσταση, με τα άκρα τους A και A' να συνδέονται με πηγή Η.Ε.Δ. Ε=12V και εσωτερικής αντίστασης r=1Ω. Τα σημεία Μ και Ν είναι γεφυρωμένα με σύρμα αντίστασης 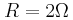 μέσω διακόπτη Δ, ο οποίος είναι αρχικά ανοικτός. μέσω διακόπτη Δ, ο οποίος είναι αρχικά ανοικτός. Η ράβδος ΚΛ έχει μάζα 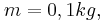 μήκος μήκος 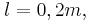 αντίσταση αντίσταση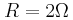 και μπορεί να κινείται χωρίς τριβές πάνω στους και μπορεί να κινείται χωρίς τριβές πάνω στους 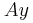 και και 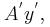 εφαπτόμενη διαρκώς σε αυτούς. Το επίπεδο των εφαπτόμενη διαρκώς σε αυτούς. Το επίπεδο των 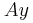 και και 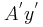 βρίσκεται εντός οριζόντιου ομογενούς μαγνητικού πεδίου έντασης βρίσκεται εντός οριζόντιου ομογενούς μαγνητικού πεδίου έντασης 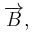 του οποίου οι δυναμικές γραμμές είναι κάθετες σε αυτό. Ο αγωγός ΚΛ ισορροπεί. του οποίου οι δυναμικές γραμμές είναι κάθετες σε αυτό. Ο αγωγός ΚΛ ισορροπεί. Α) Να προσδιορίσετε την ένταση του μαγνητικού πεδίου. Κλείνουμε το διακόπτη Δ. B1) Να προσδιορίσετε την αρχική επιτάχυνση που αποκτά η ράβδος ΚΛ (φορά και μέτρο). B2) Να υπολογίσετε την Η.Ε.Δ. 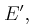 με την οποία θα έπρεπε να αντικαταστήσουμε την συνδεδεμένη πηγή, ώστε η ράβδος ΚΛ να παραμείνει ακίνητη, αν γνωρίζουμε ότι η νέα πηγή έχει εσωτερική αντίσταση με την οποία θα έπρεπε να αντικαταστήσουμε την συνδεδεμένη πηγή, ώστε η ράβδος ΚΛ να παραμείνει ακίνητη, αν γνωρίζουμε ότι η νέα πηγή έχει εσωτερική αντίσταση 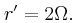 Δίνεται 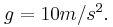 |
 |
A) E = i (r + R) => 12 = i (1 + 2) => i = 4 A
ισορροπία ράβδου ΚΛ : ΣF = 0 => m g - FL = 0 => m g = B i l => 0,1 10 = B 4 0,2 => B = 1,25 T (x)
κλείνουμε τον διακόπτη
B1) R* = R R / (R+R) = R/2 = 2Ω/2 = 1Ω E = i (r + R*) => 12 = i' (1 + 1) => i' = 6 A
VΚΛ = VMN = Vπολική = Ε - i' r = 12 - 6 1 = 6 Volt iΚΛ = Vπολική / R = 6 / 2 = 3 Α
FL = B iΚΛ l = 1,25 T 3 A 0,2 m = 0,75 N ΣF = m g - FL = 1 - 0,75 = 0,25 Ν
α = ΣF / m = 0,25 / 0,1 = 2,5 m/s2 κατακόρυφη προς τα κάτω **
B2) η ΚΛ ισορροπεί όταν διαρρέεται από ρεύμα i = 4 A
VΚΛ = 4 Α 2 Ω = 8 V = VMN = iMN R = iMN 2 => iMN = 4 A οπότε το ολικό ρεύμα είναι Ι = 8 Α
E' = Ι (r' + R*) => Ε' = 8 (2 + 1) = 24 Volt
** E + B l v = i (r + R*) => i = (E + B l v) / (r + R*)
VΚΛ = i R* = i R/2 = (E + B l v) / (r + R*) . R/2
i1 = VΚΛ / R = (E + B l v) / (r + R*) . R/2 / R = (E + B l v) / 2(r + R*)
FL = B i1 l = B l (E + B l v) / 2(r + R*)
FL = 1,25 0,2 (12 + 1,25 0,2 v) / 2(1+ 1) = 0,25 (12 + 0,25 v) / 4 => FL = 3/4 + 1/64 v
ΣF = m a => m g - FL = m a => 0,1 10 - ( 3/4 + 1/64 v ) = 0,1 a => 1/4 - 1/64 v = 0,1 a =>
=> a = 10/4 - 10/64 v => a = 5/2 - 5/32 v ευθεία v = 0 a = 2,5 m/s2 a = 0 v = 16 m/s
γενικά έχουμε :
ΣF = m a => m g - FL = m a => m g - B l (E + B l v) / 2(r + R*) = m dv/dt =>
=> { 2mg(r + R*) - EBl } - B2 l2 v = 2m(r + R*) dv/dt =>
=> v - { 2mg(r + R*) - EBl } / B2 l2 = - 2m(r + R*)/ B2 l2 dv/dt =>
=> dv / [ v - { 2mg(r + R*) - EBl } / B2 l2 ] = - B2l2 / 2m(r + R*) dt =>
=> ln [ v - { 2mg(r + R*) - EBl } / B2 l2 ] / [ - { 2mg(r + R*) - EBl } / B2 l2 ] = - B2l2 / 2m(r + R*) t =>
=> v - { 2mg(r + R*) - EBl } / B2l2 = - { 2mg(r + R*) - EBl } / B2l2 e- (Bl)2 / 2m(r + R*) t =>
=> v(t) = { 2mg(r + R*) - EBl } / B2l2 . [ 1 - e- (Bl)2 / 2m(r + R*) t ]
υ(0) = 0
υ(¥) = { 2mg(r + R*) - EBl } / B2l2 οριακή ταχύτητα = ( 2 0,1 10 2 - 12 5/4 0,2 ) / (1,25 0,2)2 = 16 m/s
a = dv/dt = [ 2mg(r+R*) - EBl ] / 2m(r+R*) . e- (Bl)2 / m(r + R*) t => a(t) = [ g - EBl / 2m(r+R*) ] . e- (Bl)2 / m(r + R*) t
g - EBl / 2m(r + R*) = 10 - 12 5/4 0,2 / 2 0,1 2 = 10 - 3 / 0,4 = 10 - 7,5 = 2,5 m/s2 αρχική επιτάχυνση ράβδου
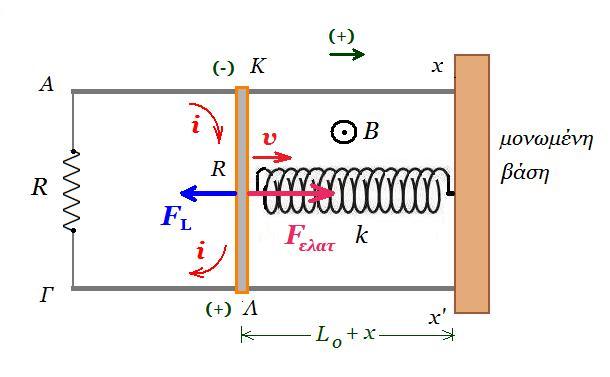
B. Στην διάταξη του σχήματος, ο αγωγός ΚΛ μήκους l ωμικής αντίστασης R και μάζας m αποτελεί τμήμα ενός κλειστού κυκλώματος που δημιουργούν οι οριζόντιοι και παράλληλοι αγωγοί-οδηγοί Αx, Γx' και ο αντιστάτης αντίστασης R.
Οι αγωγοί-οδηγοί Αx, Γx' έχουν αμελητέα αντίσταση και πάνω τους μπορεί να ολισθαίνει ο αγωγός ΚΛ χωρίς τριβές, παραμένοντας διαρκώς κάθετος σε αυτούς. Τα x και x' συνδέονται με ακλόνητη μονωμένη βάση, στο μέσον της οποίας είναι στερεωμένο σε οριζόντιο ιδανικό ελατήριο σταθεράς k του οποίου η άλλη άκρη είναι δεμένη στο μέσον του αγωγού ΚΛ. Η όλη διάταξη βρίσκεται μέσα σε κατακόρυφο ομογενές μαγνητικό πεδίο του οποίου η ένταση έχει μέτρο Β με τις δυναμικές γραμμές να έχουν φορά από τη σελίδα προς τον αναγνώστη. Εκτρέπουμε τον αγωγό ΚΛ παράλληλα στον εαυτό του προς τα αριστερά κατά -Αο και τη χρονική στιγμή t=0s τον αφήνουμε ελεύθερο να κινηθεί. Το είδος της κίνησης του αγωγού είναι
α. φθίνουσα ταλάντωση με την δύναμη αντίστασης να είναι της μορφής F=-bυ.
β. απλή αρμονική ταλάντωση σταθερού πλάτους Αο.
γ. εξαναγκασμένη ταλάντωση με συχνότητα f = Φ(k/m) / 2π
στη ράβδο ΚΛ ασκείται δύναμη Hooke Fελατ = - k x, όπου x<0 η επιμήκυνση του ελατηρίου, με κατεύθυνση οριζόντια προς τα δεξιά οπότε μετατοπίζεται κατά dx σε χρόνο dt μέσα στο ομογενές μαγνητικό πεδίο κινούμενη με ταχύτητα υ = dx / dt προς τα δεξιά, τα ηλεκτρόνιά της δέχονται δύναμη Lorenz και μετακινούνται προς το άκρο Κ που φορτίζεται αρνητικά, οπότε το άκρο Λ φορτίζεται θετικά, ή αλλιώς η ράβδος κόβει δυναμικές γραμμές έτσι έχουμε μεταβολή μαγνητικής ροής σε μια επιφάνεια με εμβαδόν dA = l Χ dx έτσι αναπτύσσεται επαγωγική τάση στα άκρα της ράβδου Εεπαγ = - dΦ/dt = - B dA/dt συν0° = - B l dx/dt = - Β l v συνεπώς το κύκλωμα διαρρέεται με ρεύμα i = |Εεπαγ| / 2R = Β l v / 2R οπότε η ράβδος δέχεται δύναμη Laplace μέτρου FL = B i l = B2 l2 v / 2R με κατεύθυνση οριζόντια προς τα αριστερά
έτσι έχουμε ΣF = Fελατ - FL = - k x - B2 l2 v / 2R = - k x - b v όπου b = B2 l2 / 2R και x < 0 συνεπώς η ράβδος εκτελεί φθίνουσα ταλάντωση με την δύναμη αντίστασης να είναι της μορφής F=-bυ με σταθερά απόσβεσης b = B2 l2 / 2R
αν οι αντιστάσεις του κυκλώματος είναι μικρές η σταθερά απόσβεσης είναι μεγάλη και η περίοδος της ταλάντωσης αυξάνεται ενώ το πλάτος της μειώνεται
αν οι αντιστάσεις του κυκλώματος είναι πολύ μεγάλες η σταθερά απόσβεσης τείνει στο μηδέν και η ράβδος θα κάνει περίπου ΑΑΤ με σταθερά ταλάντωσης D = k
ΑΣΚΗΣΗ 1.
Σωληνοειδές έχει μήκος l = 0,4 m και Ν = 400 σπείρες διαμέτρου Δ = 0,1 m η κάθε μία. Το μεταλλικό σύρμα από το οποίο είναι φτιαγμένο το σωληνοειδές έχει διατομή δ = 0,4 mm και η ειδική του αντίσταση είναι ρ = 1,5 10-8 Ωm. Παράλληλα με το σωληνοειδές συνδέεται αντίσταση R = 7,5 Ω και το σύστημα τροφοδοτείται με ηλεκτρική πηγή συνεχούς με ΗΕΔ Ε = 18 V και εσωτερική αντίσταση r = 1 Ω. Να υπολογίσετε :
(α) την ωμική αντίσταση του σωληνοειδούς
(β) την ένταση του ρεύματος που διαρρέει την πηγή
(γ) την ένταση του μαγνητικού πεδίου στο εσωτερικό
(δ) τον ρυθμό με τον οποίο η ηλεκτρική ενέργεια της πηγής μετατρέπεται σε θερμότητα στο σωληνοειδές.
l = N δ = 400 0,4 10-3 = 0,16 m μήκος πηνίου
Α = π Δ2 / 4 = π 0,12 / 4 = 25π 10-4 m2 εμβαδόν κάθε σπείρας πηνίου
S = π δ2 / 4 = π (0,4 10-3)2 / 4 = 4π 10-8 m2 εμβαδόν διατομής κάθε σπείρας πηνίου
λ = Ν 2π Δ/2 = 400 π 0,1 = 40π m μήκος σύρματος πηνίου
Rπην = ρ λ / S = 1,5 10-8 40π / 4π 10-8 = 15 Ω ωμική αντίστασης πηνίου
Rολ = r + R Rπην / (Rπην + R) = 1 + 7,5 15 / 22,5 = 1 + 5 = 6 Ω συνολική αντίσταση
i = E / Rολ = 18 V / 6 Ω = 3 A
Vπην = E - i r = 18V - 3A 1Ω = 15 V
iπην = Vπην / Rπην = 15V / 15Ω = 1 A
B = 4π 10-7 Ν i / l = 4π 10-7 400 1 / 0,4 = 4π 10-4 T
Pπην = iπην2 Rπην = 1 15 = 15 J/s = 15 Watt
ΑΣΚΗΣΗ 2.
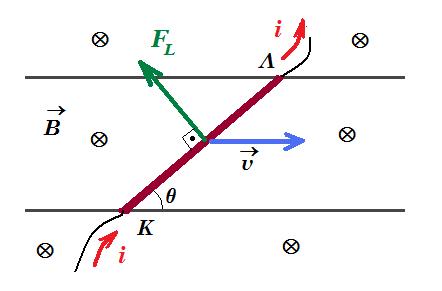
Ευθύγραμμος αγωγός μήκους l = 1 m μπορεί να ολισθαίνει πάνω σε οριζόντιες παράλληλες σιδηροτροχιές αμελητέας ωμικής αντίστασης έτσι ώστε τα άκρα του να εφάπτονται συνέχεια στις σιδηροτροχιές και να σχηματίζει με αυτές γωνία θ = 30°.  Το σύστημα βρίσκεται σε κατακόρυφο ομογενές μαγνητικό πεδίο εντάσεως Β = 0,1 Τ. Αν ο αγωγός διαρρέεται από ρεύμα Ι = 10 Α και ολισθαίνει με σταθερή ταχύτητα μέτρου υ = 5 m/s να υπολογίσετε :
Το σύστημα βρίσκεται σε κατακόρυφο ομογενές μαγνητικό πεδίο εντάσεως Β = 0,1 Τ. Αν ο αγωγός διαρρέεται από ρεύμα Ι = 10 Α και ολισθαίνει με σταθερή ταχύτητα μέτρου υ = 5 m/s να υπολογίσετε :
(α) το μέτρο της δύναμης που πρέπει να ασκούμε στον αγωγό ΚΛ ώστε να κινείται με σταθερή ταχύτητα
(β) την ισχύ της δύναμης Laplace.
v = σταθερή ΣF = 0 => F - FL = 0 => F = B I l = 0,1 T 10 A 1 m = 1 N
dWFL = FL dx συν(90° + 30°) => PFL = dWFL / dt = FL dx/dt συν(90° + 30°) = FL v συν(90° + 30°) = 1 N 5 m/s (-1/2) = - 2,5 J/s
ΘΕΜΑ 1.
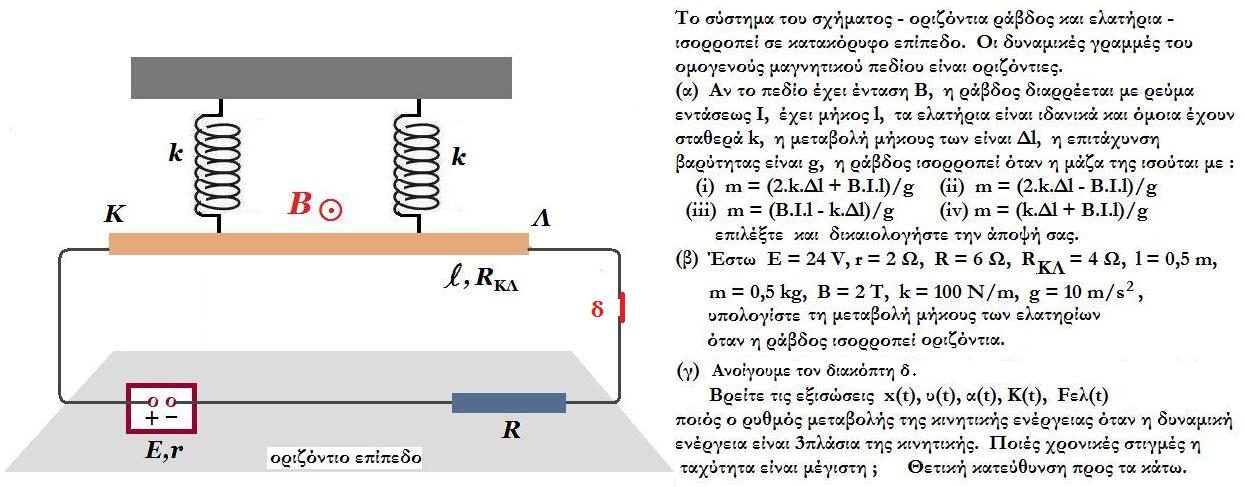
(α) ισορροπία ράβδου : m.g + B.i.l = 2.k.Δl => m = ( 2.k.Δl - B.i.l ) / g όπου Δl : επιμήκυνση ελατηρίου
(β) νόμος Ohm για κλειστό κύκλωμα : Ε = i . (RΚΛ + R + r) => 24 V = i . (4 Ω + 6 Ω + 2 Ω) => i = 2 Α
από τη σχέση ισορροπίας της ράβδου έχουμε : m.g + B.i.l = 2.k.Δl => ( m.g + B.i.l ) / 2.k = Δl =>
=> Δl = ( 0,5 kg . 10 m/s2 + 2 T . 2 A . 0,5 m ) / 2.100 N/m => Δl = 0,035 m = 3,5 cm
(γ) όταν ανοίξουμε τον διακόπτη δ, στη ράβδο ασκούνται : το βάρος της και οι δυνάμεις από τα ελατήρια που είναι επιμηκυμένα κατά Δl = 0,035 m
θέση ισορροπίας ράβδου : m.g = 2.k.x0 => x0 = m.g/2.k = 0,5 . 10 / 2.100 => x0 = 0,025 m = 2,5 cm επιμήκυνση
η ράβδος θα κάνει ΑΑΤ με πλάτος (3,5 - 2,5) cm = 1 cm = 0,01 m και αρχική φάση + π/2 rad
η θετική κατεύθυνση είναι προς τα κάτω και η ράβδος βρίσκεται κάτω από τη θέση ισορροπίας της με τα ελατήρια
D = 2.k = m. ω2 => 2.k / m = ω2 => ω = (2.100/0,5)½ => ω = 20 rad/s Τ = 2π/ω = 2π/20 = π/10 sec
x(t) = Α.ημ(ωt + φ) => x(t) = 0,01 ημ(20t + π/2) υ(t) = 0,2 συν(20t + π/2) α(t) = -4 ημ(20t + π/2)
K(t) = ½ . m . υ2 = ½ . 0,5 . 0,22 συν2(20t + π/2) =>
=> K(t) = 0,01 συν2(20t + π/2) = 0,005 + 0,005 συν(40t + π) = 0,005 - 0,005 συν40t
ΣF = m.a => m.g + 2.Fελατ = m.a =>
=> Fελατ(t) = ½ .( m.a - m.g ) = ½ . 0,5 . [ -4 ημ(20t + π/2) - 10 ] =>
Fελατ(t) = - 2,5 - ημ(20t + π/2) = - 2,5 - συν20t
Fελατ(0) = - 2,5 - ημ (π/2) = - 3,5 N = - 100 Ν/m . 0,035 m = k . Δl για κάθε ελατήριο
Fελατ(t)max = - 2,5 - 1 = - 3,5 N Fελατ(t)min = - 2,5 + 1 = - 1,5 N
U = 3.K => U = 3/4 . E => ½.D.x2 = 3/4 . ½.D.A2 => x = ± Α 3½ /2 => ημ(20t + π/2) = ±3½/2 =>
συν(20t + π/2) = ±1/2 τότε x = 0,01 . (± 3½/2 ) = ± 0,005 3½ m απομάκρυνση
α = ± 2 3½ m/s2 επιτάχυνση, υ = 0,2 . (±1/2 ) = ± 0,1 m/s ταχύτητα
ρυθμός μεταβολής κινητικής ενέργειας : |dK/dt| = m . υ . α = 0,5 . 0,1.3½ . 2 = 0,1 .3½ J/s
η ταχύτητα γίνεται μέγιστη όταν : συν(20t + π/2) = ±1 => 20t + π/2 = Ν.π => t = Ν.π/20 - π/40 Ν = 1, 2, 3, ...
ΘΕΜΑ 2.
Ένα σωληνοειδές με Ν = 1000 σπείρες και μήκος l = 1 m έχει αντίσταση R = 8 Ω. Συνδέουμε το σωληνοειδές σε σειρά με λαμπτήρα που έχει στοιχεία κανονικής λειτουργίας 12 V, 48 W και στα άκρα της συνδεσμολογίας συνδέουμε ηλεκτρική πηγή με ΗΕΔ Ε = 48 V και εσωτερική αντίσταση r. Ο λαμτήρας λειτουργεί κανονικά. (α) Υπολογίσε την ένταση του μαγνητικού πεδίου στο κέντρο του σωληνοειδούς.
Κόβουμε το σωληνοειδές στη μέση και τοποθετούμε το ένα κομμάτι στη θέση του αρχικού. (β) Πόση είναι η ένταση του μαγνητικού πεδίου στο κέντρο του νέου σωληνοειδούς; (γ) Ο λαμπτήρας λειτουργεί κανονικά;
P = V . i => i = P / V = 48 W / 12 V => i = 4 A Rλ = V / i = 12 V / 4 A => Rλ = 3 Ω
E = i . ( r + R + Rλ ) => 48 = 4 . ( r + 8 + 3 ) => r = 1 Ω
Β = 4π 10-7 Ν i / l => B = 4π 10-7 1000 4 / 1 => B = 16π 10-4 Tesla
E = i . ( r + R + Rλ ) => 48 = i . ( 1 + 4 + 3 ) => i = 6 A
Β' = 4π 10-7 Ν i / l => B = 4π 10-7 500 6 / 0,5 => B = 24π 10-4 Tesla
ο λαμπτήρας διαρρέεται με ρεύμα 6 Α άρα υπερλειτουργεί P' = i2 Rλ = 62 3 = 108 W > 48 W
ΘΕΜΑ 3.
Σωληνοειδές με Ν = 500 σπείρες και μήκος l = 1 m έχει αντίσταση R1 = 3 Ω. Συνδέουμε το σωληνοειδές σε σειρά με αντιστάτη που έχει αντίσταση R2 = 2 Ω και στα άκρα της συνδεσμολογίας συνδέουμε ηλεκτρική πηγή με ΗΕΔ Ε και εσωτερική αντίσταση r = 1 Ω. Η ένταση του μαγνητικού πεδίου στο κέντρο του σωληνοειδούς είναι B = π 10-3 Tesla. (α) Υπολογίστε την ΗΕΔ της πηγής και σχεδιάστε τη συμβατική φορά του ρεύματος.
Συνδέουμε άλλον αντιστάτη με αντίσταση R3 = 6 Ω παράλληλα στο σωηνοειδές.
(β) Υπολογίστε την ένταση του μαγνητικού πεδίου στο κέντρο του σωληνοειδούς.
(γ) Υπολογίστε την θερμική ισχύ που αναπτύσσεται στο σωληνοειδές.
(δ) Τοποθετούμε σιδηροπυρήνα στο εσωτερικό του σωληνοειδούς μ = 5000. Υπολογίστε την ένταση του μαγνητικού πεδίου

Β = 4π 10-7 Ν i / l => π 10-3 = 4π 10-7 500 i / 1 => i = 5 Α
E = i . ( r + R1 + R2 ) => Ε = 5 . ( 1 + 3 + 2 ) => Ε = 30 V
R1,3 = R1 R3 / ( R1 + R3 ) = 3 6 / ( 3 + 6 ) = 2 Ω
E = i . ( r + R2 + R1,3 ) => 30 = i . ( 1 + 2 + 2 ) => i = 6 A
Vπην = i . R1,3 = 6 . 2 = 12 V iπην = Vπην / R1 = 12 / 3 = 4 Α
Β' = 4π 10-7 Ν i / l => B' = 4π 10-7 500 4 / 1 => B' = 8π 10-4 Tesla
P = iπην2 R1 = 42 3 = 48 W
B'' = 5000 . 8π 10-4 Tesla = 4π Τ
ΘΕΜΑ 4.

έχουμε και λέμε

ΘΕΜΑ 5.
Οι κατακόρυφοι μεταλλικοί αγωγοί Αy και Γy' έχουν μεγάλο μήκος αμελητέα ωμική αντίσταση και απέχουν απόσταση l = 1 m και η βάση στήριξης τους στο έδαφος είναι ηλεκτρικά μονωμένη. Ο αγωγός ΚΛ μήκους l = 1 m μάζας m = 200 g και ωμικής αντίστασης RΚΛ = 0,4 Ω έχει τα άκρα του Κ και Λ σε ηλεκτρική επαφή με τους αγωγούς Αy και Γy' και απέχει κατακόρυφη απόσταση Η= 6 m από το έδαφος. Η όλη διάταξη βρίσκεται μέσα σε ομογενές μαγνητικό πεδίο έντασης Β = 0,5 Τ κάθετο στο επίπεδο των αγωγών. Τα άκρα Α και Γ συνδέονται με αντιστάτη ωμικής αντίστασης R = 0,1 Ω. Κάποια στιγμή εκτοξεύουμε τον αγωγό ΚΛ με κατακόρυφη ταχύτητ μέτρου υo = 1 m/s με φορά προς τα κάτω. Στην κίνηση του αγωγού αντιτίθεται συνολική δύναμη τριβής μέτρου Τ = 1 Ν λόγω της επαφής με τους κατακόρυφους αγωγούς. Ο αγωγός ΚΛ αφού διανύσει κατακόρυφη απόσταση d = 4 m εξέρχεται του μαγνητικό πεδίο έχοντας αποκτήσει οριακή ταχύτητα.
Δ1. Υπολογίστε την κινητική ενέργεια του αγωγού ΚΛ όταν εξέρχεται από το μαγνητικό πεδίο.
Δ2. Υπολογίστε τον ρυθμό μεταβολής της κινητικής ενέργειας του αγωγού ΚΛ όταν η τάση στα άκρα του είναι 0,15 V.
Δ3. Εκφράστε την επιτάχυνση του αγωγού συναρτήσει της ταχύτητάς του κατά τη διάρκεια της κίνησής του μέσα στο μαγνητικό πεδίο.
Δ4. Βρείτε τον λόγο QR / QT της συνολικής θερμότητας που εκλύεται λόγω φαινομένου Joule στους αντιστάτες προς τη συνολική θερμότητα που εκλύεται λόγω τριβής μέχρι να φθάσει ο αγωγός στο έδαφος.
Καθ'όλη τη διάρκεια της κίνησης ο αγωγός παραμένει οριζόντιος, οι αντιστάσεις του αέρα αμελητέες.
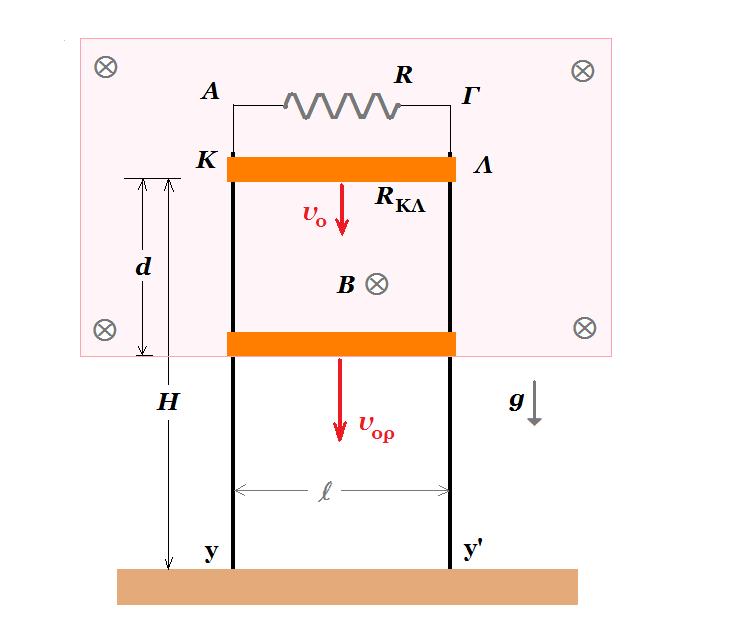
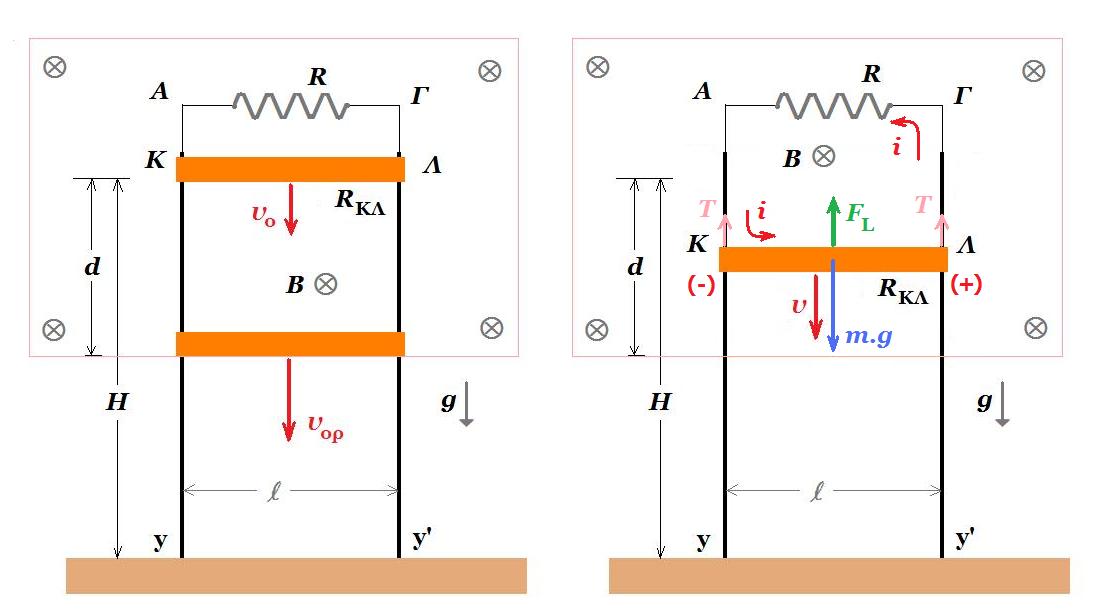
Eεπαγ = Β . υ . l = i . ( R + RΚΛ ) => i = Β . υ . l / ( R + RΚΛ )
FL = B . i . l => FL = B2 . l2 . v / ( R + RΚΛ )
ΣF = m . a => m.g - T - FL = m.a => m.g - T - B2.l2. vορ / (R + RΚΛ) = 0 =>
=> vορ = (m.g - T).(R + RΚΛ) / B2.l2 => vορ = (0,2 . 10 - 1).0,5 / 0,52.12 => vορ = 2 m/s
Kεξόδου = ½ . m . voρ 2 = ½ . 0,2 . 22 = 0,4 J
VΛΚ = i . R => 0,15 V = i . 0,1 Ω => i = 1,5 A FL = B . i . l = 0,5 . 1,5 . 1 = 3/4 N
m.g - T - FL = m.a => 2 - 1 - 0,75 = 0,2.a => 0,25 = 0,2.a => a = 1,25 m/s2
i = Β . υ . l / ( R + RΚΛ ) => 1,5 = 0,5 . υ . 1 / 0,5 => v = 1,5 m/s
dK / dt = m . a . v = 0,2 . 1,25 . 1,5 => dK/dt = 0,375 J/s
ΣF = m . a => m.g - T - FL = m.a => m.g - T - B2.l2. v / (R + RΚΛ) = m.a =>
=> 2 - 1 - 0,25. v / 0,5 = 0,2.a => 5 - 2,5. v = a
QT = T . H = 1 N . 6 m => QT = 6 J
QR = WFL = ½ . m . vo 2 + m . g . d - Τ . d - ½ . m . voρ 2 =
= ½ . 0,2 .12 + 0,2.10.4 - 1.4 - ½ . 0,2 .22 = 0,1 + 8 - 4 - 0,4 => QR = WFL = 3,7 J

ΘΕΜΑ 6.
Ισοπαχής οριζόντια ομογενής δοκός ΑΓ μήκους l = 1 m και μάζας Μ = 2 kg αρθρώνεται στο άκρο της Α σε κατακόρυφο τοίχο. Η δοκός ισορροπεί οριζόντια μέσω αβαρούς , μη εκτατού νήματος το οποίο συνδέεται με το μέσον της Δ ενώ η άλλη άκρη του καταλήγει στον κατακόρυφο τοίχο. Στο άλλο άκρο Γ της δοκού έχει στερεωθεί το επάνω άκρο κατακόρυφου ιδανικού ελατηρίου σταθεράς k = 50 N/m ενώ στο άλλο άκρο έχει δεθεί σφαίρα Σ1 μάζας m1 = 0,5 kg. Mέσω αβαρούς , μη εκτατού νήματος η σφαίρα Σ1 συνδέεται με το μέσο αγώγιμης ομογενούς ράβδου ΚΛ μάζας m2 = 1,5 kg μήκους l = 2 m και ωμικής αντίστασης RΚΛ = 3 Ω. Η ράβδος ΚΛ βρίσκεται σε επαφή με λεία κατακόρυφα σύρματα ΣΣ1 και Σ'Σ2 μεγάλου μήκους αμελητέας ωμικής αντίστασης τα οποία απέχουν σταθερή απόσταση l=2m. Τα κάτω άκρα Σ1 και Σ2 των δύο συρμάτων συνδέονται με αντίσταση R = 1 Ω. Ένα μέρος της διάταξης των συρμάτων ΣΣ1 και Σ'Σ2 βρίσκεται μέσα σε οριζόντιο ομογενές μαγνητικό πεδίο έντασης Β = 2 Τ με δυναμικές γραμμές κάθετες στο επίπεδο κινήσεως της ράβδου.
Κάποια στιγμή κόβουμε το νήμα που συνδέει τη σφαίρα με τη ράβδο. Η σφαίρα εκτελεί απλή αρμονική ταλάντωση με σταθερά επαναφοράς D = k ενώ η ράβδος κινείται κατακόρυφα κατερχόμενη σε επαφή πάντα με τα σύρματα ΣΣ1 και Σ'Σ2 .
Δ1. Να βρεθεί η απόσταση μεταξύ των δύο θέσεων της ταλάντωσης της σφαίρας Σ1 για τις οποίες ισχύει ότι η κινητική ενέργεια είναι τριπλάσια της δυναμικής ενέργειας της ταλάντωσης.
Δ2. Εκφράστε την δύναμη από το ελατήριο συναρτήσει του χρόνου.
Δ3. Υπολογίστε την δύναμη που ασκεί η άρθρωση στη δοκό όταν η σφαίρας Σ1 βρεθεί στο ανώτερο σημείο της τροχιάς της.
Τη στιγμή που η ταχύτητα της σφαίρας Σ1 μηδενίζεται για δεύτερη φορά μετά το κόψιμο του νήματος, η ράβδος ΚΛ εισέρχεται στο χώρο του μαγνητικού πεδίου.
Δ4. Υπολογίστε την Εεπαγ που αναπτύσσεται στα άκρα της ΚΛ, την επιτάχυνση της ράβδου και τον ρυθμό μεταβολής της δύναμης Laplace.
Δ5. Υπολογίστε την οριακή ταχύτητα της ράβδου και βρείτε μαθηματική σχέση της επιτάχυνσης α σε σχέση με την ταχύτητα υ.
Θεωρούμε χρονική στιγμή t0 = 0 τη στιγμή που η ράβδος αποκτά οριακή ταχύτητα. Τότε απέχει από τη βάση Σ1Σ2 απόσταση h = 10 m.
Δ6. Μετά από χρονική διάρκεια Δt από την στιγμή t0 το ηλεκτρικό φορτίο που διέρχεται από μια διατομή της ράβδου ΚΛ έχει τιμή q = 7,5 C. Υπολογίστε πόσο απέχει η ράβδος από τη βάση Σ1Σ2 και να γράψετε την εξίσωση του μέτρου της μαγνητικής ροής που διέρχεται από το κλειστό κύκλωμα συναρτήσει του χρόνου για την παραπάνω χρονική διάρκεια.
Οι αντιστάσεις αέρα αμελητέες.
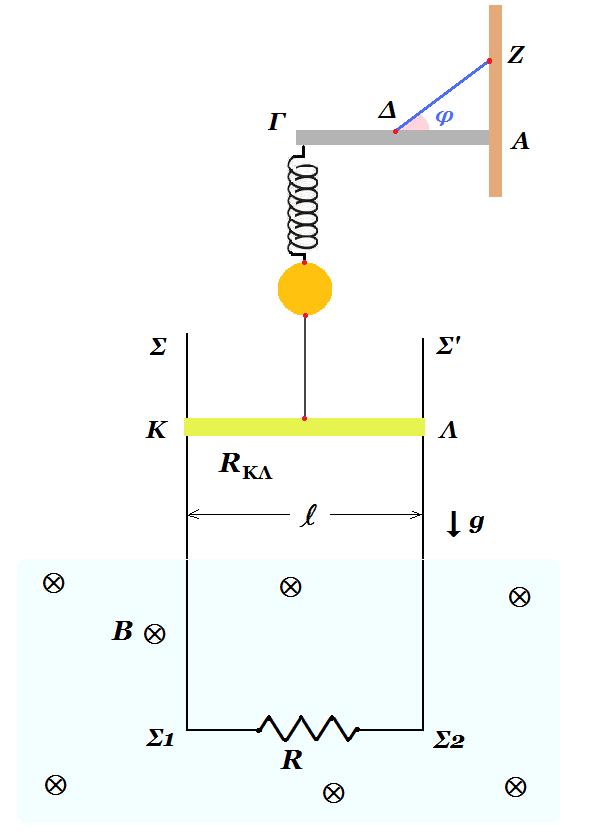
Δ1.
ισορροπία δοκού ΑΓ : ΣFx = TΔ(x) - FA(x) = 0 (1)
ΣFy = M.g + Fελατ - TΔ(y) + FA(y) = 0 (2)
ροπές ως προς Δ : Fελατ .(ΓΔ) - FA(y) .(ΔΑ) = 0 => Fελατ = FA(y) (3) (ΓΔ) = (ΔΑ) = (ΑΓ)/2
ροπές ως προς Α : Fελατ .(ΑΓ) + M.g .(ΔΑ) - TΔ(y) .(ΔΑ) = 0 => 2.Fελατ + M.g - TΔ(y) = 0 (4)
ισορροπία σφαίρας : m1.g - Fελατ + T = 0 (5)
ισορροπία ράβδου ΚΛ : m2.g - T = 0 => Τ = 15 Ν
(5) => Fελατ = 5 + 15 => Fελατ = 20 Ν k.Δl = Fελατ => Δl = 20/50 => Δl = 0,4 m
(4) => TΔ(y) = 2.20 + 20 => TΔ(y) = 60 Ν
(3) => FA(y) = 20 Ν
Δ2.
τη στιγμή που κόβουμε το νήμα το ελατήριο είναι επιμηκυμένο κατά Δl = 0,4 m
ισορροπία σφαίρας : m1.g = Fελατ = k.x1 => x1 = 5/50 = 0,1 m άρα A = Δl - x1 = 0,3 m
ω2 = k / m1 = 50 / 0,5 => ω = 10 rad/s Τ = 2π/ω = π/5 s
x(t) = 0,3 ημ(10.t + π/2) v(t) = 3 συν(10.t + π/2) α(t) = -30 ημ(10.t + π/2)
ΣF = m1 . a => m1.g + Fελατ = m1 . a => Fελατ = m1 .a - m1.g =>
=> Fελατ (t) = -15 ημ10.t - 5 = - k.x(t) - 5
Κ = 3.U => U = E/4 => x = ± A/2 = ± 0,15 m
η απόσταση της θέσης x = - 0,15 m από τη θέση x = + 0,15 m είναι 0,3 m
Δ3.
τη στιγμή που η σφαίρα είναι στο ανώτατο σημείο της τροχιάς της το ελατήριο είναι συσπειρωμένο κατά 0,2 m
x = - 0,3 m => Fελατ = - k.x - 5 = - 50 . (-3) - 5 = 15 - 5 = +10 N η δοκός δέχεται δύναμη από το ελατήριο - 10 Ν (προς τα πάνω)
(3) => FA(y) = Fελατ = 10 Ν (προς τα πάνω)
(4) => 2.Fελατ + M.g - TΔ(y) = 0 => 2.(-10) + 20 - TΔ(y) = 0 => TΔ(y) = Τ ημφ = 0 άρα Τ = 0
(1) => FA(x) = TΔ(x) = Τ συνφ = 0
συνεπώς η δοκός στην άρθρωση Α δέχεται δύναμη FA(y) = Fελατ = 10 Ν (προς τα πάνω)
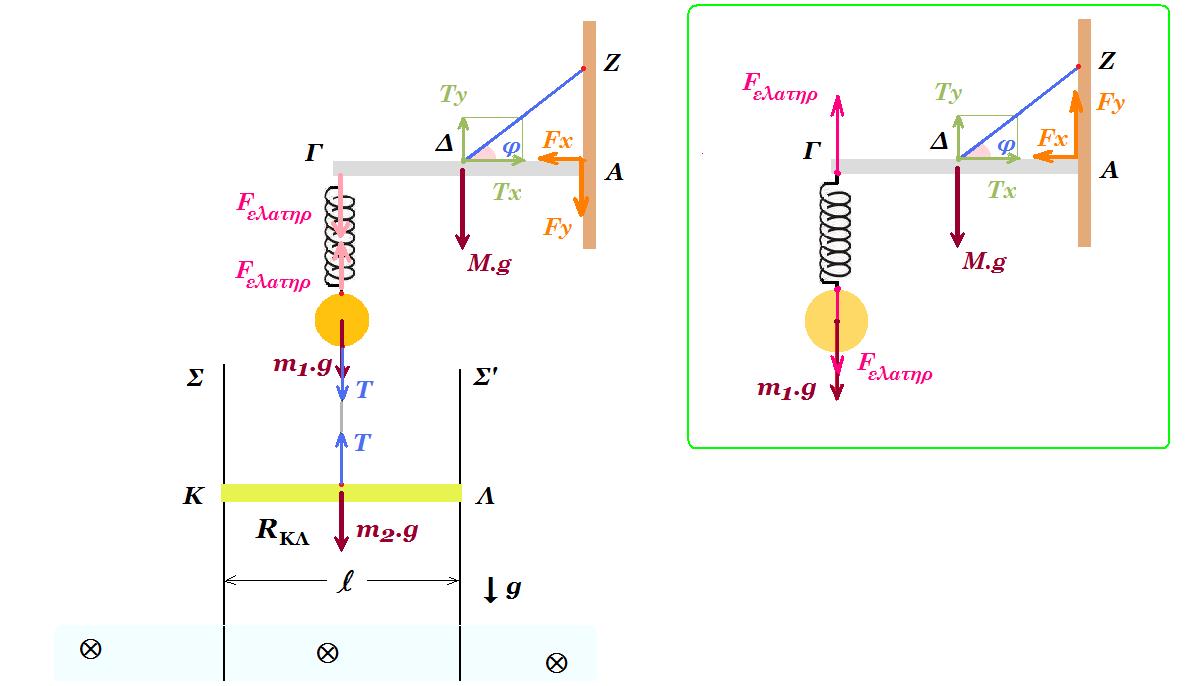
Δ4.
v(t) = 3 συν(10t + π/2) = 0 => συν(10t + π/2) = 0 = συν(π/2) => 10t + π/2 = Νπ + π/2 Ν=1,2,3,...
Ν = 1 : t = π/10 s , Ν = 2 : t = π/5 s = Τ , Ν = 3 : t = 3π/10 s , ...
η ράβδος κάνει ελεύθερη πτώση : υ = g . t, y = ½ . g . t2
υ = g . t = 10 . π/5 => v = 2π m/s Eεπαγ = Β . υ . l = 2 . 2π . 2 => Eεπαγ = 8π Volt
y = ½ . g . t2 = ½ . 10 . (π/5)2 = 5 . 10 / 25 => y = 2 m η ράβδος σε χρόνο π/5 s έχει διανύσει 2 m και έχει αποκτήσει ταχύτητα 2π m/s
Eεπαγ = Β . υ . l = i .( R + RΚΛ ) => i = 8π / (1 + 3) => i = 2π A
FL = B . i . l => FL = 2 . 2π . 2 => FL = 8π Ν
ΣF = m2 . a => m2 .g - FL = m2 .a => 15 - 8π = 1,5 . a => a = 10 - 16π/3 m/s2 < 0 επιβράδυνση
dFL / dt = FL . v . συνπ = 8π Ν . 2π m/s . (-1) = - 16π2 = - 160 => dFL / dt = - 160 J/s τα διανύσματα FL και v είναι αντίρροπα
Δ5.
Eεπαγ = Β . υ . l = i . ( R + RΚΛ ) => i = Β . υ . l / ( R + RΚΛ )
FL = B . i . l => FL = B2 . l2 . v / ( R + RΚΛ )
ΣF = m2 . a => m2 .g - FL = m2 .a => m2 .g - B2.l2. vορ / (R + RΚΛ) = 0 =>
=> vορ = m2 .g.(R + RΚΛ) / B2.l2 => vορ = 1,5 . 10 . 4 / 22.22 => vορ = 15/4 m/s επειδή αρχικά FL = 8π Ν > m.g = 15 Ν η ράβδος ΚΛ θα κινηθεί επιβραδυνόμενα μέχρι α = 0 επειδή συν τω χρόνω αυξάνεται η ταχύτητά της, οπότε θα αποκτήσει οριακή ταχύτητα
m2 .g - FL = m2 .a => m2 .g - B2.l2.v/(R + RΚΛ) = m2 .a => 15 - 22.22.v/(1 + 3) = 1,5.a => a = 10 - 8/3.v
υ = 2π α = 10 - 16π/3 υ = 15/4 α = 10 - 8/3 . 15/4 = 10 - 10 = 0
.............................................................................................................................................................................
μελέτη α(v) a(t) v(t) x(t)
a = 10 - 8/3.v => dv/dt = -8/3.(v - 30/8) => dv/dt = -8/3.(v - 15/4) => dv/(v-15/4) = -8/3.dt =>
=> ln { (v - 15/4) / (2π - 15/4) } = -8/3.t => (v - 15/4) / (2π - 15/4) = e-8/3.t => => (v - 15/4) = (2π - 15/4).e-8/3.t => v(t) = 15/4 + (2π - 15/4).e-8/3.t
τ = 3/8 s 5τ = 15/8 s e0 = 1 e-8/3.15/8 = e-5 = 0,0067
v(0) = 15/4 + (2π - 15/4).e-8/3.0 = 15/4 + 2π - 15/4 = 2π m/s αρχική τιμή
v(15/8) = 15/4 + (2π - 15/4).e-5 = 15/4 + (2π - 15/4).0,0067 = 15/4 - 0,017 = 15/4 m/s = υορ
a(t) = dv(t) / dt = -8/3. (2π - 15/4).e-8/3.t
α(0) = -8/3.(2π - 15/4).e-8/3.0 = -8/3.(2π - 15/4) . 1 = -16π/3 + 10 m/s2 αρχική τιμή
α(15/8) = -8/3.(2π - 15/4).e-5 = -8/3.(2π - 15/4).0,0067 = -8/3 . 0,017 = 0,045 m/s2 = 0
dx = v . dt => dx = [ 15/4 + (2π - 15/4).e-8/3.t ] dt =>
=> x = 15/4.t - 3/8.(2π - 15/4). { e-8/3.t - e0 } =>
x(t) = 15/4.t - 3/8.(2π - 15/4). { e-8/3.t - 1 } x(0) = 0
x(15/8) = 15/4. 15/8 - 3/8.(2π - 15/4). { e-8/3.15/8 - 1 } = 7 - 3/8.(2π - 15/4). { 0,0067 - 1 } =
= 7 - 3/8 . 2,53 . (-1) = 7 + 0,95 = 8 m
η ράβδος εισέρχεται στο μαγνητικό πεδίο με ταχύτητα 2π m/s δέχεται δύναμη Laplace και επιβραδύνεται αρχικά με (10 -16π/3) m/s2 αργότερα εξέρχεται από το μαγνητικό πεδίο με ταχύτητα 15/4 m/s = υορ έχοντας επιτάχυνση α = 0 ενώ διάνυσε κατακόρυφη απόσταση 8 m.
...............................................................................................................................
Δ6.
q = ΔΦ / (R + RΚΛ) => ΔΦ = 7,5 C . 4 Ω => ΔΦ = 30 Wb
ΔΦ = B . l . h => h = 30 Wb / (2 T . 2 m) => h = 7,5 m διανυθέν διάστημα από τη ράβδο
Φ = Εεπαγ . t = B . vορ . l . t = 2 . 15/4 . 2 . t => Φ(t) = 15.t
όταν Φ = 30 Wb τότε t = 30 / 15 = 2 s
y = vορ . t = 15/4 . 2 = 7,5 m
άρα η ράβδος απέχει από τη βάση Σ1Σ2 απόσταση : 10 m - 7,5 m = 2,5 m
τη στιγμή t0 = 0 η ράβδος βρίσκεται σε ύψος Η = 10 m τότε η μαγνητική ροή που διέρχεται από το κύκλωμα είναι : Φ0 = Β . Η . l = 2 Τ . 10 m . 2 m = 40 Wb
καθώς κατέρχεται η ράβδος μειώνεται η ροή με ρυθμό 15 Wb/s συνεπώς η εξίσωση της ροής ως προς τον χρόνο θα είναι : Φ(t) = 40 - 15.t t ε [0, 2 s]
ΘΕΜΑ 7.
Τα άκρα Γ και Δ δύο παράλληλων οριζοντίων αγωγών Γx και Δx' αμελητέας ωμικής αντίστασης συνδέονται με αγωγό αντίστασης R1 = 0,4 Ω. Επάνω στυς δύο αγωγούς είναι τοποθετημένος κάθετα προς την διεύθυνσή τους άλλος ευθύγραμμος αγωγός ΚΛ με μήκος l=1m , μάζας m=0,5kg , ωμικής αντίστασης R2 = 0,1 Ω ο οποίος μπορεί να ολισθαίνει χωρίς τριβές. Η όλη διάταξη βρίσκεται μέσα σε ομογενές μαγνητικό πεδίο έντασης Β = 1 Τ με δυναμικές γραμμές κάθετες στο επίπεδο των αγωγών. Ο αγωγός ΚΛ κινείται με σταθερή ταχύτητα μέτρου υ0 = 2m/s με τον διακόπτη δ ανοικτό. Τη στιγμή t = 0 κλείνει ο διακόπτης δ χωρίς να δημιουργηθεί σπινθήρας και ασκείται στον αγωγό ΚΛ εξωτερική δύναμη F έτσι ώστε ο αγωγός επιταχύνεται με επιτάχυνση α = 1 m/s 2.
Γ1. Γράψτε τη χρονική εξίσωση της δύναμης F.
Γ2. Βρείτε το επαγωγικό φορτίο που διέρχεται από μια διατομή του αγωγού ΚΛ από τη στιγμή 1 s έως τη στιγμή 3 s.
Τη στιγμή t1 = 3 s καταργείται η δύναμη F και ο αγωγός ΚΛ επιβραδύνεται μέχρι να μηδενισθεί η ταχύτητά του.
Γ3. Υπολογίστε τον ρυθμό μεταβολής της ορμής του ΚΛ τη στιγμή που η ταχύτητά του ισούται με το μισό της μέγιστης τιμής της μετά την κατάργηση της δύναμης F.
Γ4. Βρείτε τη θερμότητα που εκλύεται από το κύκλωμα κατά τη διάρκεια της επιβραδυνόμενης κίνησης.
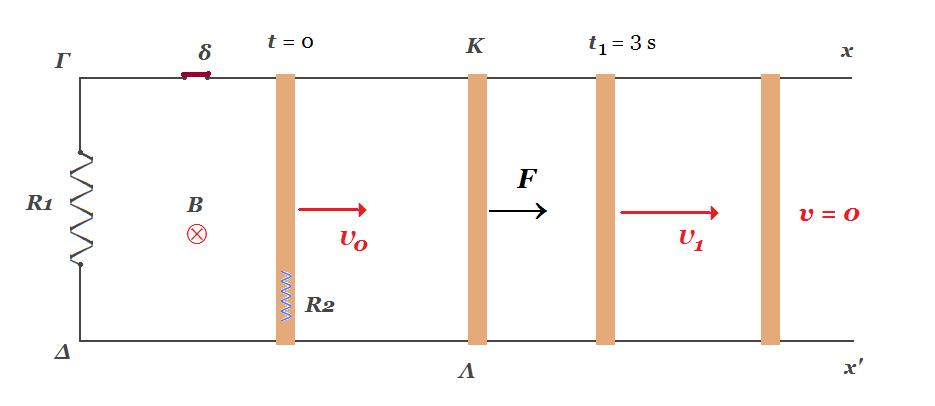
Γ1. Eεπαγ = Β υ0 l = 1 T . 2 m/s . 1 m = 2 Volt αρχική επαγωγική τάση στον αγωγό ΚΛ
αργότερα ο αγωγός έχει ταχύτητα υ και το κύκλωμα διαρρέεται με ρεύμα εντάσεως :
i = Eεπαγ / (R1 + R2) = Β υ l / (R1 + R2)
FL = B i l = Β2 l2 υ / (R1 + R2) = 1 1 υ / 0,5 => FL = 2υ
ΣF = m a => F - FL = m a => F = 2υ + 0,5 1 => F = 0,5 + 2υ
ταχύτητα αγωγού : υ = υ0 + α t = 2 + t οπότε F = 0,5 + 2 ( 2 + t ) => F(t) = 4,5 + 2t
Γ2. i = Β l υ / (R1 + R2) = 1 1 (2 + t) / 0,5 = 2 (2 + t) => i(t) = 2t + 4
i(1) = 2 + 4 = 6 A i(3) = 2 3 + 4 = 10 A q = (3 - 1) [ i(1) + i(3) ] / 2 = 2 (6 + 10) / 2 = 16 C
Γ3. υ = υ0 + α t = 2 + t = v(t) v(3) = 2 + 3 = 5 m/s
ΣF = m a => - FL = m a => - Β2 l2 υ / (R1 + R2) = m a => - 1 1 υ / 0,5 = 0,5 a => - 4υ = a =>
=> - 4 v = dv/dt => dv/v = - 4 dt => [ ln v ]5®u = - 4 t => lnv - ln5 = - 4t =>
=> ln (v/5) = - 4t => v = 5 e-4t = v(t) ταχύτητα a = dv/dt = - 20 e-4t = a(t) επιτάχυνση
η ταχύτητα μειώνεται εκθετικά με τον χρόνο το ( - ) στην α(t) σημαίνει επιβράδυνση
όταν υ = υ(3) / 2 = 5/2 = 2,5 m/s τότε - υ = 0,25 a => α = - 4 2,5 = - 10 m/s2
ρυθμός μεταβολής ορμής : Δp / Δt = ΣF = m a = 0,5 kg ( - 10 m/s2 ) = - 5 N
Γ4. Qθερμ = ΔΚ = Κτελ - Καρχ = 0 - ½ m υ(3)2 = ½ 0,5 52 = 25/4 Joule
v = 5 e-4t = v(t) = dx/dt => dx = 5 e-4t dt => x(t) = -5/4 ( e-4t - 1 ) x(0) = 0
τ = 1/4 s , 5τ = 5/4 s , e-4 5/4 = e-5= 0,006738
x(5τ) = x(5/4) = - 5/4 ( 0,006738 - 1 ) = 5/4 m
v(5τ) = v(5/4) = 5 0,006738 = 0
a(5τ) = a(5/4) = - 20 0,006738 = 0
σε χρόνο 5τ = 5/4 s ο αγωγός ΚΛ έχει διανύσει απόσταση 5/4 = 1,25 m και σταματά
ΘΕΜΑ 8.
Οι κατακόρυφοι μεταλλικοί αγωγοί Αy και Γy' έχουν μεγάλο μήκος, αμελητέα ωμική αντίσταση, απέχουν μεταξύ τους σταθερή απόσταση l και η βάση στήριξή τους είναι ηλεκτρικά μονωμένη. Η λεπτή ομογενής ράβδος ΚΛ μάζας m και μήκους l έχει τα άκρα της Κ και Λ σε ηλεκτρική επαφή με τους αγωγούς Αy και Γy' και βρίσκεται μέσα σε ομογενές μαγνητικό πεδίο έντασης Β με δυναμικές γραμμές κάθετες στο επίπεδο των αγωγών. Στο κέντρο της ράβδου έχει στερεωθεί το πάνω άκρο κατακόρυφου ιδανικού ελατηρίου σταθεράς k το άλλο άκρο του οποίου είναι ακλόνητο. Στην κατάσταση ισορροπίας το ελατήριο είναι συσπειρωμένο κατά Δl. 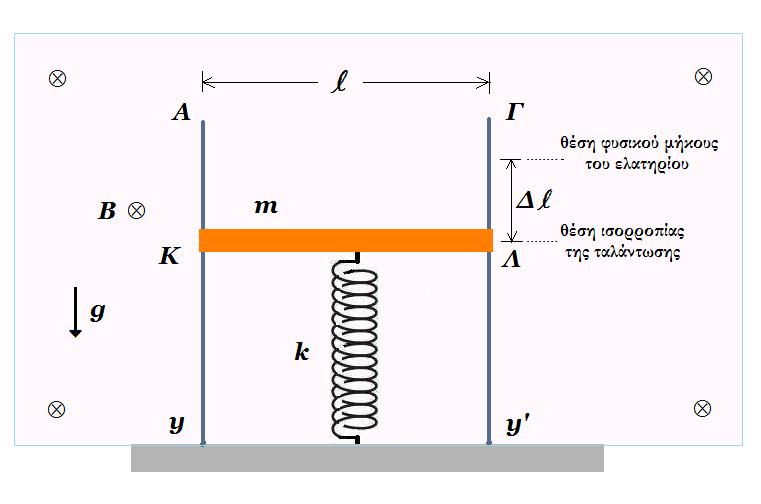
Εκτρέπουμε τη ράβδο από τη θέση ισορροπίας της μέχρι το ελατήριο να αποκτήση το φυσικό του μήκος και κάποια χρονική στιγμή την αφήνουμε ελεύθερη να εκτελέση απλή αρμονική ταλάντωση με σταθερά επαναφοράς k. Όταν η απομάκρυνση της ράβδου από τη θέση ισορροπίας της ισούται με Δl.3½/2 τότε η απόλυτη τιμή της Εεπαγ που αναπτύσεται στα άκρα της είναι ίση με :
(α) B g l /2 ( 3m/k )½ (β) B g l /4 ( m/k )½ (γ) B g l /2 ( m/k )½ όπου g το μέτρο της επιτάχυνσης της βαρύτητας.
ισορροπία ράβδου : m g = k Δl ω2 = k/m
x(t) = Δl ημ(ωt + 3π/2) υ(t) = ω Δl συν(ωt + 3π/2)
Εεπαγ = Β l υ = Β l ω Δl συν(ωt + 3π/2) = Εεπαγ(t)
x(t) = Δl ημ(ωt + 3π/2) => Δl.3½/2 = Δl ημ(ωt + 3π/2) => 3½/2 = ημ(ωt + 3π/2) =>
=> συν(ωt + 3π/2) = ± ½ => υ = ω Δl συν(ωt + 3π/2) = ± ω Δl ½
άρα Εεπαγ = Β l υ = Β l ( ± ω Δl / 2 ) = ± ½ Β l ( k/m )½ m g / k = ± ½ Β l g ( m/k )½
|Εεπαγ| = ½ Β l g Φm/k
ΣF = m a => m g - Fελατ = m a => m g - k x = m d2x/dt2 => d2x/dt2 + k/m x - g = 0 (1)
x(t) = Aημ(ωt + φ) υ(t) = dx/dt = ωA συν(ωt + φ) α(t) = dv/dt = d2x/dt2 = - ω2A ημ(ωt + φ)
(1) => - ω2 A ημ(ωt + φ) + k/m A ημ(ωt + φ) - g = 0
( k/m - ω2 ) A ημωt συνφ + ( k/m - ω2 ) A συνωt ημφ - g = 0
ΘΕΜΑ 9.
Ο οριζόντιος αγωγός Μ του σχήματος είναι απείρου μήκους και διαρρέεται από ρεύμα έντασης Ι1 = 40 Α. Ο αγωγός ΚΛ μήκους l = 1 m και ωμικής αντίστασης R = 7 Ω μπορεί να κινείται χωρίς τριβές με τα άκρα του πάνω στους αγωγούς ΑΓ και ΔΖ που είναι αμελητέας αντίστασης και βρίσκονται στο ίδιο οριζόντιο επίπεδο με τον αγωγό Μ. Η πηγή έχει ΗΕΔ Ε = 10 V και εσωτερική αντίσταση r = 3 Ω ενώ η ένταση του κατακόρυφου ομογενούς μαγνητικού πεδίου έχει μέτρο Β = 10-5 Τ. Όταν κλείσουμε τον διακόπτη δ να υπολογίσετε :
(α) τη σχέση που δίνει τη δύναμη Laplace την οποία δέχεται ο αγωγός ΚΛ λόγω του μαγνητικού πεδίου που δημιουργεί ο αγωγός Μ συναρτήσει της απόστασης d.
(β) την απόσταση d ώστε η ο αγωγός ΚΛ να ισορροπεί.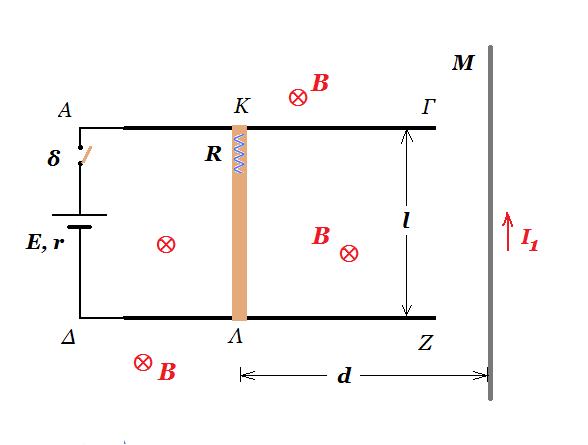
(α) i = E / (R + r) => i = 10 / (7 + 3) => i = 1 A
FL = 10-7 2 Ι1 i l / d = 10-7 2 40 1 1 / d = 8 10-6 / d
(β) B i l = 10-7 2 Ι1 i l / d => d = 10-7 2 Ι1 / B => d = 10-7 2 40 / 10-5 = 10-2 80 = 0,8 m
(α) m = 1 kg d = 0,8 m Ι1 = 40 ημ10t
i = ( E - B l v ) / (R + r) => i = ( 10 - 10-5 v ) / (7 + 3) => i = 1 - 10-6 v
FL = 10-7 2 Ι1 i l / (d-x) = 10-7 2 40 ημ10t 1 (1 - 10-6 v) / (d-x) = 8 10-6 (1 - 10-6 v) ημ10t / (d-x)
(β) ΣF = m a => B i l - 10-7 2 Ι1 i l / (d-x) = m a =>
=> a = 10-5 (1 - 10-6 v) - 8 10-6 (1 - 10-6 v) ημ10t / (0,8 - x)
ΘΕΜΑ 10.
Η ράβδος ΚΛ μάζας m = 2 kg και μήκους l = 1 m διαρρέεται από ρεύμα έντασης Ι = 10 Α και μπορεί να ολισθαίνει χωρίς τριβές μένοντας συνεχώς οριζόντια σε επαφή με τις δύο παράλληλες κατακόρυφους αγωγούς από μονωτικό υλικό. Το όλο σύστημα βρίσκεται μέσα σε ομογενές οριζόντιο μαγνητικό πεδίο έντασης Β = 1 Τ. Τη στιγμή t0 = 0 αφήνουμε την ράβδο ΚΛ ελεύθερη. Υπολογίστε :
(α) το ρυθμό μεταβολής της ταχύτητας της ράβδου
(β) το διάστημα που θα διανύσει μέχρι τη στιγμή t1 = 2 s
(γ) το ρυθμό μεταβολής της βαρυτικής δυναμικής ενέργειας και το ρυθμό μεταβολής της κινητικής ενέργειας της ράβδου μέχρι τη στιγμή t2 = 4 s. ( g = 10 m/s2 )
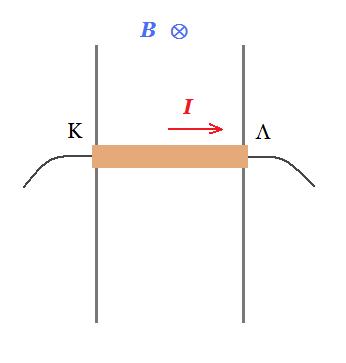
m g - B i l = m a => 2 10 - 1 10 1 = 2 a => a = 5 m/s2
y = ½ α t2 => y = ½ 5 22 => y = 10 m
t = 4 s v = a t = 5 4 = 20 m/s
U = m g (H - y) => dU/dt = m g ( - dy/dt ) => dU/dt = - m g vy Η : αρχικό ύψος y : διανυόμενο κατακόρυφο διάστημα
dU/dt = - m g v = - 2 10 20 = - 400 J/s μειώνεται η δυναμική βαρυτική ενέργεια της ράβδου ΚΛ καθώς πέφτει
K = ½ m v2 => dK/dt = ½ 2 m v dv/dt => dK/dt = m a v
dK/dt = m a v = 2 5 20 = 200 J/s αυξάνεται η κινητική ενέργεια της ράβδου ΚΛ καθώς πέφτει
i(t) = 10 ημ(10.t)
m g - B l i = m a => 2 10 - 1 1 10 ημ(10.t) = 2 a => a(t) = 10 - 5 ημ(10.t)
v(t) = 10.t + 0,5 συν(10.t) y(t) = 5.t2 + 0,05 ημ(10.t)
U = m g (H - y) => dU/dt = m g ( - dy/dt ) => dU/dt = - m g vy Η : αρχικό ύψος y : διανυόμενο κατακόρυφο διάστημα
dU/dt = - m g vy = - 2 10 [ 10.t + 0,5 συν(10.t) ] => dU/dt = - 200.t - 10 συν(10.t)
K = ½ m v2 => dK/dt = ½ 2 m v dv/dt => dK/dt = m a v
dK/dt = m a v = 2 [ 10 - 5 ημ(10.t) ] [ 10.t + 0,5 συν(10.t) ] =
= [ 10 - 5 ημ(10.t) ] [ 20.t + συν(10.t) ] =
= 200.t - 100.t ημ(10.t) + 10 συν(10.t) - 5 ημ(10.t) συν(10.t)
11. ΘΕΜΑ Γ 2020
Δύο παράλληλοι οριζόντιοι αγωγοί ΑΓ και ΔΖ μεγάλου μήκους και μηδενικής αντίστασης απέχουν μεταξύ τους απόσταση L = 1m. Τα άκρα Α και Δ συνδέονται με αγωγό αντίστασης R1 = 2Ω και τα άκρα Γ και Ζ με αγωγό αντίστασης R2 = 2Ω. Ο αγωγός ΑΓ έχει λίγο πριν το τέλος του ανοιχτό διακόπτη δ, όπως φαίνεται στο σχήμα. Ένας άλλος αγωγός ΚΛ, με μήκος (KΛ) = 1m έχει αντίσταση RΚΛ = 3Ω και μπορεί να ολισθαίνει χωρίς τριβές, μένοντας κάθετος και σε επαφή στα σημεία Κ και Λ με τους οριζόντιους αγωγούς ΑΓ και ΔΖ. Ο αγωγός ΚΛ αρχικά είναι ακίνητος. Κάποια χρονική στιγμή, την οποία θεωρούμε ως t=0, ασκούμε στο μέσο του αγωγού ΚΛ σταθερή δύναμη μέτρου F = 0,8N, η οποία είναι κάθετη στον αγωγό και η διεύθυνσή της ανήκει στο επίπεδο που ορίζουν οι αγωγοί ΑΓ και ΔΖ. Ο αγωγός ΚΛ αρχίζει να κινείται μέσα σε ομογενές μαγνητικό πεδίο έντασης B1 = 1T, που είναι κάθετο στο επίπεδο των αγωγών ΑΓ και ΔΖ, με φορά από τον αναγνώστη προς τη σελίδα.
Τη χρονική στιγμή t1 ο αγωγός ΚΛ, έχοντας αποκτήσει σταθερή οριακή ταχύτητα υορ , εξέρχεται από την περιοχή όπου η ένταση του μαγνητικού πεδίου είναι Β1 και εισέρχεται σε περιοχή, όπου η ένταση του μαγνητικού πεδίου είναι Β2 = 0, όπως φαίνεται στο σχήμα.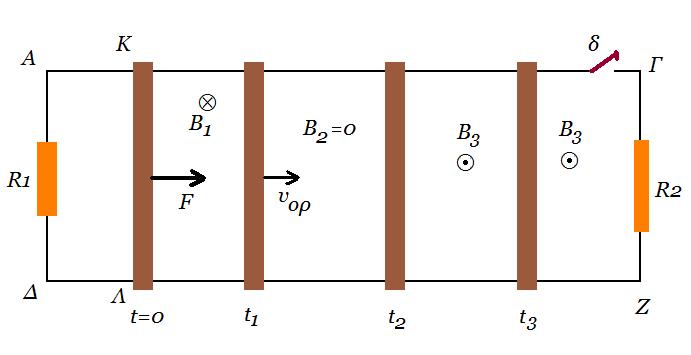
Γ1. Να περιγράψετε το είδος της κίνησης που εκτελεί ο αγωγός ΚΛ από τη χρονική στιγμή t=0 έως τη χρονική στιγμή t1 και να υπολογίσετε τη σταθερή οριακή ταχύτητα υορ.
Τη χρονική στιγμή t1 καταργούμε τη δύναμη F και τη χρονική στιγμή t2 ο αγωγός ΚΛ εισέρχεται σε περιοχή όπου υπάρχει ομογενές μαγνητικό πεδίο έντασης Β3, ίδιου μέτρου και αντίθετης κατεύθυνσης με την ένταση Β1.
Γ2. Να υπολογίσετε το μέτρο και να προσδιορίσετε τη φορά της εξωτερικής δύναμης F ', που πρέπει να ασκήσουμε στο μέσον του αγωγού ΚΛ, κάθετα
σε αυτόν και της οποίας η διεύθυνση ανήκει στο επίπεδο των αγωγών, ώστε ο αγωγός να συνεχίσει να κινείται με σταθερή ταχύτητα μέτρου υορ .
Γ3. Να υπολογίσετε τη θερμότητα Q, που εκλύεται στους αγωγούς του κυκλώματος από τη χρονική στιγμή t2 μέχρι μια άλλη χρονική στιγμή t3, αν
το επαγωγικό φορτίο που πέρασε από μία διατομή του αγωγού ΚΛ στο αντίστοιχο χρονικό διάστημα (t2 - t3) είναι qεπ = 0,2 C.
Τη χρονική στιγμή t3 κλείνουμε το διακόπτη δ και ο αγωγός ΚΛ, με την επίδραση της εξωτερικής δύναμης F ' , συνεχίζει την κίνησή του στην περιοχή όπου
υπάρχει το ομογενές μαγνητικό πεδίο έντασης Β3 και τελικά αποκτά νέα οριακή ταχύτητα.
Γ4. Να υπολογίσετε τη νέα οριακή ταχύτητα υορ, που αποκτά ο αγωγός, καθώς και την τάση VΚΛ στα άκρα του αγωγού ΚΛ και τις εντάσεις των ρευμάτων, που διαρρέουν τους αντιστάτες R1 και R2 , όταν αυτός κινείται με τη νέα του οριακή ταχύτητα.
Γ1. H ράβδος ΚΛ κινείται μέσα σε μαγνητικό πεδίο, τα ηλεκτρόνια της ράβδου δέχονται δύναμη Lorenz και κινούνται προς το άκρο Λ το οποίο φορτίζεται αρνητικά ενώ το άκρο Κ φορτίζεται θετικά. Αναπτύσσεται τάση από επαγωγή στα άκρα της ράβδου, Εεπαγ = Β1 . υ . l (1) Έχουμε κλειστό κύκλωμα : Εεπαγ = i . ( R1 + RΚΛ ) (2) Η ράβδος διαρρέεται από ρεύμα μέσα σε μαγνητικό πεδίο, οπότε δέχεται δύναμη Laplace : FL = i .B1 . l (3)
(1) , (2) , (3) => FL = i .B1 . l = Εεπαγ / ( R1 + RΚΛ ) . Β1 . l = Β1 . υ . l / ( R1 + RΚΛ ) . Β1 . l =>
=> FL = Β12 . l2 . υ / ( R1 + RΚΛ ) (4)
Η ράβδος κινείται : ΣF = m.a => F - FL = m.a
H επιτάχυνση της ράβδου μειώνεται συνέχεια και κάποια στιγμή μηδενίζεται, τότε :
F - FL = 0 => F = FL = Β12.l2.υ / (R1 + RΚΛ) => F .(R1 + RΚΛ) / (Β1.l)2 = υ = υορ οριακή ταχύτητα ράβδου
υορ = F .( R1 + RΚΛ ) / (Β1 .l)2 = 0,8 .( 2 + 3 ) / (1 .1)2 = 4 m/s = υορ στην περιοχή όπου Β2 = 0 η ράβδος κινείται με σταθερή ταχύτητα 4 m/s
Γ2. H ράβδος όταν εισέρχεται στην περιοχή Β3 (αντίθετο του Β1) δέχεται μόνο τη δύναμη Laplace οριζόντια προς τα αριστερά λόγω κλειστού κυκλώματος αφού η F καταργείται. Για να διατηρείται η ταχύτητα σταθερή πρέπει να ασκηθεί F ' αντίθετη της δύναμης Laplace :
F' = FL = Β12 . l2 . υορ / ( R1 + RΚΛ ) = 1 . 1 . 4 / (2 + 3) = 0,8 Ν προς τα δεξιά
Γ3. Από τη ράβδο περνά φορτίο qεπ = 0,2 C. qεπ = i . Δt
1oς τρόπος
Εεπαγ = B3 . l . υορ = i .( R1 + RΚΛ ) => B3 . l . υορ /( R1 + RΚΛ ) = i => 1. 1. 4 / 5 = i => i = 0,8 A
επαγωγικό φορτίο qεπ = i . Δt => 0,2 = 0,8 . Δt => Δt = 0,2/0,8 = 0,25 sec
η ράβδος σε χρόνο 0,25 sec διανύει απόσταση Δx = υορ . Δt = 4 m/s .0,25 s = 1 m
θερμότητα Qθερμ = i2 .( R1 + RΚΛ ). Δt = 0,82 . 5 . 0,25 = 0,8 Joule
2oς τρόπος
Εεπαγ = ΔΦ/Δt => B3 .l .υορ = ΔΦ/Δt => i .( R1 + RΚΛ ) = B3 .ΔA/Δt =>
=> i .Δt .( R1 + RΚΛ ) = B3 .Δx.l =>
=> qεπ .( R1 + RΚΛ ) = B3 .Δx.l => qεπ .( R1 + RΚΛ ) / B3.l = Δx =>
=> 0,2 .( 2 + 3 ) / 1.1 = Δx = 1 m η ράβδος διανύει απόσταση 1 m.
θερμότητα Qθερμ = FL . Δx = 0,8 N . 1 m = 0,8 J
Γ4. Έχουμε κλειστό κύκλωμα R1 , R2 παράλληλη σύνδεση R1,2 = R1 . R2 / (R1+R2) = 1 Ω
Η ράβδος κινείται μέσα στο μαγνητικό πεδίο Β3 δέχεται δύναμη Laplace ΣF = m.a => F - FL = m.a H επιτάχυνση της ράβδου μειώνεται συνέχεια και κάποια στιγμή μηδενίζεται, τότε : F - FL = 0 => F' = FL = Β32 . l2 . υ / ( R1 + RΚΛ ) => F' .( R1,2 + RΚΛ ) / (Β3 .l)2 = υ = υ'ορ οριακή ταχύτητα ράβδου
υ'ορ = F' .( R1,2 + RΚΛ ) / (Β3 .l)2 = 0,8 .( 1 + 3 ) / (1 .1)2 = 3,2 m/s = υ'ορ
τότε Ε'επαγ = Β3 . l .υ'ορ = 1 . 1. 3,2 = 3,2 Volt
i' = Ε'επαγ / ( R1,2 + RΚΛ ) = 3,2 / 4 = 0,8 A επαγωγικό ρεύμα
VΛΚ = Ε'επαγ - i' . RΚΛ = 3,2 - 0,8 A . 3 Ω = 3,2 - 2,4 = 0,8 Volt
i'1 = VΛΚ / R1 = 0,8 / 2 = 0,4 A & i'2 = VΛΚ / R2 = 0,8 / 2 = 0,4 A
Θ Ε Μ Α 12
Τα άκρα πηνίου Π1 συνδέονται με στρεφόμενο πλαίσιο Ν περιελίξεων εμβαδού επιφάνειας Α (κάθε μίας), το οποίο περιστρέφεται με σταθερή συχνότητα f, μέσα σε σταθερό μαγνητικό πεδίο εντάσεως Β. Το πηνίο Π1 έχει Ν1 σπείρες, μήκος L1 και αντίσταση R1. Λόγω της περιστροφής του πλαισίου επάγεται τάση στα άκρα του πηνίου Π1.
α) Εκφράστε την επαγώμενη τάση στα άκρα του πηνίου Π1 συναρτήσει του χρόνου.
β) Εκφράστε το ηλεκτρικό ρεύμα που διαρρέει το πηνίο Π1 ως προς τον χρόνο.
γ) Εκφράστε την ένταση του μαγνητικού πεδίου που εμφανίζεται στο εσωτερικό του πηνίου Π1.
δ) Γύρω απο το μέσον του πηνίου Π1 τυλίγουμε πηνίο Π2 της ιδίας ακτίνας r (για κάθε σπείρα), που έχει Ν2 σπείρες, μήκος L2 ( N2 < N1 , L2 < L1 ) και αντίσταση R2. Εκφράστε την επαγώμενη τάση στα άκρα του πηνίου Π2 συναρτήσει του χρόνου.
ε) Τα άκρα του πηνίου Π2 συνδέονται με λαμπτήρα αντίστασης RΛ, εκφράστε το ηλεκτρικό ρεύμα που διαρρέει τον λαμπτήρα ως προς τον χρόνο.
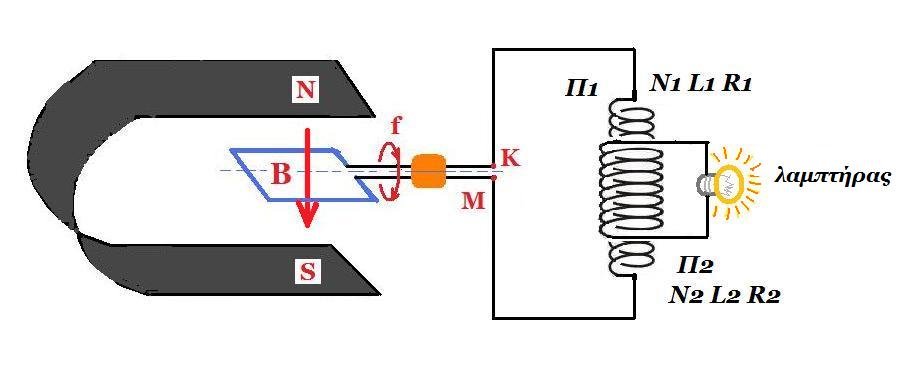
α) Εεπαγ(1) = -Ν.ΔΦ/Δt, Εεπαγ(1) = - Ν.Φ'(t) = - Ν.[B.A.συν(ω.t)]' = -Ν.B.A.ω.(-ημωt) = Ν.B.A.2πf.ημ(2πf.t) εναλλασσόμενη τάση : V1 = Vo1 . ημ(2πf.t) με πλάτος : Vo1 = Ν.B.A.2πf
β) Ι1 = Εεπαγ(1) / R1 = Ν.B.A.2πf.ημ(2πf.t) / R1 => Ι1(t) = Ν.B.A.2πf / R1 .ημ(2πf.t)
γ) Επειδη το πηνίο Π1 διαρρέεται από ρεύμα εμφανίζεται μαγνητικό πεδίο που στο κέντρο του έχει ένταση : Β1 = μο . Ν1 . Ι1 / L1 => Β1(t) = (μο.Ν1.Ν.Β.Α.2πf) / (R1.L1) . ημ(2πf.t)
δ) Tο εμβαδόν κάθε σπείρας του πηνίου Π1 είναι ίσο με το αντίστοιχο του Π2, δηλαδή S=π.r2. Μέσα από κάθε σπείρα του πηνίου Π2 διέρχεται μαγνητική ροή Φ2 = Β1 . S αλλά το Π2 έχει Ν2 σπείρες. Συνεπώς από τις σπείρες του πηνίου Π2 διέρχεται μαγνητική ροή : Φ2 = Β1 . S . N2 = Bo1.ημ(2πf.t) .S.N2 = Φ2(t). Eπειδή η μαγνητική ροή μεταβάλλεται με τον χρόνο, επάγεται τάση στα άκρα του Π2 :
Εεπαγ(2) = -Φ2'(t) = - Bo1.S.N2.2πf.συν(2πf.t) => Eεπαγ(2) (t) = - (μο.Ν1.Ν.Β.Α.4π2f2.S.N2) / (R1.L1) . συν(2πf.t)
ε) Το πηνίο Π2 συνδέεται με τον λαμπτήρα σε σειρά οπότε κυκλοφορεί ρεύμα που έχει ένταση :
Ι2 = Εεπαγ(2) / (R2 + RΛ) => I2(t) = - ( μο.Ν1.Ν.Β.Α.4π2f2.S.N2 ) / L1.R1.(R2+RΛ) . συν(2πf.t)
( 4π.10-7 . 1000 . 10 . 0,1.2½ . 0,1 . 4π2f2 . π.10-2 . 200 ) / 0,2 . 10 . ( 20 + 5 ) =
( 4π.10-7 . 1000 . 2½ . 0,1 . 4π2f2 . π.10-2 . 100 ) / ( 20 + 5 ) = ( 4.10-4 . 2½ . 4π2f2 ) / ( 20 + 5 ) = 4. 2½ =>
4π2f2 = 25 . 104 => f = 250 / π Hz
Θ Ε Μ Α 13
Τα άκρα πηνίου Π1 συνδέονται με στρεφόμενο πλαίσιο Ν = 10 περιελίξεων εμβαδού επιφάνειας Α = 0,1 m2 (κάθε μίας), το οποίο περιστρέφεται με σταθερή συχνότητα f, μέσα σε ομογενές μαγνητικό πεδίο εντάσεως Β = 0,1.2½ T. Το πηνίο Π1 έχει Ν1 = 1000 σπείρες, μήκος L1 = 0,2 m και αντίσταση R1 = 10 Ω. Γύρω απο το μέσον του πηνίου Π1 τυλίγουμε πηνίο Π2 της ιδίας ακτίνας r = 0,1 m (για κάθε σπείρα), που έχει Ν2 = 200 σπείρες, μήκος L2 = 0,1 m και αντίσταση R2 = 20 Ω. Τα άκρα του πηνίου Π2 συνδέονται με λαμπτήρα με χαρακτηριστικά: <20V, 80W>. Με ποια συχνότητα f πρέπει να περιστρέφεται το πλαίσιο για να φωτοβολεί κανονικά ο λαμτήρας;
P = V . i => i = P/V = 80 W / 20 V = 4 A = Ιεν Ι0 = 4.2½ Α Rλ = V / i = 20 V / 4 A => Rλ = 5 Ω.
Εεπαγ(1) = -Ν.|ΔΦ|/Δt, Εεπαγ(1) = - Ν.Φ'(t) = - Ν.[B.A.συν(ω.t)]' = -Ν.B.A.ω.(-ημωt) = Ν.B.A.2πf.ημ(2πf.t) == 10 . 0,1.2½ . 0,1 . 2πf . ημ(2πf.t) => Εεπαγ(1) = 0,1.2½ . 2πf . ημ(2πf.t)
Ι1 = Εεπαγ / R1 = 0,01.2½ . 2πf . ημ(2πf.t)
Β1 = μο . Ν1 . Ι1 / L1 => Β1 = 4π.10-7 . ( 1000 / 0,2 ) . 0,01.2½ . 2πf . ημ(2πf.t) = 2π.10-5 . 2½ . 2πf . ημ(2πf.t)
S=π.r2 = π.10-2 m2
Φ2 = Β1 . S . N2 => Φ2 = 2π.10-5 . 2½ . 2πf . ημ(2πf.t) . π.10-2 . 200 = 4.2½ . 10-4 . 2πf . ημ(2πf.t)
Εεπαγ(2) = - Φ2'(t) => Εεπαγ(2) = - 4.2½ . 10-4 . (2πf)2 . συν(2πf.t)
Ι2 = Εεπαγ(2) / (R2 + RΛ) => Ι2 = - 4.2½ . 10-4 . (2πf)2 . συν(2πf.t) / (20 + 5)
Ι0 = 4.2½ .10-4 .(2πf)2 / 25 = 4.2½ Α => (2πf)2 = 25 . 104 => 2πf = 500 => f = 250/π Hz
ΘΕΜΑ 14.

Κυκλικός αγωγός & σωληνοειδές (§ 4.2 Σχολικού βιβλίου Α’ τεύχος)
Δίνεται το κύκλωμα του σχήματος, το οποίο αποτελείται από ηλεκτρική πηγή με ΗΕΔ Ε = 24 V και εσωτερική αντίσταση r = 2 Ω, κυκλικό αγωγό ακτίνας ρ = 2π cm και ωμικής αντίστασης Rκ = 6 Ω, σωληνοειδές με Ν=1.000 σπείρες, μήκος L = 20 cm , αντίσταση μιας σπείρας R* = 0,003 Ω / σπείρα και ολικής ωμικής αντίστασης RΣ , αντίσταση R = 2 Ω, τρεις διακόπτες, μεταλλικούς αγωγούς (σύρματα) αμελητέας ωμικής αντίστασης.
Αρχικά και οι τρεις διακόπτες είναι ανοικτοί.
α. Κλείνουμε το διακόπτη (δ1). Να υπολογίσετε την ένταση του μαγνητικού πεδίου (μέτρο και κατεύθυνση) στο κέντρο του κυκλικού ρευματοφόρου αγωγού.
β. Κλείνουμε και το διακόπτη (δ2). Να υπολογίσετε
β1. το μέτρο της έντασης του μαγνητικού πεδίου στο κέντρο του κυκλικού ρευματοφόρου αγωγού.
β2. το μέτρο της έντασης του μαγνητικού πεδίου στο κέντρο του σωληνοειδούς
β3. Να συγκρίνετε τα μέτρα των δύο εντάσεων.
γ. Κλείνουμε και το διακόπτη (δ3). Να υπολογίσετε
γ1. το μέτρο της έντασης του μαγνητικού πεδίου στο κέντρο του κυκλικού
ρευματοφόρου αγωγού.
γ2. το μέτρο της έντασης του μαγνητικού πεδίου στο άκρο του σωληνοειδούς.
Δίνεται η σταθερά kμ = 10-7 Ν / Α2 .
i = E / ( Rκ + r ) = 24 / ( 6 + 2 ) = 3 A Bκ = 10-7 2π i / ρ = 10-7 2π 3 / 2π.10-2 = 3 10-5 Τ
RΣ = R* N = 0,003 1000 = 3Ω Rκ,Σ = 6 3 / (6 + 3) = 2Ω
i = E / ( Rκ,Σ + r ) = 24 / ( 2 + 2 ) = 6 A Vπολική = Ε - i r = 24 - 6 2 = 12 V
iκ = Vπολική / Rκ = 12 / 6 = 2 A Bκ = 10-7 2π iκ / ρ = 10-7 2π 2 / 2π.10-2 = 2 10-5 Τ
iΣ = Vπολική / RΣ = 12 / 3 = 4 A Bκ = 4π 10-7 iΣ N / L = 4π 10-7 4 103 / 0,2 = 8π 10-3 Τ
1/Rολική = 1/RΣ + 1/Rκ + 1/R = 1/3 + 1/6 + 1/2 = ( 2 + 1 + 3 ) / 6 = 1 => Rολική = 1 Ω
i = E / ( Rκ,Σ + r ) = 24 / ( 1 + 2 ) = 8 A Vπολική = Ε - i r = 24 - 8 2 = 8 V
iκ = Vπολική / Rκ = 8 / 6 = 4/3 A Bκ = 10-7 2π iκ / ρ = 10-7 2π 4/3 / 2π.10-2 = 4/3 10-5 Τ
iΣ = Vπολική / RΣ = 8 / 3 = 8/3 A Bκ = 4π 10-7 iΣ N / L = 4π 10-7 8/3 103 / 0,2 = 16π/3 10-3 Τ
ΘΕΜΑ 15.

Ελατήρια και δύναμη Laplace (§ 4.3 Σχολικού βιβλίου Α’ τεύχος)
Δύο κατακόρυφα ιδανικά ελατήρια (Ε1) και (Ε2) είναι πάνω στην ίδια κατακόρυφο και έχουν ίδια σταθερά ελατηρίου Κ=100 N/m. Το (Ε1) είναι στερεωμένο στο ανώτερο σημείο του και το (Ε2) στο κατώτερο. Τα άλλα άκρα των ελατηρίων, που έχουν το φυσικό τους μήκος, βρίσκονται στο ίδιο σημείο. Τα ελατήρια βρίσκονται μέσα σε ομογενές οριζόντιο μαγνητικό πεδίο έντασης μέτρου Β = 1 Τ και φοράς που φαίνεται στο σχήμα. Ευθύγραμμος αγωγός (Ε) μήκους L = 1 m και ωμικής αντίστασης RE = 2 Ω που διατηρείται συνεχώς οριζόντιος, συνδέεται με τα ελεύθερα άκρα των δύο ελατηρίων με τέτοιο τρόπο, ώστε να μην αλλοιώνεται το ηλεκτρικό ρεύμα, όταν διαρρέει τον (Ε). Ο αγωγός (Ε) συνδέεται μέσω ηλεκτρικού διακόπτη (δ) και με αβαρή σύρματα αμελητέας ωμικής αντίστασης με ηλεκτρική πηγή ΗΕΔ Ε = 8 V και εσωτερικής αντίστασης r = 2 Ω. Δίνεται το μέτρο της επιτάχυνσης της βαρύτητας g = 10 m/s2 . Αρχικά ο διακόπτης (δ) είναι ανοικτός, οπότε το (Ε1) είναι επιμηκυμένο κατά y = 1 cm, όταν ο αγωγός ισορροπεί.
Α. Η μάζα του αγωγού (Ε) είναι
α. m = 200 g β. m = 500 g γ. m = 1 kg
Να επιλέξετε τη σωστή απάντηση. Να αιτιολογήσετε την επιλογή σας.
Β. Κλείνουμε το διακόπτη (δ). Όταν ο αγωγός ισορροπεί, η επιμήκυνση του ελατηρίου (Ε1) είναι
α. 0 β. 0,5 cm γ. 1 cm
Να επιλέξετε τη σωστή απάντηση. Να αιτιολογήσετε την επιλογή σας.
ΣF = 0 => m g = k1 y + k2 y => m 10 = 100 0,01 + 100 0,01 => m = 2 / 10 = 0,2 kg = 200 g
i = E / ( R + r ) = 8 V / ( 2 Ω + 2 Ω ) => i = 2 A FL = B i l = 1 2 1 = 2 N
ΣF = 0 => k1 y + k2 y + FL - m g = 0 => 100 y + 100 y + 2 - 0,2 10 = 0 => y = 0
ΘΕΜΑ 16.

Πλαίσιο κινούμενο σε Ο.Μ.Π. (§ 4.6 Σχολικού βιβλίου Α’ τεύχος)
Ορθογώνιο αγώγιμο πλαίσιο ΑΓΔΖ έχει μήκος α = (ΑΓ) = (ΔΖ) = 60 cm και πλάτος β = (ΑΖ) = (ΓΔ) = 20 cm. Το πλαίσιο κινείται με σταθερή ταχύτητα υ = 0,1 m/s στο επίπεδό του, με ταχύτητα παράλληλη προς το μήκος του. Η ωμική αντίσταση του πλαισίου είναι R = 0,1 Ω. Τη χρονική στιγμή t0 = 0 το πλαίσιο αρχίζει να εισέρχεται σε ομογενές μαγνητικό πεδίο πλάτους γ = 40 cm, έντασης μέτρου Β =1 Τ και διεύθυνσης κάθετης στο επίπεδο του πλαισίου, όπως φαίνεται στο σχήμα. Από τη χρονική στιγμή t0 = 0 έως τη χρονική στιγμή που ολόκληρο το πλαίσιο εξέρχεται από το μαγνητικό πεδίο, να κάνετε τις γραφικές παραστάσεις
α. μαγνητικής ροής (Φ) με το χρόνο (t)
β. τάσης από επαγωγή (Εεπ) με το χρόνο (t)
γ. έντασης ηλεκτρικού ρεύματος (Ι) με το χρόνο (t)
δ. δύναμης Laplace (FL) με το χρόνο (t)
x = v t => 0,4 m = 0,1 m/s t => t1 = 4 s 0,6 m = 0,1 m/s t => t2 = 6 s
η πλευρά ΓΔ του πλαισίου σε χρόνο t1 = 4 s μετακινείται από το ένα άκρο της περιοχής του μαγνητικού πεδίου μέχρι την άλλη άκρη, τα ηλεκτρόνια της μετακινούνται προς το άκρο Δ που φορτίζεται αρνητικά ενώ το άκρο Γ θετικά, αναπτύσσεται Εεπαγ = Β υ (ΓΔ) = 1 0,1 0,2 = 0,02 Volt Φ(t) = 0,02 t 0 < t < 4 s i = Εεπαγ/R = 0,02 / 0,1 = 0,2 A FL = B i (ΓΔ) = 1 0,2 0,2 = 0,04 N μετά τη στιγμή t1 = 4 s η πλευρά ΓΔ εξέρχεται μέχρι την στιγμή t2 = 6 s που η πλευρά ΑΖ εισέρχεται στο μαγνητικό πεδίο οπότε για χρονικό διάστημα t2 - t1 = 6 s - 4 s =2s έχουμε Εεπαγ = 0 Φ = 0 i = 0 FL = 0 μετά καθώς η πλευρά ΑΖ εισέρχεται στο μαγνητικό πεδίο τα ηλεκτρόνια της μετακινούνται προς το άκρο Ζ που φορτίζεται αρνητικά ενώ το άκρο Α θετικά, αναπτύσσεται Εεπαγ = Β υ (ΑΖ) = 1 0,1 0,2 = 0,02 Volt Φ(t) = 0,02 t 6 < t < 10 s μέχρι η ΑΖ φθάσει στην άκρη του πεδίου i = Εεπαγ/R = 0,02 / 0,1 = 0,2 A με φορά αντίθετη ως προς το προηγούμενο ρεύμα και FL = B i (ΑΖ) = 1 0,2 0,2 = 0,04 N
ΘΕΜΑ 17.

Ηλεκτρεγερτική Δύναμη από επαγωγή (§ 4.6 Σχολικού βιβλίου Α’ τεύχος)
Πάνω σε οριζόντιο επίπεδο βρίσκονται δύο παράλληλοι αγωγοί αμελητέας ωμικής αντίστασης και μεγάλου μήκους, οι οποίοι απέχουν απόσταση L. Οι αγωγοί στο αριστερό τους άκρο συνδέονται με αγωγό μήκους L και αμελητέας ωμικής αντίστασης. Τέταρτος αγωγός (Α) έχει ωμική αντίσταση R, μήκος L και είναι
πάντοτε σε επαφή με τους δύο παράλληλους αγωγούς, ενώ μπορεί να κινείται παράλληλα στον εαυτό του. Το σύστημα είναι μέσα σε ομογενές κατακόρυφο μαγνητικό πεδίο έντασης 𝛣⃗ . Αρχικά ο αγωγός είναι ακίνητος. Κάποια χρονική στιγμή αρχίζει να ασκείται στον αγωγό (Α) προς τα δεξιά σταθερή οριζόντια δύναμη μέτρου F και διεύθυνσης ίδιας με τους παράλληλους αγωγούς.
Α. Να περιγράψετε την κίνηση που θα κάνει ο αγωγός (Α).
Β. Το μέτρο της σταθερής ταχύτητας υορ που θα αποκτήσει ο αγωγός (Α) είναι:
α. υορ = 𝐹·𝑅 / 𝐵2·𝐿2 β. υορ = 2·𝐹·𝑅 / 𝐵2·𝐿2 γ. υορ = 4·𝐹·𝑅 / 𝐵2·𝐿2
Να επιλέξετε τη σωστή απάντηση. Να αιτιολογήσετε την επιλογή σας.
Να θεωρήσετε ότι κατά την κίνηση του αγωγού (Α) η τριβή είναι αμελητέα
κινούμενη η ράβδος μέσα στο μαγνητικό πεδίο τα ηλεκτρόνια της δέχονται δύναμη Lorenz και μετακινούνται στο ένα άκρο της ράβδου το οποίο φορτίζεται αρνητικά ενώ το άλλο άκρο φορτίζεται θετικά οπότε αναπτύσσεται επαγωγική τάση Εεπαγ = B l v στα άκρα της ράβδου με συνέπεια να διαρρέεται από ρεύμα το κλειστό κύκλωμα i = Εεπαγ / R = B l v / R οπότε η ράβδος δέχεται δύναμη Laplace FL = B i l = B2 l2 v / R έχουμε ΣF = m a => F - FL = m a => F - B2 l2 v / R = m a όσο κινείται η ράβδος περισσότερα ηλεκτρόνια, δεχόμενα δυνάμη Lorenz, μετακινούνται στο άκρο της ράβδου με συνέπεια να αυξάνεται η Εεπαγ οπότε μειώνεται η επιτάχυνση α μέχρι να μηδενισθεί τότε F - B2 l2 v / R = 0 => F = B2 l2 v / R => v = F R / B2 l2 = υορ η ράβδος αποκτά οριακή ταχύτητα δηλαδή σταθερή ταχύτητα με την οποία θα κινείται από τη στιγμή αυτή και μετά
ΘΕΜΑ 18.
Ηλεκτρεγερτική Δύναμη από επαγωγή (Κεφ. 5 Σχολικού βιβλίου Β’ τεύχος)
Εναλλασσόμενο ρεύμα έντασης i = 4·ημ(50πt) (SI) διαρρέει αντιστάτη αντίστασης R=20 Ω.
α. Να υπολογίσετε το πλάτος Ι0 της έντασης, την ενεργό τιμή Ιεν της έντασης, τη συχνότητα f και την περίοδο Τ του εναλλασσόμενου ρεύματος.
β. Να υπολογίσετε το μέσο ρυθμό με τον οποίο εκλύεται θερμότητα από την αντίσταση στο περιβάλλον.
γ. Να υπολογίσετε τη θερμότητα Q που εκλύεται από την αντίσταση σε χρονικό διάστημα Δt = 1 min.
δ. Να υπολογίσετε το ρυθμό με τον οποίο εκλύεται θερμότητα από την αντίσταση στο περιβάλλον τη χρονική στιγμή t = 1/300 s.
ε. Πόσο θα έπρεπε να ήταν το πλάτος Ι0 της έντασης του ρεύματος, ώστε ο μέσος ρυθμός με τον οποίο εκλύεται θερμότητα από την αντίσταση στο περιβάλλον να ήταν τετραπλάσιος
i(t) = 4·ημ(50πt)
α. I0 = 4 A Iεν = 4 / 2½ Α = 4 . 0,7 Α = 2,8 Α
ω = 50 π rad/s f = ω/2π = 25/π Hz T = 1/f = π/25 s
β. dQθερμ /dt = PΜ = Iεν 2 R = 16/2 . 20 = 160 Watt = 160 Joule/sec
γ. Q = P t = 160 W . 60 s = 9600 J
δ. P(t) = V(t) i(t) = i(t)2 R = 16·ημ2(50πt) 20 = 320 ·ημ2(50πt)
P(1/300) = 320 ·ημ2(50π 1/300) = 320 ·ημ2(π/6) = 320 (½)2 = 320 .1/4 = 80 Watt
ε. PΜ = 4 160 Watt => Iεν2 R = 640 => Iεν2 = 640 / 20 = 32 => Ιεν = 32½ Α = 4.2½ Α διπλασιάζεται το ρεύμα
ΘΕΜΑ 19.
Τετραγωνικό συρμάτινο πλαίσιο αμελητέας αντίστασης αποτελείται από Ν=100 σπείρες εμβαδού Α=100 cm2 η κάθε μία. Το πλαίσιο βρίσκεται μέσα σε ομογενές μαγνητικό πεδίο έντασης Β = 1 Τ και περιστρέφεται με σταθερή γωνιακή ταχύτητα μέτρου ω γύρω από άξονά του, που είναι κάθετος στις δυναμικές γραμμές του μαγνητικού πεδίου και διέρχεται από τα μέσα των δύο απέναντι πλευρών του. Το πλαίσιο συμπληρώνει μία περιστροφή γύρω από τον άξονα περιστροφής του κάθε 0,1π s. Από την περιστροφική κίνηση του πλαισίου παράγεται εναλλασσόμενη τάση της μορφής V = V0·ημ(ωt), η οποία εφαρμόζεται μέσω δακτυλίων στα άκρα θερμικής συσκευής που λειτουργεί με εναλλασσόμενο ρεύμα και έχει ενδείξεις κανονικής λειτουργίας 40 W/20 V.
Γ1. Να γράψετε την εξίσωση της εναλλασσόμενης τάσης και της έντασης του εναλλασσόμενου ρεύματος που διαρρέει τη θερμική συσκευή.
Γ2. Να διερευνήσετε αν η θερμική συσκευή λειτουργεί κανονικά και να υπολογίσετε το ποσό της θερμότητας που εκλύεται από τη θερμική συσκευή σε χρονικό διάστημα 100 περιόδων του εναλλασσόμενου ρεύματος.
Γ3. Να γράψετε τη χρονική εξίσωση της ισχύος που καταναλώνει η συσκευή και να σχεδιάσετε τη γραφική της παράσταση σε βαθμολογημένους άξονες για το χρονικό διάστημα 0 < t < 0,2 π s.
Γ4. Να υπολογίσετε το ποσοστό μεταβολής της γωνιακής συχνότητας περιστροφής του πλαισίου, ώστε η συσκευή να λειτουργεί κανονικά.
T = 0,1π s ω = 2π/Τ = 2π / 0,1π = 20 rad/s A = 100 cm2 = 10-2 m2
i = P/V = 40 W / 20 V = 2 A = Iεν Ι0 = 2 2½ Α R = V/i = 20 V / 2 A = 10 Ω
V0 = ω B A N => V0 = 20 1 10-2 100 => V0 = 20 V Vεν = 20/2½ V = 10 2½ V < 20 V η συσκευή υπολειτουργεί
V = V0·ημ(ωt) = 20·ημ(20t) i = V/R = 2·ημ(20t) PM = V0 I0 / 2 = 20 Watt μέση ισχύς
Q = P t = 20 W 100 0,1π s = 200.π Joule θερμότητα
P(t) = V(t) i(t) = 40 ημ2(20t)
V0 = ω B A N => 20 2½ = ω 1 10-2 100 => ω = 20 2½ rad/s = 20 1,4 rad/s = 28 rad/s
Δω / ω = 28-20 / 20 = 8 / 20 = 0,4 ή 40%
ΘΕΜΑ 20.
Δύο κατακόρυφες μεταλλικές ράβδοι μεγάλου μήκους AΓ και ΓΖ απέχουν μεταξύ τους
απόσταση l = 1,5 m, έχουν αμελητέα ωμική αντίσταση στηρίζονται σε μονωτική βάση.
Οριζόντιος ευθύγραμμος αγωγός ΚΛ μήκους l = 1,5 m, μάζας m, ωμικής αντίστασης R=4Ω συγκρατείται ακίνητος έχοντας τα άκρα του σε επαφή με τις παράλληλες ράβδους.
Το σύστημα ράβδοι – αγωγός βρίσκεται σε ομογενές μαγνητικό πεδίο με ένταση Β = 2 Τ και δυναμικές γραμμές κάθετες στο επίπεδο της διάταξης. Με σύρματα αμελητέας αντίστασης συνδέουμε τις κατακόρυφες ράβδους με κυκλικό μεταλλικό αγωγό και σωληνοειδές όπως απεικονίζεται στο ακόλουθο σχήμα.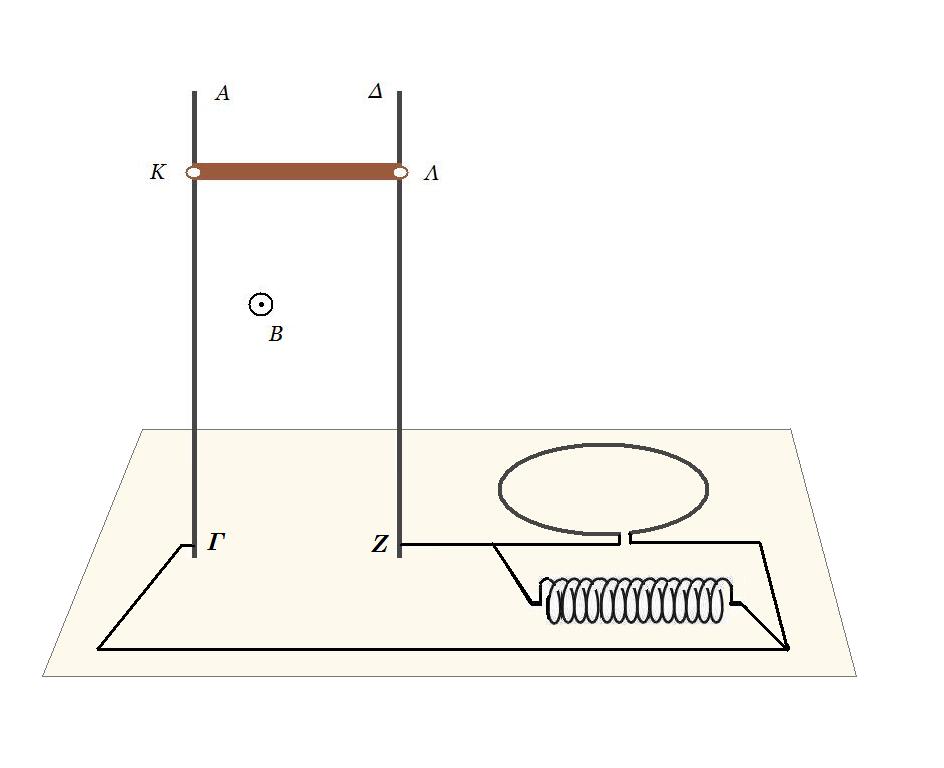 Ο κυκλικός αγωγός έχει ακτίνα 0,5 m και αντίσταση Rκ = 18 Ω ενώ το σωληνοειδές έχει 100 σπείρες ανά μέτρο και αντίσταση Rσ.
Ο κυκλικός αγωγός έχει ακτίνα 0,5 m και αντίσταση Rκ = 18 Ω ενώ το σωληνοειδές έχει 100 σπείρες ανά μέτρο και αντίσταση Rσ.
Τη χρονική στιγμή t0 = 0 αφήνουμε ελεύθερο τον αγωγό ΚΛ, ο οποίος αρχίζει την καθοδική του κίνηση χωρίς τριβές κάθετα στις ράβδους, με τα άκρα του πάνω σ’ αυτές και τη χρονική στιγμή t1 αποκτά σταθερή ταχύτητα υ = 10 m/s.
Δ1. Να αποδείξετε ότι κατά την κίνηση του αγωγού ΚΛ, αν η ισχύς που γίνεται θερμότητα στο σωληνοειδές είναι διπλάσια προς την αντίστοιχη ισχύ στον κυκλικό αγωγό (Pσ = 2Pκ), η αντίσταση όλης της διάταξης είναι Rολ=10 Ω.
Δ2. Να υπολογίσετε τη μάζα του αγωγού.
Δ3. Να υπολογίσετε τη διαφορά δυναμικού που εμφανίζεται στα άκρα του αγωγού ΚΛ μετά τη χρονική στιγμή t1.
Δ4. Να σχεδιάσετε τις εντάσεις των μαγνητικών πεδίων στο κέντρο του κυκλικού αγωγού και του σωληνοειδούς και να υπολογίσετε τα μέτρα τους.
Δ5. Μετά τη χρονική στιγμή t1, να υπολογίσετε τη μεταβολή της δυναμικής του ενέργειας του αγωγού ΚΛ στο χρονικό διάστημα στο οποίο στον κυκλικό αγωγό έχει παραχθεί θερμότητα Q = 7,2 J. Πόση θερμότητα αναπτύσσεται στο κύκλωμα στο ίδιο χρονικό διάστημα;
Δ6. Μελετήστε την κίνηση της ράβδου ΚΛ
η ράβδος ΚΛ κινείται προς τα κάτω κόβει δυναμικές γραμμές του μαγνητικού πεδίου τα ηλεκτρόνια της ράβδου κινούνται προς το άκρο Λ που φορτίζεται αρνητικά αναπτύσσεται τάση εξ' επαγωγής : Εεπαγ = Β υ l οπότε το κύκλωμα διαρρέεται με ρεύμα : i = Εεπαγ / Rολ
VΚΛ = VΓΖ = Εεπαγ - i R = iσ Rσ = iκ Rκ => ( iσ Rσ )2 = ( iκ 18 )2 (1)
Pσ = 2 Ρκ => iσ2 Rσ = 2 iκ2 Rκ => iσ2 Rσ = 2 iκ2 18 (2) (1) / (2) => Rσ = 18 / 2 = 9 Ω
Rολ = R + Rσ Rκ / ( Rσ + Rκ ) = 4 + 9 18 / ( 9 + 18 ) = 4 + 6 => Rολ = 10 Ω
Εεπαγ = Β υ l = 2 10 1,5 = 30 V i = Εεπαγ / Rολ = 30 / 10 => i = 3 A
VΚΛ = VΓΖ = 30 - 3 4 = 30 - 12 => VΚΛ = 18 V
iσ = VΚΛ / Rσ = 18 / 9 = 2 A iκ = VΚΛ / Rκ = 18 / 18 = 1 A
Δ2. υ = σταθερή οπότε m g - FL = 0 => m g = B i l => m 10 = 2 3 1,5 => m = 0,9 kg
Δ4. Bσ = 4π 10-7 iσ N / l = 4π 10-7 2 100 = 8π 10-5 Τ
Bκ = 10-7 2π iκ / α = 2π 10-7 1 / 0,5 = 4π 10-7 Τ
Δ5. Qκ = iκ2 Rκ t => 7,2 = 12 18 t => t = 7,2 / 18 = 0,4 sec
h = v t = 10 m/s 0,4 s = 4 m
ΔU = m g h = 0,9 10 4 = 36 J
Qολ = i2 Rολ t = 32 10 0,4 => Qολ = 36 J δηλαδή το έργο που παράγεται από το βάρος της ράβδου (η ταχύτητά της είναι σταθερή) μετατρέπεται σε θερμότητα πάνω στις αντιστάσεις
Δ6. ΣF = m a => m g - FL = m a => m g - B i l = m a => m g - B l Εεπαγ / Rολ = m a =>
=> m g - B l B l v / Rολ = m a => m g - B2 l2 v / Rολ = m a =>
=> 0,9 10 - 22 1,52 v / 10 = 0,9 a => 9 - 0,9 v = 0,9 a => 10 - v = dv/dt =>
=> dv / (v - 10) = - dt => ln [(v - 10) / (-10)] = - t => v - 10 = -10 e-t =>
=> v(t) = 10 - 10 e-t ταχύτητα ράβδου a = dv/dt => a(t) = 10 e-t επιτάχυνση ράβδου
v = dx/dt => dx = v(t) dt => dx = (10 - 10e-t) dt => x(t) = 10t + 10 (e-t - 1)
t = 5 sec e-5 = 0,00674 v = 10 - 0,0674 = 9,933 m/s a = 0,0674 m/s2
x = 50 + 10 (0,00674 - 1) = 50 - 9,933 = 40,0673 m
t = 6 sec e-6 = 0,0025 v = 10 - 0,025 = 9,975 m/s a = 0,025 m/s2
x = 50 + 10 (0,0025 - 1) = 60 - 9,975 = 50,025 m
t = 7 sec e-7 = 0,0009 v = 10 - 0,009 = 9,991 m/s a = 0,009 m/s2
x = 70 + 10 (0,0009 - 1) = 70 - 9,991 = 60,009 m
ΘΕΜΑ 21.
Ομογενής ράβδος ΑΓ μήκους d και μάζας Μ, κρέμεται από άρθρωση και ισορροπεί σχηματίζοντας γωνία φ = 45° με την κατακόρυφο με τη βοήθεια οριζόντιου αβαρούς και μη εκτατού νήματος, το οποίο είναι δεμένο στο κέντρο του ευθύγραμμου αγωγού ΚΛ. Ο αγωγός ΚΛ έχει μήκος ℓ = 0,5 m, μάζα m = 2 kg και αντίσταση R = 0,1 Ω, έχει τα άκρα του σε επαφή με τους οριζόντιους αγωγούς ΔΜ και ΖΝ μεγάλου μήκους και αμελητέας αντίστασης που απέχουν ℓ και ισορροπεί με τη βοήθεια οριζόντιας δύναμης F = 4 Ν που ασκείται κάθετα στον αγωγό και στο κέντρο του, όπως φαίνεται στο σχήμα. Τα άκρα Μ και Ν των οριζόντιων αγωγών συνδέονται μέσω αντίστασης R1 = 0,3 Ω. 
Δ1. Να βρεθεί η μάζα Μ της ράβδου ΑΓ, καθώς και το μέτρο της δύναμης που ασκείται από
την άρθρωση στο άκρο Α της ράβδου.
Τη στιγμή t0 = 0 το νήμα που συγκρατεί τη ράβδο κόβεται και το μέτρο της δύναμης F μεταβάλλεται με τέτοιο τρόπο ώστε ο αγωγός ΚΛ να κινείται με σταθερή επιτάχυνση α=2m/s2 μέσα σε ομογενές μαγνητικό πεδίο, έντασης Β1 = 2 Τ, κατακόρυφης κατεύθυνσης προς τα κάτω.
Δ2. Να βρεθεί η σχέση που συνδέει την δύναμη F που ασκείται στον αγωγό με τον χρόνο
κίνησής του μέσα στο μαγνητικό πεδίο Β1.
Τη στιγμή που η δύναμη F γίνεται ίση με 14 N, ο αγωγός αποκτά ταχύτητα υο και εξέρχεται από το μαγνητικό πεδίο Β1, ενώ ταυτόχρονα καταργείται η δύναμη F. Μετά από λίγο εισέρχεται σε δεύτερο μαγνητικό πεδίο, πλάτους D = 0,4 m, το οποίο έχει ένταση B2 = 0,5 Τ και φορά κατακόρυφη προς τα πάνω.
Δ3. Να βρεθεί ο ρυθμός μεταβολής της κινητικής ενέργειας του αγωγού ΚΛ όταν θα έχει
ταχύτητα υ = υ0 /2 .
Δ4. Να βρεθεί η τάση ΚΛ όταν η ταχύτητα του αγωγού ΚΛ είναι υ = υ0 /2 .
Δ5. Να υπολογιστεί η θερμότητα που δαπανάται στην αντίσταση R του αγωγού ΚΛ κατά την κίνηση του μέσα στο πεδίο Β2 μέχρι να σταματήσει.
Δ1. F = FΓ => FΓ = 4 Ν
Στ(Α) = 0 => Μ g d/2 ημ45° = FΓ d συν45° => Μ g /2 = FΓ => Μ = 2 FΓ / g = 2 4 / 10 = 0,8 kg
FΑx = FΓ = 4 N FΑy = M g = 0,8 10 = 8 N
FΑ2 = FΑx2 + FΑy2 = 42 + 82 = 5 42 => FA = 4 5½ Ν
Δ2. η ράβδος κινείται κόβοντας δυναμικές γραμμές του μαγνητικού πεδίου οπότε τα ηλεκτρόνιά της μετακινούνται προς το άκρο Λ που φορτίζεται αρνητικά ενώ το άκρο Κ φορτίζεται θετικά έτσι αναπτύσσεται τάση εξ' επαγωγής στα άκρα Κ Λ Εεπαγ = Β1 υ l v = a t = 2 t
συνεπώς Εεπαγ = Β1 l a t το κύκλωμα διαρρέεται με ρεύμα εντάσεως i = Εεπαγ / ( R + R1 )
η ράβδος ΚΛ δέχεται δύναμη Laplace FL = B1 i l = B12 l2 a t / (R + R1) = 22 0,52 2 t / (0,1+0,3) = 5t ΣF = m a => F - FL = m a => F - 5t = 2 2 => F = 5t + 4
F = 14 N => 5t + 4 = 14 => t = 2 sec οπότε υ = 2t = 2 2 = 4 m/s = υορ οριακή ταχύτητα
η ράβδος κινείται κόβοντας δυναμικές γραμμές του μαγνητικού πεδίου οπότε τα ηλεκτρόνιά της μετακινούνται προς το άκρο Κ που φορτίζεται αρνητικά ενώ το άκρο Λ φορτίζεται θετικά έτσι αναπτύσσεται τάση εξ' επαγωγής στα άκρα Κ Λ Εεπαγ = Β2 υ D
η ράβδος ΚΛ δέχεται δύναμη Laplace FL = B2 i D = B22 D2 v / (R + R1) = 0,52 0,42 v / 0,4 = 0,1 v
Δ3. ΣF = m a => - FL = m a => - 0,1 v = 2 a => v = -20 a
όταν v = υορ /2 = 4 / 2 = 2 m/s τότε a = - 2/20 = - 0,1 m/s2 επιβράδυνση
dK/dt = m v a = 2kg 2m/s (-0,1m/s2) = - 0,4 J/s
Δ4. Εεπαγ = Β2 υ D i = Εεπαγ / ( R + R1 ) = Β2 υ D / ( R + R1 ) = 0,5 2 0,4 / 0,4 = 1 A VΛΚ = i R1 = 1 A 0,3 Ω => VΛΚ = 0,3 V VΚΛ = -0,3 V
Δ5. Qθερμ = ΔΚ = Κτελ - Καρχ = 0 - ½ m v2 = - ½ 2 42 = - 16 J |Qθερμ|= 16 J
|Qθερμ |= QR + QR1 = 16 J
QR / QR1 = ( i2 R t ) / ( i2 R1 t ) = R / R1 = 0,1 / 0,3 = 1/3
QR / QR1 = 1/3 => QR / (QR + QR1 ) = 1 / (1+3) => QR / 16 J = 1/4 => QR = 4 J 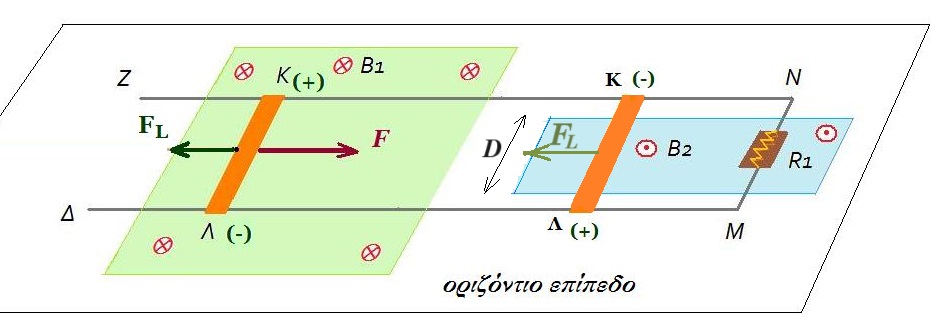
ΘΕΜΑ 22.
Κυκλικός μεταλλικός αγωγός ακτίνας α και ωμικής αντίστασης Rκυκ, συνδέεται σε σειρά με ηλεκτρική συσκευή που έχει χαρακτηριστικά κανονικής λειτουργίας ( Pκ, Vκ ) και ωμική αντίσταση RΣ. Στα άκρα της συνδεσμολογίας τους συνδέουμε ηλεκτρική πηγή και η συσκευή λειτουργεί κανονικά. Το μέτρο της έντασης του μαγνητικού πεδίου στο κέντρο του κυκλικού αγωγού ισούται με B1 .
Στη συνέχεια συνδέουμε τον κυκλικό αγωγό και την ηλεκτρική συσκευή παράλληλα, στα άκρα της συνδεσμολογίας τους συνδέουμε νέα ηλεκτρική πηγή και η συσκευή πάλι λειτουργεί κανονικά. Το μέτρο της έντασης του μαγνητικού πεδίου στο κέντρο του κυκλικού αγωγού τώρα ισούται με Β2. Ο λόγος B1 / B2 ισούται με:
α. Rκυκ /RΣ β. Rκυκ /2RΣ γ. RΣ /Rκυκ
Ρκ = Vκ i Vκ = i RΣ B1 = 10-7 2π i / a = 10-7 2π Vκ / RΣ a
i2 = Vκ / Rκυκ B2 = 10-7 2π i2 / a = 10-7 2π Vκ / Rκυκ a
Β1 / Β2 = Rκυκ / RΣ
ΘΕΜΑ 23.
Δύο λεπτά κατακόρυφα σύρματα Αx και Γy, αμελητέας αντίστασης, είναι στερεωμένα σε μονωμένο οριζόντιο έδαφος. Τα δύο σύρματα έχουν μεγάλο μήκος και είναι παράλληλα μεταξύ τους, έχοντας απόσταση L=1m. Μεταξύ των σημείων Κ και Λ συνδέουμε αντιστάτη, ωμικής αντίστασης R1 = 0,8 Ω. Στο έδαφος στερεώνουμε κατακόρυφα ιδανικό ελατήριο, σταθεράς k=100 N/m. Το φυσικό μήκος του ελατηρίου είναι στο οριζόντιο ευθύγραμμο τμήμα ΗΘ. Σε μία περιοχή υπάρχει οριζόντιο ομογενές μαγνητικό πεδίο, έντασης μέτρου B = 1 T με τις δυναμικές γραμές κάθετες στο επίπεδο των συρμάτων Αx και Γy. Η τομή του μαγνητικού πεδίου με το κατακόρυφο
επίπεδο που ορίζουν οι δύο αγωγοί Αx και Γy είναι το ορθογώνιο παραλληλόγραμμο ΣΤΥΖ, όπου οι πλευρές ΣΤ και ΥΖ είναι οριζόντιες. Η ράβδος ΜΝ έχει μάζα m = 0,5 kg, μήκος L=1m, ωμική αντίσταση R2 = 0,2 Ω και είναι συνεχώς σε επαφή με τα κατακόρυφα σύρματα Αx και Γy. Ανάμεσα στα σημεία Π και Ρ υπάρχει ηλεκτρική πηγή με ΗΕΔ E και εσωτερική αντίσταση r = 0,04 Ω, όπως επίσης και διακόπτης (δ).
Αρχικά ο διακόπτης (δ) είναι κλειστός και η ράβδος ισορροπεί μέσα στο ομογενές μαγνητικό πεδίο.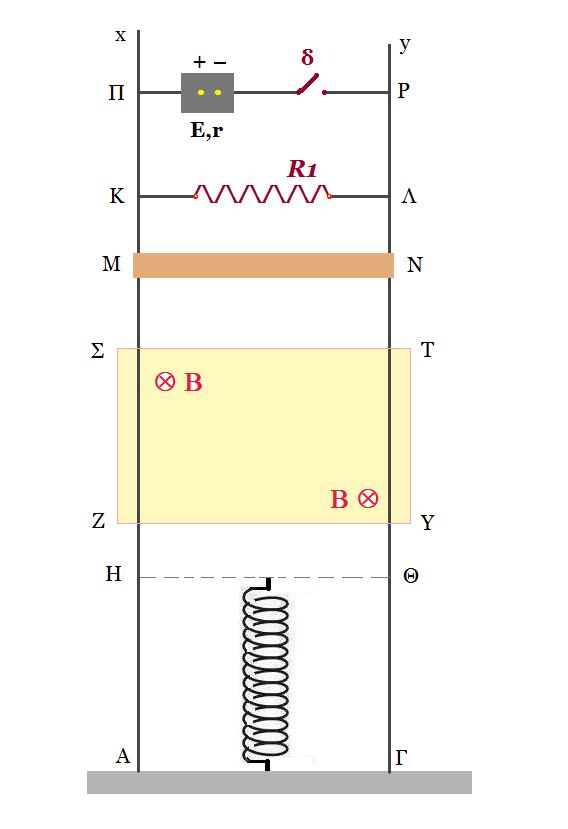 Δ1. Να υπολογίσετε την ΗΕΔ της ηλεκτρικής πηγής.
Δ1. Να υπολογίσετε την ΗΕΔ της ηλεκτρικής πηγής.
Ανοίγουμε τον διακόπτη (δ), ανεβάζουμε τη ράβδο ΜΝ σε ύψος h1 = 0,45 m πάνω από την πλευρά ΣΤ του ομογενούς μαγνητικού πεδίου και την αφήνουμε ελεύθερη. Η ράβδος εισέρχεται στο μαγνητικό πεδίο και έπειτα από λίγο εξέρχεται, έχοντας αποκτήσει οριακή ταχύτητα.
Δ2. Να υπολογίσετε την ένταση του ηλεκτρικού ρεύματος που θα διαρρέει το κύκλωμα, τη στιγμή που η ράβδος ΜΝ εισέρχεται στο μαγνητικό πεδίο.
Δ3. Να υπολογίσετε το μέτρο της οριακής ταχύτητας υορ που θα αποκτήσει η ράβδος ΜΝ μέσα στο ομογενές μαγνητικό πεδίο.
Δ4. Αν το ύψος του μαγνητικού πεδίου είναι (ΣΖ) = (ΤΥ) = h2 = 1 m, να
υπολογίσετε το φορτίο q που μετακινήθηκε στο κύκλωμα, καθώς και το ποσό
θερμότητας Q1 που εκλύθηκε από την αντίσταση R1, από τη στιγμή που η ράβδος εισήλθε μέχρι τη στιγμή που εξήλθε από το μαγνητικό πεδίο.
Δ5. Όταν η ράβδος ΜΝ εξέρχεται από το ομογενές μαγνητικό πεδίο, βρίσκεται σε ύψος h3 πάνω από το φυσικό μήκος του ελατηρίου. Η ράβδος καρφώνεται στο ελατήριο και αρχίζει να εκτελεί απλή αρμονική ταλάντωση, με σταθερά επαναφοράς D = k. Αν γνωρίζετε ότι το πλάτος της ταλάντωσης είναι Α = 9/20 m, να υπολογίσετε το ύψος h3.
Δ1. ισοοροπία ράβδου ΜΝ : m g = FL = B i2 l => 0,5 10 = 1 i2 1 => i2 = 5 A
VMN = i2 R2 = 5 A 0,2 Ω = 1 Volt
VΚΛ = i1 R1 => 1 V = i1 0,8 Ω => i1 = 1,25 A = 5/4 A i = i1 + i2 = 6,25 A
E = i { r + R1 R2 / ( R1 + R2 ) } = 6,25 { 0,04 + 0,2 0,8 / ( 0,2 + 0,8 ) } = 6,25 0,2 = 1,25 V
Δ2. h = ½ g t2 => 0,45 = ½ 10 t2 => t2 = 0,09 => t = 0,3 s v = g t = 10 0,3 = 3 m/s
η ράβδος ΜΝ μόλις εισέρχεται στο μαγνητικό πεδίο έχει ταχύτητα 3 m/s στα άκρα της θα αναπτυχθεί επαγωγική τάση Εεπαγ = Β υ l = 1 3 1 = 3 V με πολικότητα Μ(-) και Ν(+) τότε
Εεπαγ = i ( R1 + R2 ) => 3 = i 1 => i = 3 A
Δ3. Εεπαγ = Β υ l το κύκλωμα διαρρέεται με ρεύμα εντάσεως i = Εεπαγ / ( R1 + R2 )
η ράβδος MN δέχεται δύναμη Laplace FL = B i l = B2 l2 v / (R1 + R2) = 12 12 v / 1 = v
ΣF = m a => m g - FL = m a => 0,5 10 - v = 0,5 a => 5 - v = 0,5 a όταν α = 0 τότε υορ = 5 m/s οριακή ταχύτητα εξόδου
Δ4. q = ΔΦ / R = B A / R = 1 1 / 1 = 1 C
Καρχ + m g h2 = Κτελ + Qθερμ => ½ 0,5 32 + 0,5 10 1 = ½ 0,5 52 + Qθερμ =>
=> 9/4 + 5 = 25/4 + Qθερμ => 9/4 + 5 - 25/4 = Qθερμ => Qθερμ = - 1 J
|Qθερμ |= QR1 + QR2 = 1 J
QR1 / QR2 = ( i2 R1 t ) / ( i2 R2 t ) = R1 / R2 = 0,8 / 0,2 = 4
QR1 / QR2 = 4 => QR1 / (QR1 + QR2 ) = 4 / (4+1) => QR1 / 1 J = 4/5 => QR = 4/5 J = 0,8 J
Δ5. θέση ισορροπίας : m g = k x0 => 0,5 10 = 100 x0 => x0 = 0,05 m
Καρχ + m g h3 = Κτελ => ½ 0,5 52 + 0,5 10 h3 = ½ 0,5 v2 => 52 + 20 h3 = v2
για την ταλάντωση
½ k x02 + ½ m v2 = ½ k A2 => ½ 100 (1/20)2 + ½ 0,5 v2 = ½ 100 (9/20)2 =>
=> 100 1/400 + 0,5 v2 = 100 81/400 => 1/4 + 0,5 v2 = 81/4 =>
=> 0,5 v2 = 80/4 = 20 => v2 = 40
οπότε από την σχέση 52 + 20 h3 = v2 = 40 => 25 + 20 h3 = 40 => 20 h3 = 40 - 25 = 15 => h3 = 15/20 = 0,75 m
ΘΕΜΑ 24.
Οριζόντιος ευθύγραμμος αγωγός ΚΛ μήκους L=1m, μάζας m και ωμικής αντίστασης R=20Ω
μπορεί να ολισθαίνει χωρίς τριβές παραμένοντας οριζόντιος και εφαπτόμενος στους δύο
κατακόρυφους στύλους ΑΓ και ΔΖ που απέχουν απόσταση L. Τα επάνω άκρα Α και Δ των
δύο στύλων είναι συνδεδεμένα με λαμπτήρα που έχει στοιχεία κανονικής λειτουργίας
80W-40V. Τα κάτω άκρα Γ και Ζ των στύλων, είναι συνδεδεμένα μέσω διακόπτη με πηγή
ΗΕΔ Ε=24V και εσωτερική αντίσταση r=2Ω. Η όλη διάταξη βρίσκεται μέσα σε οριζόντιο
ομογενές μαγνητικό πεδίο έντασης Β=1Τ. Αρχικά κρατάμε ακίνητο τον αγωγό και την χρονική στιγμή t=0 κλείνουμε τον
Αρχικά κρατάμε ακίνητο τον αγωγό και την χρονική στιγμή t=0 κλείνουμε τον
διακόπτη δ, αφήνοντας ελεύθερο τον αγωγό και διαπιστώνουμε ότι ισορροπεί ακίνητος.
Δ1. Να υπολογίσετε την ένταση Ι του ρεύματος που διαρρέει την πηγή.
Δ2. Να εξετάσετε αν ο λαμπτήρας λειτουργεί κανονικά.
Δ3. Να υπολογίσετε τη μάζα του αγωγού και τη θερμότητα που εκλύεται στον αγωγό σε
χρόνο Δt=100sec.
Δ4. Τη χρονική στιγμή t=0 αντιστρέφουμε την φορά της έντασης του μαγνητικού πεδίου
και ασκούμε στον αγωγό κατακόρυφη δύναμη F=3N με φορά προς τα πάνω. Προς ποια
κατεύθυνση θα κινηθεί ο αγωγός και ποιο το μέτρο της επιτάχυνσής του τη χρονική στιγμή
t=0;
λαμπτήρας P = V2 / Rλ => Rλ = 402 / 80 = 20 Ω
E = i { r + R Rλ / ( R + Rλ ) } => 24 = i { 2 + 20 20 / ( 20 + 20 ) } => i = 2 A
Vπολ = Ε - i r = 24 - 2 2 = 20 V iΚΛ = Vπολ / R = 20 / 20 = 1 Α iλ = 1 Α
Vλ = iλ Rλ = 1 20 = 20 V < 40 V ο λαμπτήρας υπολειτουργεί
ισορροπία ράβδου m g = FL = B iΚΛ l => m 10 = 1 1 1 => m = 0,1 kg
Qθερμ = iΚΛ 2 R t = 1 20 100 = 2000 Watt
ΣF = m a => F - m g - FL = m a => 3 - 1 -1 = 0,1 a => 3 - 1 - 1 = 0,1 a => a = 10 m/s2 επιτάχυνση κατακόρυφη προς τα πάνω
ΘΕΜΑ 25.
Ένα τετράγωνο αγώγιμο πλαίσιο πλευράς α=20cm αποτελείται από Ν=50 σπείρες και εμφανίζει ωμική αντίσταση Rπ=2Ω. Το πλαίσιο περιστρέφεται με σταθερή συχνότητα 5Hz γύρω από άξονα ο οποίος διέρχεται από τα μέσα δύο απέναντι πλευρών του.
Ολόκληρο το πλαίσιο βρίσκεται μέσα σε oμογενές μαγνητικό πεδίο έντασης μέτρου Β=2Τ του οποίου οι μαγνητικές γραμμές είναι κάθετες στον άξονα περιστροφής και το διάνυσμα που προσανατολίζει την επιφάνεια του πλαισίου τη χρονική στιγμή t=0 σχηματίζει γωνία μηδέν μοίρες με τις δυναμικές γραμμές. Στα άκρα του πλαισίου έχει συνδεθεί αντιστάτης με αντίσταση R=8Ω. Δίνεται π2=10.
Γ1. Να σχεδιάσετε τη γραφική παράσταση της μαγνητικής ροής που διέρχεται από μία σπείρα του πλαισίου σε συνάρτηση με τον χρόνο.
Γ2. Να γράψετε τη χρονική εξίσωση της έντασης του εναλλασσόμενου ρεύματος που διαρρέει τον αντιστάτη.
Γ3. Να υπολογίσετε την ενέργεια που εκλύεται από τον αντιστάτη με την μορφή
θερμότητας, λόγω του φαινομένου joule, σε χρόνο μισής περιόδου της εναλλασσόμενης τάσης.
Γ4. Να υπολογίσετε την τάση που επικρατεί στα άκρα του αντιστάτη τη χρονική στιγμή t=1/20sec.
συχνότητα 5 Ηz περίοδος Τ = 1/f = 1/5 s = 0,2 s
εμβαδόν επιφάνειας πλαισίου : Α = α2 = 0,22 m2 = 0,04 m2
μαγνητική ροή (συνολική) : Φ = Β Α Ν συν2πft = 2 0,04 50 συν(2 π 5 t) = 4 συν10πt
μέγιστη τιμή εναλλασσομένης τάσης : V0 = 2πf B A N = 10π 2 0,04 50 = 40π Volt
V(t) = V0 ημωt = 40π ημ10πt = Εεπαγ επαγωγική τάση στα άκρα του πλαισίου
νόμος του Ohm για κλειστό κύκλωμα : Εεπαγ = i (R + Rπ) =>
=> 40π ημ10πt = i (2+8) => i(t) = 4π ημ10πt
P = i2 R = 16π2 ημ210πt 8 => P(t) = 1280 ημ210πt
μέγιστη ισχύς : Ρ0 = 1280 Watt μέση ισχύς : ΡΜ = Ρ0 / 2 = 640 Watt
σε χρόνο μισής περιόδου ο αντιστάτης καταναλώνει ενέργεια 640 W 0,1 s = 64 J
i(1/20) = 4π ημ(10π 1/20) = 4π ημ(π/2) = 4π A VR = i R = 4π A 8Ω = 32π Volt
ΘΕΜΑ 26.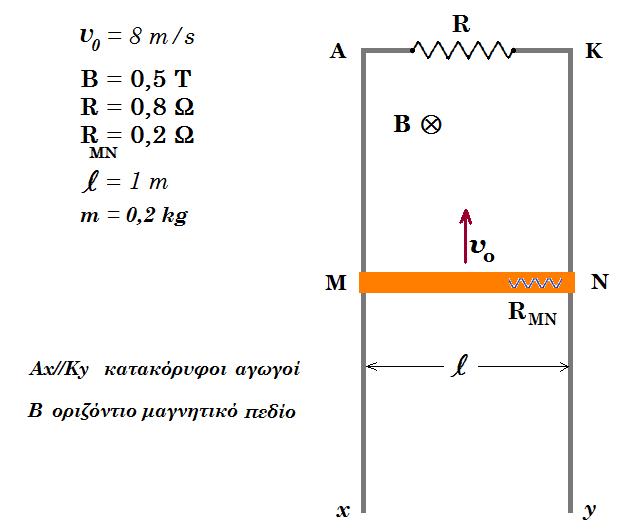
Θεωρούμε την διάταξη του σχήματος. Την χρονική στιγμή t0 = 0 εκτοξεύουμε την ράβδο προς τα πάνω με αρχική ταχύτητα υ0 = 8 m/s. Μεταξύ της ραβδου και των αγωγών Ax, Ky υπάρχει συνολική δύναμη τριβής Τ = 1 Ν. Να μελετηθεί η κίνηση της ράβδου. Υπολογίστε την αρχική επιτάχυνση της ράβδου.
Κάποια στιγμή t1 μηδενίζεται η ταχύτητα της ράβδου. Έστω ότι η ράβδος έχει διανύσει κατακόρυφη προς τα πάνω απόσταση h = 1,2 m από τη στιγμή t0 έως τη στιγμή t1. Υπολογίστε το ποσό της θερμότητας που αναπτύσσεται στις αντιστάσεις.
Ακολούθως η ράβδος κινείται λόγω βαρύτητας προς τα κάτω. Μελετήστε την κίνηση της ράβδου.
Υπολογίστε την τάση VMN στα άκρα της ράβδου μετά από πολύ χρόνο.
Να συγκρίνετε τον ρυθμό μεταβολής του έργου της δύναμης της τριβής με τον ρυθμό μεταβολής του έργου της δύναμης της Laplace.
Αν η ταχύτητα της ράβδου μεταβάλλεται με τον χρόνο σύμφωνα με την σχέση: v(t) = 4 - 4e-5/4t
βρείτε τον ρυθμό μεταβολής του έργου της τριβής καθώς και της δύναμης Laplace.
θετική φορά προς τα πάνω όπως κινείται η ράβδος
Εεπαγ = B v l Εεπαγ = i ( R + RMN ) => i = B v l / ( R + RMN )
FL = B i l = B2 l2 v /( R + RMN ) => FL = 0,52 12 v /( 0,8 + 0,2 ) => FL = v/4
ΣF = - m g - T - FL = m a => - 0,2 10 - 1 - v/4 = 0,2 a => - 3 - v/4 = 0,2 a => a = -15 - 5v/4
αρχική ταχύτητα υ0 = 8 m/s τότε αρχική επιτάχυνση α = - 15 - 5 8 / 4 = -25m/s2 (επιβράδυνση)
κάποια στιγμή η ράβδος θα σταματήσει στιγμιαία και θα κινηθεί προς τα κάτω λόγω βαρύτητας
διατήρηση ενέργειας : ½ m v02 = m g h + T h + WFL =>
=> ½ 0,2 82 = 0,2 10 1,2 + 1 1,2 + WFL =>
=> 6,4 = 2,4 + 1,2 + WFL => WFL = 2,8 J = Qθερμ
--------------------------------------------------------------------------------------------------
η ράβδος κινείται προς τα κάτω
Εεπαγ = B v l Εεπαγ = i ( R + RMN ) => i = B v l / ( R + RMN )
FL = B i l = B2 l2 v /( R + RMN ) => FL = 0,52 12 v /( 0,8 + 0,2 ) => FL = v/4
ΣF = m g - T - FL = m a => 0,2 10 - 1 - v/4 = 0,2 a => 1 - v/4 = 0,2 a => a = 5 - 5v/4 η ταχύτητα αυξάνεται οπότε η επιτάχυνση μειώνεται μέχρι να μηδενισθεί
α = 0 => υ = 4m/s = υορ οριακή ταχύτητα τότε Εεπαγ = B vορ l = 0,5 4 1 = 2 Volt
i = Εεπαγ /( R + RMN ) = 2V / 1Ω = 2Α VNM = i R = 2A 0,8Ω = 1,6V VMN = - 1,6V
ΡΤ = Τ υορ = 1Ν 4m/s = 4 J/s
ΡFL = FL υορ = υορ /4 υορ = 4/4 4 = 4 J/s παρατηρούμε ότι ΡΤ = ΡFL = 4 J/s
ρυθμός μεταβολής δυναμικής ενέργειας dU/dt = - m g υορ = - 0,2kg 10m/s2 4m/s = - 8 J/s
--------------------------------------------------------------------------------------------------------
a = 5 - 5v/4 => dv/dt = - 5/4 (v - 4) => dv / (v - 4) = - 5/4 dt =>
=> ln [(v - 4) / (-4)] = - 5/4 t => v(t) = 4 - 4 e-5/4 t a(t) = 5/4 e-5/4 t
v = dx/dt => dx = v dt = [ 4 - 4 e-5/4 t ] dt => x(t) = 4 t + 16/5 [ e-5/4 t - 1 ]
ΡΤ = Τ υ = 1 Ν { 4 - 4 e-5/4 t } = 4 - 4 e-5/4 t = 4 { 1 - e-5/4 t }
ΡFL = FL υ = υ/4 υ = υ2 / 4 = { 4 - 4 e-5/4 t }2 / 4 = 4 { 1 - e-5/4 t }2
μετά από πολύ χρόνο ( t > 4 s ) παρατηρούμε ότι : ΡΤ = ΡFL = 4 J/s

ΘΕΜΑ 27.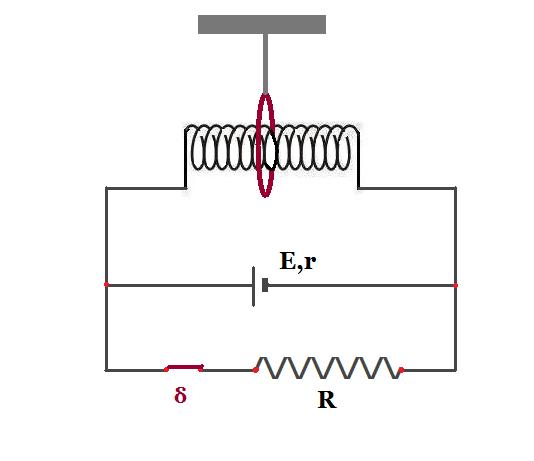
Σωληνοειδές μήκους l αποτελείται από Ν σπείρες, ακτίνας α η καθεμιά, έχει αντίσταση R και συνδέεται με ηλεκτρική πηγή που έχει ηλεκτρεγερτική δύναμη Ε και εσωτερική αντίσταση r=R/2. Στους πόλους της πηγής είναι συνδεδεμένος μέσω διακόπτη (δ), αντιστάτης με αντίσταση R. Ο διακόπτης αρχικά είναι κλειστός. Γύρω από το σωληνοειδές, στο κέντρο του, έχουμε τοποθετήσει έναν κυκλικό αγωγό, μιας σπείρας, με το επίπεδό του κάθετο στον άξονα του σωληνοειδούς όπως φαίνεται στο σχήμα. Ο κυκλικός αγωγός έχει ακτίνα 2α, αντίσταση R και είναι κρεμασμένος μέσω μονωτικής σταθερής ράβδου που είναι συνδεμένη σε ακλόνητο σημείο. Θεωρούμε ότι το μαγνητικό πεδίο του σωληνοειδούς είναι αμελητέο στο εξωτερικό του στην περιοχή όπου βρίσκεται ο κυκλικός αγωγός.
Κάποια στιγμή ανοίγουμε το διακόπτη. Το επαγωγικό φορτίο που μετατοπίζεται στον κυκλικό αγωγό θα είναι:
i) 16/3 π2 α2 kμ N/l E/R2 ii) 8/3 π2 α2 kμ N/l E/R2 iii) 2/3 π2 α2 kμ N/l E/R2
Ε = i ( R/2 + R R / (R+R) ) = i ( R/2 + R/2 ) = i R => i = E / R
i1 = E / 2R Β1 = 4π kμ i1 N/l A = π α2
Φ1 = Β1 Α = 4π kμ E/2R N/l π α2
i2 = E / (R + R/2) = 2E / 3R
Φ2 = Β2 Α = 4π kμ 2E/3R N/l π α2
i2 - i1 = 2E/3R - E/2R = Ε / 6R
Q = ( Φ2 - Φ1 ) / R = 4π kμ E/6R N/l π α2 / R = 2/3 π2 α2 kμ N/l E/R2
ΘΕΜΑ 28.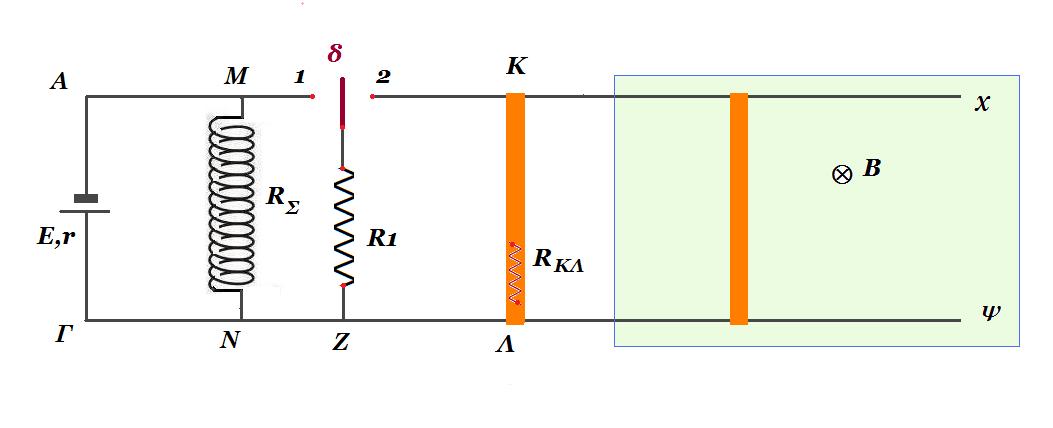
Οι οριζόντιοι μεταλλικοί αγωγοί Αχ και Γψ έχουν μεγάλο μήκος, σταθερή την μεταξύ τους απόσταση και αμελητέα ωμική αντίσταση. Στη διάταξη του σχήματος, αρχικά ο διακόπτης (μεταγωγός) δ βρίσκεται στη θέση 1. Η πηγή έχει ΗΕΔ 𝛦 = 1,5𝑉 και εσωτερική αντίσταση 𝑟 = 0,5𝛺. Το κύκλωμα περιλαμβάνει αντιστάτη συνδεδεμένο παράλληλα με το σωληνοειδές ωμικής αντίστασης 𝑅1 = 5 𝛺. Για το σωληνοειδές δίνονται, η ωμική του αντίσταση 𝑅𝛴 = 5 𝛺, το μήκος του 𝐿 = 0,5 𝑚 και ο αριθμός των σπειρών του Ν=1000 σπείρες.
Γ1. Υπολογίστε το μέτρο της έντασης του μαγνητικού πεδίου στο μέσο του σωληνοειδούς.
Στη συνέχεια ο διακόπτης μεταφέρεται ακαριαία και χωρίς να δημιουργηθεί σπινθήρας στη θέση 2 και η αγώγιμη ράβδος ΚΛ εκτοξεύεται με αρχική ταχύτητα παράλληλη προς τους αγωγούς Αx και Γψ οπότε εισέρχεται σε περιοχή ομογενούς μαγνητικού πεδίου (σκιασμένη περιοχή) μαγνητικής επαγωγής 𝛣 = 2 𝛵 κάθετης στο επίπεδο των αγωγών. Τη στιγμή της εισόδου της, 𝑡0 = 0 𝑠 κινείται με ταχύτητα v0 = 1𝑚/𝑠 παράλληλη στην διεύθυνση των αγωγών Αχ και Γψ, ενώ πάνω της αρχίζει να ασκείται εξωτερική δύναμη μέτρου Fεξ ομόρροπη προς την ταχύτητα της, με αποτέλεσμα να κινείται με σταθερή επιτάχυνση 𝑎=0,25𝑚/𝑠2.
Η αγώγιμη ράβδος ΚΛ έχει μήκος 𝑙 = 0,5 𝑚, μάζα 𝑚=0,4𝐾𝑔, ωμικής αντίστασης 𝑅𝛫𝛬=5𝛺 και μπορεί να ολισθαίνει, χωρίς τριβές, στους οριζόντιους αγωγούς Αχ και Γψ παραμένοντας διαρκώς κάθετη σε αυτούς.
Γ2. Υπολογίστε το φορτίο που περνάει από την αγώγιμη ράβδο από τη στιγμή t0=0 μέχρι τη στιγμή t1=4s.
Γ3. Τη χρονική στιγμή 𝑡1 η τιμή της εξωτερικής δύναμης σταθεροποιείται, στην τιμή που έχει εκείνη τη στιγμή. Περιγράψτε το είδος της κίνησης του αγωγού ΚΛ, από τη στιγμή 𝑡1 μέχρι να αποκτήσει σταθερή ταχύτητα.
Γ4. Υπολογίστε την ισχύ της εξωτερικής δύναμης όταν ο αγωγός κινείται με σταθερή ταχύτητα.
Γ1. RΣ,1 = RΣ R1 / (RΣ + R1) = 5 5 / (5+5) = 2,5 Ω
νόμος του Ohm : Ε = i (r + RΣ,1) => i = Ε / (r + RΣ,1) = 1,5 / (0,5 + 2,5) = 1,5 / 3 => i = 0,5 Α ΒΣ = 4π 10-7 i Ν/𝐿 = 4π 10-7 0,5 1000/0,5 => ΒΣ = π 10-4 Τ
Γ2. v = v0 + a t => v = 1 + 0,25 t Eεπαγ = Β l v = 2 0,5 (1 + 0,25 t) = 1 + 0,25 t
FL = B l i = B l Eεπαγ / (RΚΛ + R1) = 2 0,5 (1 + 0,25 t) / (5 + 5) => FL = 0,1 + 0,025t
ΣF = m a => Fεξ - FL = m a => Fεξ - (0,1 + 0,025t) = 0,4𝐾𝑔 0,25𝑚/𝑠2 =>
=> Fεξ = 0,1 + 0,025 t + 0,1 => Fεξ(t) = 0,2 + 0,025 t
i(t) = Eεπαγ / (RΚΛ + R1) => i(t) = 0,1 + 0,025 t i(0) = 0,1 Α,
i(4) = 0,1 + 0,025 4 = 0,1 + 0,1 = 0,2 Α q = (0,1 + 0,2) 4 / 2 C => q = 0,6 C
Γ3. Fεξ(4) = 0,2 + 0,025 4 = 0,2 + 0,1 = 0,3 Ν v = 1 + 0,25 t = 1 + 0,25 4 = 2 m/s
ΣF = m a => Fεξ - FL = m a => Fεξ - B2 l2 υ /(RΚΛ + R1) = m a => 0,3 - υ/10 = 0,4 a =>
=> 3 - υ = 4 a => - (v - 3) = 4 dv/dt => dv / (v - 3) = - dt / 4 => ln [ (v-3) / (2-3) ] = - t/4 => => v - 3 = - e-t/4 => v(t) = 3 - e-t/4 v(0) = 3 - 1 = 2m/s v(¥) = 3m/s = υορ οριακή ταχύτητα
α(t) = 1/4 e-t/4 α(0) = 1/4 = 0,25 m/s2 α(¥) = 0
Γ4. ΡFεξ = Fεξ υ = 0,3 Ν 3 m/s = 0,9 J/s
i = Eεπαγ / (RΚΛ + R1) = B l υ / (RΚΛ + R1) = 2 0,5 3 / 10 = 0,3 A
FL = B l i = 2 0,5 0,3 = 0,3 N = Fεξ
Pθερμ = i2 (RΚΛ + R1) = 0,32 10 = 0,9 Watt
ΘΕΜΑ 29.
Oριζόντιος αγωγός ΚΛ, έχει μήκος l=1m, μάζα m=0,8Kg και αντίσταση R=0,2Ω. Ο Αγωγός μπορεί και ολισθαίνει , χωρίς τριβές, σε κατακόρυφο επίπεδο στηριζόμενους στους αγωγούς Αx και Γy οι οποίοι έχουν αμελητέα αντίσταση και μεγάλο μήκος. Τα άκρα Α Γ των αγωγών συνδέονται με αντιστάτη αντίστασης R1=0,8Ω. Ο αγωγός ΚΛ κινείται προς τα πάνω, υπό την επίδραση δύναμης F, έχοντας σταθερή ταχύτητα υ=4m/s. Όλη η διάταξη βρίσκεται σε ομογενές οριζόντιο μαγνητικό πεδίο έντασης Β=1Τ.
Γ1) Υπολογίστε το μέτρο της δύναμης F.
Κάποια στιγμή η δύναμη F καταργείται.
Γ2) Να χαρακτηρίσετε την κίνηση του αγωγού ΚΛ κατά την άνοδο του (μετά τη κατάργηση της F) και να βρείτε την ένταση του ρεύματος όταν η δύναμη που δέχεται ο αγωγός έχει μέτρο FL = mg/4 ενώ ο αγωγός συνεχίζει να κινείται προς τα πάνω.
Γ3) Υπολογίστε την σταθερή ταχύτητα που αποκτά (οριακή) ο αγωγός κατά την κάθοδο του.
Γ1. καθώς κινείται η ράβδος προς τα πάνω μέσα στο μαγνητικό πεδίο τα ηλεκτρόνιά της δέχονται δύναμη Lorenz και κινούνται προς το άκρο Λ που φορτίζεται αρνητικά ενώ το άκρο Κ φορτίζεται θετικά, έτσι αναπτύσσεται τάση στα άκρα Κ, Λ : Εεπαγ = Β l v = 1T 1m v = v = 4 V το κύκλωμα διαρρέεται με ρεύμα εντάσεως : i = Εεπαγ / (R1 + R) = v / (0,8 + 0,2) = v = 4 A η ράβδος διαρρέεται με ρεύμα και κινείται μέσα στο μαγνητικό πεδίο συνεπώς δέχεται δύναμη Laplace FL=B i l = 1T v 1m = v = 4 N
ΣF = m a = 0 διότι η ταχύτητα της ράβδου είναι σταθερή v = 4 m/s οπότε : F - m g - FL = 0 => F - 0,8 10 - 4 = 0 => F = 12 Ν
Γ2. η ράβδος ανέρχεται, η δύναμη F καταργείται, Εεπαγ = Β l v,
i = Εεπαγ / (R1 + R) = Β l v / (R1 + R), FL = B i l = B2 l2 υ / (R1 + R)
ΣF = m a => - m g - FL = m a => - m g - Β2 l2 v / (R1 + R) = m a =>
=> - 0,8 10 - 12 12 v / (0,8 + 0,2) = 0,8 a => - 8 - v = 0,8 a => - 10 - 5/4 v = a , μετά την κατάργηση της δύναμης F, η ράβδος επιβραδύνεται καθώς ανέρχεται, αρχικά όταν υ = 4m/s τότε α = - 10 - 5 = - 15 m/s2 , κάποια στιγμή η ταχύτητα μηδενίζεται τότε α = - 8 m/s2 , μετά η ράβδος θα κινηθεί κατακόρυφα προς τα κάτω
όταν FL = mg/4 τότε - m g - FL = m a => - m g - mg/4 = m a => - 5g/4 = a => α = -12,5m/s2
FL = Β2 l2 v / (R1 + R) => mg/4 = Β2 l2 v / (R1 + R) =>
=> 0,8 10 / 4 = 12 12 v / (0,8 + 0,2) => v = 2 m/s
FL = mg/4 => Β i l = mg/4 => 1 i 1 = 0,8 10 / 4 => i = 2 A
Γ3. η ράβδος κατέρχεται ΣF = m a => m g - FL = m a => m g - Β2 l2 v / (R1 + R) = m a => 8 - 12 12 v / 1 = 0,8 a => 8 - v = 0,8 a => 10 - 5/4 v = a η ταχύτητα υ αυξάνεται η επιτάχυνση μειώνεται μέχρι τη στιγμή που θα μηδενισθεί, έχουμε α = 0 => v = 8 m/s οριακή ταχύτητα (σταθερή)
ΘΕΜΑ 30.
Η ράβδος ΚΛ στο ακόλουθο σχήμα ισορροπεί. Διαρρέεται με ρεύμα i1 , δέχεται δυνάμεις από τα ιδανικά ελατήρια και από τον ευθύγραμμο ρευματοφόρο αγωγό. Τα ελατήρια συνδέονται με την ράβδο από το ένα άκρο τους και με ακλόνητο τοίχο από το άλλο άκρο.

Η μετατόπιση x της ράβδου είναι πολύ μικρότερη της απόστασης d ( x << d ).
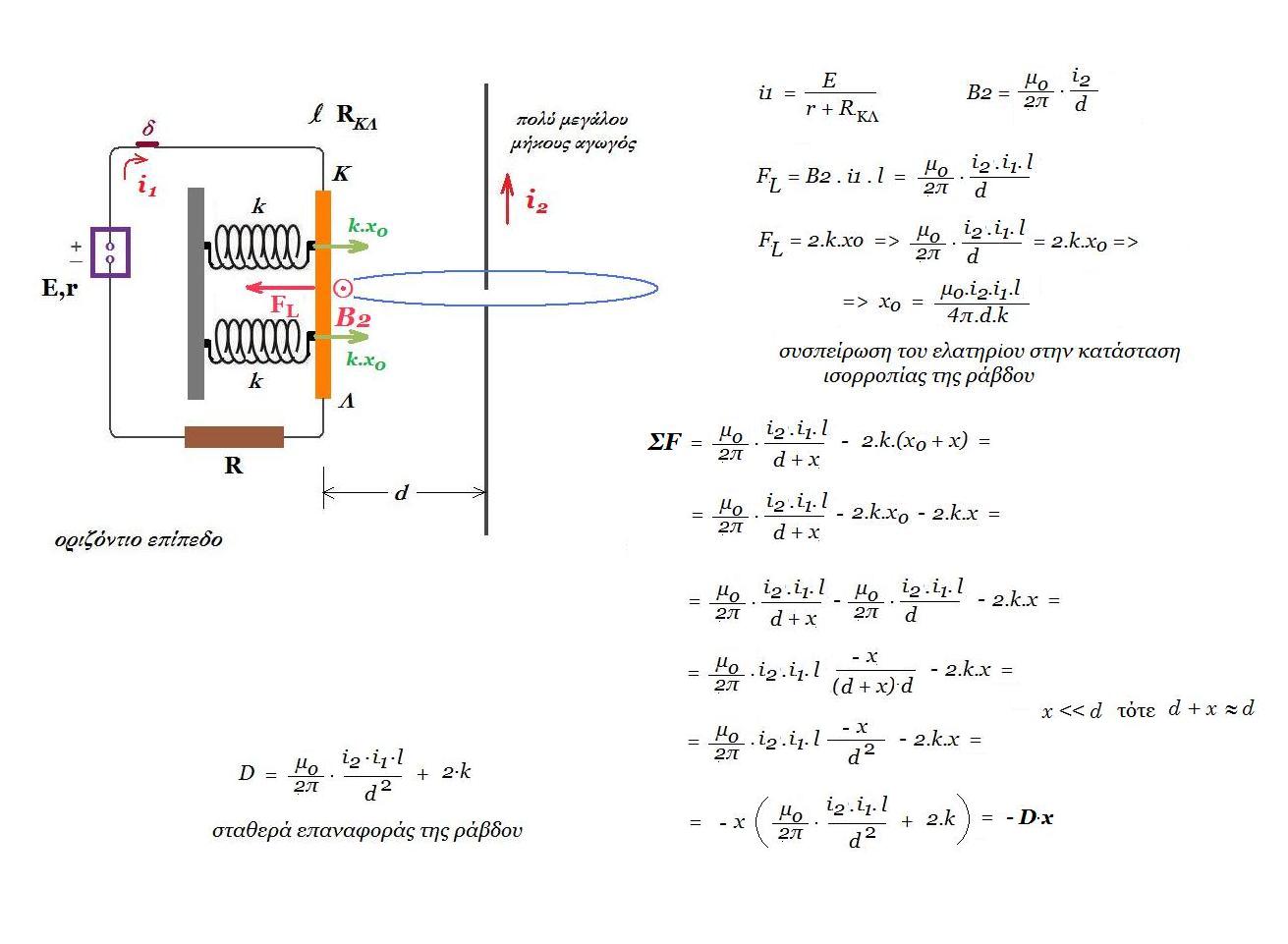
l = 2 m d = 2 10-2 m x0 = 10-3 m i2 = 10 A k = 1 N/m
E = 10 V r = 0,1 Ω R = 0,5 Ω RΚΛ = 0,4 Ω
i1 = E / ( r + R + RΚΛ ) i1 = 10 / ( 0,1 + 0,5 + 0,4 ) Β2 = 10(-7) 2 i2 / d
FL = B2 i1 l = 10(-7) 2 i2 i1 l / d
ισορροπία ράβδου : ΣF = 0 => FL = Fελατ => 10-7 2 i2 i1 l / d = 2 k x0 =>
=> 10(-7) i2 i1 l / d = k x0 => 10-7 i2 i1 2 / (2 10-2) = k 10-3 =>
=> 10-7 i2 i1 = k 10-5 => 10-2 10 10 = 1
ΘΕΜΑ 31. θέμα Γ 2021
Στο σχήμα οι αγωγοί ΑΓ, ΔΖ, μεγάλου μήκους, βρίσκονται στο ίδιο οριζόντιο επίπεδο, είναι παράλληλοι μεταξύ τους, απέχουν l = 1 m και έχουν μηδενική ωμική αντίσταση. Η ράβδος ΚΛ έχει μήκος l = 1 m μάζα m = 0,5 kg, αντίσταση RΚΛ = 2 Ω και αρχικά είναι ακίνητη. Η ράβδος ΚΛ μπορεί να κινείται χωρίς τριβές, παραμένοντας συνεχώς κάθετη και σε επαφή με τους αγωγούς ΑΓ, ΔΖ.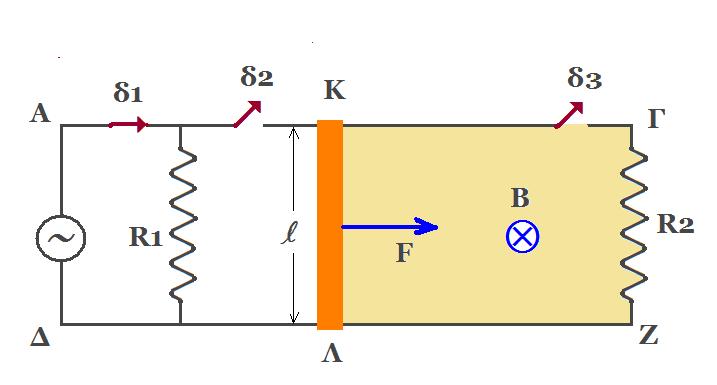
Η γεννήτρια εναλλασσόμενου ρεύματος που συνδέεται στα άκρα Α,Δ περιέχει αγώγιμο πλαίσιο μηδενικής αντίστασης , το οποίο στρέφεται με σταθερή γωνιακή ταχύτητα ω γύρω από άξονα που βρίσκεται στο επίπεδό του και είναι κάθετος στις δυναμικές γραμμές ομογενούς μαγνητικού πεδίου. Η χρονική εξίσωση της στιγμιαίας τιμής της εναλλασσόμενης τάσης που εμφανίζεται στο πλαίσιο είναι V = V0 ημ(50πt) S.I. Οι αντιστάτες που φαίνονται στο σχήμα έχουν τιμές R1 = 6Ω και R2 = 3Ω. Από την αρχική θέση της ράβδου ΚΛ και στον χώρο δεξιά απ’ αυτήν, υπάρχει κατακόρυφο ομογενές μαγνητικό πεδίο έντασης B, του οποίου οι δυναμικές γραμμές έχουν διεύθυνση κάθετη στο επίπεδο της σελίδας και φορά από τον αναγνώστη προς αυτήν, όπως φαίνεται στο σχήμα και καλύπτει όλη τη γραμμοσκιασμένη περιοχή.
Γ1. Αρχικά, ο διακόπτης δ1 είναι κλειστός και οι δ2 , δ3 είναι ανοικτοί. Τότε, η μέση ισχύς στον αντιστάτη R1 ισούται με 12W. Υπολογίστε το πλάτος της τάσης V και την ενεργό ένταση του ρεύματος στον αντιστάτη R1.
Γ2. Διατηρώντας τον διακόπτη δ1 κλειστό και ανοιχτούς τους διακόπτες δ2 και δ3, διπλασιάζουμε τη συχνότητα περιστροφής του πλαισίου στη γεννήτρια εναλλασσόμενης τάσης. Η στιγμιαία τιμή της τάσης που παράγεται τότε χει τη μορφή υ’ = V’·ημ(ω’t). Να γραφεί η χρονική εξίσωση της στιγμιαίας ισχύος στον αντιστάτη R1 και να υπολογιστεί η τιμή της τη χρονική στιγμή 5·10-3 sec.
Γ3. Τη χρονική στιγμή t0=0, ανοίγουμε τον διακόπτη δ1 και ασκούμε στο μέσο της ράβδου ΚΛ σταθερή οριζόντια δύναμη, κάθετη στη ράβδο μέτρου F=0,5N με φορά, όπως στο σχήμα. Τη στιγμή 2sec κλείνουμε τους διακόπτες δ2 και δ3 και παρατηρούμε ότι έκτοτε η ράβδος κινείται με σταθερή ταχύτητα. Υπολογίστε το μέτρο της έντασης B του μαγνητικού πεδίου μέσα στο οποίο κινείται η ράβδος.
Γ4. Για το χρονικό διάστημα 0 έως 5sec, να υπολογίσετε το ποσοστό επί τοις εκατό του έργου της F που μετατρέπεται σε θερμότητα στον αντιστάτη R2.
Γ1.
P = V2 / R1 => V2 = P R1 = 12 6 = 72 => Vεν = 6 2½ Volt V0 = 6 2½ 2½ Volt = 12 V
Ιεν = Vεν / R1 = 6 2½ / 6 = 2½ Α
Γ2.
εφ' όσον διπλασιάζουμε την συχνότητα περιστροφής του πλαισίου θα διπλασιασθεί το πλάτος της εναλλασσόμενης τάσης δηλαδή θα γίνει 24 V
P = V2 / R1 = 242 ημ2(100πt) / 6 => P(t) = 96 ημ2(100πt)
P(0,005) = 96 ημ2(100π 0,005) = 96 ημ2(π/2) = 96 Watt
Γ3.
ΣF = m a => F = m a => a = 0,5 N / 0,5 kg = 1 m/s2 v = a t = 1 m/s2 2 s = 2 m/s
η ράβδος ΚΛ έχει αποκτήσει ταχύτητα 2 m/s και κινείται μέσα στο ομογενές μαγνητικό πεδίο οπότε στα άκρα της αναπτύσσεται επαγωγική τάση Εεπαγ = Β υ l , συνεπώς διαρρέεται με ρεύμα i = Εεπαγ / Rολ , η συνολική αντίσταση του κυκλώματος είναι : Rολ = RΚΛ + R1 R2 / (R1 + R2) = 2 + 6 3 / (6 + 3) => Rολ = 4 Ω
έτσι η ράβδος δέχεται δύναμη Laplace : FL = B i l = B2 l2 v / Rολ αντίρροπη της F
συνεπώς : ΣF = m a => F - FL = m a => F - B2 l2 v / Rολ = m a
επειδή η ράβδος κινείται με σταθερή ταχύτητα α = 0 οπότε
F - B2 l2 v / Rολ = 0 => 0,5 = B2 12 2 / 4 => Β = 1 Τ
Γ4.
από 0 έως 2s η ράβδος μετακινείται κατά x1 = ½ α t2 = ½ 1 22 = 2 m
από 2s έως 5s η ράβδος μετακινείται κατά x2 = v t = 2 3 = 6 m
έργο που παράγει η F WF = F x = 0,5 ( 2 m + 6 m ) = 4 J
Εεπαγ = Β υ l = 1 2 1 = 2 Volt i = Εεπαγ / Rολ = 2 V / 4 Ω = 0,5 A
VΚΛ = Εεπαγ - i RΚΛ = 2 - 0,5 2 = 1 Volt i2 = VΚΛ / R2 = 1 V / 3 Ω = 1/3 A
QR2 = i22 R2 t = (1/3)2 3 (5 - 2) = 1 J
QR2 / WF = 1J / 4J = 0,25 ή 25 %
ΘΕΜΑ 32. θέμα Γ 
Οι ευθύγραμμοι αγωγοί μεγάλου μήκους Αx και Γy είναι κατακόρυφοι, έχουν αμελητέα ηλεκτρική αντίσταση, είναι στερεωμένοι σε οριζόντιο μονωτικό επίπεδο και απέχουν απόσταση L=1m μεταξύ τους. Στα άκρα τους, Α και Γ, είναι συνδεδεμένος αντιστάτης με αντίσταση R1=3Ω. Η διάταξη βρίσκεται σε
χώρο που υπάρχει οριζόντιο ομογενές μαγνητικό πεδίο έντασης Β=2Τ, με φορά από τον αναγνώστη προς τη σελίδα. Λεπτή αγώγιμη οριζόντια ράβδος ΚΛ με μάζα m=0,5kg και αντίσταση R2=1Ω, έχει τα άκρα της Κ και Λ εφαπτόμενα στους αγωγούς Αχ και Γψ. Τη χρονική στιγμή t0=0s εκτοξεύουμε τη ράβδο με αρχική ταχύτητα υ0=4m/s προς τα κάτω και τη χρονική στιγμή t1, που η επιτάχυνση της ράβδου μηδενίζεται, η ταχύτητά της είναι ίση με υ1=1m/s.
Γ1. i. Να βρείτε και να δικαιολογήσετε τη φορά του ρεύματος που διαρρέει το κλειστό κύκλωμα ΑΓΛΚΑ.
ii. Να βρείτε τη φορά και το μέτρο της δύναμης Laplace που θα ασκηθεί στη ράβδο ΚΛ αμέσως μετά την εκτόξευση.
iii. Να ελέγξετε αν οι κατακόρυφοι οδηγοί ασκούν δυνάμεις τριβής στη ράβδο και στην περίπτωση που ασκούν, να βρείτε το μέτρο της συνισταμένης τους.
Γ2. Να υπολογίσετε την ταχύτητα της ράβδου τη χρονική στιγμή που το μέτρο της επιτάχυνσης της ράβδου είναι 2m/s2
Γ3. Να υπολογίσετε τη μετατόπιση της ράβδου από τη χρονική στιγμή t0 μέχρι τη χρονική στιγμή που η ταχύτητα υποδιπλασιάζεται, αν ως τότε απελευθερώθηκε στις αντιστάσεις θερμική ενέργεια Q=4,5J.
Γ4. Να σχεδιάσετε σε αριθμημένους άξονες το διάγραμμα του λόγου PRολ /|PΤ| σε συνάρτηση με την ταχύτητα της ράβδου, όπου PRολ η ισχύς στις αντιστάσεις και PT ο ρυθμός μετατροπής ενέργειας σε θερμική λόγω των τριβών. Δίνεται g=10m/s2.
Γ1. Η ράβδος ΚΛ καθώς κινείται προς τα κάτω μέσα στο μαγνητικό πεδίο, τα ηλεκτρόνιά της δέχονται δύναμη Lorentz και οδεύουν προς το άκρο Κ το οποίο φορτίζεται αρνητικά με την πάροδο του χρόνου, ενώ το άκρο Λ φορτίζεται θετικά. Στα άκρα Κ, Λ ανατύσσεται τάση από επαγωγή : Εεπαγ = B L v. Το κλειστό κύκλωμα ΚΑΓΛΚ διαρρέεται με ρεύμα εντάσεως i = Εεπαγ / (R1 + R2) = B L v / (R1 + R2) με συνέπεια η ράβδος ΚΛ καθώς κινείται προς τα κάτω μέσα στο μαγνητικό πεδίο να δέχεται δύναμη Laplace αντίρροπη του βάρους της FL = B L i = B2 L2 v / (R1 + R2) Αρχικά η ταχύτητα της ράβδου είναι υ0 οπότε το μέτρο της δύναμης Laplace είναι : FL = B2 L2 v0 / (R1 + R2) = = 22 12 4 / (3 + 1 ) = 4 Ν με κατεύθυνση κατακόρυφη προς τα πάνω
Έστω υπάρχουν τριβές Τ τότε : ΣF = m a => m g - T - FL = m a => m g - T - B2L2v / (R1 + R2) = m a => 0,5 10 - T - 2212v / 4 = 0,5 a => 5 - T - v = 0,5 a (1)
τελικά υ = 1 m/s και α = 0 τότε η (1) => 5 - T - 1 = 0 => Τ = 4 Ν
αρχικά υ = 4 m/s η (1) => 5 - 4 - 4 = 0,5 a => - 3 = 0,5 α => α = - 6 m/s2 επιβράδυνση
η ράβδος διαρρέεται από ρεύμα i = Εεπαγ / (R1 + R2) = BLv /(R1+R2) = 2 1 4 / 4 = 2 Α
Γ2. τη στιγμή που α = - 2 m/s2 η (1) => 5 - 4 - υ = 0,5 (- 2) => υ = + 2 m/s κατεύθυνση προς τα κάτω
Γ3. τη στιγμή που v = v0 / 2 = 4 / 2 = 2 m/s η ράβδος διαρρέεται από ρεύμα i = Εεπαγ / (R1 + R2) = BLv /(R1+R2) = 2 1 2 / 4 = 1 Α
έστω η ράβδος μετατοπίζεται κατακόρυφα κατά ψ το έργο της δύναμης Laplace μετατρέπεται σε θερμότητα πάνω στις αντιστάσεις είναι : WFL = Qθερμ = 4,5 J
διατήρηση ενέργειας : ½ m v02 + m g ψ = ½ m v2 + WFL + T ψ =>
=> ½ 0,5 42 + 0,5 10 ψ = ½ 0,5 22 + 4,5 + 4 ψ => 4 + 5 ψ = 1 + 4,5 + 4 ψ => ψ = 1,5 m
Γ4. PRολ = i2 (R1 + R2) = ( BLv /(R1+R2) )2 (R1+R2) = B2 L2 v2 / (R1+R2) = 4 1 υ2 / 4 = υ2
|ΡΤ| = Τ υ = 4 υ τότε ο λόγος : PRολ /|PΤ| = υ2 / 4υ = υ / 4
5 - T - v = 0,5 a => 5 - 4 - v = 0,5 dv/dt => 1 - v = 0,5 dv/dt => dv / (v - 1) = - 2 dt =>
=> ln { (v - 1) / (4 - 1) } = - 2 t => v - 1 = 3 e-2t => v(t) = 1 + 3 e-2t
v(0) = 1 + 3 1 = 4 m/s αρχική ταχύτητα , όταν t ® ¥ v = 1 m/s οριακή ταχύτητα
a = dv / dt => a(t) = - 6 e-2t < 0 επιβραδυνόμενη κίνηση ράβδου a(0) = - 6 m/s2 αρχική επιτάχυνση , όταν t ® ¥ a = 0 τελική επιτάχυνση
v = dx / dt => dx = v dt = ( 1 + 3 e-2t ) dt => x = t + 3/(-2) [ e-2t - 1 ] => x(t) = t + 3/2 - 3/2 e-2t
t = 0 x(0) = 0 όταν t ® ¥ x(t) = t + 3/2
ΘΕΜΑ 33. θέμα Δ
Η οριζόντια μεταλλική ράβδος ΚΛ μήκους L=0,5 m, μάζας m=0,5kg, έχει ωμική αντίσταση R2=0,1Ω και συγκρατείται ακίνητη πάνω στους κατακόρυφους, αγώγιμους – αμελητέας αντίστασης – οδηγούς Αx και Γy. Στο χώρο υπάρχει οριζόντιο ομογενές μαγνητικό πεδίο έντασης Β=2Τ, κάθετο στη ράβδο ΚΛ, όπως φαίνεται στο σχήμα. Τα άκρα Α, Γ συνδέονται με αντίσταση R1=0,4Ω. 
Τη χρονική στιγμή t=0, εκτοξεύουμε τη ράβδο ΚΛ προς τα κάτω με αρχική ταχύτητα υ0=2m/s, η οποία κινείται δεχόμενη από τους δύο οδηγούς συνολική τριβή μέτρου Τ=2Ν. Μετά από μετατόπιση y=2m, ο αγωγός αποκτά σταθερή ταχύτητα.
α) Να προσδιορίσετε τη φορά και την ένταση του επαγωγικού ρεύματος που διαρρέει το κύκλωμα αμέσως μετά την εκτόξευση της ράβδου.
β) Να προσδιορίσετε το είδος της κίνησης που θα εκτελέσει η ράβδος και να βρείτε τη σταθερή (οριακή) ταχύτητα υορ, που θα αποκτήσει ο αγωγός.
γ) Να υπολογίσετε τη θερμική ενέργεια που εκλύθηκε στους ωμικούς αντιστάτες μέχρι τη στιγμή που η ράβδος αποκτάει την οριακή ταχύτητα.
δ) Να υπολογίσετε το ρυθμό μεταβολής της δυναμικής ενέργειας τη χρονική στιγμή t1, που η δύναμη Laplace ισούται με 3,5Ν.
ε) Να υπολογίσετε τη διαφορά δυναμικού στην αντίσταση R2, τη χρονική στιγμή t1.
Δίνεται η επιτάχυνση της βαρύτητας g= 10 m/s2.
Εεπαγ = Β L v i = Εεπαγ / ( R1 + R2 ) = Β L v / ( R1 + R2 ) = 2 0,5 v / 0,5 = 2 v
FL = B L i = 2 0.5 2v = 2 v
ΣF = m a => m g - T - FL = m a => 0,5 10 - 2 - 2 v = 0,5 a => 3 - 2 v = 0,5 dv/dt =>
=> - 2 ( v - 1,5 ) = 0,5 dv/dt => dv/(v - 1,5) = - 4 dt => ln [ ( v - 1,5 ) / ( 2 - 1,5 ) ] = - 4 t =>
=> v - 1,5 = 0,5 e-4t => v(t) = 1,5 + 0,5 e-4t
a(t) = - 2 e-4t η ράβδος εκτελεί επιβραδυνόμενη κίνηση
v = dx/dt => dx = v dt = ( 1,5 + 0,5 e-4t ) dt => x(t) = 1,5 t - 0,125 ( e-4t - 1 )
t = 0 : v(0) = 1,5 + 0,5 = 2 m/s a(0) = - 2 m/s2 x(0) = 0
t ® ¥ : v = 1,5 m/s οριακή ταχύτητα a = 0 x = 1,5 t + 0,125
t = 5/4 s x = 1,5 5/4 + 1/8 = 16/8 = 2 m
i(t) = 2 v(t) = 3 + e-4t (A) FL (t) = B L i(t) = 3 + e-4t (N)
VR2 = i R2 = 0,4 ( 3 + e-4t ) = 1,2 + 0,4 e-4t (V)
PR = i2 ( R1 + R2 ) = 0,5 ( 3 + e-4t )2 PFL = FL v = ( 3 + e-4t ) ( 1,5 + 0,5 e-4t ) = 0,5 ( 3 + e-4t )2 = PR
PT = T v = 2 ( 1,5 + 0,5 e-4t ) => ΡΤ = 3 + e-4t
U = m g h = m g ( H - y )
dU/dt = - m g dy/dt = - m g v(t) = - 0,5 10 ( 1,5 + 0,5 e-4t ) = - 5 ( 1,5 + 0,5 e-4t ) => dU/dt (t) = - 7,5 - 2,5 e-4t
K = 0,5 m v2 dK/dt = m v a = 0,5 ( 1,5 + 0,5 e-4t ) ( - 2 e-4t ) => dK/dt = - e-4t ( 1,5 + 0,5 e-4t )
FL = 3,5 N => 3 + e-4t = 3,5 => e-4t = 0,5
PR = 0,5 ( 3 + e-4t )2 = 0,5 ( 3 + 0,5 )2 = 6,125 Watt = PFL
PT = 3 + e-4t = 3 + 0,5 = 3,5 J/s
dU/dt = - 7,5 - 2,5 e-4t = - 7,5 - 2,5 0,5 = - 8,75 J/s = ( Uτελ - Uαρχ ) / Δt
dK/dt = - e-4t ( 1,5 + 0,5 e-4t ) = - 0,5 ( 1,5 + 0,5 0,5 ) = - 0,875 J/s = ( Κτελ - Καρχ ) / Δt
διατήρηση ενέργειας : Uαρχ + Kαρχ = Uτελ + Kτελ + WT + WFL =>
=> Uαρχ - Uτελ = Kτελ - Kαρχ + WT + WFL =>
=> - dU/dt = dK/dt + PT + PR => 8,75 J/s = - 0,875 J/s + 3,5 J/s + 6,125 Watt
Uαρχ - Uτελ - WT - WFL = Kτελ - Kαρχ => 8,75 J/s - 3,5 J/s - 6,125 Watt = - 0,875 J/s Θ.Μ.Κ.Ε.
- ( - 7,5 - 2,5 e-4t ) = - e-4t ( 1,5 + 0,5 e-4t ) + 3 + e-4t + 0,5 ( 3 + e-4t )2 => - dU/dt = dK/dt + PT + PFL
VR2 = 1,2 + 0,4 e-4t = 1,2 + 0,4 0,5 = 1,4 V
Qθερμ = ¦ PR dt = ¦ 0,5 ( 3 + e-4t )2 dt = ¦ 0,5 ( 9 + 6 e-4t + e-8t ) dt =
= 0,5 ( 9 t - 1,5 ( e-4t - 1 ) - 0,125 ( e-8t - 1 ) ) = 4,5 t - 0,75 ( e-4t - 1 ) - 0,0625 ( e-8t - 1 )
t = 5/4 s : Qθερμ = 4,5 5/4 + 0,75 + 0,0635 = 6,4375 J
ΘΕΜΑ 34. θέμα Δ
Η οριζόντια μεταλλική ράβδος ΚΛ μήκους L=1m, μάζας m=0,5kg, έχει ωμική αντίσταση R1=0,1Ω και συγκρατείται ακίνητη πάνω στους κατακόρυφους, αγώγιμους – αμελητέας αντίστασης – οδηγούς Αx και Γy. Στο χώρο υπάρχει οριζόντιο ομογενές μαγνητικό πεδίο έντασης Β=0,3Τ, κάθετο στη ράβδο ΚΛ, όπως φαίνεται στο σχήμα.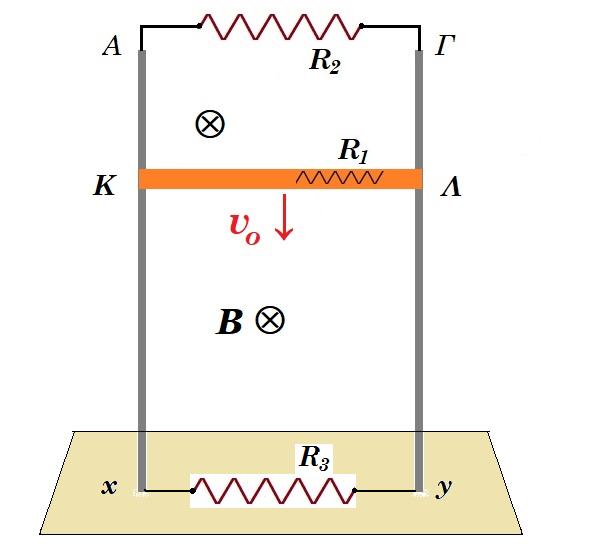 Τα άκρα Α, Γ συνδέονται με αντίσταση R2=0,3Ω ενώ στη βάση του οριζόντιου μονωτικού επιπέδου υπάρχει αντίσταση R3=0,6Ω. Τη χρονική στιγμή t=0, εκτοξεύουμε τη ράβδο ΚΛ προς τα κάτω με αρχική ταχύτητα υ0=2m/s, η οποία κινείται δεχόμενη από τους δύο οδηγούς συνολική τριβή μέτρου Τ=2Ν. Μελετήστε την κίνηση της ράβδου.
Τα άκρα Α, Γ συνδέονται με αντίσταση R2=0,3Ω ενώ στη βάση του οριζόντιου μονωτικού επιπέδου υπάρχει αντίσταση R3=0,6Ω. Τη χρονική στιγμή t=0, εκτοξεύουμε τη ράβδο ΚΛ προς τα κάτω με αρχική ταχύτητα υ0=2m/s, η οποία κινείται δεχόμενη από τους δύο οδηγούς συνολική τριβή μέτρου Τ=2Ν. Μελετήστε την κίνηση της ράβδου.
Πόση απόσταση διανύει η ράβδος κατερχόμενη μέχρι να αποκτήσει σταθερή ταχύτητα ;
Πόση θερμική ενέργεια εκλύθηκε στους ωμικούς αντιστάτες μέχρι τη στιγμή που η ράβδος αποκτάει την οριακή ταχύτητας ;
Εεπαγ = Β L v R2,3 = R2 R3 / (R2 + R3) = 0,2Ω i = Εεπαγ /(R1 + R2,3) = Β L v / (R1 + R2,3) = 0,3 1 v / 0,3 = v
FL = B L i = Β2 L2 v / ( R1 + R2,3 ) = 0,3 1 v = 0,3 v
ΣF = m a => m g - T - FL = m a (1) => m g - T - Β2 L2 v / ( R1 + R2,3 ) = m a =>
=> - Β2L2/(R1 + R2,3) [ v - (mg - T)(R1 + R2,3)/ Β2L2 ] = m dv/dt =>
=> dv / [ v - (mg - T)(R1 + R2,3)/ Β2L2 ] = - Β2L2/ m(R1 + R2,3) dt => Β2L2/ m(R1 + R2,3) = 1/τ
=> ¦ dv / [ v - u* ] = ¦ - 1/τ dt => (mg - T)(R1 + R2,3)/ Β2L2 = u*
=> ln [ ( v - u* ) / ( v0 - u* ) ] = - t/τ =>
=> ( v - u* ) = ( v0 - u* ) e- t/τ => v(t) = u* + ( v0 - u* ) e- t/τ
a = dv / dt => a(t) = - 1/τ ( v0 - u* ) e- t/τ
v = dx/dt => dx = v dt = [ u* + ( v0 - u* ) e- t/τ ] dt => x(t) = u* t - τ ( v0 - u* ) ( e- t/τ - 1 )
(1) => 0,5 10 - 2 - 0,3 v = 0,5 a => 3 - 0,3 v = 0,5 dv/dt =>
=> - 0,3 ( v - 10 ) = 0,5 dv/dt => dv / (v - 10) = - 0,6 dt => ln [ ( v - 10 ) / ( 2 - 10 ) ] = - 0,6 t =>
=> v - 10 = - 8 e-0,6t => v(t) = 10 - 8 e-0,6t
a(t) = + 8 0,6 e-0,6t = + 4,8 e-0,6t η ράβδος εκτελεί επιταχυνόμενη κίνηση
v = dx/dt => dx = v dt = ( 10 - 8 e-0,6t ) dt => x(t) = 10 t + 40/3 ( e-0,6t - 1 )
t = 0 : v(0) = 10 - 8 = +2 m/s a(0) = +4,8 m/s2 x(0) = 0
t ® ¥ : v = 10 m/s οριακή ταχύτητα a = 0 x = 10 t - 40/3
t = 5/0,6 s τότε x = 10 5/0,6 - 40/3 = 250/3 - 40/3 = 70 m
i(t) = v(t) = 10 - 8 e-0,6t (A) FL (t) = B L i(t) = 3 - 2,4 e-0,6t (N)
Vπολική = VΛΚ = Εεπαγ - i R1 = B L v(t) - i R1 = 0,3 1 ( 10 - 8 e-0,6t ) - ( 10 - 8 e-0,6t ) 0,1 = 2 - 1,6 e-0,6t
VR2 = i2 R2 => 2 - 1,6 e-0,6t = i2 0,3 => i2(t) = 20/3 - 16/3 e-0,6t (V)
PR = i2 ( R1 + R2,3 ) = 0,3 ( 10 - 8 e-0,6t )2
PFL = FL v = ( 3 - 2,4 e-0,6t ) ( 10 - 8 e-0,6t ) = 0,3 ( 10 - 8 e-0,6t )2 = PR
PT = T v = 2 ( 10 - 8 e-0,6t ) = 20 - 16 e-0,6t
U = m g h = m g ( H - y )
dU/dt = - m g dy/dt = - m g v(t) = - 0,5 10 ( 10 - 8 e-0,6t ) = - 50 + 40 e-0,6t
K = 0,5 m v2 dK/dt = m v a = 0,5 ( 10 - 8 e-0,6t ) 4,8 e-0,6t = 2,4 e-0,6t ( 10 - 8 e-0,6t )
διατήρηση ενέργειας : Uαρχ + Kαρχ = Uτελ + Kτελ + WT + WFL => Uαρχ - Uτελ = Kτελ - Kαρχ + WT + WFL =>
=> - dU/dt = dK/dt + PT + PR =>
=> 50 - 40 e-0,6t = 2,4 e-0,6t ( 10 - 8 e-0,6t ) + 20 - 16 e-0,6t + 0,3 ( 10 - 8 e-0,6t )2 =>
=> 50 - 40 e-0,6t = 24 e-0,6t - 19,2 e-1,2t + 20 - 16 e-0,6t + 30 - 48 e-0,6t + 19,2 e-1,2t
για να βρούμε την θερμότητα που αναπτύσσεται πάνω στις αντιστάσεις θα ολοκληρώσουμε την ισχύ από t = 0 έως t
Qθερμ = ¦ PR dt = ¦ 0,3 ( 10 - 8 e-0,6t )2 dt = ¦ 0,3 ( 100 - 160 e-0,6t + 64 e-1,2t ) dt =
= 0,3 [ 100 t + 160/0,6 ( e-0,6t - 1 ) - 64/1,2 ( e-1,2t - 1 ) ] = 30 t + 80 ( e-0,6t - 1 ) - 16 ( e-1,2t - 1 )
t = 5/0,6 s : Qθερμ = 30 5/0,6 - 80 + 16 = 186 J = WFL θερμότητα που εκλύεται πάνω στις αντιστάσεις ισούται με το έργο της δύναμης Laplace
η ράβδος αρχικά είχε ταχύτητa v0 = 2 m/s και κινητική ενέργεια K = 0,5 m v02 = 0,5 0,5 22 = 1 J
μετά από χρόνο t = 5/0,6 s έχει αποκτήσει οριακή ταχύτητα vορ = 10 m/s και κινητική ενέργεια K = 0,5 m vορ2 = 0,5 0,5 102 = 25 J και έχει μετατοπισθεί κατακόρυφα προς τα κάτω κατά h = 70 m η αρχική δυναμική ενέργειά της είναι U = m g h = 0,5 10 70 = 350 J και το έργο των τριβών είναι WT = T h = 2 N 70 m = 140 J
έχουμε διατήρηση ενέργειας : 350 J + 1 J = 25 J + 140 J + 186 J
Uαρχ + Kαρχ = Kτελ + WT + WFL