
( εφθ )' = ( συνθ / ημθ )' = [ ( συνθ )' . ημθ - συνθ . ( ημθ )' ] / ημ2θ =
= ( - ημθ . ημθ - συνθ . συνθ ) / ημ2θ = - 1 / ημ2θ
Biot - Savart
ημθ = α / r => r = α / ημθ x < 0
εφθ = α / (-x) => x = - α / εφθ => dx = - α . ( - 1 / ημ2θ ) . dθ = ( α / ημ2θ ) . dθ
dB = μο Ι . dx . ημθ = μο Ι . ( α / ημ2θ ) . dθ . ημθ = μο . Ι . ημθ . dθ
4π r2 4π ( α / ημθ )2 4π . α
B = ΣdB = μο . Ι . θ1Σθ2 ημθ . dθ = μο . Ι . [- συνθ ]θ1 θ2 = 4π . α 4π . α
= μο . Ι . ( συνθ1 - συνθ2 )
4π . α

~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
 ΘΕΜΑ 4
ΘΕΜΑ 4
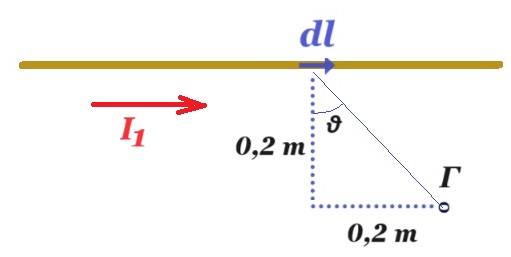
Ευθύγραμμος ρευματοφόρος αγωγός (1) μεγάλου μήκους διαρρέεται από συνεχές ρεύμα σταθερής έντασης 𝛪1 = 2 𝛢.
4.1. Να υπολογίσετε το μέτρο και προσδιορίστε την κατεύθυνση της έντασης 𝛥𝐵⃗ του μαγνητικού πεδίου που δημιουργείται στο σημείο Γ του σχήματος εξαιτίας του στοιχειώδους τμήματος 𝛥𝑙 = 0,02 𝑚.
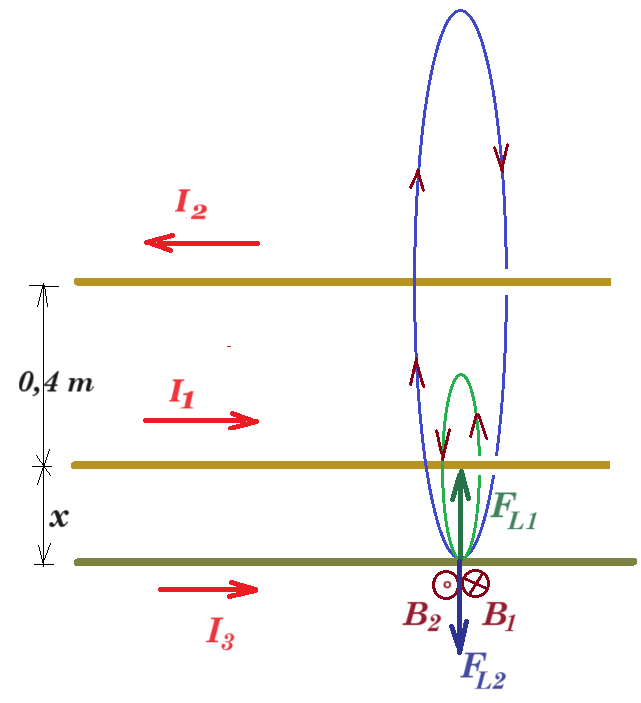
Παράλληλα προς τον αγωγό (1) και σε απόσταση 0,4 𝑚 από αυτόν, τοποθετούμε άλλον ευθύγραμμο ρευματοφόρο αγωγό (2) μεγάλου μήκους, ο οποίος διαρρέεται από αντίρροπο συνεχές ρεύμα σταθερής έντασης 𝛪2 = 4 𝛢.
4.2. Να υπολογίσετε την ένταση του μαγνητικού πεδίου στο μέσο Μ της απόστασης ανάμεσα στους δύο αγωγούς.
4.3. Να βρείτε που πρέπει να τοποθετηθεί τρίτος ρευματοφόρος αγωγός παράλληλα στους (1) και (2) ώστε να μην δέχεται μαγνητική δύναμη Laplace από αυτούς.
dB = 10-7 N/A2 I1 dl ημθ / r2 = 10-7 N/A2 2 A √2/2 0,02 m / 0,08 m2 = √2/4 10-7 T
Β(Μ) = Β1 + Β2 = 10-7 Ν/Α2 2 2 Α / 0,2 m + 10-7 Ν/Α2 2 4 Α / 0,2 m = 6.10-6 T 
B1 = B2 => 10-7 2 2 / x = 10-7 2 4 / (0,4 + x) => 2x = 0,4 + x => x = 0,4 m
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
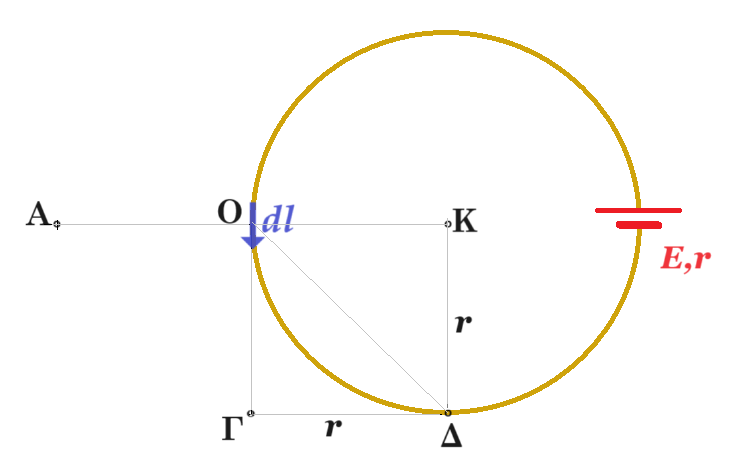
Στο επίπεδο της σελίδας υπάρχει ένας κυκλικός αγωγός κέντρου Κ και ακτίνας r, ο οποίος διαρρέεται από ρεύμα σταθερής έντασης Ι, όπως στο σχήμα. Ένα στοιχειώδες τμήμα dl του αγωγού με μέσον το σημείο Ο το κύκλου, δημιουργεί στο κέντρο Κ του αγωγού μαγνητικό πεδίο έντασης dΒ1. Στο σχήμα βλέπετε τρία σημεία Α, Γ και Δ, όπου το Α είναι συμμετρικό του Κ ως προς το Ο, το Δ είναι στο άκρο μιας ακτίνας κάθετης στην ακτίνα ΟΚ, ενώ το σημείο Γ απέχει κατά r από το Δ, όπου η ΓΔ είναι κάθετη στην ΚΔ.
α) Να σχεδιάσετε την ένταση του μαγνητικού πεδίου στα τρία σημεία Α, Γ και Δ, που οφείλεται στο τμήμα dl του αγωγού.
β) Να υπολογίσετε τα μέτρα των τριών παραπάνω εντάσεων συναρτήσει της έντασης dΒ1 της έντασης στο κέντρο Κ του αγωγού.
στο σημείο Κ : dB1 = 10-7 ( I dl / r2 ) ημθ = 10-7 ( I dl / (ΟΚ)2 ) ημ90° = 10-7 I dl / r2 με διεύθυνση κάθετη στο επίπεδο του κύκλου και φορά προς τα έξω
στο σημείο Α : dB2 = 10-7 ( I dl / r2 ) ημθ = 10-7 ( I dl / (ΟΚ)2 ) ημ90° = 10-7 I dl / r2 = dB1 με διεύθυνση κάθετη στο επίπεδο του κύκλου και φορά προς τα μέσα
στο σημείο Δ : dB3 = 10-7 ( I dl / r2 ) ημθ = 10-7 ( I dl / (ΟΔ)2 ) ημ45° = 10-7 ( I dl / 2r2 ) √2/2 = dB1 √2/4 με διεύθυνση κάθετη στο επίπεδο του κύκλου και φορά προς τα έξω
στο σημείο Γ : dB4 = 10-7 ( I dl / r2 ) ημθ = 10-7 ( I dl / r2 ) ημ0° = 0