Μάθημα : Μαθηματικά A' Γυμνασίου
Κωδικός : 0501628300
G56133-01 - Μανιατοπούλου Αμαλία
Η πλατφόρμα σάς ανακατεύθυνε αυτόματα στην αρχική σελίδα για να συνδεθείτε προτού προχωρήσετε σε άλλες ενέργειες. Πιθανόν, να έληξε η σύνοδός σας.
Περιγραφή Μαθήματος

Θεωρία και ασκήσεις. Μικροεφαρμογές που μπορούμε να δοκιμάσουμε στον υπολογιστή μας και να κάνουμε εικονικά πειράματα ώστε να "δούμε" αυτά που έχουμε πει στην τάξη. Αλλά και κάποιες δοκιμασίες (τεστ) για να ξέρουμε τι καταλάβαμε. Για απορίες μπορείτε να στείλετε μήνυμα μέσα από την η-τάξη ή στο amaniato@sch.gr
Το υλικό είναι κυρίως από το εμπλουτισμένο βιβλίο μαθητή.
από 1/10/20 έως 30/6/21
Υλικό από τις παραγράφους 1.1 με 1.4 του Β' μέρους του βιβλίου. Είμαστε στη Γεωμετρία κι έτσι έχουμε αρκετές μικροεφαμογές για να δούμε τις έννοιες αυτές.
Έννοιες όπως σημείο. ευθεία, επίπεδο που πρέπει να τις νοιώσουμε κι όχι να τις ορίσουμε. Δεν ξεχνάμε ότι
- Η ευθεία δεν έχει ούτε αρχή ούτε τέλος
- Aπό ένα σημείο διέρχονται άπειρες ευθείες.
- Aπό δύο σημεία διέρχεται μια μόνο ευθεία.
Αντίσοτιχα για το επίπεδο:
- Ένα επίπεδο επεκτείνεται απεριόριστα.
- Από τρία μη συνευθειακά σημεία διέρχεται ένα μοναδικό επίπεδο, ενώ από ένα ή δύο σημεία διέρχονται άπειρα επίπεδα.
- Κάθε επίπεδο χωρίζει τον χώρο σε δύο μέρη, ώστε, αν θέλουμε να περάσουμε από το ένα μέρος του χώρου στο άλλο, πρέπει να διαπεράσουμε το επίπεδο.
- Η ονομασία του επιπέδου δίνεται με ένα κεφαλαίο γράμμα του αλφάβητου π.χ. Π, Ρ, Σ κ.λπ.
- Κάθε ευθεία ενός επιπέδου το χωρίζει σε δύο ημιεπίπεδα
Όμως μπορούμε να ορίσουμε την ημιευθεία και το ευθύγραμμο τμήμα:
Η ημιευθεία είναι ένα κομμάτι της ευθείας από ένα σημείο (που το λέμε αρχή) και μετά. Εάν Ο είναι ένα σημείο της ευθείας x'x, τότε με αρχή το Ο ορίζονται δύο ημιευθείες οι Οx' και Οx, οι οποίες λέγονται αντικείμενες ημιευθείες.
Ευθύγραμμο τμήμα είναι ένα κομμάτι της ευθείας ανάμεσα σε δυο σημεία που τα λέμε άκρα του ευθυγράμμου τμήματος. Δυο ευθύγραμμα τμήματα λέγονται διαδοχικά όταν το ένα αρχίζει εκεί που τελειώνει το άλλο (δεν έχουν άλλα κοινά σημεία). Αν πάρουμε πολλά (από τρία και πάνω) διαδοχικά ευθύγραμμα τμήματα έτσι ώστε να μην ανήκουν στην ίδια ευθεία και το τέλος του τελευταίου να συμπίπτει με την αρχή του πρώτου τότε φτιάχνουμε ένα πολύγωνο και τα ευθύγραμμα τμήματα αυτά τα λέμε πλευρές ενώ τα άκρα τους κορυφές του πολυγώνου. Τα ευθύγραμμα τμήματα που ενώνουν δυο μη διαδοχικές κορυφές τα λέμε διαγωνίους του πολυγώνου. Τα πολύγωνα τα ονομάζουμε με τον αριθμό των κορυφών και την κατάληξη -γωνο εκτός απ' την περίπτωση που έχουμε 4 κορυφές οπότε μιλάμε για τετράπλευρο (αν π.χ. ένα πολύγωνο έχει ν πλευρές το λέμε νίγωνο).
Τεθλασμένη γραμμή είναι το σχήμα που αποτελείται από διαδοχικά ευθύγραμμα τμήματα, τα οποία δεν βρίσκονται όλα στην ίδια ευθεία. Μια τεθλασμένη γραμμή ονομάζεται κυρτή, όταν η προέκταση κάθε πλευράς της αφήνει όλες τις άλλες πλευρές στο ίδιο ημιεπίπεδο. Διαφορετικά λέγεται μη κυρτή.
Δύο ευθύγραμμα σχήματα λέγονται ίσα, αν συμπίπτουν, όταν τοποθετηθούν το ένα επάνω στο άλλο με κατάλληλο τρόπο. Στα ίσα σχήματα, τα στοιχεία που συμπίπτουν, δηλαδή οι κορυφές, οι πλευρές και οι γωνίες, ονομάζονται αντίστοιχα στοιχεία των σχημάτων αυτών. Οι αντίστοιχες πλευρές και γωνίες των ίσων σχημάτων είναι ίσες.
Για να συγκρίνουμε μεταξύ τους ευθύγραμμα τμήματα χρησιμοποιούμε μια κοινή μονάδα σύγκρισης. Έτσι, κάθε σύγκριση ενός μεγέθους με την αντίστοιχη μονάδα λέγεται μέτρηση. Για το μήκος έχουμε μονάδα μήκους το μέτρο (m). Εάν όμως το μήκος του ευθύγραμμου τμήματος είναι πολύ μεγαλύτερο ή πολύ μικρότερο από το μήκος του μέτρου, επιλέγουμε, για τη μέτρηση ένα πολλαπλάσιο ή μια υποδιαίρεση του μέτρου για τον σκοπό αυτό.
Aπόσταση δύο σημείων Α και Β λέγεται το μήκος του ευθύγραμμου τμήματος ΑΒ, που τα ενώνει. Με το σύμβολο ΑΒ εννοούμε ταυτόχρονα δύο διαφορετικά πράγματα: Το ευθύγραμμο τμήμα ΑΒ, αλλά και το μήκος αυτού του ευθύγραμμου τμήματος ΑΒ.
Μέσο ενός ευθύγραμμου τμήματος ΑΒ ονομάζουμε το σημείο Μ του τμήματος, που απέχει εξίσου από τα άκρα του. Οποιοδήποτε ευθύγραμμο τμήμα ΑΒ έχει πάντα ένα μέσο Μ, που είναι και μοναδικό.
Μπορώ να προσθέσω ευθύγραμμα τμήματα αν τα κάνω διαδοχικά. Μπορώ να αφαιρέσω δυο ευθύγραμμα τμήματα αν τα βάλω να έχουν κοινή αρχή.
Μια τεθλασμένη γραμμή έχει μήκος το άθροισμα των μηκών των ευθυγράμμων τμημάτων, από τα οποία αποτελείται.
Το μήκος του ευθύγραμμου τμήματος ΑΒ, είναι μικρότερο από το μήκος κάθε τεθλασμένης γραμμής με τα ίδια άκρα Α και Β.
Το άθροισμα των πλευρών ενός ευθύγραμμου σχήματος, το λέμε περίμετρο του σχήματος.
Κάντε τις παρακάτω ασκήσεις και μετά την εργασία που πρέπει να υποβάλετε έγκαιρα!
από 15/9/20 έως 30/6/21
Ας θυμηθούμε (βιβλίο σελίδες 34 - 43):
Στα Μαθηματικά το "κλάσμα" δηλώνει σε πόσα ίσα μέρη χωρίσαμε το ολόκληρο (τον "όλον") και πόσα από αυτά πήραμε.
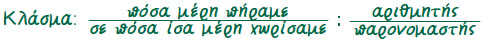 (παρονομαστής όχι μηδέν).
(παρονομαστής όχι μηδέν).
Δοκιμάστε να γράψετε μερικά κλάσματα. Κι κάποιος θέλει τα πιο δύσκολα, δεν έχει παρά να δοκιμάσει.
Αν ο αριθμητής είναι ίσος με 1 έχουμε κλασματική μονάδα. Αν πάρουμε k κλσαματικές μονάδες (κομμάτια) από κάτι που έχουμε χωρίσει σε n ίσα μέρη έχουμε το κλάσμα . Αν πάρουμε πολλές τέτοιες μονάδες παραπάνω από τα κομμάτια που το κόψαμε (k>n) το κλάσμα λέγεται καταχρηστικό και δείχνει μια διαίρεση του αριθμού k με το n (k : n) και το κλάσμα είναι μεγαλύτερο από το 1.
Κάθε φυσικός αριθμός μπορεί να γραφτεί με την μορφή κλάσματος με παρονομαστή το 1.
Δύο κλάσματα 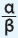 και
και 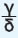 λέγονται ισοδύναμα ή ίσα όταν εκφράζουν το ίδιο τμήμα ενός μεγέθους ή ίσων μεγεθών. Επειδή ακριβώς εκφράζουν το ίδιο τμήμα ενός μεγέθους είναι και ίσα και γράφουμε:
λέγονται ισοδύναμα ή ίσα όταν εκφράζουν το ίδιο τμήμα ενός μεγέθους ή ίσων μεγεθών. Επειδή ακριβώς εκφράζουν το ίδιο τμήμα ενός μεγέθους είναι και ίσα και γράφουμε: 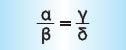
Αν δύο κλάσματα 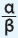 και
και 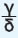 είναι ισοδύναμα τότε τα "χιαστί γινόμενα" α · δ και β · γ είναι ίσα. Δηλαδή:
είναι ισοδύναμα τότε τα "χιαστί γινόμενα" α · δ και β · γ είναι ίσα. Δηλαδή: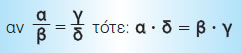
Ισχύει ότι
- Όταν πολλαπλασιαστούν οι όροι ενός κλάσματος με τον ίδιο φυσικό αριθμό (όχι 0) προκύπτει κλάσμα ισοδύναμο.
- Όταν οι όροι ενός κλάσματος διαιρεθούν με τον ίδιο φυσικό αριθμό (όχι 0) προκύπτει κλάσμα ισοδύναμο. (Η διαδικασία αυτή λέγεται απλοποίηση του κλάσματος και έχει ως αποτέλεσμα ένα κλάσμα ισοδύναμο με το αρχικό με μικρότερους όρους).
Το κλάσμα εκείνο που δεν μπορεί να απλοποιηθεί (δεν υπάρχει άλλος κοινός διαιρέτης αριθμητή και παρονομαστή εκτός από τη μονάδα) λέγεται ανάγωγο.
Όταν δύο ή περισσότερα κλάσματα έχουν τον ίδιο παρονομαστή λέγονται ομώνυμα και όταν έχουν διαφορετικούς παρονομαστές ονομάζονται ετερώνυμα.
- Από δύο ομώνυμα κλάσματα, εκείνο που έχει τον μεγαλύτερο αριθμητή είναι μεγαλύτερο.
- Από δύο κλάσματα με τον ίδιο αριθμητή μεγαλύτερο είναι εκείνο με τον μικρότερο παρονομαστή.
- Για να συγκρίνουμε ετερώνυμα κλάσματα τα μετατρέπουμε σε ομώνυμα και συγκρίνουμε τους αριθμητές τους.
Δοκιμάστε πώς τα πάτε. Μέρη του τετραγώνου. Σύγκριση κλασμάτων (2η δραστηριότητα).
Κάντε την παρακάτω άσκηση και μετά την εργασία που πρέπει να υποβάλετε έγκαιρα!
Πατήστε πάνω στους συνδέσμους και δείτε τις μικροεφαρμογές. Χρειάζεται να είναι ενεργοποιημένος ο Adobe Flash Player στον φυλλομετρητή (browser) σας.
Ημερολόγιο
Ανακοινώσεις
Όλες...- - Δεν υπάρχουν ανακοινώσεις -