Μάθημα : Α' ΛΥΚΕΙΟΥ - ΑΛΓΕΒΡΑ

Κωδικός : 0554010269

Α' ΛΥΚΕΙΟΥ - ΑΛΓΕΒΡΑ

0554010269  -  ΣΩΤΗΡΙΑ ΓΟΥΡΝΑ

Περιγραφή Μαθήματος

Μάθημα

Το βιβλίο που κρατάτε στα χέρια σας περιλαμβάνει την ύλη της Άλγεβρας και των Πιθανοτήτων που προβλέπεται από το πρόγραμμα σπουδών της Α’ τάξης του Γενικού Λυκείου.

Το βιβλίο αυτό προήλθε από αναμόρφωση της Α’ έκδοσης (2010) του βιβλίου ΑΛΓΕΒΡΑ Α’ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ, του οποίου τη συγγραφική ομάδα αποτελούν οι Σ. Ανδρεαδάκης, Β. Κατσαργύρης, Σ. Παπασταυρίδης, Γ. Πολύζος και Α. Σβέρκος. Προ­στέθηκαν επίσης δυο ακόμα κεφάλαια: το κεφάλαιο «Πιθανότητες» και το κεφάλαιο «Πρόοδοι».

Το κεφάλαιο «Πιθανότητες» είναι μέρος του αντίστοιχου κεφαλαίου από το βιβλίο ΜΑΘΗΜΑΤΙΚΑ ΚΑΙ ΣΤΟΙΧΕΙΑ ΣΤΑΤΙΣΤΙΚΗΣ Γ’ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ (2010) του οποίου τη συγγραφική ομάδα αποτελούν οι Λ. Αδαμόπουλος, Χ. Δαμιανού και Α. Σβέρκος. Το κεφάλαιο «Πρόοδοι» είναι μέρος του αντίστοιχου κεφαλαίου από το βιβλίο ΑΛΓΕΒΡΑ Β’ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ (2010), του οποίου τη συγγραφική ομάδα αποτελούν οι Σ. Ανδρεαδάκης, Β. Κατσαργύρης, Σ. Παπασταυρίδης, Γ. Πολύζος και Α. Σβέρκος.

  • Περιεχόμενο μαθήματος

    Στο 1° Κεφάλαιο γίνεται μια εισαγωγή στη Θεωρία των Πιθανοτήτων. Η απόδειξη των ιδιοτήτων της πιθανότητας ενός ενδεχομένου γίνεται μόνο στην περίπτωση που τα απλά ενδεχόμενα είναι ισοπίθανα. Η Θεωρία των Πιθανοτήτων ασχολείται με καταστάσεις όπου υπάρχει αβεβαιότητα, και αυτό την κάνει ιδιαίτερα σημαντική στις εφαρμογές της καθημερινής ζωής.

    Στο 2° Κεφάλαιο επαναλαμβάνονται, συμπληρώνονται και επεκτείνονται οι βασικές ιδιότητες των πραγματικών αριθμών.

    Στο 3° Κεφάλαιο επαναλαμβάνονται, επεκτείνονται και εξετάζονται συστηματικά όσα είναι γνωστά από το Γυμνάσιο για τις εξισώσεις 1ου και 2ου βαθμού. Επίσης εξετάζονται εξισώσεις που, για να επιλυθούν, ανάγονται σε 1ου και 2ου βαθμού.

    Στο 4° Κεφάλαιο παρουσιάζονται ανισώσεις 1ου και 2ου βαθμού καθώς και ανισώσεις που, για να επιλυθούν, ανάγονται σε 1ου και 2ου βαθμού.

    Στο 5° Κεφάλαιο γίνεται εισαγωγή στην έννοια της ακολουθίας πραγματικών αριθμών, και εξετάζονται η αριθμητική και η γεωμετρική πρόοδος ως ειδικές περιπτώσεις κανονικότητας (pattern) σε ακολουθίες.

    Στο 6° Κεφάλαιο εισάγεται η έννοια της συνάρτησης. Η συνάρτηση είναι μια θεμελιώδης έννοια που διαπερνά όλους τους κλάδους των Μαθηματικών και έχει κεντρική σημασία για την περαιτέρω ανάπτυξη και εφαρμογή τους.

    Στο 7° Κεφάλαιο γίνεται μελέτη των συναρτήσεων 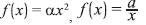piceisa ƒ(x)=αx2, ƒ(x)=α/x και ƒ(x)=αx2+βx+γ. Η μελέτη της ƒ(x)=αx2+βx+γ είναι ο κεντρικός στόχος του κεφαλαίου αυτού.

Ενότητες

ΥΛΗ ΜΑΘΗΜΑΤΟΣ 2024-2025

Εισαγωγικό κεφάλαιο

E.2. Σύνολα

Κεφ.2ο: Οι Πραγματικοί Αριθμοί

2.1 Οι Πράξεις και οι Ιδιότητές τους

2.2 Διάταξη Πραγματικών Αριθμών (εκτός της απόδειξης της ιδιότητας 4)

2.3 Απόλυτη Τιμή Πραγματικού Αριθμού

2.4 Ρίζες Πραγματικών Αριθμών (εκτός των ιδιοτήτων 3 και 4)

Κεφ.3ο: Εξισώσεις

3.1 Εξισώσεις 1ου Βαθμού

3.2 Η Εξίσωση  xν  = α

3.3 Εξισώσεις 2ου Βαθμού

Κεφ.4ο: Ανισώσεις

4.1 Ανισώσεις 1ου Βαθμού

4.2 Ανισώσεις 2ου Βαθμού

Κεφ.5ο: Πρόοδοι

5.1 Ακολουθίες

5.2 Αριθμητική πρόοδος (εκτός της απόδειξης για το “άθροισμα ν διαδοχικών όρων αριθμητικής προόδου”)

5.3 Γεωμετρική πρόοδος (εκτός της απόδειξης για το “άθροισμα ν διαδοχικών όρων γεωμετρικής προόδου”)

Κεφ.6ο: Βασικές Έννοιες των Συναρτήσεων

6.1 Η Έννοια της Συνάρτησης

6.2 Γραφική Παράσταση Συνάρτησης

6.3 Η Συνάρτηση f(x)= αx+β

ΕΙΣΑΓΩΓΙΚΟ ΚΕΦΑΛΑΙΟ Ε.2 ΣΥΝΟΛΑ

Πολλοί άνθρωποι συνηθίζουν να συλλέγουν διάφορα πράγματα, όπως π.χ. γραμματόσημα, νομίσματα, πίνακες ζωγραφικής, εφημερίδες, βιβλία κτλ. Οι περισσότεροι συλλέκτες ταξινομούν τις συλλογές τους σε κατηγορίες, π.χ. «γραμματόσημα που προέρχονται από την ίδια χώρα», «νομίσματα του περασμένου αιώνα», «πίνακες της αναγέννησης» κτλ.
Επίσης από αρχαιοτάτων χρόνων οι άνθρωποι ενδιαφέρθηκαν για τους αριθμούς και τους ταξινόμησαν σε κατηγορίες, όπως είναι π. χ. «οι άρτιοι αριθμοί», «οι πρώτοι αριθμοί» κτλ.

ΚΕΦΑΛΑΙΟ 3ο: Εξισώσεις

1. Αρχαία Αίγυπτος και Βαβυλώνα

  • Αρχαίοι Αιγύπτιοι (1800 π.Χ.): Οι εξισώσεις α' βαθμού εμφανίζονται στον πάπυρο του Ριντ (Rhind Mathematical Papyrus), ένα αρχαίο αιγυπτιακό έγγραφο που περιέχει προβλήματα μαθηματικών. Οι Αιγύπτιοι χρησιμοποιούσαν μεθόδους για να επιλύουν εξισώσεις της μορφής ax=bax = b.Τις έλυναν με διαδικασίες δοκιμής και σφάλματος (μέθοδος "υποθέσεων").

  • Βαβυλώνιοι (2000-1600 π.Χ.): Οι Βαβυλώνιοι κατέγραφαν προβλήματα με εξισώσεις σε πήλινες πινακίδες. Χρησιμοποιούσαν αριθμητικές μεθόδους για την επίλυσή τους, που περιλάμβαναν εξισώσεις της μορφής ax+b=cax + b = c.

2. Αρχαία Ελλάδα

  • Οι αρχαίοι Έλληνες μαθηματικοί, όπως ο Διόφαντος (3ος αιώνας μ.Χ.), ασχολήθηκαν εκτενώς με εξισώσεις, αν και επικεντρώθηκαν περισσότερο στις ρητές λύσεις και όχι στις γραμμικές εξισώσεις ειδικά. Ο Διόφαντος έθεσε τα θεμέλια της αλγεβρικής σκέψης.

3. Ινδία και Ισλαμικός Κόσμος

  • Ινδοί μαθηματικοί (7ος-12ος αιώνας): Ο μαθηματικός Μπαχασκάρα ΙΙ χρησιμοποίησε αλγεβρικές τεχνικές για την επίλυση γραμμικών εξισώσεων. Εισήγαγαν συμβολικές μεθόδους, κάτι που διευκόλυνε την κατανόηση της έννοιας.

  • Ισλαμικοί μαθηματικοί (8ος-14ος αιώνας): Ο Αλ-Χουαρίζμι, στον οποίο οφείλεται η λέξη "αλγεβρα", ασχολήθηκε με την επίλυση εξισώσεων α' βαθμού και παρουσίασε συστηματικές μεθόδους για την επίλυσή τους στο έργο του.

4. Αναγέννηση και Νεότερη Εποχή

  • Στην Ευρώπη της Αναγέννησης, οι γραμμικές εξισώσεις και η αλγεβρική τους επίλυση εξελίχθηκαν σημαντικά. Ο συμβολισμός που χρησιμοποιούμε σήμερα αναπτύχθηκε από μαθηματικούς όπως ο Ρενέ Ντεκάρτ και ο Φρανσουά Βιέτ τον 16ο-17ο αιώνα.

  • Η ανάπτυξη της αναλυτικής γεωμετρίας από τον Ντεκάρτ συσχέτισε τις εξισώσεις α' βαθμού με ευθείες γραμμές, ανοίγοντας νέους δρόμους για την κατανόηση και εφαρμογή τους.

5. Σύγχρονη Εποχή

  • Σήμερα, οι εξισώσεις α' βαθμού είναι θεμέλιο των μαθηματικών, με εφαρμογές σε πολλούς τομείς όπως η φυσική, η οικονομία και η μηχανική. Η συστηματική διδασκαλία τους αποτελεί αναπόσπαστο μέρος της μαθηματικής εκπαίδευσης.

 

ΚΕΦΑΛΑΙΟ 4ο: Ανισώσεις

Ημερολόγιο

Προθεσμία
Γεγονός μαθήματος
Γεγονός συστήματος
Προσωπικό γεγονός

Ανακοινώσεις

Όλες...