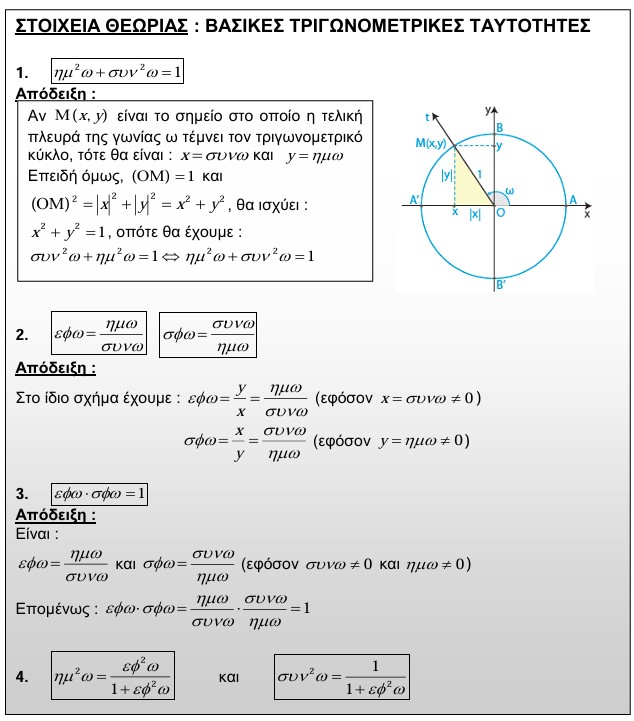
Μάθημα : Μαθηματικά Β' Λυκείου - Αλγεβρα

Η εξίσωση  αx+βy+γ=0, με α,β,γ πραγματικούς αριθμούς και α διαφορο του 0  και ή β διάφορο του 0 , λέγεται γραμμική εξίσωση. Οι μεταβλητές είναι οι άγνωστοι της εξίσωσης αυτής. Οι αριθμοί λέγονται συντελεστές των αγνώστων της εξίσωσης ενώ το λέγεται σταθερός όρος της εξίσωσης.

Όταν ψάχνουμε τις κοινές λύσεις δυο γραμμικών εξισώσεων :

 α x+β y =γ

α΄x+b΄y=γ΄

τότε λέμε ότι έχουμε να λύσουμε γραμμικό σύστημα 2x2 .
Δηλαδή έχω 2 εξισώσεις και 2 αγνώστους. Για να λύσουμε ένα γραμμικό σύστημα 2x2 διαλέγουμε έναν από τους παρακάτω τρόπους. Η επίλυση ενός γραμμικού συστήματος οδηγεί στο αποτέλεσμα είτε : το σύστημα έχει ακριβώς μια λύση, είτε είναι αδύνατο (καμία λύση), είτε είναι αόριστο (άπειρες λύσεις).

Μεθοδολογία 1: ΜΕΘΟΔΟΣ ΑΝΤΙΚΑΤΑΣΤΑΣΗΣ 

ΒΗΜΑ 1 : Διαλέγω μια από τις 2 εξισώσεις, συνήθως αυτή που έχει τουλάχιστον έναν
από τους δυο αγνώστους με συντελεστή 1, και λύνω ως προς τον άγνωστο αυτό.
ΒΗΜΑ 2 : Στη συνέχεια αντικαθιστώ αυτό που βρήκα στην άλλη και έτσι θα έχω
δημιουργήσει μια εξίσωση με έναν μόνο άγνωστο την οποία και λύνω.
ΒΗΜΑ 3 : Αφού βρω τη λύση για τον έναν από τους δυο αγνώστους, αντικαθιστώ την
τιμή του στην άλλη εξίσωση και βρίσκω τον άλλο άγνωστο.

Μεθοδολογία 2: ΜΕΘΟΔΟΣ ΑΝΤΙΘΕΤΩΝ ΣΥΝΤΕΛΕΣΤΩΝ 

ΒΗΜΑ 1 : Δημιουργούμε αντίθετους συντελεστές σε έναν από τους δυο αγνώστους
πολλαπλασιάζοντας με κατάλληλο αριθμό τα μέλη της μιας εξίσωσης ή και των δυο.
ΒΗΜΑ 2 : Προσθέτουμε κατά μέλη τις δυο εξισώσεις, οπότε προκύπτει εξίσωση με έναν
μόνο άγνωστο την οποία και λύνουμε ως προς τον άγνωστο αυτό.
ΒΗΜΑ 3 : Αφού βρω τη λύση για τον έναν από τους δυο αγνώστους, αντικαθιστώ την
τιμή του σε οποία από τις 2 εξισώσεις θέλω και βρίσκω τον άλλο άγνωστο.

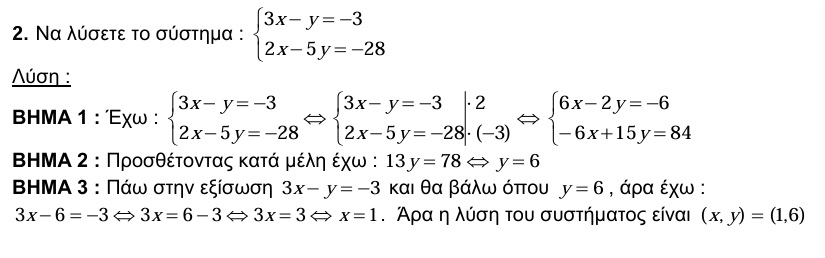
Μεθοδολογία 3: ΜΕΘΟΔΟΣ ΟΡΙΖΟΥΣΩΝ

Για να λύσουμε ένα σύστημα με τη μέθοδο των οριζουσών : βρίσκουμε τις ορίζουσες των D, Dx , Dy και μετά:

ΣΤΟΙΧΕΙΑ ΘΕΩΡΙΑΣ 

ΟΡΙΣΜΟΣ ΣΥΝΑΡΤΗΣΗΣ

Συνάρτηση από ένα σύνολο Α σε ένα σύνολο Β λέγεται μια διαδικασία (κανόνας), με την οποία κάθε στοιχείο του συνόλου Α αντιστοιχίζεται σε ακριβώς ένα στοιχείο του συνόλου Β. Το σύνολο Α λέγεται πεδίο ορισμού της συνάρτησης και περιέχει τις δυνατές τιμές που μπορούμε να δώσουμε στη μεταβλητή x. (το πεδίο ορισμού μιας συνάρτησης f το συμβολίζουμε συνήθως Df . Το σύνολο Β λέγεται σύνολο τιμών της f και περιέχει όλες τις τιμές της  f(x) για τα αντίστοιχα  x ανήκουν στους πραγματικούς αριθμούς.

Ακρότατα Συνάρτησης:

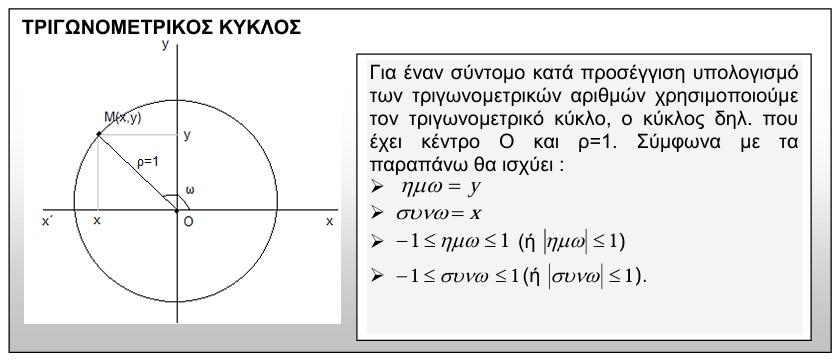
Τριγωνομετρικοί αριθμοί Οξείας Γωνίας (γνωστά από παλαιότερες τάξεις:

Τριγωνομετρικός Κύκλος:

https://www.geogebra.org/m/yD7X579L

Βίντεο:ΑΝΑΓΩΓΗ ΣΤΟ 1o ΤΕΤΑΡΤΗΜΟΡΙΟ - ΤΡΙΓΩΝΟΜΕΤΡΙΑ - ΑΛΓΕΒΡΑ Β΄ΛΥΚΕΙΟΥ

Ο υπολογισμός των τριγωνομετρικών αριθμών οποιασδήποτε γωνίας μπορεί να γίνει, όπως θα δούμε στη συνέχεια, με τη βοήθεια πινάκων που δίνουν τους τριγωνομετρικούς αριθμούς γωνιών από 0^o μέχρι 90^o.

Ας θεωρήσουμε δύο γωνίες ω και ω' που οι τελικές πλευρές τους τέμνουν τον τριγωνομετρικό κύκλο στα σημεία Μ και Μ' αντιστοίχως.

ΓΩΝΙΕΣ ΑΝΤΙΘΕΤΕΣ:

Αν οι γωνίες ω και ω' είναι αντίθετες, δηλαδή αν ω' = −ω, τότε, όπως φαίνεται στο παρακάτω σχήμα, τα σημεία Μ και Μ΄ είναι συμμετρικά ως προς τον άξονα x'x. Επομένως τα σημεία αυτά έχουν την ίδια τετμημένη και αντίθετες τεταγμένες.

Φύλλο Εργασίας: