Μάθημα : Μαθηματικά Β' Λυκείου - Αλγεβρα

Η εξίσωση  αx+βy+γ=0, με α,β,γ πραγματικούς αριθμούς και α διαφορο του 0  και ή β διάφορο του 0 , λέγεται γραμμική εξίσωση. Οι μεταβλητές είναι οι άγνωστοι της εξίσωσης αυτής. Οι αριθμοί λέγονται συντελεστές των αγνώστων της εξίσωσης ενώ το λέγεται σταθερός όρος της εξίσωσης.

Όταν ψάχνουμε τις κοινές λύσεις δυο γραμμικών εξισώσεων :

 α x+β y =γ

α΄x+b΄y=γ΄

τότε λέμε ότι έχουμε να λύσουμε γραμμικό σύστημα 2x2 .
Δηλαδή έχω 2 εξισώσεις και 2 αγνώστους. Για να λύσουμε ένα γραμμικό σύστημα 2x2 διαλέγουμε έναν από τους παρακάτω τρόπους. Η επίλυση ενός γραμμικού συστήματος οδηγεί στο αποτέλεσμα είτε : το σύστημα έχει ακριβώς μια λύση, είτε είναι αδύνατο (καμία λύση), είτε είναι αόριστο (άπειρες λύσεις).

Μεθοδολογία 1: ΜΕΘΟΔΟΣ ΑΝΤΙΚΑΤΑΣΤΑΣΗΣ 

ΒΗΜΑ 1 : Διαλέγω μια από τις 2 εξισώσεις, συνήθως αυτή που έχει τουλάχιστον έναν
από τους δυο αγνώστους με συντελεστή 1, και λύνω ως προς τον άγνωστο αυτό.
ΒΗΜΑ 2 : Στη συνέχεια αντικαθιστώ αυτό που βρήκα στην άλλη και έτσι θα έχω
δημιουργήσει μια εξίσωση με έναν μόνο άγνωστο την οποία και λύνω.
ΒΗΜΑ 3 : Αφού βρω τη λύση για τον έναν από τους δυο αγνώστους, αντικαθιστώ την
τιμή του στην άλλη εξίσωση και βρίσκω τον άλλο άγνωστο.

Μεθοδολογία 2: ΜΕΘΟΔΟΣ ΑΝΤΙΘΕΤΩΝ ΣΥΝΤΕΛΕΣΤΩΝ 

ΒΗΜΑ 1 : Δημιουργούμε αντίθετους συντελεστές σε έναν από τους δυο αγνώστους
πολλαπλασιάζοντας με κατάλληλο αριθμό τα μέλη της μιας εξίσωσης ή και των δυο.
ΒΗΜΑ 2 : Προσθέτουμε κατά μέλη τις δυο εξισώσεις, οπότε προκύπτει εξίσωση με έναν
μόνο άγνωστο την οποία και λύνουμε ως προς τον άγνωστο αυτό.
ΒΗΜΑ 3 : Αφού βρω τη λύση για τον έναν από τους δυο αγνώστους, αντικαθιστώ την
τιμή του σε οποία από τις 2 εξισώσεις θέλω και βρίσκω τον άλλο άγνωστο.

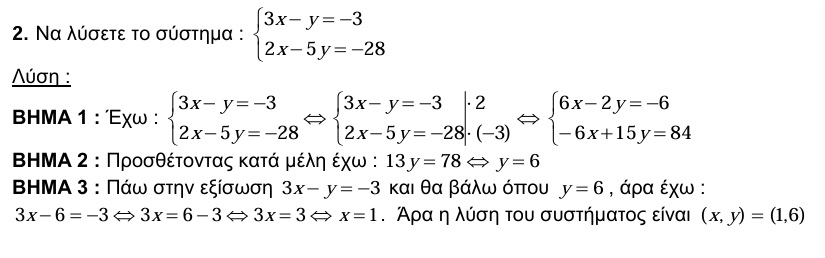
Μεθοδολογία 3: ΜΕΘΟΔΟΣ ΟΡΙΖΟΥΣΩΝ

Για να λύσουμε ένα σύστημα με τη μέθοδο των οριζουσών : βρίσκουμε τις ορίζουσες των D, Dx , Dy και μετά: