Μάθημα : Μαθηματικά Β' Γυμνασίου - Γεωμετρία
Κωδικός : 5204021226
5204021226 - ΔΙΟΝΥΣΙΟΣ ΟΙΚΟΝΟΜΟΥ
Περιγραφή Μαθήματος

Το παρόν μάθημα στο eclass δημιουργήθηκε για να διευκολύνει τη συνεργασία του εκπαιδευτικού με τους μαθητές της Β' Γυμνασίου του Γυμνασίου Αγκιστρίου με ΛΤ.
- Εμβαδόν τετραγώνου
Το εμβαδόν ενός τετραγώνου πλευράς α ισούται με α2
- Εμβαδόν ορθογωνίου
Το εμβαδόν ενός ορθογωνίου με πλευρές α, β ισούται με α β
Εμβαδόν ορθογωνίου και τετραγώνου - YouTube
- Εμβαδόν παραλληλογράμμου
Το εμβαδόν ενός παραλληλογράμμου είναι ίσο με το γινόμενο μίας βάσης του με το αντίστοιχο ύψος.
Εμβαδόν παραλληλογράμμου - YouTube
- Εμβαδόν τυχαίου τριγώνου
- Εμβαδόν ορθογωνίου τριγώνου
Το εμβαδόν ενός ορθογωνίου τριγώνου είναι ίσο με το μισό του γινομένου των δύο κάθετων πλευρών του
- Εμβαδόν τραπεζίου
To εμβαδόν ενός τραπεζίου είναι ίσο με το γινόμενο του ημιαθροίσματος των βάσεών του με το ύψος του.
Στον παρακάτω σύνδεσμο θα βρείτε μια ενδιαφέρουσα εφαρμογή για την κατανόηση των τύπων των βασικών σχημάτων.
http://photodentro.edu.gr/v/item/ds/8521/5771
επιλέγετε πρώτα το τετράγωνο και μετακινώντας τον δρομέα αυξομειώνετε τις διαστάσεις του υπολογίζοντας το εμβαδόν του. Ιδιαίτερο ενδιαφέρον παρουσιάζουν τα εμβαδά παραλληλογράμμου, τριγώνου, τραπεζίου.
Στους παρακάτω σύνδεσμους θα βρείτε quiz ερωτήσεων για την κατανόηση των τύπων των βασικών σχημάτων.
Περίμετρος και εμβαδόν - Άνοιξε το κουτί
Εμβαδά επίπεδων σχημάτων. Ταίριαξε το κάθε σχήμα με το όνομα και το εμβαδόν του.
ΠΥΘΑΓΟΡΕΙΟ ΘΕΩΡΗΜΑ:
Το τετράγωνο της υποτείνουσας οποιουδήποτε ορθογωνίου τριγώνου είναι ίσο με το άθροισμα των τετραγώνων των δύο κάθετων πλευρών του. Δηλαδή,
![]()
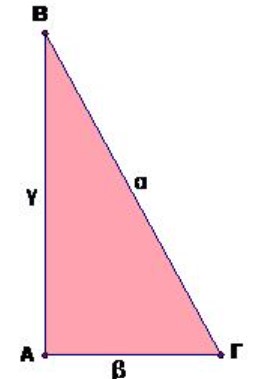
Το θεώρημα αναφέρεται σε μια σχέση που ισχύει σε κάθε ορθογώνιο τρίγωνο. Και πιο συγκεκριμένα η σχέση αυτή μας πληροφορεί για το τι συμβαίνει με τα μήκη των πλευρών του. Με αυτή την ισότητα που μας δίνει το θεώρημα, μπορούμε να υπολογίσουμε μια πλευρά του αρκεί να γνωρίζουμε το μήκος των άλλων δύο πλευρών.
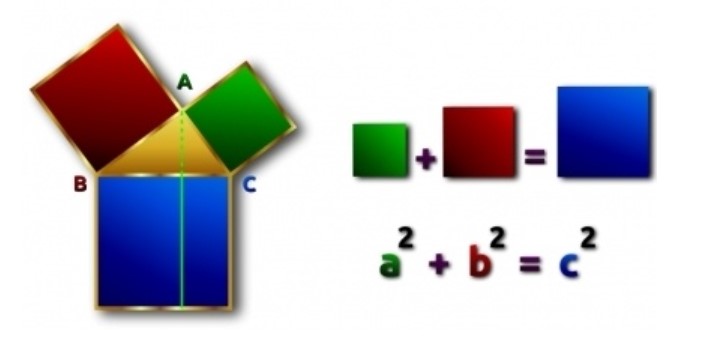
Το θεώρημα έχει μεγάλο αριθμό αποδείξεων, πιθανότατα μεγαλύτερο από κάθε άλλο μαθηματικό θεώρημα. Οι αποδείξεις είναι ευθείες και το σύνολο τους συμπεριλαμβάνει τόσο γεωμετρικές όσο και αλγεβρικές αποδείξεις, κάποιες από της οποίες χρονολογούνται αρκετές χιλιετίες πριν.
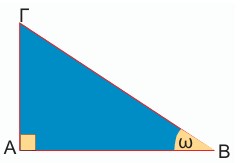
Σε οποιοδήποτε ορθογώνιο τρίγωνο με οξεία γωνία ω ο σταθερός αυτός λόγος γράφεται ως εξής:
![]()
ονομάζεται εφαπτομένη της γωνίας ω και συμβολίζεται με εφω.
Ημερολόγιο
Ανακοινώσεις
Όλες...- - Δεν υπάρχουν ανακοινώσεις -