Μάθημα : Άλγεβρα Α Τάξης

Γεια σας παιδιά,

Με τη βοήθεια των συντεταγμένων σημείων στο επίπεδο, δίνεται η δυνατότητα, να χαράξουμε, για μια συνάρτηση, τη γραφική της παράσταση. Αυτό πραγματοποιείται, με τη βοήθεια της συμπλήρωσης ενός πίνακα τιμών της συνάρτησης. Για να καταλάβετε, καλύτερα, τη διαδικασία της χάραξης της γραφικής παράστασης, καθώς και τους συμβολισμούς όπως και τις έννοιες αυτής της ενότητας, θα ήθελα να σας προτείνω  να ασχοληθείτε, αρχικά, με την παρακάτω διαδραστική δοκιμασία.

Συναρτήσεις (Γραφική παράσταση συνάρτησης)

Βέβαια, υπάρχουν και πιο σύνθετα ερωτήματα που μπορούν να μας απασχολήσουν όταν οι συναρτήσεις παριστάνονται γραφικά. Μπορεί να χρειάζεται να προσδιορίσουμε ορισμένα χαρακτηριστικά σημεία των γραφημάτων όπως είναι τα σημεία τομής τους με τους άξονες συντεταγμένων. Επίσης, κάποιες φορές ενδιαφερόμαστε να προσδιορίσουμε πότε (δηλαδή, για ποια \(x)\) το γράφημα μιας συνάρτησης τέμνει (συναντά) το γράφημα μιας άλλης συνάρτησης ή πότε (δηλαδή, για ποια \(x)\) ένα γράφημα βρίσκεται πάνω / κάτω από κάποιο άλλο γράφημα.

Για παράδειγμα, η συνάρτηση, \(y = x^2 -5x+6\), έχει την ακόλουθη γραφική παράσταση:

Να παρατηρήσετε ότι οι τετμημένες των σημείων τομής, \(A\) και \(B\), της προηγούμενης γραφικής παράστασης, με τον οριζόντιο άξονα \(x'x\), είναι οι αριθμοί \(2\) και \(3\). Αλγεβρικά, οι αριθμοί αυτοί προκύπτουν από την επίλυση της εξίσωσης \(x^2-5x+6=0\) αφού ένα σημείο του άξονα \(x'x\) έχει τεταγμένη \(y\) ίση με το \(0\). Εδώ, ειδικότερα, εφόσον το σημείο πρέπει να βρίσκεται και στη γραφική παράσταση της συγκεκριμένης συνάρτησης, είναι \(y=x^2-5x+6\). Έτσι, \(x^2-5x+6=0\Leftrightarrow x=2 \textrm{ ή } x=3\).

Ακόμη, το τριώνυμο \(f(x) = x^2 +x+1\), δεν έχει ρίζες αφού η διακρίνουσα του είναι αρνητική. Να παρατηρήσετε τη γραφική του παράσταση:

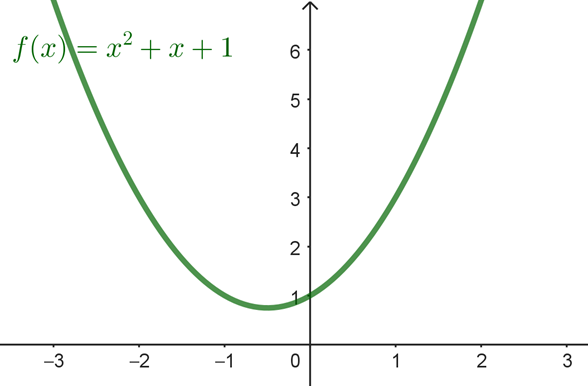
Έτσι, λοιπόν, η εξίσωση \(y=0\) (ή αλλιώς \(f(x)=0\)) δε δίνει λύση (αδύνατη), άρα δεν υπάρχουν σημεία του γραφήματος με \(y=0\), δηλαδή, σημεία του γραφήματος που βρίσκονται συγχρόνως στον οριζόντιο άξονα. Μάλιστα, όπως παρατηρείτε, το τριώνυμο είναι πάνω από τον οριζόντιο άξονα δηλαδή – το \(y\) – είναι θετικό. (Λογικό αφού η διακρίνουσα του είναι αρνητική οπότε είναι ομόσημο του \(\alpha=1>0\). )

Για να βρούμε για ποια \(x\) το τριώνυμο αυτό είναι κάτω από την ευθεία \(y=2x+3\) πρέπει να λύσουμε την ανίσωση: \(x^2 +x+1<2x+3\). (Ανίσωση β΄βαθμού --> Όλα στο α΄μέλος --> Πίνακας προσήμου --> Λύσεις). Να το δείτε και γραφικά:

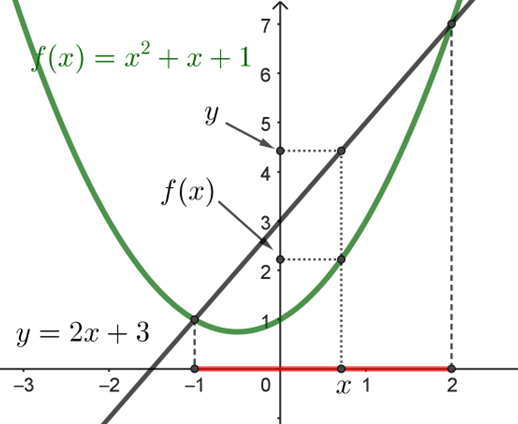
Το \(y\) ή \(f(x)\) της συνάρτησης \(f\) πρέπει να είναι κάτω (μικρότερο) από το αντίστοιχο \(y\) (δηλαδή το \(2x+3\)) της ευθείας. Αυτό συμβαίνει όταν \(-1<x<2\) ή όταν \(x\in(-1,2)\).

Για να ξεδιαλύνετε τα προηγούμενα ζητήματα, θα μπορούσατε να δοκιμάσετε να απαντήσετε στα ερωτήματα της παρακάτω διαδραστικής δοκιμασίας.

Συναρτήσεις (Γραφική παράσταση συνάρτησης - Σημεία τομής με τους άξονες - Σχετικές θέσεις γραφημάτων)

Χαιρετώ σας!