Μάθημα : ΦΥΣΙΚΗ ΘΕΤΙΚΟΥ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ Β ΛΥΚΕΙΟΥ

Ένα μικρό σώμα μάζας 0,2kg αφήνεται στη θέση Α, να ολισθήσει κατά μήκος ενός λείου κεκλιμένου επιπέδου κλίσεως θ, όπου ημθ=0,6 και συνθ=0,8. Φτάνοντας στο σημείο Β, σε κατακόρυφη απόσταση h=1,25m, συναντά μια λεία κυκλική τροχιά, κέντρου Ο και ακτίνας R=0,5m στην οποία συνεχίζει την κίνησή του. Η ακτίνα ΟΒ είναι κάθετη στο κεκλιμένο επίπεδο.

• 
• Ένα μικρό σώμα μάζας 0,2kg ηρεμεί σε λείο οριζόντιο επίπεδο. Δένουμε το σώμα με ένα αβαρές οριζόντιο νήμα μήκους L, στο άλλο άκρο του οποίου ασκούμε μια σταθερή οριζόντια δύναμη μέτρου F=0,4Ν, τραβώντας το σώμα, τη στιγμή t₀=0. Τη χρονική στιγμή t₁=4s, παύουμε να τραβάμε το νήμα, το ελεύθερο άκρο του οποίου στερεώνουμε σε σταθερό σημείο Ο του οριζοντίου επιπέδου τη στιγμή t₂=5s, σε τέτοια θέση, έτσι ώστε το νήμα να είναι κάθετο στην ταχύτητα του σώματος, όπως στο σχήμα, οπότε το σώμα συνεχίζει να κινείται σε οριζόντια κυκλική τροχιά ακτίνας L. Αν η τάση του νήματος στη διάρκεια της κυκλικής κίνησης είναι δεκαπλάσια της τάσης κατά την ευθύγραμμη κίνηση, να βρεθούν:

Από την κορυφή λείου κεκλιμένου επιπέδου αφήνουμε σώμα το οποίο όταν φτάνει στην βάση του εισέρχεται στο λείο ημικύκλιο του σχήματος. Στο ανώτερο σημείο Α η δύναμη που δέχεται το σώμα από το ημικύκλιο έχει μέτρο F_A = 3mg, όπου m η μάζα του σώματος. Από το σημείο Α και μετά το σώμα εκτελεί οριζόντια βολή και την στιγμή που συγκρούεται με το κεκλιμένο επίπεδο η ταχύτητά του είναι κάθετη σε αυτό.

Το ημικύκλιο έχει ακτίνα R η οποία να θεωρηθεί γνωστή και η γωνία του κεκλιμένου επιπέδου είναι φ = 60⁰, επίσης η επιτάχυνση της βαρύτητας είναι g.

Δίνεται ημ60^ο=√3/2, συν 60^ο=1/2, εφ60^ο=√3

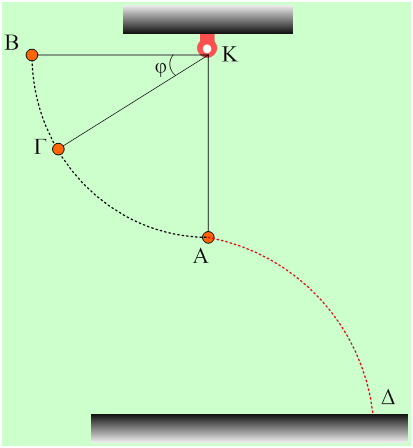
Μια μικρή σφαίρα μάζας 0,2kg ηρεμεί στο κάτω άκρο νήματος μήκους ℓ=1,25m (θέση Α), το άλλο άκρο του οποίου είναι δεμένο σε σταθερό σημείο Κ, το οποίο βρίσκεται σε ύψους Η=2,5m από το έδαφος.

Φέρνουμε τη σφαίρα στη θέση Β, ώστε το νήμα να γίνει  οριζόντιο και την αφήνουμε να κινηθεί. Τη στιγμή που το νήμα γίνεται κατακόρυφο κόβεται, οπότε τελικά η σφαίρα φτάνει στο έδαφος στο σημείο Δ.

Δίνεται g=10m/s², ενώ η αντίσταση του αέρα θεωρείται αμελητέα.

ΠΗΓΗ

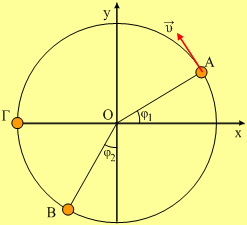
Μια μικρή σφαίρα, μάζας 2kg, εκτελεί ομαλή κυκλική κίνηση, σε κύκλο κέντρου Ο και ακτίνας 0,5m, όπως στο σχήμα. Τη χρονική στιγμή t=0 η σφαίρα περνά από τη θέση Α, ενώ φτάνει για πρώτη φορά στη θέση Β τη χρονική στιγμή t₁=0,35s, όπου οι σημειωμένες γωνίες είναι φ₁=φ₂= 30°.

Δίνεται g=10m/s².ΠΗΓΗ

Ένα ξύλινο σώ­μα Σ μά­ζας  Μ=950g κρέ­με­ται α­πό νή­μα μή­κους 2,5m. Ένα βή­μα μά­ζας m=50g που κι­νεί­ται ο­ρι­ζό­ντια με τα­χύ­τη­τα υ₁= 100m/s σφη­νώ­νε­ται στο Σ.

Δίνεται g=10m/s².

ΠΗΓΗ

Αεροπλάνο κινείται οριζόντια με ταχύτητα υ₁=100m/s και σε ύψος 105m από το έδαφος. Στο έδαφος κινείται αντίρροπα όχημα με ταχύτητα μέτρου υ₂, στην ίδια διεύθυνση κίνησης με το αεροπλάνο. Όταν το αεροπλάνο απέχει από το όχημα οριζόντια απόσταση s=548.6m, αφήνεται μία βόμβα. Η βόμβα αστοχεί γιατί το όχημα έχει προσπεράσει το σημείο επαφής της βόμβας με το έδαφοςκατά χ=1m. Αν η αντίσταση του αέρα θεωρείται αμελητέα και η επιτάχυνση της βαρύτητας είναι g=10m/s²,να υπολογίσετε:

Αν η ταχύτητα του αέρα θεωρείται αμελητέα και η επιτάχυνση της βαρύτητας είναι g=10m/s^2

Ανοίξτε το αρχείο της προσομοίωσης «Οριζόντια Βολή» του συναδέλφου Ηλία Σιτσανλή, που υπάρχει στο μενού «έγγραφα»

Θεωρούμε ότι η αρχική θέση του σώματος βρίσκεται σε ύψος H=20m από το έδαφος. Θέστε στο ύψος την τιμή των 20m.
ΠΗΓΗ

Ανοίξετε την προσομοίωση του Ηλία Σιτσανλή

Στις παρακάτω ερωτήσεις σας δίνονται οι τιμές των γωνιακών ταχυτήτων εκάστου κινητού. Σε κάθε περίπτωση να βάλετε στην προσομοίωση τις τιμές αυτές και να δείτε το χρόνο της πρώτης και δεύτερης συνάντησης των κινητών. Δείτε επίσης τα διαστήματα που διαγράφουν τα κινητά σε κάθε περίπτωση. Στη συνέχεια σας ζητείται να υπολογίσετε με τους τύπους που γνωρίζετε στην ΟΚΚ τα μεγέθη αυτά.